MCMC using Markov bases for computing $p$-values in decomposable log-linear models

Abstract

We derive an explicit form of a Markov basis on the junction tree for a decomposable log-linear model. Then we give a description of a Markov basis characterized by global Markov properties associated with the graph of a decomposable log-linear model and show how to use the Markov basis for generating contingency tables of a Markov chain. The estimates of exact $p$-values can be obtained from contingency tables generated from the proposed Markov chain Monte Carlo using the Markov basis.

Appendix: Configuration \(A\) of the conditional independence model for a three-way contingency table

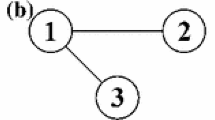
We consider a $2 \times 2 \times 3$ table cross-classified by $X=(X_{1},X_{2},X_{3})$. For the table, we assume the conditional independence that $X_{1} \perp X_{2} | X_{3}$. When we consider the reverse lexicographic order of the cell indices in $\{1,2\} \times \{1,2\} \times \{1,2,3\}$, that is, $(1,1,1),(2,1,1),\ldots ,(2,2,3)$, $A$ for the conditional independence model is given by

$$\begin{aligned} A=\left(\begin{array}{c} E_{3} \otimes \mathbf 1 _{2}^{\top } \otimes E_{1} \\ E_{3} \otimes E_{2} \otimes \mathbf 1 _{1}^{\top } \end{array} \right) =\left(\begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 1&0&1&0&&0&0&0&0&&0&0&0&0 \\ 0&1&0&1&&0&0&0&0&&0&0&0&0 \\ 0&0&0&0&&1&0&1&0&&0&0&0&0 \\ 0&0&0&0&&0&1&0&1&&0&0&0&0 \\ 0&0&0&0&&0&0&0&0&&1&0&1&0 \\ 0&0&0&0&&0&0&0&0&&0&1&0&1 \\ 1&1&0&0&&0&0&0&0&&0&0&0&0 \\ 0&0&1&1&&0&0&0&0&&0&0&0&0 \\ 0&0&0&0&&1&1&0&0&&0&0&0&0 \\ 0&0&0&0&&0&0&1&1&&0&0&0&0 \\ 0&0&0&0&&0&0&0&0&&1&1&0&0 \\ 0&0&0&0&&0&0&0&0&&0&0&1&1 \\ \end{array} \right). \end{aligned}$$

By permuting rows of A, we have the block diagonal matrix

$$\begin{aligned} A^{\prime } =\left(\begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 1&0&1&0&&0&0&0&0&&0&0&0&0 \\ 0&1&0&1&&0&0&0&0&&0&0&0&0 \\ 1&1&0&0&&0&0&0&0&&0&0&0&0 \\ 0&0&1&1&&0&0&0&0&&0&0&0&0 \\ \hline 0&0&0&0&&1&0&1&0&&0&0&0&0 \\ 0&0&0&0&&0&1&0&1&&0&0&0&0 \\ 0&0&0&0&&1&1&0&0&&0&0&0&0 \\ 0&0&0&0&&0&0&1&1&&0&0&0&0 \\ \hline 0&0&0&0&&0&0&0&0&&1&0&1&0 \\ 0&0&0&0&&0&0&0&0&&0&1&0&1 \\ 0&0&0&0&&0&0&0&0&&1&1&0&0 \\ 0&0&0&0&&0&0&0&0&&0&0&1&1 \\ \end{array} \right) = \left( \begin{array}{ccc} A_{22}&&0\\&A_{22}&\\ 0&&A_{22} \end{array} \right) = \left( \begin{array}{c} A_{1}^{\prime } \\ A_{2}^{\prime } \\ A_{3}^{\prime } \\ \end{array} \right). \end{aligned}$$