A partitioned quasi-likelihood for distributed statistical inference

Abstract

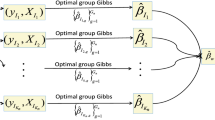
In the big data setting, working data sets are often distributed on multiple machines. However, classical statistical methods are often developed to solve the problems of single estimation or inference. We employ a novel parallel quasi-likelihood method in generalized linear models, to make the variances between different sub-estimators relatively similar. Estimates are obtained from projection subsets of data and later combined by suitably-chosen unknown weights. We also show the proposed method to produce better asymptotic efficiency than using the simple average. Furthermore, simulation examples show that the proposed method can significantly improve statistical inference.

Appendix

Proof of Theorem 1:

We first prove the existence of the sequence $\{w^{opt}_{n,g}\}_{g=1}^{G_n}$. Note that

$$\begin{aligned} \text {var}(\hat{\beta }_A)=\frac{1}{G_{n}^2}\sum _{g=1}^{G_n} \text {var}(\hat{\beta }_{n,g}),\ \text {var}(\hat{\beta }_w)= \sum _{g=1}^{G_n} w_{n,g}^2\text {var}(\hat{\beta }_{n,g}). \end{aligned}$$

And

$$\begin{aligned} \text {tr(var}(\hat{\beta }_A))=\frac{1}{G_{n}^2}\sum _{g=1}^{G_n} \text {tr(var}(\hat{\beta }_{n,g})), \ \text {tr(var}(\hat{\beta }_w))= \sum _{g=1}^{G_n} w_{n,g}^2\text {tr(var}(\hat{\beta }_{n,g})). \end{aligned}$$

Let

$$\begin{aligned} \text {tr}_{1}=\min \{\text {tr}(\text {var}(\hat{\beta }_{n,g}))\},\ldots , \text {tr}_{G_n}=\max \{\text {tr}(\text {var}(\hat{\beta }_{n,g}))\}. \end{aligned}$$

Then

$$\begin{aligned} \text {tr(var}(\hat{\beta }_A))=\sum _{g=1}^{G_n}\text {tr}_g/G_n^2,\ \text {tr(var}(\hat{\beta }_w))=\sum _{g=1}^{G_n}w_{n,g}^2\text {tr}_g. \end{aligned}$$

(i) For $m\in \mathbb {N}^+$, $G_n=2m+1$. We set $w_{n,1}+w_{n,2m+1}=\ldots =w_{n,m}+w_{n,m+2}=2/G_n$ and $w_{n,m+1}=1/G_n$. Let $w_{n,1} =\ldots =w_{n,m} >1/G_n$, we have $\text {tr(var}(\hat{\beta }_w))\le \text {tr(var}(\hat{\beta }_A))$.

If we set $w_{n,1}+w_{n,2}+w_{n,2m}+w_{n,2m+1}=\ldots =w_{n,m-1}+w_{n,m} +w_{n,m+2} +w_{n,m+3}=4/G_n$, $w_{n,m+1}=1/G$. Let $w_{n,1}+w_{n,2}=\ldots =w_{n,m-1}+w_{n,m}>2/G_n$, we have $\text {tr(var}(\hat{\beta }_w))\le \text {tr(var}(\hat{\beta }_A))$.

If we set $w_{n,1}+w_{n,2}+w_{n,3}+w_{n,2m-1}+w_{n,2m}+w_{n,2m+1}=\ldots =w_{n,m-2}+w_{n,m-1}+w_{n,m} +w_{n,m+2} +w_{n,m+3}+w_{n,m+4}=6/G_n$, $w_{n,m+1}=1/G_n$. Let $w_{n,1}+w_{n,2}+w_{n,3}=\ldots =w_{n,m-2}+w_{n,m-1}+w_{n,m}>3/G_n$, we have $\text {tr(var}(\hat{\beta }_w))\le \text {tr(var}(\hat{\beta }_A))$.

(ii) For $m\in \mathbb {N}^+$ with $G_n=2m$. We set $w_{n,1}+w_{n,2m}=\ldots =w_{n,m}+w_{n,m+1}=2/G_n$. Let $w_{n,1} =\ldots =w_{n,m} >1/G_n$,

If we set $w_{n,1}+w_{n,2}+w_{n,2m-1}+w_{n,2m}=\ldots =w_{n,m-1}+w_{n,m}+w_{n,m+1}+w_{n,m+2}=4/G_n$ when m is even number. Let $w_{n,1}+w_{n,2}=\ldots =w_{n,m-1}+w_{n,m}>2/G_n$, we have $\text {tr(var}(\hat{\beta }_w))\le \text {tr(var}(\hat{\beta }_A))$.

We now derive the optimal weight sequence $\{w^{opt}_{n,g}\}_{g=1}^{G_n}$ for $\hat{\beta }_w$. We choose Lagrangian multiplier method to prove the theorem. We set $v_g=\text {tr(var}(\hat{\beta }_{n,g}))$ and objective function

$$\begin{aligned} l(w,\lambda )=\sum _{g=1}^{G_{n}} w_{n,g}^2 v_g+\lambda \Big (\sum _{g=1}^{G_{n}} w_{n,g}-1\Big ), \end{aligned}$$

where $\lambda$ is a Lagrangian multiplier parameter. Taking the derivative of $l(w,\lambda )$ gives

$$\begin{aligned} \frac{\partial l(w,\lambda )}{\partial w_{n,g} }=2w_{n,g}v_g+\lambda ,\ g=1,\ldots ,G_n. \end{aligned}$$

And

$$\begin{aligned} w_{n,g}v_g=-\frac{1}{2}\cdot \lambda v_g^{-1}, \sum _{g=1}^{G_{n}} w_{n,g}=-\lambda \cdot \sum _{g=1}^{G_{n}}v_g^{-1}/2=1. \end{aligned}$$

We then have optimal weight

$$\begin{aligned} w^{opt}_{n,g}=v_g^{-1}\Big /\sum _{g=1}^{G_{n}}v_g^{-1}, \ g=1,\ldots ,G_n. \end{aligned}$$

We also obtain $\text {tr(var}(\hat{\beta }_{w^{opt}}))=1/\sum _{g=1}^{G_{n}} v_g^{-1}$. $\Box$

Proof of Theorem 2:

Observing that $e^x\le 1+x+\frac{1}{2}x^2e^{|x|}$ ($x>0$), we obtain

$$\begin{aligned} \sum _{n=1}^\infty n^{r-2} P\Big (\sum _{g=1}^{G_n}w_{n,g}\Vert \varepsilon _{n,g}\Vert _1>\epsilon \Big )\le & {} \sum _{n=1}^\infty n^{r-2} e^{-\epsilon t} E\exp \Big \{t\sum _{g=1}^{G_n}w_{n,g}\Vert \varepsilon _{n,g}\Vert _1\Big \}\ (t=M\log n/\epsilon ) \\\le & {} \sum _{n=1}^\infty n^{r-2-M} \prod _{g=1}^{G_n} E\exp \{t w_{n,g}\Vert \varepsilon _{n,g}\Vert _1\} \\\le & {} \sum _{n=1}^\infty n^{r-2-M} \prod _{g=1}^{G_n} \Big [1+\frac{1}{2}t^2w_{n,g}^2E\varepsilon _{n,g}^2 e^{t w_{ng}\Vert \varepsilon _{n,g}\Vert _1}\Big ] \\\le & {} \sum _{n=1}^\infty n^{r-2-M} \prod _{g=1}^{G_n} \Big [1+c(\log n)^2 w_{n,g}^2E \exp \{(1+c)\Vert \varepsilon _{n,g}\Vert _1\}\Big ] \\\le & {} \sum _{n=1}^\infty n^{r-2-M} \exp \Big \{ c(\log n)^2 \sum _{g=1}^{G_n} w_{n,g}^2 \Big \} \\\le & {} \sum _{n=1}^\infty n^{r-2-M+\epsilon } < \infty ,\epsilon >0. \end{aligned}$$

Here M is a large constant such that $M>(r+\epsilon )$, c is a suitable constant. Thus we have the theorem. $\Box$

Proof of Theorem 3:

We get this proof through the characteristic function method. For $1\le u\le G_n-1$,

$$\begin{aligned} \sum _{g,h=1,|g-h|\ge u}^{G_n}\Vert |w_{n,g}w_{n,h}\text {cov}(\varepsilon _{n,g},\varepsilon _{n,h})\Vert |\le \sup _k\bigg \Vert \bigg |\sum _{h=1,|k-h|\ge u}^{G_n}\text {cov}(\varepsilon _{n,g},\varepsilon _{n,h})\bigg |\bigg \Vert \Big (\sum _{g=1}^{G_n} w_{n,g}^2\Big ). \end{aligned}$$

By Eqs. (3.3) and (3.4), for any $\epsilon >0$, there exists $u=u_\epsilon$ satisfying

$$\begin{aligned} 0\le \sum _{g,h=1,|g-h|\ge u}^{G_n} w_{n,g}w_{n,h}\Vert |\text {cov}(\varepsilon _{n,g},\varepsilon _{n,h})\Vert |\le \epsilon . \end{aligned}$$

Define

$$\begin{aligned} K=\Big [\frac{1}{\epsilon }\Big ], Y_{n,g}=\sum _{h=ug+1}^{u(g+1)}w_{n,h} \varepsilon _{n,h},\ g=0,1,2,\ldots . \end{aligned}$$

$$\begin{aligned} A_h=\Big \{g: 2Kh \le g\le 2Kh+K,\Vert |\text {cov}(Y_{n,g},Y_{n,g+1}) \Vert |\le \frac{1}{K}\Vert |\sum _{g=2Kh}^{2Kh+K}\text {var}(Y_{n,g})\Vert |\Big \}. \end{aligned}$$

Due to $2\Vert |\text {cov}(Y_{n,g},Y_{n,g+1})\Vert |\le \Vert |\text {var}(Y_{n,g})\Vert |+\Vert |\text {var}(Y_{n,g+1})\Vert |$, $A_h$ is nonempty for any h. Let $m_0=0$, $m_{h+1}=\min \{m:m>m_h,m\in A_h\}$ for $\{m_g\}_{g=1}^{G_n}$, and set

$$\begin{aligned} Z_{n,h}=\sum _{g=m_h+1}^{m_h+1}Y_{n,g}(h=0,1,2,\ldots ). \ \Delta _h=\{u(m_h+1)+1,\ldots ,u(m_{h+1}+1)\}. \end{aligned}$$

Note that

$$\begin{aligned} Z_{n,h}=\sum _{k\in \Delta _h}w_{n,k}\varepsilon _{n,k},\ h=0,1,\ldots ,G_n. \end{aligned}$$

For any t,

$$\begin{aligned}&\bigg |E\exp \Big (it\sum _{h=1}^{G_n}\Vert Z_{n,h}\Vert _1\Big )-\prod _{h=1}^{G_n} E\exp (it\Vert Z_{n,h}\Vert _1)\bigg | \\&\quad \le \Big |\text {cov}\Big (\exp \big (it\sum _{h=1}^{G_n-1}\Vert Z_{n,h}\Vert _1\big ),\exp (it \Vert Z_{n,G_n})\Vert _1\big )\Big | \\&\qquad +|E\exp (it \Vert Z_{n,h}\Vert _1)|\Big |E\exp \big (it\sum _{h=1}^{G_n-1}\Vert Z_{n,h}\Vert _1\big )-\prod _{h=1}^{G_n-1} E\exp (it\Vert Z_{n,h}\Vert _1)\Big | \\&\quad \ll t^2\cdot \sum _{1\le g<h\le G_n} \text {cov}(\Vert Z_{n,g}\Vert _1,\Vert Z_{n,h}\Vert _1) \\&\quad = t^2\cdot \bigg [\sum _{1\le g<h\le G_n,|g-h|=1} \text {cov}(\Vert Z_{n,g}\Vert _1,\Vert Z_{n,h}\Vert _1) +\sum _{1\le g<h\le G_n,|g-h|>1} \text {cov}(\Vert Z_{n,g}\Vert _1,\Vert Z_{n,h}\Vert _1) \bigg ] \\&\quad \ll t^2\cdot \bigg [\sum _{1\le g<h\le G_n,|g-h|\ge u} w_{n,g}w_{n,h} \text {cov}(\Vert \varepsilon _{n,g}\Vert _1,\Vert \varepsilon _{n,h}\Vert _1) \bigg ] \\&\qquad + \sum _{h=1}^{G_n} \text {cov}(\Vert Y_{n,h}\Vert _1,\Vert Y_{n,h+1}\Vert _1) \\&\quad \ll t^2 \cdot \Big [\varepsilon +\frac{O(1)}{K}\sum _{g=1}^{G_n}\text {var}(\Vert Y_{n,g}\Vert _1)\Big ]\ll \epsilon t^2. \end{aligned}$$

We then have the theorem. $\Box$

Proof of Theorem 4:

We first show that $\sqrt{n}(\hat{\beta }_w-\beta ^*)$ is bounded when $G_n=O(p_n)$, after we present two lemmas of Huang and Huo (2015),

$$\begin{aligned} E[\Vert \sqrt{p_n}(\hat{\beta }_{n,g}-\beta ^*)\Vert ^2]\le & {} 2 \text {tr}\{\Sigma \} +O(p_n^{-1})\ \text {from}\ \text {Lemma} \ \text {B.1}, \end{aligned}$$

(7.1)

$$\begin{aligned} \Vert E\sqrt{p_n}(\hat{\beta }_w-\beta ^*)\Vert \le O(1/\sqrt{p_n})\ \text {from}\ \text {Lemma} \ \text {B.5}. \end{aligned}$$

(7.2)

By applying Theorem 3 and (7.1), we have

$$\begin{aligned} \sqrt{n} (\hat{\beta }_w-\beta ^*)= & {} \frac{1}{\sqrt{G_n}}\sum _{g=1} \bigg \{w_{n,g}\sqrt{p_n}(\hat{\beta }_{n,g}-\beta ^*) - E[w_{n,g}\sqrt{p_n}(\hat{\beta }_{n,g}-\beta ^*)] \bigg \}\\&+\sqrt{n}E(\hat{\beta }_{n,1}-\beta ^*)\\&{\mathop {\longrightarrow }\limits ^{d}} N(0,\Sigma )+\lim _{n\rightarrow \infty } \sqrt{n}E(\hat{\beta }_{n,1}-\beta ^*). \end{aligned}$$

Then $\lim _{n\rightarrow \infty } \sqrt{n} E (\hat{\beta }_{n,1}-\beta ^*)$ is finite. By (7.2), we have $\Vert E(\hat{\beta }_{n,g}-\beta ^*)\Vert =O(1/p_n),\ g=1,2,\ldots ,G_n$. Thus

$$\begin{aligned} \Vert \sqrt{n} (\hat{\beta }_{n,g}-\beta ^*)\Vert =O(1)\ \text {if} \ G_n=O(p_n), \end{aligned}$$

and when $G_n=O(p_n)$, $\sqrt{n} \Vert \hat{\beta }_w-\beta ^*\Vert =O(1)\ \text {as} \ n \rightarrow \infty$.

By Theorem 4.2 of Lang (1993), there exists an integrator variable $\rho \ (\in [0,1])$ such that

$$\begin{aligned}&\frac{\sqrt{n}}{a}\cdot F(\hat{\beta }_w)(\tilde{\beta }_w-\beta ^*)\\&\quad = F(\hat{\beta }_w)\cdot \sqrt{n}(\hat{\beta }_w-\beta ^*)-\sqrt{n}(s(\hat{\beta }_w)-s(\beta ^*))-\sqrt{n}s(\beta ^*) \\&\quad = F(\hat{\beta }_w)\cdot \sqrt{n}(\hat{\beta }_w-\beta ^*)-\sqrt{n}\int _0^1 F((1-\rho )\beta ^*+\rho \hat{\beta }_w) d\rho \cdot (\hat{\beta }_w - \beta ^*)-\sqrt{n}s(\beta ^*) \\&\quad = \Big [F(\hat{\beta }_w)-\int _0^1 F((1-\rho )\beta ^*+\rho \hat{\beta }_w) d\rho \Big ]\cdot \sqrt{n}(\hat{\beta }_w-\beta ^*)-\sqrt{n}s(\beta ^*). \end{aligned}$$

For $G_n=O(p_n)$, by applying Theorem 3, we obtain

$$\begin{aligned} \big \Vert (1-\rho )\beta ^*+\rho \hat{\beta }_w-\beta ^*\big \Vert \le \rho \Vert \hat{\beta }_w-\beta ^*\Vert {\mathop {\longrightarrow }\limits ^{P}} 0. \end{aligned}$$

Since $F(\cdot )$ is a continuous function,

$$\begin{aligned} \Big \Vert \Big |F(\hat{\beta }_w)-\int _0^1 F((1-\rho )\beta ^*+\rho \hat{\beta }_w) d\rho \Big \Vert \Big |{\mathop {\longrightarrow }\limits ^{P}} 0. \end{aligned}$$

Thus

$$\begin{aligned} \frac{\sqrt{n}}{a}\cdot F(\hat{\beta }_w)(\tilde{\beta }_w-\beta ^*)=-\sqrt{n}s(\beta ^*)+o_P(1). \end{aligned}$$

We have $F(\hat{\beta }_w){\mathop {\longrightarrow }\limits ^{P}}F(\beta ^*)$ due to $\hat{\beta }_w{\mathop {\longrightarrow }\limits ^{P}}\beta ^*$. By Slutsky’s lemma, we thus have

$$\begin{aligned} \sqrt{n}(\tilde{\beta }_w-\beta ^*){\mathop {\longrightarrow }\limits ^{d}} N(0,\Sigma ) \ \text {as}\ n\rightarrow \infty . \end{aligned}$$

$\Box$

Proof of Theorem 5:

Note that

$$\begin{aligned} \frac{1}{a}F(\hat{\beta }_w)(\tilde{\beta }_w-\beta ^*)=\Big [F(\hat{\beta }_w)-\int _0^1 F((1-\rho )\beta ^*+\rho \hat{\beta }_w) d\rho \Big ](\hat{\beta }_w-\beta ^*)-s(\beta ^*),\ \rho \in (0,1), \end{aligned}$$

we then obtain

$$\begin{aligned} \frac{1}{a}(\tilde{\beta }_w-\beta ^*)= & {} F(\hat{\beta }_w)^{-1} \Big [F(\hat{\beta }_w)-\int _0^1 F((1-\rho )\beta ^*+\rho \hat{\beta }_w) d\rho \Big ]\cdot ( \hat{\beta }_w -\beta ^*) \\&-(F(\hat{\beta }_w)^{-1}F(\beta ^*))\cdot F(\beta ^*)^{-1} s(\beta ^*),\ \beta _w\in B_\delta . \end{aligned}$$

It is observed that

Then

$$\begin{aligned} E\Vert \hat{\beta }_A-\beta ^*\Vert ^2= & {} \text {tr}(\text {cov}(\hat{\beta }_A))+\Vert E(\hat{\beta }_A)-\beta ^*\Vert ^2=\frac{1}{G_n}\text {tr}(\text {cov}(\hat{\beta }_{n,1}))+\Vert E(\hat{\beta }_{n,1})-\beta ^*\Vert ^2 \\= & {} \frac{1}{G_n} E\Vert \hat{\beta }_{n,1}-\beta ^*\Vert ^2+\Vert E(\hat{\beta }_{n,1}-\beta ^*)\Vert ^2 \\\le & {} \frac{1}{G_n}\bigg [\frac{2\text {tr}(\Sigma )G_n}{n}+O(G_n^2n^{-2})\bigg ]+\bigg [\frac{C_GG_n}{n}+O(G_n^2n^{-2})\bigg ]^2\\= & {} \frac{2\text {tr}(\Sigma )}{n}+O(G_nn^{-2})+O(G_n^2n^{-2}). \end{aligned}$$

By Hölder’s inequality, we have

$$\begin{aligned} \frac{1}{a^2}\cdot E\Big [ \big \Vert F(\hat{\beta }_w)^{-1} \Big (F(\hat{\beta }_w)- & {} \int _0^1 F((1-\rho )\beta ^*+\rho \hat{\beta }_w) d\rho \Big )\cdot ( \hat{\beta }_w -\beta ^*)\big \Vert ^2 \Big ] \\\le & {} \lambda _F^{-2} \sqrt{E\Big [\big \Vert \big |F(\hat{\beta }_w) - \int _0^1 F((1-\rho )\beta ^*+\rho \hat{\beta }_w) d\rho \big \Vert \big |^4\Big ]}\\&\cdot \sqrt{E[\Vert \hat{\beta }_w - \beta ^*\Vert ^4]}\\= & {} O(n^{-2})+O(G_n^4n^{-4}),\lambda _F^{-1}=\Vert |F(\beta ^*)^{-1})\Vert |. \end{aligned}$$

Applying $(b+c)^2\le 2(b^2+c^2)$, we obtain

$$\begin{aligned} E[\Vert \tilde{\beta }_w-\beta ^*\Vert ^2]\le & {} 2E\bigg \{\big \Vert F(\beta ^*)^{-1} \Big [F(\hat{\beta }_w) - \int _0^1 F((1-\rho )\beta ^*+\rho \hat{\beta }_w) d\rho \Big ]\cdot ( \hat{\beta }_w -\beta ^*)\big \Vert ^2 \bigg \} \\&+2E[\Vert |(F(\hat{\beta }_w)^{-1}F(\tilde{\beta }_w))\Vert |^2]\cdot E[\Vert F(\tilde{\beta }_w)^{-1}s(\beta ^*)\Vert ^2] \\\le & {} O(n^{-2})+O(G_n^4n^{-4}) +2E[\Vert |(F(\tilde{\beta })^{-1}F(\beta ^*))\Vert |^2]\\\le & {} 2 E[\Vert F(\beta ^*)^{-1}s(\beta ^*)\Vert ^2] +O(n^{-2})+O(G_n^4n^{-4}).\ (\text {through Theorem 4}) \end{aligned}$$

$\Box$

Proof of Theorem 6:

Noting that

$$\begin{aligned} P(e_{g,k}=1)=\frac{r_g}{n} \ (g=1,2,\ldots ,G_n), \end{aligned}$$

we have $Ee_{g,k}=r_g/n$ in (2.2). By Hoeffding’s inequality, we have, for $t>0$,

$$\begin{aligned} P\Big (\frac{1}{n}\big |\sum _{k=1}^n e_{g,k}-r_g \big |>t \Big ) \le 2 e^{-2n^2 t^2}. \end{aligned}$$

Let $t=\varepsilon$, we obtain

$$\begin{aligned} P\Big (\frac{1}{n}\big |\sum _{k=1}^n e_{g,k}-r_g \big |>\varepsilon \Big ) \le 2 e^{-2n^2 \varepsilon ^2}\rightarrow 0\quad \text {as}\ n\rightarrow \infty . \end{aligned}$$