Summary
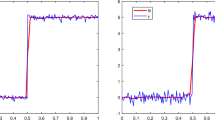
This paper introduces a new nonparametric estimator of the regression based on penalized regression splines. Local roughness penalties that rely on local support properties of B-splines are introduced in order to deal with the spatial heterogeneity of the function to be estimated. This estimator is shown to attain optimal rates of convergence. Then its good performances are confirmed on a simulation study.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
Notes
1 Their Matlab programs are available at the address: http://www.orie.cornell.edu/~davidr/matlab/. The function srslocal was used to perform the estimation.
References
Agarwal, G. and Studden, W. (1980). Asymptotic integrated mean square error using least squares and bias minimizing splines. Ann. Statist., 8, 1307–1325.
Besse, P., Cardot, H., and Ferraty, F. (1997). Simultaneous nonparametric regressions of unbalanced longitudinal data. Computational Statistics and Data Analysis, 24, 255–270.
Burman, P. and Chen, K.W. (1989). Nonparametric estimation of a regression function. Ann. Statist., 17, 1567–1596.
Cardot, H. (2000). Nonparametric estimation of smoothed principal components analysis of sampled noisy functions. Nonparametric Statistics, 12, 503–538.
de Boor, C. (1978). A Practical Guide to Splines. Springer, New-York.
Dierckx, P. (1993). Curve and Surface Fitting with Splines. Clarendon Press, Oxford.
Denison, D.G.T., Mallick, B.K. and Smith, A.F.M. (1998). Automatic Bayesian curve fitting. J. R. Statist. Soc. B, 60, 333–350.
Diack, C.A.T. and Thomas, C. (1998). A nonparametric test of the non convexity of the regression. Nonparametric Statistics, 9, 335–362.
Eilers, P.H.C and Marx, B.D. (1996). Flexible Smoothing with B-splines and Penalties (with discussion). Statistical Science, 11, 89–121.
Friedman, J.H. (1991). Multivariate adaptive regression splines (with discussion). Annals of Stat., 19, 1–141.
Green, P.J. and Silverman, B.W. (1994). Nonparametric Regression and Generalized Linear Models. Chapman and Hall.
Kelly, C. and Rice, J. (1990). Monotone smoothing with application to dose-response curves and the assessment of synergism. Biometrics, 46, 1071–1085.
O’Sullivan, F. (1986). A Statistical Perspective on Ill-Posed Inverse Problems. Statistical Science, 4, 502–527.
Ruppert, D. and Carrol, R.J. (2000). Spalially-adaptive penalties for spline smoothing. Australian and New Zealand Journal of Statistics, 42, 205–223.
Vieu, P. (1991). Nonparametric Regression: Optimal Local Bandwith Choice J. R. Statist. Soc. B, 53, 453–464.
Wand, M. P. (2000). A comparison of regression spline smoothing procedures. Comput. Statist., 15, 443–462.
Zhou, S., Shen, X. and Wolfe, D.A. (1998). Local Asymptotics for Regression Splines and Confidence Regions. Annals of Stat., 26, 1760–1782.
Acknowledgements
I’m indebted to M. Goulard, P. Sarda and A. Trubuil for helpful discussions which improved this manuscript in various ways.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Cardot, H. Local roughness penalties for regression splines. Computational Statistics 17, 89–102 (2002). https://doi.org/10.1007/s001800200092
Published:
Issue Date:
DOI: https://doi.org/10.1007/s001800200092