Abstract
We introduce a measure for the riskiness of cooperation in the infinitely repeated discounted Prisoner’s Dilemma and use it to explore how players cooperate once cooperation is an equilibrium. Riskiness of a cooperative equilibrium is based on a pairwise comparison between this equilibrium and the uniquely safe all defect equilibrium. It is a strategic concept heuristically related to Harsanyi and Selten’s risk dominance. Riskiness 0 defines the same critical discount factor \(\delta ^{*}\) that was derived with an axiomatic approach for equilibrium selection in Blonski et al. (Am Econ J 3:164–192, 2011). Our theory predicts that the less risky cooperation is the more forgiving can parties afford to be if a deviator needs to be punished. Further, we provide sufficient conditions for cooperation equilibria to be risk perfect, i.e. not to be risky in any subgame, and we extend the theory to asymmetric settings.

Similar content being viewed by others
Notes
In this context it is noteworthy, that even Harsanyi and Selten did not agree on this point and Harsanyi (1995) later came up with an alternative selection theory where he decided to reverse priority and favour risk dominance over payoff dominance.
Then discounted payoffs from playing cooperation indefinitely, \(\frac{3}{ 1-\delta }\), offset those from defecting unilaterally and being kept at the minimax thereafter, \(\frac{10}{3}+\frac{7}{3}\frac{\delta }{1-\delta }\).
Note that picking a different equilibrium corresponds to a different game \( \Gamma ^{*}\).
There is another (weak) mixed equilibrium which is not of interest here.
This point was raised by Aumann (1990) who used this same example to motivate his objection against the self enforcing nature of Nash equilibria. Ellingson and Ostling (2010) recently proposed a new perspective on how communication could affect strategic risk in static games that could in principle be extended to our environment.
Payoff differences (incentives to switch to another strategy) for any given opponent’s behavior remain unchanged.
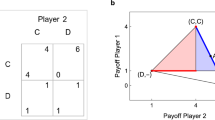
The Nash product is the product of both players’ disincentives not to behave according to the equilibrium under consideration. In our example \( D^{*}\) risk dominates \(C^{*}\) because \((7-0)(7-0)=49>1=(9-8)(9-8)\). We picked these numbers because \(\Gamma ^{*}\) has made a career into game theory textbooks (see for example Fudenberg and Tirole 1991, p. 21) as an example for a game where the selection criteria payoff dominance and risk dominance conflict with each other.
Note that Blonski et al. (2011), though already published, was written after the first version of this article.
Recent experimental evidence by Fudenberg et al. (2012) is consistent with this theoretical observation, though their experiments are not specifically tailored to it.
In Sect. 6 we allow for parameter asymmetries and find that definitions and results are qualitatively unchanged. In order to economize on notation we use \(c,d\) as lables for the stage game strategies as well as for payoff parameters as long as there is no confusion.
The first parameter restriction implies the PD while the second restriction excludes cases where indefinite cooperation is not efficient since patient players can improve by defecting alternately.
In the defect equilibrium both players use the same strategy. As long as this does not cause confusion we identify the strategy and the corresponding equilibrium profile with the same symbol \(\omega \).
Since continuation payoffs are always \(\frac{c}{1-\delta }\) or \(\frac{d}{ 1-\delta }\) if both players pick \(\varphi \) or \(\omega \) we simplify the notation. For example \(V_{1\omega }\) is the continuation payoff of player 1 playing strategy \(\omega \) if player 2 plays \(\varphi _{2}\)
Although our main interest is to explore favorable conditions for cooperation obviously the same question can be asked for every other equilibrium of the repeated PD game, also for inefficient equilibria.
To avoid introducing further notation we do not provide a formal definition of simple strategies and optimal penal codes. The details are well known, and we do not need them here; see Abreu (1988).
We do not study here the consequences of trading effects among players with different discount factors. It is well known (see for example Lehrer and Pauzner 1999) that there are positive gains from trade between an impatient and a patient player that enhance the set of equilibrium payoffs. In this setting the cooperation equilibrium is not necessarily efficient and thereby may not the “natural candidate” to compare with all-defect for assessing risk. However, to keep things simple in this section we restrict attention to cooperation equilibria.
A relevant difference is the possibility to punish more severely in the continuous strategy repeated game. This enlarges the feasable range of differentiating continuation payoffs which—as we pointed out in the previous section—can mitigate the problem to some extent.
In a cooperation equilibrium by definition no player can gain by deviating from indefinite cooperation.
References
Abreu D (1988) On the theory of infinitely repeated games with discounting. Econometrica 56:383–396
Aumann R (1990) Nash equilibria are not enforceable. In: Gabszewitz JJ et al. (eds) Economic decision making. Elsevier Science Publishers, Amsterdam, pp 201–206
Blonski M, Ockenfels P, Spagnolo G (2011) Equilibrium selection in the repeated Prisoner’s dilemma: axiomatic approach and experimental evidence. Am Econ J 3:164–192
Carlsson H, van Damme E (1993) Global games and equilibrium selection. Econometrica 61:989–1018
Carlsson H, van Damme E (1993) Equilibrium selection in stag hunt games. In: Binmore K and Kirman A (eds) Frontiers in game theory. MIT Press, Cambridge, pp 237–254
Ellingson T, Ostling R (2010) When does communication improve coordination? Am Econ Rev 100:1695–1724
Farrell J, Maskin E (1989) Renegotiation in repeated games. Games Econ Behav 1:327–360
Friedman JW (1971) A non-co-operative equilibrium for supergames. Rev Econ Stud 38:1–12
Fudenberg D, Maskin E (1986) The Folk theorem in repeated games with discounting or with incomplete information. Econometrica 54:533–556
Fudenberg D, Tirole J (1991) Game Theory. MIT Press, Cambridge
Fudenberg D, Rand DG, Dreber A (2012) Slow to anger and fast to forgive: cooperation in an uncertain world. Am Econ Rev 100 (forthcoming)
Harsanyi JC, Selten R (1988) A general theory of equilibrium selection in games. MIT Press, Boston
Harsanyi JC (1995) A new theory of equilibrium selection for games with complete information. Games Econ Behav 8:91–122
Kandori M, Mailath G, Rob R (1993) Learning, mutation, and long run equilibria in games. Econometrica 61:29–56
Lehrer E, Pauzner A (1999) Repeated games with differential time preferences. Econometrica 67:393–412
Schmidt D, Shupp R, Walker JM, Ostrom E (2003) Playing safe in coordination games: the roles of risk dominance, payoff dominance, and history of play. Games Econ Behav 42:281–299
van Damme E (1989) Renegotiation-proof equilibria in repeated Prisoner’s dilemma. J Econ Theory 47:206–217
van Damme E, Hurkens S (1998) Endogenous price leadership. MIMEO
van Damme E, Hurkens S (1999) Endogenous stackelberg leadership. Games Econ Behav 28:105–129
van Huyck JB, Battalio RC, Beil RO (1990) Tacit coordination games, strategic uncertainty, and coordination failure. Am Econ Rev 80:234–248
Young P (1993) The evolution of conventions. Econometrica 61:57–84
Acknowledgments
We appreciate suggestions and remarks by an anonymous referee, Geir Asheim, Eric van Damme, Christian Ewerhart, David Levine, Klaus Ritzberger, Reinhard Selten and various seminar participants in Berkeley, Bonn, Frankfurt, Mannheim, Stanford, Stockholm, Tilburg, and Zürich. This Project has been supported by Grants from the DFG (BL418/4-1) for Blonski, and from the European Commission (EGEMTPS/RTN) for Spagnolo.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
1.1 The bicentric prior and the tracing procedure in the infinitely repeated Prisoner’s Dilemma
Harsanyi and Selten’s more general definition of risk dominance is based on the so called bicentric prior and the tracing procedure and is difficult to check for games with many strategies. This might explain why it rarely found its way into the applied literature with the exception of \( 2\times 2\)-games with two strict equilibrium points (see Harsanyi and Selten (1988), Chap. 3). While the bicentric prior and the tracing procedure have ever been controversial among game theorists they offer no clue in our context since HS defined them only for finite games. The game theoretic literature has not yet offered a generalization of risk dominance to infinite games. We learned from Klaus Ritzberger that a fundamental mathematical difficulty does not allow a direct generalization of the tracing procedure to infinite games. The idea of the tracing procedure relies on connecting strategy profiles by a generically unique continuous path representing continuous adjustment of beliefs. The problem is that this continuous path is neither unique nor even defined if equilibria are not topologically isolated which happens to be the case in infinite games. In finite games, in contrast, equilibria can shown to be generically isolated.
The bicentric prior—loosely speaking—is a mixed strategy profile reflecting players’ initial beliefs on which of two equilibria under comparison should be played. More precisely, say, player \(-i\) attaches subjective probability \(\left( z,1-z\right) \) to strategies \(\varphi _{-i},\omega _{-i}\). Since player \(i\) has no idea of player \(-i\)’s subjective probability HS invoke the principle of insufficient reason and let player \(i\)’s bicentric prior \(p_{i},1-p_{i}\) be defined as a best response on the mixture \(\left( Z,1-Z\right) \) where \(Z\) is a random variable uniformly distributed over \(\left[ 0,1\right] \). Since generally the bicentric prior is not an equilibrium in itself HS define the tracing procedure such as to readjust beliefs to obtain the risk-dominant equilibrium. To do this precisely, define the payoffs of a parametrized family of auxiliary games denoted by \(\Gamma ^{t}\left( \delta ,p\right) \) as follows. Consider strategy profile \(\xi =\left( \xi _{1},\xi _{2}\right) \) of \(\Gamma \left( \delta \right) \). Let player \(i\) assume that player \(-i\) plays his bicentric prior abbreviated by \(p_{-i}\) with probability \(\left( 1-t\right) \) and \(\xi _{-i}\) with probability \(t\) such that player \(i\) obtains
The so defined game \(\Gamma ^{t}\left( \delta ,p\right) \) can be interpreted as a convex combination of the original game \(\Gamma \left( \delta \right) \) and the trivial game where each player plays against his bicentric prior. Denote by \(G=\left\{ \left( t,\xi \right) \left| \xi \text { is an equilibrium for }\Gamma ^{t}\left( \delta ,p\right) \right. \right\} \) the graph of the equilibrium correspondence for the \(t\)-parametrized family of games \(\Gamma ^{t}\left( \delta ,p\right) \).
For generic finite games it can be shown that \(G\) contains a unique distinguished curve connecting the best reply (which is the equilibrium) of \( \Gamma ^{0}\left( \delta ,p\right) \) equilibrium with one of the two given equilibria (either \(\varphi \) or \(\omega \)) in \(\Gamma ^{1}\left( \delta ,p\right) \) for almost any prior \(p\). Unfortunately, this is not anymore the case for infinite games. Therefore, for the purpose of the present paper we cannot follow the tracing procedure in order to define risk dominance.
Our criteria for an appropriate model of strategic risk in our context are (i) it must be defined for the discounted infinitely repeated Prisoner’s Dilemma, (ii) it should capture the intuitive observation that payoff \(a\) enters the propensity to cooperate, (iii) be as simple as possible (Ockham’s razor). HS’s theory at least fails on criteria (i) and (iii) and clearly any extension of it would fail to a larger extent on (iii). It also fails on criterion (ii) since at least in their famous book HS impose priority for payoff-dominance over risk-dominance whenever the two concepts contradict. The cooperative equilibrium payoff-dominates the all-defect equilibrium whenever it exists. Hence, parameter \(a\) does not infuence equilibrium selection with respect to the HS theory.
As already mentioned, it is known that for finite games with more than two strategies risk dominance within \(\Gamma _{\varphi }\) and risk dominance based on the bicentric prior and the tracing procedure can differ (see van Damme and Hurkens 1998, 1999; and Carlsson and van Damme 1993b). For example, it may be the case that the best reply against the bicentric prior puts some positive weight on a third strategy which is not among the two equilibria under comparison and thereby tilts the bicentric prior tracing procedure comparison to another direction than the direct comparison does. As we have seen this concern is not well defined within the repeated PD. To the contrary, we note that here we do not compare two arbitrary equilibria of the repeated PD game. Rather, we compare a cooperation equilibrium \( \varphi \) with the uniquely “safe” all-defection equilibrium \(\omega \). For this comparison there is a best reply to the bicentric prior that is independent of the auxiliary game parameter \(t\). One such best reply against different mixtures parametrized by \(t\) is always either all defect \(\omega \) or grim trigger denoted by \(\psi \). There is no potential gain in playing any other cooperation strategy since grim trigger is payoff-equivalent with all other cooperation strategies against another cooperation strategy Footnote 19 but is better than any other cooperation strategy against all defect while all defect is a best response against all defect.
To see that the direct risk comparison in this paper is in line with the belief adjustment according to this constant best response to the bicentric prior (instead of the tracing procedure which is not well defined) we compute player \(i\)’s bicentric prior by defining expected payoffs of responding to the joint mixture \(z\varphi _{-i}+\left( 1-z\right) \omega _{-i}\) by either of the pure strategies \(\psi _{i}\) or \(\omega _{i}\):
Now compare these expected payoffs making use of \(u_{i}\left( \varphi \right) =\frac{c}{1-\delta }-b-\delta V_{i\omega }\) and \(v_{i}\left( \psi \right) =\frac{d}{1-\delta }-a-\delta \frac{d}{1-\delta }=d-a:\)
Player \(i\)’s bicentric prior probabilities are given by the lengths of the subintervals \(\left[ z,1\right] \) and \(\left[ 0,z\right] \):
Since the tracing procedure is not well defined we now turn to a constant (in \(t\)) best response to the bicentric prior. At the starting point \(t=0\) player \(i\) picks a best response to his bicentric prior \(p_{-i}:=p_{-i}\psi _{-i}+\left( 1-p_{-i}\right) \omega _{-i}\). For any \(t\in \left( 0,1\right) \) responding to \(p_{-i}\) by playing \(\varphi _{i}\) or \(\omega _{i}\) yields the payoff comparison
This shows in the language of HS that \(U_{i}\left( \omega _{i},p_{-i}\right) >U_{i}\left( \varphi _{i},p_{-i}\right) \) for \(i=1,2\) iff \(\omega \)’s Nash product \(v_{i}\left( \varphi \right) v_{-i}\left( \varphi \right) \) is strictly larger than \(\varphi \)’s Nash product \(u_{i}\left( \varphi \right) u_{-i}\left( \varphi \right) \). In this case an equilibrium in \(\Gamma ^{t}\left( s,p\right) \) contains no positive weight on \(\varphi \) for any \( t\in \left( 0,1\right) \) since \(\omega \) outperforms \(\varphi \) against the bicentric prior \(p\) and the constant best response \(p_{-i}\). The converse holds for \(U_{i}\left( \varphi _{i},p_{-i}\right) >U_{i}\left( \omega _{i},p_{-i}\right) \). This shows that this form of belief adjustment corresponds exactly to our definition of risk dominance within the \(2\times 2\)-game\(\ \Gamma _{\varphi }\).
Rights and permissions
About this article
Cite this article
Blonski, M., Spagnolo, G. Prisoners’ other Dilemma. Int J Game Theory 44, 61–81 (2015). https://doi.org/10.1007/s00182-014-0419-9
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00182-014-0419-9
Keywords
- Cooperation
- Repeated Prisoner’s Dilemma
- Equilibrium selection
- Forgiveness
- Perfection
- Strategic risk
- Strategic uncertainty
- Sucker’s payoff
- Collusion
- Coordination