Abstract
Predicate encryption (PE), a generalization of attribute-based encryption (ABE), is a versatile tool for providing access control over data. The underlying predicate for a PE is parametrized by an index, called system parameter or simply system-index. A system-index, in general, consists of component(s) from \(\mathbb {N}\). Yamada et al. in PKC 2011 proposed a verifiability-based conversion from CPA to CCA-secure ABE. This conversion was generalized by Yamada et al. in PKC 2012 from ABE to PE. In the later conversion, the authors considered the system-index to be a single component. In practice, there are many schemes, e.g., functional encryption for general relations and hierarchical-inner product (HIP) encryption schemes of Okamoto-Takashima in CRYPTO 2010, CANS 2011 and EUROCRYPT 2012, where system-indices consist of more than a single component. Therefore, for these schemes, the conversion of Yamada et al. (in PKC, 2012) is out of scope. In this paper, we revisit the CPA to CCA conversion for PE and propose a new conversion based on verifiability. The proposed conversion works irrespective of the number of components in the system-indices. It generalizes the existing conversion of Yamada et al. (in PKC, 2011) from ABE to PE. The PE schemes which are realized by the conversion of Yamada et al. (2011) are also realized by our conversion. Therefore, the conversion of ours has more scope than the conversion proposed in 2012. We show that all the aforementioned CPA-secure schemes for general relations and HIP relation are easily converted to the corresponding CCA-secure schemes by our conversion. Further, we show a generic conversion from CPA to CCA-secure functional encryption for regular languages which captures the existing PE schemes for regular languages.


Similar content being viewed by others
Notes
A PE with public index hides only the message, whereas a PE with hidden index conceals both the message and the data-index.
These are 2-threshold gates, one may consider general threshold gates, e.g., t-threshold gates.
\(\mathcal {T}_0\) maps the system-index \(\varvec{j}\) of \(\mathsf{PE}\) to the system-index \(\varvec{j}'\) of \(\mathsf{PE}'\). However, we omit the technical details of \(\mathcal {T}_0\) throughout this chapter as it does not harm in understanding the actual conversion.
The ABE schemes [17] for circuits are not known to have either public verifiability or verifiability-1. So, the CCA-secure realization of the schemes is still unknown. We remark that if there is an efficient algorithm for testing the group membership of the underlying multilinear maps [16], then one can have the public verifiability using the property of the multilinear maps.
If \(0,1\in \varSigma \), then consider two special symbols say \(\tilde{\sigma }_0, \tilde{\sigma }_1\) such that \(\tilde{\sigma }_0, \tilde{\sigma }_1 \not \in \varSigma \) and set \(\varSigma ' := \varSigma \cup \{\tilde{\sigma }_0, \tilde{\sigma }_1\}\) and \(\mathsf{Tr}'\) is replaced by \(\mathsf{Tr}' := \mathsf{Tr}\cup \{(q'_{i-1}, q'_i, \tilde{\sigma }_{\mathsf{vk}[i]})\ :\ i\in [n]\}\)
A decrypt query on \((\mathsf{CT}, x)\) is called valid if its returned value is not \(\perp \). We note that for a decrypt query \((\mathsf{CT}, x)\) of the form \((\mathsf{CT}= \mathsf{CT}^*\wedge x\thicksim y)\) or
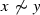 , the simulator always returns \(\perp \).
, the simulator always returns \(\perp \).
References
Attrapadung, N.: Dual system encryption via doubly selective security: framework, fully secure functional encryption for regular languages, and more. In: EUROCRYPT, volume 8441 of LNCS, pp. 557–577. Springer (2014)
Attrapadung, N.: Fully secure and succinct attribute based encryption for circuits from multi-linear maps. Cryptology ePrint Archive, Report 2014/772 (2014). http://eprint.iacr.org/
Attrapadung, N., Libert, B.: Functional encryption for inner product: achieving constant-size ciphertexts with adaptive security or support for negation. In: PKC, volume 6056 of LNCS, pp. 384–402. Springer (2010)
Attrapadung, N., Libert, B., de Panafieu E.: Expressive key-policy attribute-based encryption with constant-size ciphertexts. In: Public Key Cryptography, volume 6571 of LNCS, pp. 90–108. Springer (2011)
Beimel, A.: Secure schemes for secret sharing and key distribution (1996). http://www.shoup.net/papers/
Bethencourt, J., Sahai, A., Waters, B.: Ciphertext-policy attribute-based encryption. In: IEEE Symposium on Security and Privacy, pp. 321–334. IEEE Press (2007)
Blömer, J., Liske, G.: Construction of fully cca-secure predicate encryptions from pair encoding schemes. In: CT-RSA, volume 9610 of LNCS, pp. 431–447. Springer (2016)
Boneh, D., Franklin, M.: Identity-based encryption from the weil pairing. In: CRYPTO, volume 2139 of LNCS, pp. 213–229. Springer (2001)
Boneh, D., Hamburg, M.: Generalized identity-based and broadcast encryption schemes. In: ASIACRYPT, volume 5350 of LNCS, pp. 455–470. Springer (2008)
Boneh, D., Katz, J.: Improved efficiency for CCA-secure cryptosystems built using identity-based encryption. In: CT-RSA, volume 3376 of LNCS, pp. 87–103. Springer (2005)
Boneh, D., Sahai, A., Waters, B.: Functional encryption: definitions and challenges. In: TCC, volume 6597 of LNCS, pp. 253–273. Springer (2011)
Canetti, R., Halevi, S., Katz, J.: Chosen-ciphertext security from identity-based encryption. In: EUROCRYPT, volume 3027 of LNCS. Springer (2004)
Cocks, C.: An identity based encryption scheme based on quadratic residues. In: Cryptography and Coding, volume 2260 of LNCS, pp. 360–363. Springer (2001)
Diffie, W., Hellman, M.: New directions in cryptography. IEEE Trans. Inf. Theory 22(6), 644–654 (1976)
Fujisaki, E., Okamoto, T.: Secure integration of asymmetric and symmetric encryption schemes. In: CRYPTO, volume 1666 of LNCS, pp. 537–554. Springer (1999)
Garg, S., Gentry, C., Halevi, S.: Fcandidate multilinear maps from ideal lattices. In: EUROCRYPT, volume 7881 of LNCS, pp. 1–17. Springer (2013)
Garg, S., Gentry, C., Halevi, S., Sahai, A., Waters, B.: Attribute-based encryption for circuits from multilinear maps. In: CRYPTO, volume 8043 of LNCS, pp. 479–499. Springer (2013)
Gorbunov, S., Vaikuntanathan, V., Wee, H.: Attribute-based encryption for circuits. In: Proceedings of the Forty-Fifth Annual ACM Symposium on Theory of computing, pp. 545–554. ACM (2013)
Goyal, V., Jain, A., Pandey, O., Sahai, A.: Bounded ciphertext policy attribute based encryption. In: Automata, Languages and Programming, volume 5126 of LNCS, pp. 579–591. Springer (2008)
Goyal, V., Pandey, O., Amit, S., Waters, B.: Attribute-based encryption for fine-grained access control of encrypted data. In: ACM Conference on Computer and Communications Security, pp. 89–98. ACM (2006)
Halevi, S., Micali, S.: Practical and provably-secure commitment schemes from collision-free hashing. In: CRYPTO, volume 1109 of LNCS, pp. 201–215. Springer (1996)
Hamburg, M.: Spatial encryption. Cryptology ePrint Archive, Report 2011/389 (2011). http://eprint.iacr.org/
Katz, J., Sahai, A., Waters, B.: Predicate encryption supporting disjunctions, polynomial equations, and inner products. In: EUROCRYPT, volume 4965 of LNCS, pp. 146–162. Springer (2008)
Lewko, A.B., Okamoto, T., Sahai, A., Takashima, K., Waters, B.: Fully secure functional encryption: attribute-based encryption and (hierarchical) inner product encryption. In: EUROCRYPT, volume 6110 of LNCS, pp. 62–91. Springer (2010)
Nandi, M., Pandit, T.: On the power of pair encodings: frameworks for predicate cryptographic primitives. Cryptology ePrint Archive, Report 2015/955 (2015). http://eprint.iacr.org/
Okamoto, T., Takashima, K.: Hierarchical predicate encryption for inner-products. In: ASIACRYPT, volume 5912 of LNCS, pp. 214–231. Springer (2009)
Okamoto, T., Takashima, K.: Fully secure functional encryption with general relations from the decisional linear assumption. In: CRYPTO, volume 6223 of LNCS, pp. 191–208. Springer (2010)
Okamoto, T., Takashima, K.: Achieving short ciphertexts or short secret-keys for adaptively secure general inner-product encryption. In: Cryptology and Network Security, volume 7092 of LNCS, pp. 138–159. Springer (2011)
Okamoto, T., Takashima, K.: Adaptively attribute-hiding (hierarchical) inner product encryption. In: EUROCRYPT, volume 7237 of LNCS, pp. 591–608. Springer (2012)
Okamoto, T., Takashima, K.: Fully secure unbounded inner-product and attribute-based encryption. In: ASIACRYPT, volume 7658 of LNCS, pp. 349–366. Springer (2012)
Ostrovsky, R., Sahai, A., Waters, B.: Attribute-based encryption with non-monotonic access structures. In: ACM Conference on Computer and Communications Security, pp. 195–203 (2007)
Sahai, A., Waters, B.: Fuzzy identity-based encryption. In: EUROCRYPT, volume 3494 of LNCS, pp. 457–473. Springer (2005)
Shamir, A.: Identity-based cryptosystems and signature schemes. In: CRYPTO, LNCS, pp. 47–53. Springer (1984)
Waters, B.: Ciphertext-policy attribute-based encryption: an expressive, efficient, and provably secure realization. In: Public Key Cryptography, volume 6571 of LNCS, pp. 53–70. Springer (2011)
Waters, B.: Functional encryption for regular languages. In: CRYPTO, volume 7417 of LNCS, pp. 218–235. Springer (2012)
Yamada, S., Attrapadung, N., Hanaoka, G., Kunihiro, N.: Generic constructions for chosen-ciphertext secure attribute based encryption. In: Public Key Cryptography, volume 6571 of LNCS, pp. 71–89. Springer (2011)
Yamada, S., Attrapadung, N., Santoso, B., Schuldt, J.C.N., Hanaoka, G., Kunihiro, N.: Verifiable predicate encryption and applications to cca security and anonymous predicate authentication. In: Public Key Cryptography, volume 7293 of LNCS, pp. 243–261. Springer (2012)
Author information
Authors and Affiliations
Corresponding author
Appendices
A Security of predicate encryption
Definition 8
(Adaptive-predicate IND-CCA security) A PE scheme is said to be IND-CCA secure in adaptive-predicate model (or AP-IND-CCA secure) if for all PPT algorithms \(\mathscr {A}:= (\mathscr {A}_1, \mathscr {A}_2)\), the advantage
in \(\mathsf{Exp}_{\mathscr {A}, \mathsf{PE}}^\mathrm{AP-IND-CCA} (\kappa )\) defined in Fig. 3 is negligible function in security parameter \(\kappa \), where \(\mathscr {A}\) is provided access to key-gen oracle \(\mathcal {O}_{K}\) and decrypt oracle \(\mathcal {O}_{D}\) (described below) with a natural restriction that \((\mathsf{C}^*, x)\) with \(x\thicksim y^*\) was never queried to \(\mathcal {O}_{D}\) and  for each key-index \(x\) queried to \(\mathcal {O}_{K}\).
for each key-index \(x\) queried to \(\mathcal {O}_{K}\).
-
KeyGen oracle (\(\mathcal {O}_{K}\)): Given a key-index \(x\), oracle returns \({\mathcal {SK}}_{x}\longleftarrow \mathsf{KeyGen}({\mathcal {PP}}\), \({\mathcal {MSK}}, x)\).
-
Decrypt oracle (\(\mathcal {O}_{D}\)): Given \((\mathsf{C}, x)\), oracle returns \(\mathsf{Decrypt}({\mathcal {PP}}, \mathsf{C}, {\mathcal {SK}}_{x})\).
We may refer the above security model as AP-IND-CCA security model in this paper.
Definition 9
(Selective-predicate IND-CCA security) Likewise in IND-CCA security in selective-predicate model (or SP-IND-CCA security), the adversary \(\mathscr {A}\) submits the challenge data-index \(y^*\) before receiving \({\mathcal {PP}}\)of PE. In this case, the advantage of \(\mathscr {A}\) is denoted by \(\mathsf{Adv}_{\mathscr {A}, \mathsf{PE}}^\mathrm{SP-IND-CCA} (\kappa )\).
Definition 10
(IND-CPA security) A weaker notion of the above security can be defined similarly as above except, \(\mathscr {A}\) is not given access to \(\mathcal {O}_{D}\) oracle. It is called IND-CPA security in both adaptive-predicate (AP-IND-CPA) and selective predicate (SP-IND-CPA) models. The advantages of \(\mathscr {A}\) in the respective models are denoted by \(\mathsf{Adv}_{\mathscr {A}, \mathsf{PE}}^\mathrm{AP-IND-CPA} (\kappa )\) and \(\mathsf{Adv}_{\mathscr {A}, \mathsf{PE}}^\mathrm{SP-IND-CPA} (\kappa )\).
B One time signature, mac and meak commitment
Definition 11
(Signature scheme) A signature scheme consists of three PPT algorithms - Gen, Sign and Ver.
-
Gen: It takes a security parameter \(\kappa \). It outputs a verification key vk and a signing key signk.
-
Sign: It takes a message \(m\) and a signing key signk as input. It returns a signature \(\delta \).
-
Ver: It receives a message \(m\), a signature \(\delta \) and a verification key vk as input. It returns a boolean value 1 for acceptance or 0 for rejection.
Definition 12
(Strong unforgeability of one-time signature)
Strongly unforgeability one-time signature model is defined as a game, \(\mathrm {Game}_{Real}\) between a challenger \(\mathscr {B}\) and an adversary \(\mathscr {A}\), where the adversary has to forge a signature for a message. The game, \(\mathrm {Game}_{Real}\) consists of the following phases:
Gen: The challenger \(\mathscr {B}\) runs \(\mathsf{Gen}(1^\kappa )\longrightarrow (\mathsf{vk}, \mathsf{signk})\). Then vk is given to the adversary \(\mathscr {A}\).
Query: The adversary \(\mathscr {A}\) is given access to the oracle \(\mathsf{Sign}(.,\mathsf{signk})\) at most once. Let \((m,\delta )\) be the corresponding query message and relied signature.
Forgery: The adversary outputs a signature \((m^*, \delta ^*)\).
We say the adversary succeeds in this game if \(\mathsf{Ver}(m^*, \delta ^*, \mathsf{vk}) = 1\) and \((m,\delta )\ne (m^*, \delta ^*)\).
Let \(\mathsf{Adv}_{\mathscr {A}, \mathrm OTS}^\mathrm{sUF-CMA} (\kappa )\) denote the success probability for any adversary \(\mathscr {A}\) in the above experiment. A signature scheme is said to be strongly unforgeable one-time signature (or simply called strong OTS) if \(\mathsf{Adv}_{\mathscr {A}, \mathrm OTS}^\mathrm{sUF-CMA} (\kappa )\) is at most negligible function in \(\kappa \)
Definition 13
(Message authentication code) A message authentication code (MAC) consists of two algorithms - Mac and MVer.
-
Mac It takes as inputs, a symmetric key \(\mathsf{AK}\in \mathcal {K}\), where \(\mathcal {K}\) is a key space and a message \(m\in \mathcal {M}\) and it outputs tag \(\tau \). In notation, we write \(\tau := \mathsf{Mac}_{\mathsf{AK}}(m).\)
-
MVer It takes the inputs, a symmetric key \(\mathsf{AK}\), a message \(m\) and a tag \(\tau \). It returns 1 for accept and 0 for reject. We use the notation, \(\mathsf{MVer}_{\mathsf{AK}}(m,\tau )\) for \(\mathsf{MVer}(\mathsf{AK},m,\tau )\).
For correctness, it is required that for all \(\mathsf{AK}\in \mathcal {K}\) and all \(m\in \mathcal {M}\) that \(\mathsf{MVer}_{\mathsf{AK}}(m, \mathsf{Mac}_{\mathsf{AK}}(m)) = 1\)
Definition 14
(Message authentication) A message authentication code \((\mathsf{Mac}, \mathsf{MVer})\) is secure against a one-time chosen-message attack if the success probability (denoted by \(\mathsf{Adv}_{\mathscr {A}, \mathrm{MAC}}^\mathrm{sUF-CMA} (\kappa )\))of any PPT adversary \(\mathscr {A}\) in the following game is negligible in the security parameter \(\kappa \):
-
1.
A random key \(\mathsf{AK}\in \mathcal {K}\) is chosen.
-
2.
\(\mathscr {A}\) outputs a message \(m\) and is given in return \(\tau = \mathsf{Mac}_{\mathsf{AK}}(m)\).
-
3.
\(\mathscr {A}\) outputs a pair \((m', \tau ')\).
We say that \(\mathscr {A}\) succeeds in above game if \((m, \tau ) \ne (m', \tau ')\) and \(\mathsf{MVer}_{\mathsf{AK}}(m', \tau ') = 1\).
Definition 15
(Weak commitment) A weak commitment scheme [10] is a triple of PPT algorithms - wCSetup, wCommit and wDecommit.
-
wCSetup: It takes as input a security parameter \(1^\kappa \) and outputs a string pub.
-
wCommit: It takes input pub, and outputs \((\mathsf{AK}, \mathsf{com}, \mathsf{decom})\) with \(\mathsf{AK}\in \{0,1\}^\kappa \). We would say \(\mathsf{com}\) as the public commitment string and \(\mathsf{decom}\) as the de-commitment string.
-
wDecommit: It takes as input pub, \(\mathsf{com}\) and \(\mathsf{decom}\), and outputs a key \(\mathsf{AK}\in \{0,1\}^\kappa \cup {\perp }\).
For correctness, it is required that for all pub generated by \(\mathsf{wCSetup}\) and for all \((\mathsf{AK}, \mathsf{com}, \mathsf{decom})\longleftarrow \mathsf{wCommit}(\mathsf{pub})\), we have \(\mathsf{wDecommit}(\mathsf{pub}, \mathsf{com}, \mathsf{decom}) = \mathsf{AK}\).
Definition 16
(Hiding) A weak commitment scheme is said to have hiding property if for all PPT algorithms \(\mathscr {A}\), the advantage
in \(\mathsf{Exp}_{\mathscr {A}, \mathrm{wCommit}}^\mathrm{Hiding} (\kappa )\) defined in Fig. 4 is negligible function in \(\kappa \).
Definition 17
(Binding) A weak commitment scheme is said to have binding property if for all PPT algorithms \(\mathscr {A}\), the advantage
in \(\mathsf{Exp}_{\mathscr {A}, \mathrm{wCommit}}^\mathrm{Binding} (\kappa )\) defined in Fig. 4 is negligible function in \(\kappa \).
Definition 18
(Security of weak commitment) A weak commitment scheme is said to be secure if it satisfies both hiding property (Definition 16) and binding property (Definition 17).
Practical weak commitment schemes can be constructed (see [10]) using the cryptographic hash function and family of pairwise independent hash.
C The proof of Theorem 1
Here we provide proof of adaptive security. Similarly, one can prove the selective security of the proposed construction. We show that if \(\mathscr {A}\) can break IND-CCA security of the proposed scheme \(\mathsf{PE}\), then we establish an algorithm \(\mathscr {B}\) for breaking IND-CPA security of the primitive predicate scheme \(\mathsf{PE}'\). Let \(\mathcal {CH}\) be a challenger for the CPA-secure primitive scheme \(\mathsf{PE}'\). We describe how \(\mathscr {B}\) interacts with \(\mathcal {CH}\) with the help of \(\mathscr {A}\). Here \(\mathscr {B}\) plays two roles, one as a CCA-challenger of \(\mathscr {A}\) against \(\mathsf{PE}\) and the other as an adversary against the CPA-challenger \(\mathcal {CH}\) for \(\mathsf{PE}'\). We note that \(\mathscr {B}\) cannot make decrypt query in the CPA game with \(\mathcal {CH}\), whereas \(\mathscr {A}\) can make the same in the CCA game with \(\mathscr {B}\). So, the challenging task for \(\mathscr {B}\) is to answer the decrypt queries of \(\mathscr {A}\) with the help of only resource, the key-gen oracle. While responding the queries of \(\mathscr {A}\), \(\mathscr {B}\) does not violate the rule of CPA game with \(\mathcal {CH}\) and it simulates perfectly as a challenger of \(\mathscr {A}\). \(\mathscr {B}\) runs \(\mathsf{OTS.Gen}(1^\kappa )\) to get \((\mathsf{vk}^*, \mathsf{signk}^*)\). The security proof consists of the following phases.
Setup: In the setup phase \(\mathscr {B}\) simply forwards the public parameters \({\mathcal {PP}}\)obtained from \(\mathcal {CH}\) to \(\mathscr {A}\).
Phase 1/2 Query: It consists of the following queries in adaptive manner:
-
KeyGen Query: Let \(x\in \mathcal {X}\) be any queried key-index made by \(\mathscr {A}\). \(\mathscr {B}\) makes a key query for \(x' := \mathcal {T}_1(x)\) to \(\mathcal {CH}\). Then, \(\mathcal {CH}\) replies the key \({\mathcal {SK}}_{x} := {\mathcal {SK}}'_{x'}\) to \(\mathscr {B}\) and the same key is forwarded to \(\mathscr {A}\).
-
Decrypt Query: Let \((\mathsf{CT}, x)\) be a decrypt query by \(\mathscr {A}\), where \(\mathsf{CT}= (\mathsf{C}, \delta , \mathsf{vk})\). Then \(\mathscr {B}\) runs \(\mathsf{OTS.Ver}(\mathsf{C}, \delta , \mathsf{vk})\) and \(\mathsf{Verify}({\mathcal {PP}}, \mathsf{C}, x', \epsilon _{\mathsf{vk}})\), and if both the outputs are 1, it proceeds else returns \(\perp \) to \(\mathscr {A}\). If \(\mathsf{vk}=\mathsf{vk}^*\), \(\mathscr {B}\) aborts the game and \(\textsf {BAD}_{\mathsf{OTS}}\) is set True, else moves to next step. \(\mathscr {B}\) makes a key query for \(\epsilon _{\mathsf{vk}}\) to \(\mathcal {CH}\) and obtains a key K for the index \(\epsilon _{\mathsf{vk}}\). Then, \(\mathscr {B}\) returns \(\mathsf{Decrypt}'_K(\mathsf{C})\) to \(\mathscr {A}\).
Challenge: Suppose \(\mathscr {A}\) submits two equal length messages \(m_0, m_1\in \mathcal {M}\) and a challenge policy \(y^*\) to \(\mathscr {B}\). Then, \(\mathscr {B}\) submits the same messages \(m_0, m_1\in \mathcal {M}\) and a challenge policy \(y^*_{\mathsf{vk}^*} := \mathcal {T}_3(y^*, \mathsf{vk}^*)\) to \(\mathcal {CH}\). Then, \(\mathcal {CH}\) picks \(b\mathop {\longleftarrow }\limits ^{\mathrm {U}}\{0,1\}\) and returns \(\mathsf{C}^*= \mathsf{Encrypt}'({\mathcal {PP}}, m_b, y^*_{\mathsf{vk}^*})\) to \(\mathscr {B}\) as a challenge ciphertext. Now, \(\mathscr {B}\) runs \(\delta ^*\longleftarrow \mathsf{OTS.Sign}(\mathsf{C}^*,\mathsf{signk}^*)\) and returns \(\mathsf{CT}^*:= (\mathsf{C}^*, \delta ^*, \mathsf{vk}^*)\) to \(\mathscr {A}\).
Guess: \(\mathscr {A}\) sends a guess \(b'\) for b to \(\mathscr {B}\) and, then \(\mathscr {B}\) returns the same guess \(b'\) to \(\mathcal {CH}\).
Analysis: As the verification key of OTS has been chosen in the beginning of the game it is easy to define a forging algorithm which forges correctly against the one-time signature whenever \(\textsf {BAD}_{\mathsf{OTS}}\) is True. So, we may assume that \(\textsf {BAD}_{\mathsf{OTS}}\) is not set True throughout. In this case we show the following two claims:
Claim-1 (Correctness). \(\mathscr {B}\) does not violate the rule of CPA game (while interacting with \(\mathcal {CH}\)) as long as \(\mathscr {A}\) does so. In other words, \(\mathscr {B}\) is correct given that \(\mathscr {A}\) is correct.
Claim-2 (Perfectness). Until \(\mathscr {B}\) aborts (i.e., \(\textsf {BAD}_{\mathsf{OTS}}\) occurs), all responses of \(\mathscr {B}\) to \(\mathscr {A}\) are identically distributed with the responses of a CCA-challenger \(\mathcal {CH}_{CCA}\) to \(\mathscr {A}\). In other words, \(\mathscr {B}\) simulates perfectly as a CCA-challenger of \(\mathscr {A}\) in the CCA game.
Assuming the above claims, we have
which concludes the proof.
Proof of Claim-1
By the natural restriction on key queries by \(\mathscr {A}\), we have for each queried key-index \(x\)

For each key query on index \(x'\) by \(\mathscr {B}\), we have

which is required as a natural restriction on key queries by \(\mathscr {B}\).
To answer the decrypt query \((\mathsf{CT}= (\mathsf{C}, \delta , \mathsf{vk}), x)\) of \(\mathscr {A}\), \(\mathscr {B}\) makes a key query to \(\mathcal {CH}\) for the key-index \(\epsilon _{\mathsf{vk}}\) and then, it decrypts the ciphertext using \({\mathcal {SK}}'_{\epsilon _{\mathsf{vk}}}\) instead of \({\mathcal {SK}}'_{x'}\). The condition, \(\mathsf{vk}\ne \mathsf{vk}^*\) implies that

which shows that \(\mathscr {B}\) does not violate the rule of the CPA-game with \(\mathcal {CH}\). \(\square \)
Proof of Claim-2
The key queries are answered according to the original construction. So, we only have to show the perfectness in answering the decrypt queries. Let \(\mathscr {A}\) make a valid decrypt queryFootnote 6 on \((\mathsf{CT}= (\mathsf{C}, \delta , \mathsf{vk}), x)\) with \(x\thicksim y\). By ‘\(\Rightarrow \)’ side of condition (1), we have \(x'\thicksim 'y_{\mathsf{vk}}\). Again, condition (2) gives \(\epsilon _{\mathsf{vk}}\thicksim 'y_{\mathsf{vk}}\). Therefore, we have \(\mathsf{Decrypt}'(\mathsf{C},{\mathcal {SK}}'_{x}) = \mathsf{Decrypt}'(\mathsf{C},{\mathcal {SK}}'_{\epsilon _{\mathsf{vk}}})\) by verifiability-1 of \(\mathsf{PE}'\). \(\square \)
D Construction using MAC, weak commitment and verifiability-1
In this section, we provide a generic construction using MAC, weak commitment scheme and verifiability-1 of the underlying CPA-secure scheme \(\mathsf{PE}'\). This is an analogue of the construction (Sect. 4.2) using OTS scheme. Let \((\mathsf{Mac}, \mathsf{MVer})\) and \((\mathsf{wCSetup}, \mathsf{wCommit}, \mathsf{wDecommit})\) be the MAC and weak commitment scheme respectively. The Setup algorithm of the proposed construction is same as the Setup algorithm described in Sect. 4.2 with the understanding that the public parameters \(\mathsf{pub}\) of the weak commitment scheme and the public parameters (if any) of MAC are included in \({\mathcal {PP}}\). The other three algorithms (with implicit understanding of \({\mathcal {PP}},{\mathcal {MSK}}\)) are described as follows.
-
\(\mathsf{KeyGen}(x):= \mathsf{KeyGen}'(x')\) (in notation: \({\mathcal {SK}}_{x} := {\mathcal {SK}}'_{x'}\)).
-
\(\mathsf{Encrypt}(m, y):\) It runs \((\mathsf{AK}, \mathsf{vk}(=\mathsf{com}), \mathsf{decom}) \longleftarrow \mathsf{wCommit}(\mathsf{pub})\) and returns
$$\begin{aligned} \mathsf{CT}= (\mathsf{C}\longleftarrow \mathsf{Encrypt}'(m||\mathsf{decom}, y_{\mathsf{vk}}), ~\tau \longleftarrow \mathsf{Mac}_{\mathsf{AK}}(\mathsf{C}), \mathsf{vk}). \end{aligned}$$ -
\(\mathsf{Decrypt}_{{\mathcal {SK}}_{x}}(\mathsf{C}, \tau , \mathsf{vk}) = {\left\{ \begin{array}{ll} m&{} \hbox { if } \begin{pmatrix} \mathsf{Verify}({\mathcal {PP}}, \mathsf{C}, x', \epsilon _{\mathsf{vk}}) =1; \\ (m||\mathsf{decom}) \longleftarrow \mathsf{Decrypt}'_{{\mathcal {SK}}'_{x'}}(\mathsf{C});\\ \mathsf{AK}\longleftarrow \mathsf{wDecommit}(\mathsf{pub}, \mathsf{vk}, \mathsf{decom}); \\ \mathsf{MVer}_{\mathsf{AK}}(\mathsf{C}, \tau ) = 1\end{pmatrix}\\ \perp &{} \hbox { otherwise}. \end{array}\right. }\)
Correctness : Similar to the correctness of construction of 4.2.
Theorem 2
Let \((\mathcal {T}_1, \mathcal {T}_2, \mathcal {T}_3)\) be a verifiability-friendly index-transformer, \(\mathsf{PE}'\) be an IND-CPA secure predicate encryption scheme with verifiability-1, \((\mathsf{Mac}, \mathsf{MVer})\) and \((\mathsf{wCSetup}, \mathsf{wCommit}, \mathsf{wDecommit})\) respectively be the secure MAC and weak commitment scheme. Then the above proposed scheme \(\mathsf{PE}\) in “Appendix D” is an IND-CCA secure predicate encryption scheme.
Proof
The proof is similar to the proof of Theorem 1 in Sect. 4.2, but for avoiding circularity from primitive predicate encryption and weak commitment, the arguments of [10] are used. For the sake of completeness, we provide here a proof in details using the proof strategy of [10]. Let \(\mathsf{CT}^*= (\mathsf{C}^*, \tau ^*, \mathsf{vk}^*)\) denote the challenge ciphertext, where \(\mathsf{C}^*\longleftarrow \mathsf{Encrypt}'(m_b||\mathsf{decom}^*, y^*_{\mathsf{vk}^*})\), \(\tau ^*\longleftarrow \mathsf{Mac}_{\mathsf{AK}^*}(\mathsf{C}^*)\), \((\mathsf{AK}^*,\mathsf{vk}^*,\mathsf{decom}^*)\longleftarrow \mathsf{wCommit}(\mathsf{pub})\) and \(b\mathop {\longleftarrow }\limits ^{\mathrm {U}}\{0,1\}\). Let \(\mathsf{E}\) be an event that \(\mathscr {A}\) ever submits a decrypt query of the form \((\mathsf{CT}= (\mathsf{C},\tau ,\mathsf{vk}^*), x)\) for which (a) \(m||\mathsf{decom}\longleftarrow \mathsf{Decrypt}'(\mathsf{C},{\mathcal {SK}}'_{x'})\) and (b) \(\mathsf{AK}\longleftarrow \mathsf{wDecommit}(\mathsf{pub},\mathsf{vk}^*, \mathsf{decom})\) with \(\mathsf{AK}\not \in \{\mathsf{AK}^*,\perp \}\). Based on the event \(\mathsf{E}\), we define the following games.
-
\(\mathrm {Game}_{Real}\) : The original IND-CCA game of the encryption scheme \(\mathsf{PE}\).
-
\(\mathrm {Game}_{0}\) : Same as \(\mathrm {Game}_{Real}\), except when a decrypt query satisfies the event \(\mathsf{E}\), the challenger always returns \(\perp \) to the adversary \(\mathscr {A}\).
Let \(\mathsf{F}\) be the event that \(\mathsf{E}\) does not happen and at some point \(\mathscr {A}\) submits a decrypt query of the form \((\mathsf{CT}= (\mathsf{C},\tau ,\mathsf{vk}^*), x)\) such that \(\mathsf{MVer}_{\mathsf{AK}^*}(\mathsf{C}, \tau ) = 1\).
Using Lemma 1 and Lemma 2, we have:
where \(\Pr _0[\mathsf{F}]\) is the probability of the event \(\mathsf{F}\) in \(\mathrm {Game}_{0}\), \(\mathsf{Adv}_{\mathscr {A}, \mathrm{PE}}^\mathrm{j} (\kappa )\) is the advantage of win in \(\mathrm {Game}_j\) for \(i\in \{0, \text {Real}\}\), and \(\mathscr {B}_0\) and \(\mathscr {B}_1\) are PPT algorithms whose running times are same as that of \(\mathscr {A}\).
Now it is sufficient to show that \(\Pr _0[\mathsf{F}]\) is negligible. Let \(\nu \) be the maximum number of decrypt queries. Let \(\mathsf{F}_i\) be the event that the event \(\mathsf{F}\) occurs first time at \(i^{th}\) decrypt query. Let \(\mathsf{F}'_i\) be the event that the \(i^{th}\) decrypt query is of the form \((\mathsf{CT}= (\mathsf{C}, \tau , \mathsf{vk}^*),x)\) and \(\mathsf{MVer}_{\mathsf{AK}^*}(\mathsf{C},\tau ) = 1\) when all the previous queries have the form \((\mathsf{CT}= (\mathsf{C}', \tau ', \mathsf{vk}^*),x)\) and are answered with \(\perp \) without checking whether they are valid or not. Let the later game be called \(\mathrm {Game}_{0'}\). We note that \(\Pr _0[\mathsf{F}]\) is same as \(\sum _{i=1}^\nu \Pr _{0}[\mathsf{F}_i]\). Let \(\Pr _{0'}[\mathsf{F}'] := \sum _{i=1}^\nu \Pr _{0'}[\mathsf{F}'_i]\). Since for all \(i\in [\nu ]\), \(\Pr _{0}[\mathsf{F}_i]\le \Pr _{0'}[\mathsf{F}'_i]\), we have \(\Pr _{0}[\mathsf{F}]\le \Pr _{0'}[\mathsf{F}']\). To bound the probability \(\Pr _{0'}[\mathsf{F}']\), we define the following games.
-
\(\mathrm {Game}_{1}\) : Same as \(\mathrm {Game}_{0'}\) except the part of challenge ciphertext construction, i.e., \(\mathsf{C}^*\longleftarrow \mathsf{Encrypt}'(m_b||0^{\ell (\kappa )})\), where \(\ell (\kappa )\) is the length of \(\mathsf{decom}\).
-
\(\mathrm {Game}_{2}\) : Same as \(\mathrm {Game}_{1}\), except the part of challenge ciphertext construction, i.e., \(\tau ^*\longleftarrow \mathsf{Mac}_{\mathsf{AK}^*}(\mathsf{C}^*)\), where \(\mathsf{AK}^*\mathop {\longleftarrow }\limits ^{\mathrm {U}}\{0,1\}^{\kappa }\) (independent of \(\mathsf{vk}^*\)).
Using Lemma 3, Lemma 4 and Lemma 5, we have
where \(\mathscr {B}_2\), \(\mathscr {B}_3\) and \(\mathscr {B}_4\) are PPT algorithms whose running times are same as that of \(\mathscr {A}\). This concludes the theorem. \(\square \)
The following lemmas can be proven in straightforward manner.
Lemma 1
\(\mathrm {Game}_{Real}\) and \(\mathrm {Game}_0\) are indistinguishable under the binding property of the weak commitment scheme. That is, for any adversary \(\mathscr {A}\), there is a PPT algorithm \(\mathscr {B}\) such that
Lemma 2
For any adversary \(\mathscr {A}\), there is a PPT algorithm \(\mathscr {B}\) such that
Lemma 3
For any adversary \(\mathscr {A}\), there is a PPT algorithm \(\mathscr {B}\) such that
Lemma 4
For any adversary \(\mathscr {A}\), there is a PPT algorithm \(\mathscr {B}\) such that
Lemma 5
For any adversary \(\mathscr {A}\), there is a PPT algorithm \(\mathscr {B}\) such that
E A concrete fully CCA-secure construction based on Attrapadung’s scheme
In this section, we provide a fully CCA-secure FE scheme for regular languages using MAC and weak commitment scheme. We consider the fully CPA-secure FE scheme of [1] for regular languages as the primitive predicate encryption scheme. This scheme is constructed from Pair Encoding Scheme 7 of [1]. The primitive CPA-secure scheme possesses verifiability-1 as shown in [25]. The algorithm Verify found in Decrypt algorithm is a part of verifiability-1. W.l.o.g, we assume that the input DFA to the encryption algorithm has a single final state, i.e., \({M}= (Q,\varSigma ,\mathsf{Tr}, q_0,F := \{q_f\})\). To maintain this form of DFA under the transformation \(\mathcal {T}_3\), we slightly modify \({M}_{\mathsf{vk}} := \mathcal {T}_3({M},\mathsf{vk})\) which will be found in the Encrypt algorithm given below.
-
\(\mathsf{Setup}(1^\kappa ):\) It runs \(\mathcal {J}:= (N := p_{1}p_{2}p_{3},\mathbb {G},\>,e) \longleftarrow \mathcal {G}_{\mathsf{cbg}}(1^{\kappa })\). It chooses \(g\mathop {\longleftarrow }\limits ^{\mathrm {U}}\mathbb {G}_{p_1}, Z_{3}\mathop {\longleftarrow }\limits ^{\mathrm {U}}\mathbb {G}_{p_3}\). It then chooses \(h_0,\ldots ,h_4\), \(\phi _1,\phi _2,\phi _3\), \(\eta \), \(\alpha \mathop {\longleftarrow }\limits ^{\mathrm {U}}{\mathbb {Z}_{N}}\). Let n be an integer related to the security parameter \(\kappa \) which would be chosen so that the security advantages contributed by n is comparable to other security components of security advantages. Let \(\mathbb {F}_{2^n}\) denote the finite field of size \(2^n\). It chooses \(K_0, K_1, K_2 \mathop {\longleftarrow }\limits ^{\mathrm {U}} \mathbb {F}_{2^{2n}}\). Moreover, we fix a collision resistant hash function \(H: \{0,1\}^{*} \rightarrow \{0,1\}^n\). It chooses an alphabet \(\varSigma \) to be any subset of \({\mathbb {Z}_{N}}\). W.l.o.g, we assume that \(0,1\not \in \varSigma \) and set \(\varSigma ' := \varSigma \cup \{0,1\}\). The public parameters and master secret key are given by \({\mathcal {PP}}:= [\mathcal {J}, \varSigma ', g, g^{h_0},\ldots ,g^{h_4},g^{\phi _1},g^{\phi _2},g^{\phi _3}, g^{\eta }, g_T^\alpha := e(g,g)^\alpha , Z_3, K_0, K_1, K_2,H]\), \({\mathcal {MSK}}:= [\alpha ]\).
-
\(\mathsf{KeyGen}({\mathcal {PP}}, {\mathcal {MSK}}, {w}:= w_1\ldots w_{\ell }):\) Here \({w}' = \mathcal {T}_1({w}) := {w}\). It chooses r, u, \(r_0,\ldots ,r_{\ell }\mathop {\longleftarrow }\limits ^{\mathrm {U}}{\mathbb {Z}_{N}}\). Then, picks \(R_1,\ldots ,R_5,R_{6,0}\mathop {\longleftarrow }\limits ^{\mathrm {U}}\mathbb {G}_{p_3}\) and \(R_{6,i}, R_{7,i}\mathop {\longleftarrow }\limits ^{\mathrm {U}}\mathbb {G}_{p_3}\) for \(i\in [\ell ]\). It first computes the initial key components
$$\begin{aligned} K_1 := g^{\alpha +r\phi _1+u\eta }\cdot R_1,\ K_2 := g^u\cdot R_2,\ K_3 := g^r\cdot R_3, K_4 := g^{-r\phi _2 + r_{\ell }\phi _3}\cdot R_4, \end{aligned}$$$$\begin{aligned} K_5 := g^{r_0h_0}\cdot R_5,\ K_{6,0} := g^{r_0}\cdot R_{6,0}. \end{aligned}$$Then, for \(i\in [\ell ]\), it computes
$$\begin{aligned} K_{6,i} := g^{r_i}\cdot R_{6,i},\ K_{7,i} := g^{r_{i-1}(h_1 + h_2w_i) + r_i(h_3 + h_4w_i)}\cdot R_{7,i}. \end{aligned}$$It returns the secret key
$$\begin{aligned} {\mathcal {SK}}_{{w}'} := [{w}, K_1, K_2, K_3,K_4, K_5, K_{6,0}, \{K_{6,i},K_{7,i}\}_{i\in [\ell ]}]. \end{aligned}$$
-
\(\mathsf{Encrypt}({\mathcal {PP}}, m, {M}:= (Q,\varSigma ,\mathsf{Tr}, q_0,F := \{q_f\})):\) It first chooses \(\mathsf{decom}:= (d_1, d_2)\) \(\mathop {\longleftarrow }\limits ^{\mathrm {U}} \mathbb {F}_{2^{2n}}^2\) and defines \(\mathsf{vk}= H(d_1, d_2)\). Then, computes \(\textsf {AK} = K_0 + K_1d_1 + K_2d_2\) and writes it as \((\widetilde{r}_1, \widetilde{r}_2) \in \mathbb {F}_{2^n}^2\). Then, it applies the transformation \(\mathcal {T}_3\) on \({M}\) and let \(\mathcal {T}_3({M},\mathsf{vk}) = {M}_{\mathsf{vk}} := (Q', \varSigma ', q'_0, \mathsf{Tr}',F)\), where \(q'_0 := q_0\), \(Q' := Q\cup \{q'_1,\ldots ,q'_{n-1}\}\) with \(q'_1,\ldots ,q'_{n-1}\not \in Q\), \(q'_n := q_f\) and \(\mathsf{Tr}' := \mathsf{Tr}\cup \{(q'_{i-1}, q'_i,\mathsf{vk}[i]) : i\in [n]\}\). Let \(\tau := |\mathsf{Tr}'|\). It picks \(s,v,s_0,\ldots ,s_{\tau }\mathop {\longleftarrow }\limits ^{\mathrm {U}}{\mathbb {Z}_{N}}\). Then, chooses \(u_x\mathop {\longleftarrow }\limits ^{\mathrm {U}}{\mathbb {Z}_{N}}\) for \(q_x\in Q'{\setminus }\{q_f\}\) and for the final state \(q_f\), it sets \(u_f := v\phi _3\). The initial components of the key are computed as
$$\begin{aligned} C_0 := (m||\mathsf{decom})\cdot g^{\alpha s}_T,\ C_1 := g^s,\ C_2 := g^{s\eta },\ C_3 := g^{s\phi _1 + v\phi _2}, \\ C_4 := g^v,\ C_5 := g^{s_0},\ C_6 := g^{-u_0 + s_0h_0}. \end{aligned}$$For each transition \(t := (q_{x_t},q_{y_t},\sigma _t)\in \mathsf{Tr}'\), it computes the key components
$$\begin{aligned} C_{7,t} := g^{s_t},\ C_{8,t} := g^{u_{x_t} + s_t(h_1 + h_2\sigma _t)},\ C_{9,t} := g^{-u_{y_t} + s_t(h_3 + h_4\sigma _t)}. \end{aligned}$$It sets \(C_{{M}_{\mathsf{vk}}} := [{M}_{\mathsf{vk}}, C_0, C_1, C_2, C_3, C_4, C_5, C_6, \{C_{7,t}, C_{8,t}, C_{9,t}\}_{t\in \mathsf{Tr}'}]\) and returns the ciphertext \(\mathsf{CT}_{{M}} := (C_{{M}_{\mathsf{vk}}}, \tau , \mathsf{vk})\), where \(\tau := \widetilde{r}_1H(C_{{M}_{\mathsf{vk}}}) + \widetilde{r}_2\).
-
\(\mathsf{Decrypt}({\mathcal {PP}}, \mathsf{CT}_{{M}} := (C_{{M}_{\mathsf{vk}}}, \tau , \mathsf{vk}), {\mathcal {SK}}_{{w}'}):\) It sets \(\mathcal {T}_2(\mathsf{vk}) = \epsilon _{\mathsf{vk}} := \mathsf{vk}\). Let \({w}' = {w}:= w_1\ldots w_{\ell }\). If
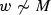 or \(\mathsf{Verify}({\mathcal {PP}},C_{{M}_{\mathsf{vk}}},{w}',\epsilon _{\mathsf{vk}})\ne 1\), returns \(\perp \). Otherwise, performs the following steps. Since, \({M}\) accepts \({w}\), so \({M}_{\mathsf{vk}}\) accepts \({w}\). Therefore, there exist a sequence of states, \(\rho _0,\ldots ,\rho _{\ell }\in Q'\) and \(\ell \) transitions \(t_1,\ldots ,t_{\ell }\in \mathsf{Tr}'\) such that \(\rho _0 = q_0\) and \(\rho _{\ell } = q_f\), where \(t_i := (q_{x_{t_i}},q_{y_{t_i}},\sigma _{t_i}) = (\rho _{i-1},\rho _i,w_i)\) for \(i\in [\ell ]\). As a basic step, it first computes $$\begin{aligned} B_0&:= e(C_1,K_1)^{-1}\cdot e(C_2,K_2)\cdot e(C_3,K_3)\cdot e(C_4,K_4)\cdot e(C_5,K_5) ^{-1}\cdot e(C_6,K_{6,0})\\&= g^{-\alpha s- r_0u_0 + r_\ell v\phi _3}_T = g^{-\alpha s- r_0u_0 + r_\ell u_f}_T. \end{aligned}$$
or \(\mathsf{Verify}({\mathcal {PP}},C_{{M}_{\mathsf{vk}}},{w}',\epsilon _{\mathsf{vk}})\ne 1\), returns \(\perp \). Otherwise, performs the following steps. Since, \({M}\) accepts \({w}\), so \({M}_{\mathsf{vk}}\) accepts \({w}\). Therefore, there exist a sequence of states, \(\rho _0,\ldots ,\rho _{\ell }\in Q'\) and \(\ell \) transitions \(t_1,\ldots ,t_{\ell }\in \mathsf{Tr}'\) such that \(\rho _0 = q_0\) and \(\rho _{\ell } = q_f\), where \(t_i := (q_{x_{t_i}},q_{y_{t_i}},\sigma _{t_i}) = (\rho _{i-1},\rho _i,w_i)\) for \(i\in [\ell ]\). As a basic step, it first computes $$\begin{aligned} B_0&:= e(C_1,K_1)^{-1}\cdot e(C_2,K_2)\cdot e(C_3,K_3)\cdot e(C_4,K_4)\cdot e(C_5,K_5) ^{-1}\cdot e(C_6,K_{6,0})\\&= g^{-\alpha s- r_0u_0 + r_\ell v\phi _3}_T = g^{-\alpha s- r_0u_0 + r_\ell u_f}_T. \end{aligned}$$For each \(i\in [\ell ]\), it computes
$$\begin{aligned} B_i := e(C_{7,t_i}, K_{7,i})^{-1}\cdot e(C_{8,t_i},K_{6,i-1})\cdot e(C_{9,t_i},K_{6,i}) = g^{u_{x_{t_i}}r_{i-1} - u_{y_{t_i}}r_i}_T. \end{aligned}$$Then, computes \(B := B_0\prod _{i=1}^{\ell }B_i\). Let \(m||\mathsf{decom}= B\cdot C_0\) and write \(\mathsf{decom}\) as \((d_1,d_2)\). It checks \(H(d_1,d_2)\mathop {=}\limits ^{\mathrm {?}}\mathsf{vk}\). If the equality does not hold, it returns \(\perp \). Then, computes \(\textsf {AK} = (r_1,r_2) := K_0 + K_1d_1 + K_2d_2\). It returns \(m\) if \(\tau = \widetilde{r}_1H(\mathsf{C}_{{w}_{\mathsf{vk}}}) + \widetilde{r}_2\) else \(\perp \).
Discussion. In the above construction, we instantiate the weak commitment by the commitment scheme of [21] using the pair-wise independent hash \(K_0 + K_1d_1 + K_2d_2\) and the collision resistant function H. The function \(\widetilde{r}_1H + \widetilde{r}_2\) plays the role of one-time MAC.
Theorem 3
Let H be a collision resistant hash function. Suppose the \(\ell ^*\)-EDHE1-Dual assumption [1] and the \((n^{*}+n-1, \tau ^*+n)\)-EDHE2-Dual assumption [1] hold, where \(\ell ^*\) is the maximum length of phase 1 query strings, \({M}^*:= (Q^*,\varSigma ,\mathsf{Tr}^*, q^*_0,F^*:= \{q^*_f\})\) is the challenge DFA with \(n^*:= |Q^{*}|\) and \(\tau ^*:= |\mathsf{Tr}^*|\). Then the above construction is adaptive-predicate IND-CCA-secure CP-FE for regular languages.
Proof
It is followed from the proof of Theorem 2 in Sect. D and Theorem 1, Theorem 19 and Theorem 20 of [1]. We note that Theorem 1, Theorem 19 and Theorem 20 of [1] are used to prove the IND-CPA security of the primitive CP-FE scheme for regular languages in adaptive-predicate model. \(\square \)
Remark 1
The KP-FE scheme of Waters [35] for regular languages can be shown to have verifiability-1 by the arguments of [25]. This scheme was shown to be selectively CPA-secure under \(\ell ^*\)-Expanded BDHE assumption, where \(\ell ^*\) is the size of the challenge string \({w}^*\). By applying our conversion, we can get selectively CCA-secure KP-FE scheme for regular languages, which relies on \((\ell ^*+n)\)-Expanded BDHE assumption [35].
Rights and permissions
About this article
Cite this article
Nandi, M., Pandit, T. Verifiability-based conversion from CPA to CCA-secure predicate encryption. AAECC 29, 77–102 (2018). https://doi.org/10.1007/s00200-017-0330-2
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00200-017-0330-2





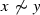 , the simulator always returns
, the simulator always returns 

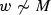 or
or