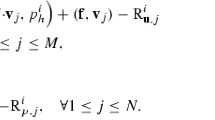An adaptive least-squares FEM for the Stokes equations with optimal convergence rates

Abstract

This paper introduces the first adaptive least-squares finite element method (LS-FEM) for the Stokes equations with optimal convergence rates based on the newest vertex bisection with lowest-order Raviart-Thomas and conforming $P_1$ discrete spaces for the divergence least-squares formulation in 2D. Although the least-squares functional is a reliable and efficient error estimator, the novel refinement indicator stems from an alternative explicit residual-based a posteriori error control with exact solve. Particular interest is on the treatment of the data approximation error which requires a separate marking strategy. The paper proves linear convergence in terms of the levels and optimal convergence rates in terms of the number of unknowns relative to the notion of a non-linear approximation class. It extends and generalizes the approach of Carstensen and Park (SIAM J. Numer. Anal. 53:43–62 2015) from the Poisson model problem to the Stokes equations.

Appendix: Proofs of Lemma 4.5–4.7

Proof

(Proof of Lemma 4.5) For g replaced by $\widehat{I} g \in S^{1}(\widehat{\mathcal {E}}({\Gamma });{\mathbb {R}}^2)$, Lemma 2.1 guarantees the existence of some $\widehat{z}\in S^{1}(\widehat{\mathcal {T}};{\mathbb {R}}^2)$ with

$$\begin{aligned} \widehat{z}\vert _{\Gamma }=(\widehat{I} - I)g \quad \text {and}\quad \big \vert \!\big \vert \!\big \vert \widehat{z} \big \vert \!\big \vert \!\big \vert \lesssim {{\mathrm{osc}}}(\widehat{\Pi } g',\mathcal {E}({\Gamma })). \end{aligned}$$

The discrete equation (11) with respect to $\widehat{\mathcal {T}}$ with test functions ${\varvec{\tau }}_{\mathrm{LS}}= \widehat{{\varvec{\sigma }}}_{\mathrm{LS}}-{\varvec{\sigma }}_{\mathrm{LS}}\in {\varvec{\Sigma }}(\widehat{\mathcal {T}})$ and $v_{\mathrm{LS}}= \widehat{u}_{\mathrm{LS}}-u_{\mathrm{LS}}-\widehat{z}\in S^{1}_0(\widehat{\mathcal {T}};{\mathbb {R}}^2)$ imply that

$$\begin{aligned}&-\int _\Omega ({{\mathrm{dev}}}\widehat{{\varvec{\sigma }}}_{\mathrm{LS}}-{{\mathrm{D}}}\widehat{u}_{\mathrm{LS}}) : ({{\mathrm{dev}}}(\widehat{{\varvec{\sigma }}}_{\mathrm{LS}}-{\varvec{\sigma }}_{\mathrm{LS}})-{{\mathrm{D}}}(\widehat{u}_{\mathrm{LS}}-u_{\mathrm{LS}}-\widehat{z})) \mathrm{d} x\\&\quad =\int _\Omega (f_{\widehat{\mathcal {T}}} + {{\mathrm{div}}}\widehat{{\varvec{\sigma }}}_{\mathrm{LS}}) \cdot {{\mathrm{div}}}(\widehat{{\varvec{\sigma }}}_{\mathrm{LS}}-{\varvec{\sigma }}_{\mathrm{LS}})\mathrm{d} x\\&\quad =\int _\Omega (f_{\widehat{\mathcal {T}}}-f_\mathcal {T}) \cdot {{\mathrm{div}}}(\widehat{{\varvec{\sigma }}}_{\mathrm{LS}}-{\varvec{\sigma }}_{\mathrm{LS}}) \mathrm{d} x\\&\qquad + \int _\Omega (f_\mathcal {T}+{{\mathrm{div}}}{\varvec{\sigma }}_{\mathrm{LS}}) \cdot {{\mathrm{div}}}(\widehat{{\varvec{\sigma }}}_{\mathrm{LS}}-{\varvec{\sigma }}_{\mathrm{LS}}) \mathrm{d} x+\big \Vert {{\mathrm{div}}}(\widehat{{\varvec{\sigma }}}_{\mathrm{LS}}-{\varvec{\sigma }}_{\mathrm{LS}})\big \Vert _{L^{2}({\Omega })}^2. \end{aligned}$$

The discrete equation (11) with respect to ${\varvec{\tau }}_{\mathrm{LS}}= {\varvec{\tau }}_{\mathrm{PS}}$ and the triangulation $\mathcal {T}$ and (21) result in

$$\begin{aligned}&-\int _\Omega ({{\mathrm{dev}}}{\varvec{\sigma }}_{\mathrm{LS}}-{{\mathrm{D}}}u_{\mathrm{LS}}) : {{\mathrm{dev}}}{\varvec{\tau }}_{\mathrm{PS}}\mathrm{d} x\\&\quad =\int _\Omega (f_\mathcal {T}+{{\mathrm{div}}}{\varvec{\sigma }}_{\mathrm{LS}}) \cdot {{\mathrm{div}}}{\varvec{\tau }}_{\mathrm{PS}}\mathrm{d} x=\int _\Omega (f_\mathcal {T}+{{\mathrm{div}}}{\varvec{\sigma }}_{\mathrm{LS}}) \cdot {{\mathrm{div}}}(\widehat{{\varvec{\sigma }}}_{\mathrm{LS}}-{\varvec{\sigma }}_{\mathrm{LS}}) \mathrm{d} x. \end{aligned}$$

The combination of the preceding two displayed formulas proves

$$\begin{aligned}&\big \Vert {{\mathrm{div}}}(\widehat{{\varvec{\sigma }}}_{\mathrm{LS}}-{\varvec{\sigma }}_{\mathrm{LS}})\big \Vert _{L^{2}({\Omega })}^2\\&\quad =-\int _\Omega (f_{\widehat{\mathcal {T}}}-f_\mathcal {T}) \cdot {{\mathrm{div}}}(\widehat{{\varvec{\sigma }}}_{\mathrm{LS}}-{\varvec{\sigma }}_{\mathrm{LS}}) \mathrm{d} x+ \int _\Omega ({{\mathrm{dev}}}{\varvec{\sigma }}_{\mathrm{LS}}- {{\mathrm{D}}}u_{\mathrm{LS}}) : {{\mathrm{dev}}}{\varvec{\tau }}_{\mathrm{PS}}\mathrm{d} x\\&\qquad - \int _\Omega ({{\mathrm{dev}}}\widehat{{\varvec{\sigma }}}_{\mathrm{LS}}-{{\mathrm{D}}}\widehat{u}_{\mathrm{LS}}) : \big ({{\mathrm{dev}}}(\widehat{{\varvec{\sigma }}}_{\mathrm{LS}}-{\varvec{\sigma }}_{\mathrm{LS}}) -{{\mathrm{D}}}(\widehat{u}_{\mathrm{LS}}-u_{\mathrm{LS}}-\widehat{z})\big ) \mathrm{d} x. \end{aligned}$$

This plus some elementary algebra leads to

$$\begin{aligned}&\big \Vert {{\mathrm{div}}}(\widehat{{\varvec{\sigma }}}_{\mathrm{LS}}-{\varvec{\sigma }}_{\mathrm{LS}})\big \Vert _{L^{2}({\Omega })}^2 + \big \Vert {{\mathrm{dev}}}(\widehat{{\varvec{\sigma }}}_{\mathrm{LS}}-{\varvec{\sigma }}_{\mathrm{LS}})-{{\mathrm{D}}}(\widehat{u}_{\mathrm{LS}}-u_{\mathrm{LS}})\big \Vert _{L^{2}({\Omega })}^2\nonumber \\&=-\int _\Omega (f_{\widehat{\mathcal {T}}}-f_\mathcal {T}) \cdot {{\mathrm{div}}}(\widehat{{\varvec{\sigma }}}_{\mathrm{LS}}-{\varvec{\sigma }}_{\mathrm{LS}})\mathrm{d} x\nonumber \\&\quad -\int _\Omega ({{\mathrm{dev}}}{\varvec{\sigma }}_{\mathrm{LS}}- {{\mathrm{D}}}u_{\mathrm{LS}}) : \big ({{\mathrm{dev}}}(\widehat{{\varvec{\sigma }}}_{\mathrm{LS}}-{\varvec{\sigma }}_{\mathrm{LS}}-{\varvec{\tau }}_{\mathrm{PS}}) -{{\mathrm{D}}}(\widehat{u}_{\mathrm{LS}}-u_{\mathrm{LS}}-\widehat{z}) \big ) \mathrm{d} x\nonumber \\&\quad -\int _\Omega ({{\mathrm{dev}}}(\widehat{{\varvec{\sigma }}}_{\mathrm{LS}}-{\varvec{\sigma }}_{\mathrm{LS}})-{{\mathrm{D}}}(\widehat{u}_{\mathrm{LS}}-u_{\mathrm{LS}})) : {{\mathrm{D}}}\widehat{z} \mathrm{d} x. \end{aligned}$$

(43)

The remaining analysis in this proof concerns the split

$$\begin{aligned} {{\mathrm{dev}}}(\widehat{{\varvec{\sigma }}}_{\mathrm{LS}}-{\varvec{\sigma }}_{\mathrm{LS}}-{\varvec{\tau }}_{\mathrm{PS}}) = {{\mathrm{dev}}}(\widehat{{\varvec{\sigma }}}_{\mathrm{LS}}-{\varvec{\sigma }}_{\mathrm{LS}}-\widehat{{\varvec{\tau }}}_{\mathrm{PS}}+\widehat{{\varvec{\tau }}}_{\mathrm{PS}}^*-{\varvec{\tau }}_{\mathrm{PS}}) + {{\mathrm{dev}}}(\widehat{{\varvec{\tau }}}_{\mathrm{PS}}-\widehat{{\varvec{\tau }}}_{\mathrm{PS}}^*). \end{aligned}$$

The Eq. (21) imply that the Raviart-Thomas function

$$\begin{aligned} \widehat{\varvec{\rho }} := \widehat{{\varvec{\sigma }}}_{\mathrm{LS}}-{\varvec{\sigma }}_{\mathrm{LS}}-\widehat{{\varvec{\tau }}}_{\mathrm{PS}}+\widehat{{\varvec{\tau }}}_{\mathrm{PS}}^*-{\varvec{\tau }}_{\mathrm{PS}}\end{aligned}$$

(44)

is divergence-free and so piecewise constant. The Helmholtz decomposition (14),

$$\begin{aligned} {{\mathrm{dev}}}\widehat{\varvec{\rho }} = {{\mathrm{{{\mathrm{D}}}_{{\mathrm{NC}}}}}}\widehat{\alpha } + {{\mathrm{dev}}}{{\mathrm{Curl}}}\widehat{\beta } \in P_0(\widehat{\mathcal {T}};{\mathbb {R}}^{2\times 2}_{{{\mathrm{dev}}}}), \end{aligned}$$

leads to some $\widehat{\alpha }\in Z(\widehat{\mathcal {T}})$ and $\widehat{\beta }\in X(\widehat{\mathcal {T}})$. The orthogonality and a piecewise integration by parts show

$$\begin{aligned} \big \vert \!\big \vert \!\big \vert \widehat{\alpha } \big \vert \!\big \vert \!\big \vert _{\mathrm{NC}}^2 =\int _\Omega {{\mathrm{dev}}}\widehat{\varvec{\rho }} : {{\mathrm{{{\mathrm{D}}}_{{\mathrm{NC}}}}}}\widehat{\alpha } \mathrm{d} x= \int _\Omega \widehat{\varvec{\rho }}:{{\mathrm{{{\mathrm{D}}}_{{\mathrm{NC}}}}}}\widehat{\alpha } \mathrm{d} x=\sum _{E\in \widehat{\mathcal {E}}(\Omega )} \int _E [\widehat{\varvec{\rho }}\nu _E \cdot \widehat{\alpha } ]_E \, \mathrm {d} s. \end{aligned}$$

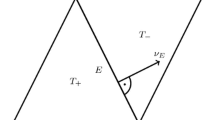
Recall that the Raviart-Thomas function $\widehat{\varvec{\rho }}$ is continuous in its normal components and that $\widehat{\varvec{\rho }}\nu _E$ is constant along $E\in \widehat{\mathcal {E}}(\Omega )$. Since the jump $[\widehat{\alpha } ]_E$ of E has integral mean zero along E,

$$\begin{aligned} \int _E [\widehat{\varvec{\rho }}\nu _E \cdot \widehat{\alpha } ]_E \, \mathrm {d} s=0. \end{aligned}$$

Hence, $\widehat{\alpha }\equiv 0$ and the Helmholtz decomposition reduces to

$$\begin{aligned} {{\mathrm{dev}}}\widehat{\varvec{\rho }} = {{\mathrm{dev}}}{{\mathrm{Curl}}}\widehat{\beta } \end{aligned}$$

(45)

for the divergence-free test function ${{\mathrm{Curl}}}\widehat{\beta } \in RT_0(\widehat{\mathcal {T}};\mathbb {R}^{2 \times 2})$. One term in (43) reads

$$\begin{aligned}&-\int _\Omega ({{\mathrm{dev}}}{\varvec{\sigma }}_{\mathrm{LS}}- {{\mathrm{D}}}u_{\mathrm{LS}}) : {{\mathrm{dev}}}(\widehat{{\varvec{\tau }}}_{\mathrm{PS}}-\widehat{{\varvec{\tau }}}_{\mathrm{PS}}^*)\mathrm{d} x\nonumber \\&\quad =\int _\Omega ({{\mathrm{dev}}}(\widehat{{\varvec{\sigma }}}_{\mathrm{LS}}-{\varvec{\sigma }}_{\mathrm{LS}})-{{\mathrm{D}}}(\widehat{u}_{\mathrm{LS}}-u_{\mathrm{LS}})) : {{\mathrm{dev}}}(\widehat{{\varvec{\tau }}}_{\mathrm{PS}}-\widehat{{\varvec{\tau }}}_{\mathrm{PS}}^*) \mathrm{d} x\nonumber \\&\qquad -\int _\Omega ({{\mathrm{dev}}}\widehat{{\varvec{\sigma }}}_{\mathrm{LS}}-{{\mathrm{D}}}\widehat{u}_{\mathrm{LS}}) : {{\mathrm{dev}}}(\widehat{{\varvec{\tau }}}_{\mathrm{PS}}-\widehat{{\varvec{\tau }}}_{\mathrm{PS}}^*)\mathrm{d} x. \end{aligned}$$

(46)

The discrete equation (11) with respect to the triangulation $\widehat{\mathcal {T}}$, ${\varvec{\tau }}_{\mathrm{LS}}=\widehat{{\varvec{\tau }}}_{\mathrm{PS}}-\widehat{{\varvec{\tau }}}_{\mathrm{PS}}^*$, and $v_{\mathrm{LS}}\equiv 0$, and the combination with (21) plus elementary algebra with the $L^2$-projection $\Pi$ onto $P_0(\mathcal {T};{\mathbb {R}}^{2\times 2})$ show

$$\begin{aligned}&-\int _\Omega ({{\mathrm{dev}}}\widehat{{\varvec{\sigma }}}_{\mathrm{LS}}-{{\mathrm{D}}}\widehat{u}_{\mathrm{LS}}) : {{\mathrm{dev}}}(\widehat{{\varvec{\tau }}}_{\mathrm{PS}}-\widehat{{\varvec{\tau }}}_{\mathrm{PS}}^*) \mathrm{d} x\nonumber \\&\quad =\int _\Omega (f_{\widehat{\mathcal {T}}} + {{\mathrm{div}}}\widehat{{\varvec{\sigma }}}_{\mathrm{LS}})\cdot {{\mathrm{div}}}(\widehat{{\varvec{\tau }}}_{\mathrm{PS}}-\widehat{{\varvec{\tau }}}_{\mathrm{PS}}^*) \mathrm{d} x\nonumber \\&\quad =\int _\Omega (f_{\widehat{\mathcal {T}}} + {{\mathrm{div}}}\widehat{{\varvec{\sigma }}}_{\mathrm{LS}})\cdot \big ((1-\Pi ){{\mathrm{div}}}(\widehat{{\varvec{\sigma }}}_{\mathrm{LS}}-{\varvec{\sigma }}_{\mathrm{LS}})\big ) \mathrm{d} x\nonumber \\&\quad =\int _\Omega (f_{\widehat{\mathcal {T}}}-f_\mathcal {T}) \cdot {{\mathrm{div}}}(\widehat{{\varvec{\sigma }}}_{\mathrm{LS}}-{\varvec{\sigma }}_{\mathrm{LS}})\mathrm{d} x+ \big \Vert (1-\Pi ){{\mathrm{div}}}(\widehat{{\varvec{\sigma }}}_{\mathrm{LS}}-{\varvec{\sigma }}_{\mathrm{LS}})\big \Vert _{L^{2}({\Omega })}^2. \end{aligned}$$

(47)

The combination of (43)–(47) concludes the proof. $\square$

Proof

(Proof of Lemma 4.6) Let $v \in S^{1}_0(\mathcal {T};{\mathbb {R}}^2)$ be the Scott-Zhang quasi-interpolation of $\widehat{v}:= \widehat{u}_{\mathrm{LS}}-u_{\mathrm{LS}}-\widehat{z} \in S^{1}_0(\widehat{\mathcal {T}};{\mathbb {R}}^2)$. For every $z\in \mathcal {N}$ in the construction of the quasi-interpolation [26, Section 2], choose $E\in \mathcal {E}(\omega _z)$ such that $E\in \mathcal {E}\cap \widehat{\mathcal {E}}$, whenever possible. This ensures that the error function $\widehat{w}:= \widehat{v}-v \in S^{1}_0(\widehat{\mathcal {T}};{\mathbb {R}}^2)$ of the quasi-interpolation vanishes on any $T\in \mathcal {T}\cap \widehat{\mathcal {T}}$. The first-order approximation property [26, equation (4.3)] and the stability property [26, Theorem3.1] read

$$\begin{aligned} \big \vert T \big \vert ^{-1/2}\big \Vert \widehat{w}\big \Vert _{L^{2}({T})} + \big \Vert {{\mathrm{D}}}\widehat{w}\big \Vert _{L^{2}({T})} \lesssim \big \Vert {{\mathrm{D}}}\widehat{v}\big \Vert _{L^{2}({\Omega _T})} \end{aligned}$$

(48)

for the enlarged triangle patch $\Omega _T := \bigcup _{z \in \mathcal {N}(T)} \omega _z$ on the triangulation $\mathcal {T}$ of Fig. 3.

Fig. 3

Enlarged triangle patch $\Omega _T$

Since $v\in S^{1}_0(\mathcal {T};{\mathbb {R}}^2)$ is an admissible test function, (11) implies

$$\begin{aligned} \int _\Omega ({{\mathrm{dev}}}{\varvec{\sigma }}_{\mathrm{LS}}- {{\mathrm{D}}}u_{\mathrm{LS}}) : {{\mathrm{D}}}v \mathrm{d} x= 0. \end{aligned}$$

This, the definition of $\widehat{w}$, and a piecewise integration by parts result in

$$\begin{aligned}&\int _\Omega ({{\mathrm{dev}}}{\varvec{\sigma }}_{\mathrm{LS}}-{{\mathrm{D}}}u_{\mathrm{LS}}):{{\mathrm{D}}}\widehat{v}\mathrm{d} x=\int _\Omega ({{\mathrm{dev}}}{\varvec{\sigma }}_{\mathrm{LS}}-{{\mathrm{D}}}u_{\mathrm{LS}}):{{\mathrm{D}}}\widehat{w}\mathrm{d} x\nonumber \\&\quad =-\sum _{T\in \mathcal {T}{\setminus }\widehat{\mathcal {T}}} \bigg (\int _T \widehat{w} \cdot {{\mathrm{div}}}{{\mathrm{dev}}}{\varvec{\sigma }}_{\mathrm{LS}}\mathrm{d} x\nonumber \\&\qquad +\sum _{E\in \mathcal {E}(T)\cap \mathcal {E}(\Omega )} \int _E \widehat{w}\cdot \big ([{{\mathrm{dev}}}{\varvec{\sigma }}_{\mathrm{LS}}-{{\mathrm{D}}}u_{\mathrm{LS}} ]_{E}\,\nu _E\big )\, \mathrm {d} s\bigg ). \end{aligned}$$

(49)

Given any $T\in \mathcal {T}{\setminus }\widehat{\mathcal {T}}$, a Cauchy-Schwarz inequality plus (48) prove

$$\begin{aligned} \int _T \widehat{w} \cdot {{\mathrm{div}}}{{\mathrm{dev}}}{\varvec{\sigma }}_{\mathrm{LS}}\mathrm{d} x\le&~\big \vert T \big \vert ^{-1/2} \big \Vert \widehat{w}\big \Vert _{L^{2}({T})} \big \vert T \big \vert ^{1/2} \big \Vert {{\mathrm{div}}}{{\mathrm{dev}}}{\varvec{\sigma }}_{\mathrm{LS}}\big \Vert _{L^{2}({T})}\\ \lesssim&~\big \Vert {{\mathrm{D}}}\widehat{v}\big \Vert _{L^{2}({\Omega _T})} \big \vert T \big \vert ^{1/2} \big \Vert {{\mathrm{div}}}{{\mathrm{dev}}}{\varvec{\sigma }}_{\mathrm{LS}}\big \Vert _{L^{2}({T})}. \end{aligned}$$

Given any $T\in \mathcal {T}{\setminus }\widehat{\mathcal {T}}$ with $E\in \mathcal {E}(T)$, a combination of a Cauchy-Schwarz inequality, a trace inequality, and (48) result in

$$\begin{aligned}&\int _E \widehat{w} \cdot \big ([{{\mathrm{dev}}}{\varvec{\sigma }}_{\mathrm{LS}}-{{\mathrm{D}}}u_{\mathrm{LS}} ]_{E}\,\nu _E\big ) \, \mathrm {d} s\\&\quad \le \big \vert T \big \vert ^{-1/4} \big \Vert \widehat{w}\big \Vert _{L^{2}({E})} \big \vert T \big \vert ^{1/4} \big \Vert [{{\mathrm{dev}}}{\varvec{\sigma }}_{\mathrm{LS}}-{{\mathrm{D}}}u_{\mathrm{LS}} ]_{E}\,\nu _E\big \Vert _{L^{2}({E})}\\&\quad \lesssim \big (\big \vert T \big \vert ^{-1/2}\big \Vert \widehat{w}\big \Vert _{L^{2}({T})} + \big \Vert {{\mathrm{D}}}\widehat{w}\big \Vert _{L^{2}({T})}\big ) \big \vert T \big \vert ^{1/4} \big \Vert [{{\mathrm{dev}}}{\varvec{\sigma }}_{\mathrm{LS}}-{{\mathrm{D}}}u_{\mathrm{LS}} ]_{E}\,\nu _E\big \Vert _{L^{2}({E})}\\&\quad \lesssim \big \Vert {{\mathrm{D}}}\widehat{v}\big \Vert _{L^{2}({\Omega _T})} \big \vert T \big \vert ^{1/4} \big \Vert [{{\mathrm{dev}}}{\varvec{\sigma }}_{\mathrm{LS}}-{{\mathrm{D}}}u_{\mathrm{LS}} ]_{E}\,\nu _E\big \Vert _{L^{2}({E})}. \end{aligned}$$

The combination of (49) with the last two preceding estimates and a finite overlap of the patches $\Omega _T$ from Fig. 3 conclude the proof. $\square$

Proof

(Proof of Lemma 4.7) Let $\beta \in S^{1}(\mathcal {T};{\mathbb {R}}^2)$ be the Scott-Zhang quasi-interpolation of $\widehat{\beta }\in S^{1}(\widehat{\mathcal {T}};{\mathbb {R}}^2)$. For every $z\in \mathcal {N}$ in the design of the quasi-interpolation [26, Section 2], choose $E\in \mathcal {E}(\omega _z)$ such that $E\in \mathcal {E}\cap \widehat{\mathcal {E}}$, whenever possible, so that the error function $\widehat{\gamma } := \widehat{\beta } - \beta \in S^{1}(\widehat{\mathcal {T}};{\mathbb {R}}^2)$ of the quasi-interpolation vanishes on any $T\in \mathcal {T}\cap \widehat{\mathcal {T}}$. The first-order approximation property [26, equation (4.3)] and the stability property [26, Theorem 3.1] read, with the enlarged triangle patch $\Omega _T$ of Fig. 3, as

$$\begin{aligned} \big \vert T \big \vert ^{-1/2} \big \Vert \widehat{\gamma }\big \Vert _{L^{2}({T})} +\big \Vert {{\mathrm{D}}}\widehat{\gamma }\big \Vert _{L^{2}({T})} \lesssim \big \Vert {{\mathrm{D}}}\widehat{\beta }\big \Vert _{L^{2}({\Omega _T})}. \end{aligned}$$

(50)

For $x=(x_1,x_2)\in \bar{\Omega }$, define a modified quasi-interpolation $\widetilde{\beta }\in S^{1}(\mathcal {T};{\mathbb {R}}^2)$ by

$$\begin{aligned} \widetilde{\beta }(x) := \beta (x) - c/2\,(-x_2,x_1)^\top \quad \text {with}\quad c := \int _\Omega {{\mathrm{tr}}}{{\mathrm{Curl}}}\beta \mathrm{d} x\Big /\big \vert \Omega \big \vert . \end{aligned}$$

This guarantees that ${{\mathrm{Curl}}}\widetilde{\beta } = {{\mathrm{Curl}}}\beta - c/2\, I_{2\times 2}\in {\varvec{\Sigma }}(\mathcal {T})$ is an admissible and divergence-free test function. Therefore, the discrete equation (11) proves

$$\begin{aligned}&\int _\Omega ({{\mathrm{dev}}}{\varvec{\sigma }}_{\mathrm{LS}}-{{\mathrm{D}}}u_{\mathrm{LS}}) : {{\mathrm{dev}}}{{\mathrm{Curl}}}\beta \mathrm{d} x\\&\quad = \int _\Omega ({{\mathrm{dev}}}{\varvec{\sigma }}_{\mathrm{LS}}-{{\mathrm{D}}}u_{\mathrm{LS}}) : {{\mathrm{dev}}}{{\mathrm{Curl}}}\widetilde{\beta } \mathrm{d} x= 0. \end{aligned}$$

This plus elementary algebra on the deviatoric part and a piecewise integration by parts imply

$$\begin{aligned}&\int _\Omega ({{\mathrm{dev}}}{\varvec{\sigma }}_{\mathrm{LS}}- {{\mathrm{D}}}u_{\mathrm{LS}}) : {{\mathrm{dev}}}{{\mathrm{Curl}}}\widehat{\beta } \mathrm{d} x\\&\quad =\int _\Omega ({{\mathrm{dev}}}{\varvec{\sigma }}_{\mathrm{LS}}- {{\mathrm{D}}}u_{\mathrm{LS}}) : {{\mathrm{dev}}}{{\mathrm{Curl}}}\widehat{\gamma } \mathrm{d} x=\int _\Omega {{\mathrm{dev}}}({\varvec{\sigma }}_{\mathrm{LS}}- {{\mathrm{D}}}u_{\mathrm{LS}}) : {{\mathrm{Curl}}}\widehat{\gamma } \mathrm{d} x\nonumber \\&\quad =-\sum _{T\in \mathcal {T}{\setminus }\widehat{\mathcal {T}}} \bigg (\int _T \widehat{\gamma } \cdot {{\mathrm{curl}}}{{\mathrm{dev}}}({\varvec{\sigma }}_{\mathrm{LS}}-{{\mathrm{D}}}u_{\mathrm{LS}})\mathrm{d} x\nonumber \\&\qquad +\sum _{E\in \mathcal {E}(T)} \int _E \widehat{\gamma } \cdot \big ([{{\mathrm{dev}}}({\varvec{\sigma }}_{\mathrm{LS}}-{{\mathrm{D}}}u_{\mathrm{LS}}) ]_{E} \,\tau _E\big ) \, \mathrm {d} s\bigg ).\nonumber \end{aligned}$$

(51)

Given any $T\in \mathcal {T}{\setminus }\widehat{\mathcal {T}}$, a Cauchy-Schwarz inequality plus (50) prove

$$\begin{aligned} \int _T \widehat{\gamma } \cdot {{\mathrm{curl}}}{{\mathrm{dev}}}{\varvec{\sigma }}_{\mathrm{LS}}\mathrm{d} x\lesssim \big \Vert {{\mathrm{D}}}\widehat{\beta }\big \Vert _{L^{2}({\Omega _T})} \big \vert T \big \vert ^{1/2}\big \Vert {{\mathrm{curl}}}{{\mathrm{dev}}}{\varvec{\sigma }}_{\mathrm{LS}}\big \Vert _{L^{2}({T})}. \end{aligned}$$

Given any $T\in \mathcal {T}{\setminus }\widehat{\mathcal {T}}$ with $E\in \mathcal {E}(T)$, a combination of a Cauchy-Schwarz inequality, a trace inequality, and (50) imply

$$\begin{aligned}&\int _E \widehat{\gamma } \cdot ([{{\mathrm{dev}}}({\varvec{\sigma }}_{\mathrm{LS}}-{{\mathrm{D}}}u_{\mathrm{LS}}) ]_{E}\,\tau _E)\, \mathrm {d} s\\&\quad \le \big \vert T \big \vert ^{-1/4} \big \Vert \widehat{\gamma }\big \Vert _{L^{2}({E})} \big \vert T \big \vert ^{1/4} \big \Vert [{{\mathrm{dev}}}({\varvec{\sigma }}_{\mathrm{LS}}-{{\mathrm{D}}}u_{\mathrm{LS}}) ]_{E} \,\tau _E\big \Vert _{L^{2}({E})}\\&\quad \lesssim \big \Vert {{\mathrm{D}}}\widehat{\beta }\big \Vert _{L^{2}({\Omega _T})} \big \vert T \big \vert ^{1/4} \big \Vert [{{\mathrm{dev}}}({\varvec{\sigma }}_{\mathrm{LS}}-{{\mathrm{D}}}u_{\mathrm{LS}}) ]_{E} \,\tau _E\big \Vert _{L^{2}({E})}. \end{aligned}$$

The combination of (51) with the last two preceding estimates and a finite overlap of the patches $\Omega _T$ from Fig. 3 prove

$$\begin{aligned}&\int _\Omega ({{\mathrm{dev}}}{\varvec{\sigma }}_{\mathrm{LS}}-{{\mathrm{D}}}u_{\mathrm{LS}}):{{\mathrm{dev}}}{{\mathrm{Curl}}}\widehat{\beta }\mathrm{d} x\lesssim \big \vert \!\big \vert \!\big \vert \widehat{\beta } \big \vert \!\big \vert \!\big \vert \bigg (\sum _{T\in \mathcal {T}{\setminus }\widehat{\mathcal {T}}}\Big ( \big \vert T \big \vert \,\big \Vert {{\mathrm{curl}}}{{\mathrm{dev}}}{\varvec{\sigma }}_{\mathrm{LS}}\big \Vert _{L^{2}({T})}^2\nonumber \\&\qquad \qquad +\sum _{E\in \mathcal {E}(T)} \big \vert T \big \vert ^{1/2}\big \Vert [{{\mathrm{dev}}}({\varvec{\sigma }}_{\mathrm{LS}}-{{\mathrm{D}}}u_{\mathrm{LS}}) ]_{E}\, \tau _{E}\big \Vert _{L^{2}({E})}^2 \Big )\bigg )^{1/2}. \end{aligned}$$

(52)

The subsequent stability property can be found in [13, Lemma 3.4] in different notation

$$\begin{aligned} \big \Vert {\varvec{\tau }}_{\mathrm{PS}}\big \Vert _{L^{2}({\Omega })} \lesssim \big \Vert f\big \Vert _{L^{2}({\Omega })}+\big \Vert g\big \Vert _{H^{1/2}({\Gamma })}. \end{aligned}$$

The stability of PS-FEM applied to $\widehat{{\varvec{\tau }}}_{\mathrm{PS}}-\widehat{{\varvec{\tau }}}_{\mathrm{PS}}^*$ and ${\varvec{\tau }}_{\mathrm{PS}}$ yields

$$\begin{aligned} \big \Vert \widehat{{\varvec{\tau }}}_{\mathrm{PS}}-\widehat{{\varvec{\tau }}}_{\mathrm{PS}}^*\big \Vert _{L^{2}({\Omega })}&\lesssim \big \Vert (1-\Pi ){{\mathrm{div}}}(\widehat{{\varvec{\sigma }}}_{\mathrm{LS}}-{\varvec{\sigma }}_{\mathrm{LS}})\big \Vert _{L^{2}({\Omega })} \quad \text {and}\\ \big \Vert {\varvec{\tau }}_{\mathrm{PS}}\big \Vert _{L^{2}({\Omega })}&\lesssim \big \Vert \Pi {{\mathrm{div}}}(\widehat{{\varvec{\sigma }}}_{\mathrm{LS}}-{\varvec{\sigma }}_{\mathrm{LS}})\big \Vert _{L^{2}({\Omega })}.\nonumber \end{aligned}$$

(53)

Since $\widehat{\beta }\in X(\widehat{\mathcal {T}})$, ${{\mathrm{Curl}}}\widehat{\beta } \in \varvec{\Sigma } (\widehat{\mathcal {T}})$. Hence, the tr-dev-div lemma (15), Eq. (45), definition (44), a triangle inequality, and (53) imply

$$\begin{aligned} \big \vert \!\big \vert \!\big \vert \widehat{\beta } \big \vert \!\big \vert \!\big \vert&=\big \Vert {{\mathrm{Curl}}}\widehat{\beta }\big \Vert _{L^{2}({\Omega })} \lesssim \big \Vert {{\mathrm{dev}}}{{\mathrm{Curl}}}\widehat{\beta }\big \Vert _{L^{2}({\Omega })} =\big \Vert {{\mathrm{dev}}}\widehat{\varvec{\rho }}\big \Vert _{L^{2}({\Omega })} \le \big \Vert \widehat{\varvec{\rho }}\big \Vert _{L^{2}({\Omega })}\\&\le \big \Vert \widehat{{\varvec{\sigma }}}_{\mathrm{LS}}-{\varvec{\sigma }}_{\mathrm{LS}}\big \Vert _{L^{2}({\Omega })} +\big \Vert \widehat{{\varvec{\tau }}}_{\mathrm{PS}}-\widehat{{\varvec{\tau }}}_{\mathrm{PS}}^*\big \Vert _{L^{2}({\Omega })} +\big \Vert {\varvec{\tau }}_{\mathrm{PS}}\big \Vert _{L^{2}({\Omega })}\\&\lesssim \big \Vert \widehat{{\varvec{\sigma }}}_{\mathrm{LS}}-{\varvec{\sigma }}_{\mathrm{LS}}\big \Vert _{L^{2}({\Omega })} +\big \Vert (1-\Pi ){{\mathrm{div}}}(\widehat{{\varvec{\sigma }}}_{\mathrm{LS}}-{\varvec{\sigma }}_{\mathrm{LS}})\big \Vert _{L^{2}({\Omega })}\\&\qquad +\big \Vert \Pi {{\mathrm{div}}}(\widehat{{\varvec{\sigma }}}_{\mathrm{LS}}-{\varvec{\sigma }}_{\mathrm{LS}})\big \Vert _{L^{2}({\Omega })}\\&\lesssim \big \Vert \widehat{{\varvec{\sigma }}}_{\mathrm{LS}}-{\varvec{\sigma }}_{\mathrm{LS}}\big \Vert _{H({{\mathrm{div}}},\Omega )}. \end{aligned}$$

This and (52) conclude the proof. $\square$