An Improved Approximation Scheme for Variable-Sized Bin Packing

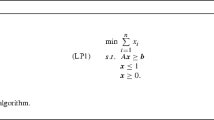
Abstract

The Variable-Sized Bin Packing Problem (abbreviated as VSBPP or VBP) is a well-known generalization of the NP-hard Bin Packing Problem (BP) where the items can be packed in bins of M given sizes. The objective is to minimize the total capacity of the bins used. We present an asymptotic approximation scheme (AFPTAS) for VBP and BP with performance guarantee $A_{\varepsilon }(I) \leq (1+ \varepsilon )OPT(I) + \mathcal {O}\left ({\log ^{2}\left (\frac {1}{\varepsilon }\right )}\right )$ for any problem instance I and any ε>0. The additive term is much smaller than the additive term of already known AFPTAS. The running time of the algorithm is $\mathcal {O}\left ({ \frac {1}{\varepsilon ^{6}} \log \left ({\frac {1}{\varepsilon }}\right ) + \log \left ({\frac {1}{\varepsilon }}\right ) n}\right )$ for BP and $\mathcal {O}\left ({ \frac {1}{{\varepsilon }^{6}} \log ^{2}\left ({\frac {1}{\varepsilon }}\right ) + M + \log \left ({\frac {1}{\varepsilon }}\right )n}\right )$ for VBP, which is an improvement to previously known algorithms. Many approximation algorithms have to solve subproblems, for example instances of the Knapsack Problem (KP) or one of its variants. These subproblems - like KP - are in many cases NP-hard. Our AFPTAS for VBP must in fact solve a generalization of KP, the Knapsack Problem with Inversely Proportional Profits (KPIP). In this problem, one of several knapsack sizes has to be chosen. At the same time, the item profits are inversely proportional to the chosen knapsack size so that the largest knapsack in general does not yield the largest profit. We introduce KPIP in this paper and develop an approximation scheme for KPIP by extending Lawler’s algorithm for KP. Thus, we are able to improve the running time of our AFPTAS for VBP.

Appendices

Appendix A: Solving the LPs Approximately: The Details

We first introduce the max-min resource sharing algorithm by Grigoriadis et al. [12]. Then, the missing proofs of Section 2.4.1 are presented.

1.1 A. 1 Max-Min Resource Sharing

Let $f_{i} : B \rightarrow \mathbb {R}_{\geq 0}$, i=1,…,N, be non-negative concave functions over a non-empty, convex and compact set $B \subset \mathbb {R}^{L}$. The goal is to find λ ^∗:= max{λ| min{f _i (v),i=1,…,N}≥λ,v∈B}, i.e. to solve

$$ \max \lambda \quad \text{ s.t. } \quad f(v) :=\left( \begin{array}{ccc} f_{1}(v) \\ {\vdots} \\ f_{N}(v) \end{array}\right) \geq \lambda\left( \begin{array}{llll}1\\ {\vdots} \\ 1 \end{array}\right), \ v \in B ~~. $$

(48)

This inequality means that every line of the vector f(v) is larger than or equal to λ. Let e:=(1,…,1)^T be the all-1 vector in $\mathbb {R}^{N}$ and $\varGamma := \{p \in \mathbb {R}_{\geq 0}^{N} | p^{T} e = 1\}$ be the standard simplex in $\mathbb {R}^{N}$. Then obviously λ ^∗= maxv∈B minp∈Γ p ^T f(v), and by duality

$$\lambda^{*} = \max_{v\in B} \min_{p \in \varGamma} p^{T} f(v) = \min_{p \in \varGamma} \max_{v\in B} p^{T} f(v) = \min_{p \in \varGamma} \varLambda(p) $$

where Λ(p):= max{p ^T f(v)|v∈B} is the block problem associated to the max-min resource sharing problem.

Let $\bar {\varepsilon } > 0$. We are looking for an approximate solution to (48):

$$ \text{Find } v \in B \text{ such that } f(v) \geq \left( {1 - \bar{\varepsilon}}\right) \lambda^{*} e~~. $$

(49)

This can be done with an algorithm by Grigoriadis et al. [12] (see also [14]). This algorithm relies on a blocksolver A B S(p,t) that solves the block problem with accuracy $t = \frac {\bar {\varepsilon }}{6}$:

$$ \text{Find } v \in B \text{ for a given } p \in \varGamma, t = \varTheta(\bar{\varepsilon}), \text{ such that } p^{T} f(v) \geq \left( {1 - t}\right) \varLambda(p). $$

(50)

First, the algorithm computes an initial solution

$$ v^{(0)} := \frac{1}{N} {\sum}_{i=1}^{N} \hat{v}^{(i)} \text{ where } \hat{v}^{(i)} := ABS\left( {e_{i},\frac{1}{2}}\right)~~. $$

(51)

The vector $e_{i} \in \mathbb {R}^{N}$ is the unit vector with 1 in the i.th component and 0 otherwise, therefore $\hat {v}^{(i)}$ satisfies ${e_{i}^{T}} f\left (\hat {v}^{(i)}\right ) = f_{i}\left (\hat {v}^{(i)}\right ) \geq \left (1 - \frac {1}{2}\right ) \varLambda (e_{i}) = \frac {1}{2} \varLambda (e_{i})$. The algorithm then improves upon this initial solution v ⁽⁰⁾: it sets v:=v ⁽⁰⁾ and computes the solution 𝜃(f(v)) of

$$ \frac{t}{N} {\sum}_{i=1}^{N} \frac{\theta}{f_{i}(v) - \theta} = 1, \ \theta \in (0, \min\{f_{1}(v), \ldots, f_{N}(v)\})~~. $$

(52)

Note that the solution 𝜃(f(v)) is unique because the sum is strictly increasing in 𝜃. Then, a new vector p=p(f(v))=(p ₁,…,p _N )^T∈Γ is computed with

$$ p_{i} := \frac{t}{N} \frac{\theta(f(v))}{f_{i}(v) - \theta(f(v))} \text{ for } i = 1, \ldots, N~~. $$

(53)

After this, $\hat {v} := ABS(p(f(v)),t)$ is calculated as well as the following stopping condition checked:

$$ \nu(v,\hat{v}) := \frac{p^{T} f(\hat{v}) - p^{T} f(v)}{p^{T} f(\hat{v}) + p^{T} f(v)} \leq t ~~. $$

(54)

If not satisfied, v is set to $v = (1 - \tau ) v + \tau \hat {v}$, where

$$ \tau = \tau(f(v)) := \frac{t \theta(f(v)) \nu(v,\hat{v})}{2 N \left( p^{T} f(v) + p^{T} f(\hat{v})\right)}~~. $$

(55)

The algorithm then restarts with the calculation of 𝜃(f(v)) and continues until $\nu (v,\hat {v}) \leq t$. Then it returns v. A speedup is possible by beginning with $\bar {\varepsilon }_{0} = 1 - \frac {1}{2 M}$ and setting $\bar {\varepsilon }_{s} = \frac {\bar {\varepsilon }_{s-1}}{2}$ when the stopping condition is met until the stopping condition is satisfied for an $\bar {\varepsilon }_{s} \leq \bar {\varepsilon }$. The algorithm is presented in Fig. 12. (The pseudocode representation was adapted from [3]).

Fig. 12

The max-min resource sharing algorithm (representation adapted from [3])

Theorem 47

Let $\bar {\varepsilon } > 0$ and let $f_{i} : B \rightarrow \mathbb {R}_{\geq 0}$ , i=1,…,N, be non-negative concave functions over a non-empty, convex and compact set $B \subset \mathbb {R}^{L}$. Then the algorithm presented in Fig. 12 finds an approximate solution v∈B of the max-min resource sharing problem (48), where v satisfies (49). The algorithm needs $O\left (N \left (\log N + \frac {1}{\bar {\varepsilon }^{2}}\right )\right )$ iterations, where in each iteration a call to the blocksolver is needed as well as an overhead of $O\left (N \log \log \left (N \frac {1}{\bar {\varepsilon }}\right )\right )$ incurs.

Proof

Correctness and running time were proved by Grigoriadis et al. [12] (see also [14]). □

1.2 A. 2 Missing Proofs

Proof (Lemma 11)

Note that the configuration generated by the blocksolver (7) does not depend on r, but only on the simplex vector p. For different values r, but the same vector p, the blocksolver will choose the same bin size and the same configuration and then set the corresponding variable $v_{j_{0}}^{(l_{0})} := \frac {r}{c_{l_{0}}}$.

Using the notation of the algorithm in Fig. 12, we have $ABS_{r_{p}}(p,t) = r_{p} \cdot ABS_{1}(p,t)$ where $ABS_{r_{p}}$ is the blocksolver for r=r _p and A B S ₁ the blocksolver for r=1. Moreover, we have $f_{i}(v) = \tilde {a}_{i}^{T} v$, where $\tilde {a}_{i}$ is the i.th row of the matrix $\tilde {A}$ of (3).

This allows us to show the theorem by induction. (To simplify notation, we will denote all variables and constants for r=1 and for r=r _p by a corresponding index.) For s=0, we have $v^{(0)}_{r_{p}} = r_{p} \cdot v_{1}^{(0)}$ because of (51): the initial solution $v^{(0)}_r$ is a linear combination of the different A B S _r (e _m ,t), where r∈{1,r _p }.

Let us now assume that $v^{({s^{\prime }})}_{r_{p}} = r_{p} \cdot v^{({s^{\prime }})}_{1}$ for all s ^′≤s−1, in particular $v_{r_{p}} = v^{({s-1})}_{r_{p}} = r_{p} \cdot v^{({s-1})}_{1} = r_{p} \cdot v_{1}$. We have $\theta _{r_{p}}(f(v_{r_{p}})) = r_{p} \cdot \theta _{1}(f(v_{1}))$ because the solution 𝜃(f(v)) of (52) is unique, and r _p ⋅𝜃 ₁(f(v ₁)) is a solution to it because of the linearity of f _i (v). This demonstrates that $p_{r_{p}}(f(v_{r_{p}})) = p_{1}(f(v_{1}))$ according to Definition (53). Thus, we have $\hat {v}_{r_{p}} = ABS_{r_{p}}(p_{r_{p}}) = ABS_{r_{p}}(p_{1}) = r_{p} \cdot ABS_{1}(p_{1}) = r_{p} \cdot \hat {v}_{1}$ as explained above. Moreover, $\nu _{r_{p}}(v_{r_{p}},\hat {v}_{r_{p}}) = \nu _{1}(v_{1},\hat {v}_{1})$ holds according to Definition (54). Similarly, the new $v_{r_{p}} = v^{({s})}_{r_{p}} := (1- \tau _{r_{p}}) v_{r_{p}} + \tau _{r_{p}} \hat {v}_{r_{p}}$ and the new $v_{1} = v^{({s})}_{1} := (1 - \tau _{1}) v_{1} + \tau _{1} \hat {v}_{1}$ satisfy $v^{({s})}_{r_{p}} = r_{p} \cdot v^{({s})}_{1}$ because we have $\tau _{r_{p}} = \tau _{1}$ according to Definition (55). Finally, the algorithm will finish for r=1 and r=r _p after the exact same number of iterations because $\nu _{r_{p}}(v_{r_{p}},\hat {v}_{r_{p}}) = \nu _{1}(v_{1},\hat {v}_{1})$ holds. This finishes our proof. □

We finish this Section with the proof of Theorem 12.

Proof (Theorem 12)

For simplicity, we write d _k =d and M ₁=M. First, we solve (2) with r=1 as explained above to obtain a solution $\tilde {\tilde {v}}$ with

$$\begin{array}{@{}rcl@{}} \sum\limits_{l} c_{l} {\sum}_{j} \tilde{\tilde{v}}_{j}^{(l)} &=& 1 \\ {\sum}_{l} {\sum}_{j} a\left( K_{j}^{(l)},b_{i}\right) \tilde{\tilde{v}}_{j}^{(l)} &=:& \beta_{i} \geq (1 - \bar{\varepsilon}) \lambda_{1} n_{i} \quad \text{ for } i = 1, \ldots, d. \end{array} $$

(56)

Here, λ ₁ is the optimum of (2) for r=1. Note that we have set $\bar {\varepsilon } = \frac {\varepsilon }{4}$.

The max-min resource sharing algorithm needs at most $O\left (d \left (\log d + \frac {1}{\bar {\varepsilon }^{2}}\right )\right ) = O\left (d \left (\log d + \frac {1}{\varepsilon ^{2}}\right )\right )$ iterations, where a call to the blocksolver $KP\left (d, M, c_{\min }, \frac {\bar {\varepsilon }}{6}\right )$ is needed in each iteration and an overhead of $O\left (d \log \log \left (d \frac {1}{\bar {\varepsilon }}\right )\right ) = O\left (d \log \log \right . \left .\left (d \frac {1}{\varepsilon }\right )\right )$ incurs (see [12,14] and Theorem 47). In total, we get the running time $O\left (d \left (\log (d) + \frac {1}{\varepsilon ^{2}}\right ) \max \left \{KP\left (d, M, c_{\min }, \frac {\bar {\varepsilon }}{6}\right ), O\left (d \log \log \left (d \frac {1}{\varepsilon }\right ) \right ) \right \} \right )$.

Note that at most one new configuration is added in every iteration of the max-min resource sharing algorithm. Therefore, there are at most $O\left (d \left (\log d + \frac {1}{\varepsilon ^{2}}\right )\right )$ columns in $\tilde {A}$, which is also an upper bound on the number of variables $\tilde {\tilde {v}}_{j}^{(l)} > 0$ of the final solution $\tilde {\tilde {v}}$.

After having determined $\tilde {\tilde {v}}$, we reduce the number of positive variables by finding a basic solution $\tilde {v}$ of (56) with only d+1 variables $\tilde {v}_{j}^{(l)} > 0$. Beling and Megiddo [1] have found an implementation of the standard technique to do so with running time $O\left (d^{1.594} d \left (\log d + \frac {1}{\varepsilon }^{2}\right )\right ) = O\left (d^{2.594} \left (\log d + \frac {1}{\varepsilon ^2}\right ) \right )$. Since $f(\tilde {\tilde {v}}) = \tilde {A} \tilde {\tilde {v}} = \tilde {A} \tilde {v} = f(\tilde {v})$, the value $r_{0} = \frac {1 - \bar {\varepsilon }}{\min \{f_{1}(\tilde {\tilde {v}}_{1}), \ldots , f_{d}(\tilde {\tilde {v}}_{1})\}}$ remains unchanged by this. Note that ${\sum }_{l} c_{l} {\sum }_{j} \tilde {\tilde {v}}_{j}^{(l)} = {\sum }_{l} c_{l} {\sum }_{j} \tilde {v}_{j}^{(l)} = 1$ still holds, too.

After this reduction, we multiply the d+1 positive variables $\tilde {v}_{j}^{(l)}$ by $r_{0} \cdot (1 + 4 \bar {\varepsilon })$ to obtain the solution of (2). This can obviously be done in time O(d + 1). We get the solution v within the running time stated in Theorem 12. □

Appendix B: KPIP: Adding the Small Items Efficiently

The ideas in the following section are taken from Lawler’s paper [21].

First, let J:={a ₁,…,a _m } be a set of knapsack items. Let σ:{1,…,m}→{1,…,m} be the permutation that sorts the items according to their efficiency $\frac {p(a)}{s(a)}$ in non-increasing order, i.e. $\frac {p(a_{\sigma (1)})}{s(a_{\sigma (1)})} \geq {\ldots } \geq \frac {p(a_{\sigma (j)})}{s(a_{\sigma (j)})} \geq {\ldots } \geq \frac {p(a_{\sigma (m)})}{s(a_{\sigma (m)})}$. (In case of ties, the item with smaller index can be defined to have the smaller efficiency.) Moreover, let $\tilde {C}$ be a knapsack size. We now want to add the items greedily to knapsack $\tilde {C}$ until the knapsack is full without sorting the items according to their efficiency.

To do so, let J ⁽¹⁾ the solution set, i.e. the m ^′ items such that $J^{({1})} = \left \{a_{\sigma ({1})}, \ldots , a_{\sigma ({m^{\prime }})}\right \}$ and $s\left (J^{({1})}\right ) = {\sum }_{j=1}^{m^{\prime }} s(a_{\sigma ({j})}) \leq \tilde {c} < s\left (J^{({1})}\right ) + s\left (a_{\sigma ({m^{\prime }+1})}\right ) = {\sum }_{j = 1}^{m^{\prime }+1} s\left (a_{\sigma ({j})}\right )$. We will now iteratively construct pairwise disjoint item sets $\tilde {J}_{1}, \ldots , \tilde {J}_{k}$ and $\bar {J}_{k}$ such that

$$ \bigcup_{j = 1}^{k} \tilde{J}_{j} \subseteq J^{({1})} \subseteq \bigcup_{j = 1}^{k} \tilde{J}_{j} \cup \bar{J}_{k} $$

(57)

until having found one $\bar {k}$ such that $\bigcup _{j = 1}^{\bar {k}} \tilde {J}_{j} = J^{(1)}$ or $J^{(1)} = \bigcup _{j = 1}^{\bar {k}} \tilde {J}_{j} \cup \bar {J}_{\bar {k}}$.

We introduce the notion of the median set $\tilde {J}$ of an item set $\bar {J} \subseteq J$: if $|{\bar {J}}| = r$, then the median set $\tilde {J}$ consists of the first $\lfloor {\frac {r}{2}}\rfloor + 1$ most efficient items of $\bar {J}$. Thus, the median set consists of the items sorted according to their efficiency up to and including the median. For instance, we have for $\bar {J} = J$ that $\tilde {J} = \{a_{\sigma (1)}, a_{\sigma (2)}, \ldots , a_{\sigma (\lfloor {\frac {m}{2}}\rfloor +1)}\}$. Since the median of a set can be found in time and space $\mathcal {O}\left ({|{\bar {J}}|}\right )$, this is also the running time and space requirement for determining $\tilde {J}$. Note that $\frac {p \left (a_{\sigma (\lfloor {\frac {r}{2}}\rfloor +1)}\right )}{s\left (a_{\sigma (\lfloor {\frac {r}{2}}\rfloor +1)}\right )} = \frac {p\left (a_{\sigma (\lfloor {\frac {r}{2}}\rfloor + 2)}\right )}{s\left (a_{\sigma (\lfloor {\frac {r}{2}}\rfloor +2)}\right )}$ may hold, i.e. the median set is not always equal to $\left \{a \in \tilde {J} \ | \ \frac {p(a)}{s(a)} \geq \frac {p\left (a_{\sigma (\lfloor {\frac {r}{2}}\rfloor + 1)}\right )}{s\left (a_{\sigma (\lfloor {\frac {r}{2}}\rfloor + 1)}\right )}\right \}$.

Let us determine J ⁽¹⁾. Set $\tilde {J}_{1} := \emptyset$ and $\bar {J}_{1} := J$. Obviously, $\tilde {J}_{1} \subseteq J^{(1)} \subseteq \tilde {J}_{1} \cup \bar {J}_{1}$, i.e. Property (57) holds, and the item sets are pairwise disjoint. Now, let $\bigcup _{j = 1}^{k} \tilde {J}_{j}$ and $\bar {J}_{k}$ be the current sets. Let $\tilde {J}$ be the median set of $\bar {J}_{k}$. If the items in $\bigcup _{j = 1}^{k} \tilde {J}_{j} \cup \tilde {J}$ fit into $\tilde {C}$, then the optimal set J ⁽¹⁾ has to contain $\bigcup _{j = 1}^{k} \tilde {J}_{j} \cup \tilde {J}$ as a subset. We set $\tilde {J}_{k+1} := \tilde {J}$ and $\bar {J}_{k+1} := \bar {J}_{k} {\backslash } \tilde {J}$ and replace k by k+1. Then Property (57) still holds, and the item sets are still pairwise disjoint.

On the other hand, if the items in $\bigcup _{j = 1}^{k} \tilde {J}_{j} \cup \tilde {J}$ do not fit into $\tilde {C}$, then $\bigcup _{j = 1}^{k} \tilde {J}_{j} \cup \tilde {J}$ contains too many items, i.e. $J^{(1)} \subsetneq \bigcup _{j = 1}^{k} \tilde {J}_{j} \cup \tilde {J}$. Thus, we set $\bar {J}_{k} := \tilde {J}$. Property (57) holds, and the item sets are still pairwise disjoint.

The procedure continues until $\bigcup _{j = 1}^{k} \tilde {J}_{j} = J^{(1)}$ or $\bigcup _{j = 1}^{k} \tilde {J}_{j} \cup \bar {J}_{k} = J^{(1)}$. As the size of the set $\bar {J}_{k}$ halves in every iteration, we get an overall running time of $\mathcal {O}\left ({m + \frac {m}{2} + \frac {m}{4} + \cdots }\right ) = \mathcal {O}\left ({m}\right )$. Moreover, we only have to store the current union set $\bigcup _{j = 1}^{k} \tilde {J}_{j}$ as well as the current sets $\bar {J}_{k}$ and $\tilde {J}$ together with their corresponding total sizes $s(\bigcup _{j = 1}^{k} \tilde {J}_{j}), s(\bar {J}_{k})$ and $s(\bar {J}_{k})$. Thus, we only need space in $\mathcal {O}\left ({m}\right )$.

Lemma 48

Let J:={a ₁ ,…,a _m } be a set of knapsack items together with a knapsack size $\tilde {C}$. We can find the greedy solution J ⁽¹⁾ for this knapsack size by a median-based divide-and-conquer strategy in time and space $\mathcal {O}\left ({|{J}|}\right ) =\mathcal {O}\left ({m}\right )$.

Consider now a 0-1 knapsack instance with n items and the knapsack size c, which is solved with Lawler’s FPTAS, i.e. the algorithms presented in Sections 3.4.3 and 3.4.4 for only one knapsack size C = {c}. We assume that the $F_{n_{b}}(i)$ are not dominated (otherwise we discard dominated ones as seen in Lemma 29), i.e. $F_{n_{b}}(1) < {\ldots } < F_{n_{b}}(i_{c})$. Here, i _c is the largest profit we have to consider, where we have without loss of generality $F_{n_{b}}(i_{c}) \leq c$.

Take two profits i<i ^′′. Assume that the set of the small items J ⁽ⁱ⁾ and $J^{({i^{\prime \prime }})}$ that are added to the remaining knapsack space $c - F_{n_{b}}(i)$ and $c - F_{n_{b}}(i^{\prime \prime })$ in Step (5.4.1) (see also Definition (31)) are known. Then obviously $J^{({i})} \supseteq J^{({i^{\prime \prime }})}$ holds because $c - F_{n_{b}}(i) > c - F_{n_{b}}(i^{\prime \prime })$. Furthermore, we have by definition $\phi (c - F_{n_{b}}(i)) = p(J^{({i})})$ and $\phi (c - F_{n_{b}}(i^{\prime \prime })) = p(J^{({i^{\prime \prime }})})$. Let us take now a profit i ^′ with i<i ^′<i ^′′ and therefore with property $F_{n_{b}}(i) < F_{n_{b}}(i^{\prime }) < F_{n_{b}}(i^{\prime \prime })$. We know that $J^{({i^{\prime \prime }})} \subseteq J^{({i^{\prime }})} \subseteq J^{({i})}$, i.e. we have $J^{({i^{\prime }})} = J^{({i^{\prime \prime }})} \cup \tilde {J}^{({i^{\prime }})}$ for the appropriate item set $\tilde {J}^{({i^{\prime }})} \subseteq \tilde {J}^{({i})} := J^{({i})} {\backslash } J^{({i^{\prime \prime }})}$. Thus, $\tilde {J}^{({i^{\prime }})}$ are the items that can greedily be added to $c - F_{n_{b}}(i^{\prime })$ when the items $J^{({i^{\prime \prime }})}$ are already in the knapsack.

Therefore, it is sufficient to find the item set $\tilde {J}^{({i^{\prime }})}$, and we can do so by applying Lemma 48 to item set $\tilde {J}^{({i})}$ and knapsack size $\tilde {c} = c - F_{n_{b}}(i^{\prime }) - s\left (J^{({i^{\prime \prime }})}\right )$.

Lemma 49

We can determine the set $\tilde {J}^{({i^{\prime }})}$ and therefore $J^{({i^{\prime }})} = J^{({i^{\prime \prime }})} \cup \tilde {J}^{({i^{\prime }})}$ in time and space $\mathcal {O}\left ({|{\tilde {J}^{({i})}}|}\right ) = \mathcal {O}\left ({|{J^{({i})} {\backslash } J^{({i^{\prime \prime }})}}|}\right )$. We only have to know the item set $\tilde {J}^{({i})} = J^{({i})} {\backslash } J^{({i^{\prime \prime }})}$ and the size $s(J^{({i^{\prime \prime }})})$ to find $\tilde {J}^{({i^{\prime }})}$ itself.

We can now determine all $\phi (c - F_{n_{b}}(i))$ again by a divide-and-conquer strategy. Let J be the set of all small items for c, let i _c be the largest profit i we have to consider, and let s be the number of the current iteration of the divide-and-conquer algorithm. We start with s=0. We take the profit $\tilde {i} := \lfloor {\frac {i_{c}}{2}}\rfloor + 1$, i.e. the median of 1,…,i _c , and apply Lemma 48 to it with $\tilde {c} = c - F_{n_{b}}(\tilde {i})$. We find $J^{({\tilde {i}})} = \tilde {J}^{(\tilde {i})}$ in time and space $\mathcal {O}\left ({|{J}|}\right ) \subseteq \mathcal {O}\left ({n}\right )$. We save $\tilde {J}^{(\tilde {i})}$ and $s(J^{(\tilde {i})})$. The missing sets J ⁽ⁱ⁾ will now be constructed inductively.

Let s be the current iteration and $r = r_{s} \in \mathbb {N}$ be a value such that i ₁<i ₃<…<i _2r−1<i _2r+1 are the profits for which the item sets $\tilde {J}^{({i})}$ have been determined and saved so far. Moreover, we have also stored the corresponding sizes s(J ⁽ⁱ⁾). Note that $\tilde {J}^{({i_{2r+1}})} = J^{({i_{2r+1}})}$ and that $J^{({i})} = \tilde {J}^{({i})} \cup {\ldots } \cup \tilde {J}^{({i_{2r+1}})}$. We take the median $i_{2r^{\prime }}$ of every pair $i_{2r^{\prime }-1}$ and $i_{2r^{\prime }+1}$ as well as the median i ₀ of 1 and i ₁ and the median i _2r+2 of i _2r+1 and i _c . This can be done in time and space $\mathcal {O}\left ({r}\right )$. Thus, we have

$$1 \leq i_{0} < i_{1} < i_{2} < {\ldots} < i_{2r-1} < i_{2r} < i_{2r+1} < i_{2r+2} \leq i_{c}~~. $$

Note that $i_{2r^{\prime }-1}$ and $i_{2r^{\prime }+1}$ may be neighbours – then $i_{2r^{\prime }}$ does not exist – or that i ₀=1. If i _2r+1=i _c −1, we also set i _2r+2=i _c .

For every new $i_{2r^{\prime }}$, we have $F_{n_{b}}(i_{2r^{\prime }-1}) < F_{n_{b}}(i_{2r^{\prime }}) < F_{n_{b}}(i_{2r^{\prime }+1})$. We can determine $\tilde {J}^{({i_{2r^{\prime }}})}$ as the subset of $\tilde {J}^{({i_{2r^{\prime }-1}})}$ with Lemma 49 in time and space $\mathcal {O}\left ({|{\tilde {J}^{({i_{2r^{\prime }-1}})}}|}\right ) = \mathcal {O}\left ({|{J^{({i_{2r^{\prime }-1}})} {\backslash } J^{({i_{2r^{\prime }+1}})}}|}\right )$.

We then save the total size $\phantom {\dot {i}\!}s\left (J^{({i_{2r^{\prime }}})}\right ) = s\left (\tilde {J}^{({i_{2r^{\prime }}})}\right ) + s\left (J^{({i_{2r^{\prime }+1}})}\right )$. Moreover, we replace $\tilde {J}^{({i_{2r^{\prime }-1}})}$ by $\tilde {J}^{({i_{2r^{\prime }-1}})} {\backslash } \tilde {J}^{({i_{2r^{\prime }}})}$ so that we now have $\phantom {\dot {i}\!}J^{({i_{2r^{\prime }-1}})} = \tilde {J}^{({i_{2r^{\prime }-1}})} \cup J^{({i_{2r^{\prime }}})}$. These operations additionally need time and space in $\phantom {\dot {i}\!}\mathcal {O}\left ({|{J^{({i_{2r^{\prime }-1}})} {\backslash } J^{({i_{2r^{\prime }+1}})}}|}\right )$.

A special case is i ₀, where we have $\phantom {\dot {i}\!}J^{({i_{1}})} \subseteq J^{({i_{0}})} \subseteq J$ so that we use the set $\phantom {\dot {i}\!}J {\backslash } J^{({i_{1}})}$ for the algorithm of Lemma 49, and all operations above need time and space in $\phantom {\dot {i}\!}\mathcal {O}\left (|{J {\backslash } J^{({i_{1}})}|}\right )$.

It is of course possible that e.g. already $\phantom {\dot {i}\!}J^{({i_{2r^{\prime }-1}})} = J^{({i_{2r^{\prime }+1}})}$ holds so that we get $\phantom {\dot {i}\!}\tilde {J}^{({i_{2r^{\prime }}})} = \emptyset$ and a “running time” of $\mathcal {O}\left ({|{J^{({i_{2r^{\prime }-1}})}}|}\right ) = 0$. To take into account the running time and space of such cases – we still have e.g. to save $\phantom {\dot {i}\!}\tilde {J}^{({i_{2r^{\prime }}})} = \emptyset$ – we additionally add $\mathcal {O}\left ({1}\right )$ to the time and space needed for each $i_{2r^{\prime }}$, which yields an additional cost of $\mathcal {O}\left ({r}\right )$ in time and space for iteration s.

To sum up, we need time and space in $\mathcal {O}\left ({|{J}| + r}\right ) = \mathcal {O}\left ({n + r_{s}}\right )$ for iteration s because the $\phantom {\dot {i}\!}J^{({i_{2r^{\prime }-1}})} {\backslash } J^{({i_{2r^{\prime }+1}})}$ and $\phantom {\dot {i}\!}J {\backslash } J^{({i_{1}})}$ are disjoint sets. Obviously, r _s and the number of profits i we have considered so far double in each iteration so that we only need $\mathcal {O}\left ({\log {i_{c}}}\right )$ iterations in total to find the values for all $F_{n_{b}}(i)$.

For the overall time and space bound, let us assume that we have c=c _l for one c _l ∈C _b of our 0-1 KPIP algorithm. Thus, we get with $i_{c_{l}} \leq i_{\max } \in \mathcal {O}\left ({\frac {1}{\varepsilon ^{2}} \frac {c_{b,\max }}{c_{b,\min }}}\right )$ (see (42)) and $r_{s} \in \mathcal {O}\left ({2^{s}}\right )$ a total running time of

$$\begin{array}{@{}rcl@{}} \mathcal{O}\left( { {\sum}_{s=0}^{\mathcal{O}\left( {\log\left( {i_{\max}}\right) }\right) } n + r_{s} }\right) & =& \mathcal{O}\left( { n \cdot \log\left( { \frac{1}{\varepsilon^{2}} \frac{c_{b,\max}}{c_{b,\min}}}\right) + \sum\limits_{s=0}^{\mathcal{O}\left( {\log\left( { i_{\max}}\right) }\right) } 2^{s} }\right) \\ & =& \mathcal{O}\left( {n \cdot \log\left( { \frac{1}{\varepsilon^{2}} \frac{c_{b,\max}}{c_{b,\min}}}\right) + \frac{1}{\varepsilon^{2}} \frac{c_{b,\max}}{c_{b,\min}}}\right)~~. \end{array} $$

For the overall space requirement, note that we only have to save the $\tilde {J}^{({i})}$ and s(J ⁽ⁱ⁾) after one iteration s, which need $\mathcal {O}\left ({r_{s} + n}\right ) \subseteq \mathcal {O}\left ({i_{\max } + n}\right )$ in total. Together with the space needed for the operations during one iteration s, we require space in

$$\mathcal{O}\left( {i_{c_{l}} + n + r_{s}}\right) \subseteq \mathcal{O}\left( {\frac{1}{\varepsilon^{2}} \frac{c_{b,\max}}{c_{b,\min}} + n}\right)~~. $$

The actual values $\phantom {\dot {i}\!}\phi _{l}(c_{l} - F_{n_{b}}(i))$ can easily be determined in time and space $\mathcal {O}\left ({i_{\max }+n}\right )$ thanks to the J ⁽ⁱ⁾, which is dominated by the expressions above.

We have proved Theorem 37. It is possible to heuristically improve the running time: let J ^′ be the first m ^′ most efficient small items so that ${\sum }_{r^{\prime }=1}^{m^{\prime }} s(a_{\sigma (r^{\prime })}) \leq c_{l}$, but ${\sum }_{r^{\prime }=1}^{m^{\prime }+1} s(a_{\sigma (r^{\prime })}) > c_{l}$. By a binary search as above, J ^′ can be found in $\mathcal {O}\left ({m}\right ) \subseteq \mathcal {O}\left ({n}\right )$ and then J ^′ instead of J used to determine all ϕ _l (c _l −F _n (i)) and $\tilde {J}^{({i})}$.

Appendix C: The Bounded KPIP: The Details

Proof (Theorem 46)

Here, we normally save how many copies of one item type we use. For instance, every set does not save the individual item copies in it, but instead how many times each item type is used. We have for example $\tilde {J}^{({i})} = \{(a_{\sigma (j)} , g_j)), \ldots , (a_{\sigma ({j^{\prime }})},g_{j^{\prime }})\}$, where $g_{j^{\prime \prime }}$ denotes the number of copies of item $a_{\sigma ({j^{\prime \prime }})}$ in the set $\tilde {J}^{({i})}$. Note that the usual algorithm to find the median of a set can be adapted to be still linear in the number of different item types in a set.

The median-based search, which is used to get the $\phantom {\dot {i}\!}\bar {P}_{c_{l}}$ and P ₀ in Step (3) and the small-item values $\phantom {\dot {i}\!}\phi _{l}(c_{l} - F_{n_{b}}(i))$ in Step (5.4.1), does not change much.

Let $F_{n_{b}}(i)$ and $F_{n_{b}}(i^{\prime \prime })$ be two values as seen in Appendix B with their sets $\tilde {J}^{({i})}, J^{({i})}$ and $\tilde {J}^{({i^{\prime \prime }})}, J^{({i^{\prime \prime }})}$, respectively. Determining $\tilde {J}^{({i^{\prime }})}$ for i<i ^′<i ^′′ can now be done linear in the number of item types in $\tilde {J}^{({i})}$ so that the algorithm works as before. We may however have e.g. $\tilde {J}^{({i})} = \{(a_{\sigma ({j})},g_{j}), \ldots , (a_{\sigma ({j^{\prime }})},g_{j^{\prime }})\}$ and $J^{({i^{\prime \prime }})} = \{(a_{\sigma ({j^{\prime }})},\tilde {g}_{j^{\prime }}), \ldots , (a_{\sigma ({j^{\prime \prime }})},\tilde {g}_{j^{\prime \prime }})\}$, i.e. both contain item type $a_{\sigma ({j^{\prime }})}$, each with its corresponding multiple. In iteration s of the algorithm of Theorem 37, the sets $\tilde {J}^{({i_{0}})}, \tilde {J}^{({i_{1}})}, \ldots , \tilde {J}^{({i_{2r_{s} + 2}})}$ therefore may no longer be “disjoint” by sharing copies of the same item type. However, we have by definition of the sets $\tilde {J}^{(\tilde {i})}$ that $\tilde {J}^{({i_{2r_{s} + 2}})}$ contains the most efficient items and that the efficiencies do not increase from one item set to another: the items are added according to the order σ from the most to the least efficient items. Thus, the number of overlapping item types is bounded by $\mathcal {O}\left ({|{J}| + r_{s}}\right )$, which does not change the asymptotic running time and space requirement of the algorithm. The same properties also hold for the operations in Step (3) so that the overall running time and space requirement of this step do not change either.

For the large-item computation in Step (5.3), we instead take item copies. Fix one C _b . Let $\tilde {a}_{1,j}, \ldots , \tilde {a}_{t,j}$ be the large item types that have the scaled profit q _j , sorted according to their size in non-decreasing order (i.e. $s(\tilde {a}_{1,j}) \leq {\ldots } \leq s(\tilde {a}_{t,j})$), and let $\tilde {d}_{1,j}, \ldots , \tilde {d}_{t,j}$ be their corresponding maximal possible multiple. Since a solution can contain at most n _L,j large items for every q _j (see (46)), it is sufficient for the large-item computation to take copies of the items of smallest size until having n _L,j of them. Hence, it is sufficient to find t ^′≤t such that

$$\tilde{d}_{1,j} + {\cdots} + \tilde{d}_{t^{\prime}-1,j} + \underbrace{(\tilde{d}_{t^{\prime},j} - h_{j})}_{:= \tilde{\tilde{d}}_{t^{\prime},j}} = n_{L,j}, \quad 0 \leq h_{j} \leq \tilde{d}_{t^{\prime},j} - 1~~, $$

and then take $\tilde {d}_{t^{\prime \prime },j}$ copies of $\tilde {a}_{t^{\prime \prime },j}$, t ^′′∈{1,…,t ^′−1}, and $\tilde {\tilde {d}}_{t^{\prime },j}$ copies of $\tilde {a}_{t^{\prime },j}$. This method already yields the bound $n_{b} \leq n_{L} \in \mathcal {O}\left ({\frac {1}{\varepsilon ^{2}}\frac {c_{b,\max }}{c_{b,\min }}}\right )$ for the large items as seen in Lemma 39.

To improve the running time, Lawler’s idea for the unbounded case can be slightly modified as proposed by Plotkin et al. [24, p. 296]: item copies $\tilde {a}^{(r)}_{t^{\prime \prime },j}$ are created with

$$\begin{array}{@{}rcl@{}} &&\tilde{a}_{t^{\prime\prime},j}^{(r)} \text{ with } p\left( \tilde{a}_{t^{\prime\prime},j}^{(r)}\right) = 2^{r} p(\tilde{a}_{t^{\prime\prime},j}), s\left( \tilde{a}_{t^{\prime\prime},j}^{(r)}\right) = 2^{r} s\left( \tilde{a}_{t^{\prime\prime},j}\right) \\&&\text{ for } r \in \left\{0, \ldots, \left\lfloor{\log_{2}\left( \tilde{d}_{t^{\prime\prime},j}\right)}\right\rfloor-1\right\}\\ \text{and } \quad &&\tilde{a}_{t^{\prime\prime},j}^{(r)} \text{ with } p\left( \tilde{a}_{t^{\prime\prime},j}^{(r)}\right) = \left( \tilde{d}_{t^{\prime\prime},j} - 2^{\left\lfloor{\log_{2}\left( \tilde{d}_{t^{\prime\prime},j}\right)}\right\rfloor} + 1\right) p\left( \tilde{a}_{t^{\prime\prime},j}\right),\\ &&s\left( \tilde{a}_{t^{\prime\prime},j}^{(r)}\right) = \left( \tilde{d}_{t^{\prime\prime},j} - 2^{\left\lfloor{\log_{2}(\tilde{d}_{t^{\prime\prime},j})}\right\rfloor } + 1\right) s\left( \tilde{a}_{t^{\prime\prime},j}\right) \\ &&\text{ for } r = \lfloor{\log_{2}(\tilde{d}_{t^{\prime\prime},j})}\rfloor~~. \end{array} $$

The only exception are the item copies $\tilde {a}_{t^{\prime },j}^{(r)}$ of $\tilde {a}_{t^{\prime },j}$ where $\tilde {d}_{t^{\prime \prime },j}$ is replaced by $\tilde {\tilde {d}}_{t^{\prime },j} = \tilde {d}_{t^{\prime },j} - h_{j}$. These multiple copies are enough to represent all choices of item copies. Similar to the unbounded case, only n _L,j item copies of smallest size for one profit q _j have to be kept after having created the copies. It is however not possible to keep only the item $\tilde {a}^{(r)}_{t^{\prime \prime },j}$ of smallest size because Lemma 44 is not valid for BKPIP.

All these operations can also be done in time linear in the number of item types because the median finding algorithm still runs in linear time.

For the entire BKPIP algorithm, the running time and space bound can be determined like for the improved 0-1 KPIP algorithm in Lemma 41. The additional time to take the item copies in Step (5.2) is dominated by the large-item computation in Step (5.3). □