Wholesale price discrimination with interdependent retailers

Abstract

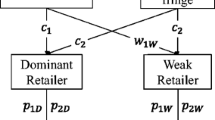
This paper examines the relationship between one manufacturer and two retailers who sell a product on their downstream markets. If a retailer invests in activities that enhance demand and, for example, improve the perceived image of the product, he or she might attract more customers, as well as increase the sales volumes of other retailers. In such a situation, free rider problems arise between the retailers, which finally lead to reduced sales efforts. We show that for linear wholesale prices, the manufacturer’s pricing strategy depends on the retailers’ investment costs and derive conditions for the optimality of wholesale price discrimination. We find that for low and high costs the manufacturer charges the retailers identical wholesale prices and thus does not have to bear any agency costs due to free riding. In all other cases, the manufacturer mitigates this problem by engaging in wholesale price discrimination. Our results indicate why it might make sense for a manufacturer to charge different wholesale prices even when the retailers have equal cost structures, market conditions, and investment options.

Appendix

Proof of Lemma 1

First, we identify the optimal sales prices for all possible effort choices.

Suppose, that $e_1=e_2=e$. Then, differentiating (4) with respect to $p_i , i=1,2,$ and equating to zero yields¹² $\frac{\partial E{\Pi }_M}{\partial p_i}=1+e-2kp_i=0\Rightarrow p_i=\frac{1+e}{2k}$ and the manufacturer earns an expected profit of $E{\Pi }_M =\frac{({1+e})^2}{2k}-2c$.

Next, we suppose that $e_1=e_2=0$. Then differentiating (4) with respect to $p_i,i=1,2,$ and equating to zero yields $\frac{\partial E{\Pi }_M}{\partial p_i}=1-2kp_i =0\Rightarrow p_i=\frac{1}{2k}$ and the manufacturer earns an expected profit of $E{\Pi }_M=\frac{1}{2k}$.

Finally, we suppose that $e_i=e$ and $e_j=0, i,j=1,2, i\ne j$. Then, differentiating (4) with respect to $p_i$ and $p_j$ and equating to zero yields: $\frac{\partial E{\Pi }_M}{\partial p_i}=1+se-2kp_i=0\Rightarrow p_i=\frac{1+se}{2k};\frac{\partial E{\Pi }_M}{\partial p_j}=1+({1-s})e-2kp_j=0\Rightarrow p_j =\frac{1+( {1-s})e}{2k}$. Here, the manufacturer earns an expected profit of $E{\Pi }_M =\frac{( {1+se})^2+[{1+( {1-s})e}]^2}{4k}-c$.

To identify the optimal effort choice, we need to compare the expected profits of all three cases:

$$\begin{aligned}&\frac{({1+e})^2}{2k}-2c\ge \frac{1}{2k}\Leftrightarrow c\le \frac{e}{4k}({e+2}),\\&\frac{( {1+e})^2}{2k}-2c\ge \frac{( {1+se})^2+[{1+( {1-s})e} ]^2}{4k}-c\Leftrightarrow c\le \frac{e}{4k}[{e+2+2( {1-s})se}],\\&\frac{1}{2k}\ge \frac{({1+se})^2+[{1+( {1-s})e}]^2}{4k}-c\Leftrightarrow c\ge \frac{e}{4k}[{e+2-2( {1-s})se}]. \end{aligned}$$

Taking into account that $\frac{e}{4k}[{e+2-2( {1-s})se}] \le \frac{e}{4k}( {e\!+\!2})\le \frac{e}{4k}[{e\!+\!2\!+\!2({1\!-\!s})se}]$, Lemma 1 summarizes these findings.

Proof of Lemma 2

Suppose that retailer $i$ exerts effort, $e_i=e$. Then, differentiating (7) with respect to $p_i$ and equating to zero yields: $\frac{\partial E{\Pi }_{Ri}}{\partial p_i}=1-2kp_i +kw_i +e=0\Rightarrow p_i =\frac{1+e}{2k}+\frac{w_i}{2}$. The retailer earns an expected profit of $E{\Pi }_{Ri}=\frac{1}{4k}({1+e-kw_i})^2-c$.

Suppose that retailer $i$ exerts no effort, $e_i=0$. Then, differentiating (7) with respect to $p_i$ and equating to zero yields: $\frac{\partial E{\Pi }_{Ri}}{\partial p_i}=1-2kp_i +kw_i =0\Rightarrow p_i =\frac{1+kw_i }{2k}$. Here, the retailer earns an expected profit of $E{\Pi }_{Ri} =\frac{1}{4k}( {1-kw_i })^2$.

We identify the retailer’s optimal effort choice by comparing his or her profits for either decision:

$$\begin{aligned} \frac{1}{4k}( {1+e-kw_i })^2-c\ge \frac{1}{4k}[{1-kw_i} ]^2\Leftrightarrow w_i \le \frac{e+2}{2k}-\frac{2c}{e}. \end{aligned}$$

Lemma 2 summarizes these results.

Proof of Lemma 3

The manufacturer maximizes (8) subject to the constraints (9) and (10). The optimal wholesale prices $w_1$ and $w_2$ can be determined separately since they are not linked in the profit function (10) or in the constraints. Since both retailers are identical, the optimal solution always yields $w_1=w_2$. For the rest of this proof, we only refer to $w_i$ and $q_i$ with $i=1,2$.

Suppose that both retailers exert effort and $q_i=\frac{1+e-kw_i}{2}$. Then, differentiating (10) with respect to $w_i$ and equating to zero yields: $\frac{\partial E{\Pi }_M}{\partial w_i}=\frac{1+e-2kw_i}{2}=0\, \Rightarrow \, w_i =\frac{e+1}{2k}$. This is a feasible solution according to constraint (9) for $\frac{e+1}{2k}\le \frac{e+2}{2k}-\frac{2c}{e}\Leftrightarrow c\le \frac{e}{4k}$. The manufacturer’s profit is $E{\Pi }_M =\frac{( {1+e})^2}{4k}$.

Next, we suppose that no retailer exerts effort and $q_i=\frac{1-kw_i }{2}$. Then, differentiating (10) with respect to $w_i$ and equating to zero yields: $\frac{\partial E{\Pi }_M}{\partial w_i }=\frac{1-2kw_i }{2}=0\,\Rightarrow \, w_i=\frac{1}{2k}$. This is a feasible solution according to constraint (10) for $\frac{1}{2k}>\frac{e+2}{2k}-\frac{2c}{e}\Leftrightarrow c>\frac{e( {e+1})}{4k}$. The manufacturer’s profit is $E{\Pi }_M=\frac{1}{4k}$.

Since for the optimal wholesale prices $w_1=w_2$ always holds and the retailers are identical, we do not have to consider any situations in which only one retailer exerts effort.

The two solutions presented above have to be compared to the corner solution where the manufacturer sets a wholesale price at the threshold value $w_i=\frac{e+2}{2k}-\frac{2c}{e}$ in order to induce effort. This is always a feasible solution and results in a profit of $E{\Pi }_M=\frac{e^4+2e^3+8cek-16c^2k^2}{4e^2k}$.

Since $\frac{e^4+2e^3+8cek-16c^2k^2}{4e^2k}<\frac{( {1+e})^2}{4k}$ always holds, it is clear that the optimal wholesale price is $w_i=\frac{e+1}{2k}$ for $c\le \frac{e}{4k}$ and $w_i=\frac{e+2}{2k}-\frac{2c}{e}$ for $\frac{e}{4k}<c\le \frac{e( {e+1})}{4k}$. For $c>\frac{e( {e+1})}{4k}$ we have to compare the manufacturer’s profits for $w_i =\frac{e+2}{2k}-\frac{2c}{e}$ and $w_i =\frac{1}{2k}$: $E{\Pi }_M ( {w_i =\frac{e+2}{2k}-\frac{2c}{e}})\ge E{\Pi }_M (w_i ={\frac{1}{2k}})\Leftrightarrow \frac{e}{4k}[{1-\sqrt{e({e+2})}}]\le c\le \frac{e}{4k}[{1+\sqrt{e( {e+2})}}]$.

Lemma 3 summarizes these findings considering that $\frac{e}{4k}[{1-\sqrt{e({e+2})}}]<\frac{e({e+1})}{4k}<\frac{e}{4k}[ {1+\sqrt{e({e+2})}}]$.

Proof of Lemma 4

The first part of Lemma 4 follows directly from the analysis of Sect. 4.1.

Substituting the optimal retail prices (14)–(17) into the demand function (1) yields the expected order sizes:

$$\begin{aligned}&q_i \left( {e_i =\!e_j =e,p_i =\frac{1\!+e\!+kw_i }{2k}}\right) =1-k\frac{1+e+kw_i}{2k}+e=\frac{1}{2}({1+e-kw_i}),\\&q_i \left( {e_i\!=\!e,e_j = 0,p_i\!=\!\frac{1\!+\!se\!+\!kw_i}{2k}}\right) \!=\!1\!-\!k\frac{1\!+\!se\!+\!kw_i}{2k}\!+\!se\!=\!\frac{1}{2}({1\!+\!se\!-\!kw_i}),\\&\begin{aligned} q_i \left( {e_i\!=\!0,e_j\!=\!e,p_i =\frac{1\!+\!({1\!-\!s})e\!+\!kw_i}{2k}}\right) \!&=\!1\!-\!k\frac{1\!+\!({1\!-\!s})e\!+\!kw_i}{2k}\!+\!({1\!-\!s})e\\&=\frac{1}{2} \left[ {1+({1-s})e-kw_i}\right] ,\\ \end{aligned}\\&q_i \left( {e_i=e_j=0,p_i=\frac{1+kw_i}{2k}}\right) = 1-k\frac{1+kw_i }{2k}=\frac{1}{2}({1-kw_i }). \end{aligned}$$

Proof of Proposition 1

We identify the optimal wholesale prices to the maximization problem (28)–(31) in three steps. First, we derive the optimal prices in the four different cases presented in Lemma 4 without considering the constraints (29)–(31). Second, we check if and under what conditions these solutions are feasible. Third, we compare the identified and feasible interior solutions with corner solutions to finally derive those wholesale prices that maximize the manufacturer’s expected profit.

Suppose that $e_1=e_2=e$. The manufacturer then maximizes $E{\Pi }_M=\sum _{i=1}^2 w_i q_i=\sum _{i=1}^2 w_i[{\frac{1}{2}({1+e-kw_i})}]$. Differentiating with respect to $w_i$ and equating to zero yields $w_1=w_2=\frac{1+e}{2k}$. This solution is feasible according to constraint (29) if $\frac{1+e}{2k}\le {\bar{w}}\Leftrightarrow c\le \frac{se}{4k}[{1-({1-s})e}]$. The expected profit that the manufacturer can earn in this situation will be denoted by $E{\Pi }_M^1$, and $E{\Pi }_M^1=\frac{({1+e})^2}{4k}$.

In our second case, no retailer exerts effort, so $e_1=e_2=0$. The manufacturer’s goal function simplifies to $E{\Pi }_M=\sum _{i=1}^2 w_i q_i=\sum _{i=1}^2 w_i[{\frac{1}{2}({1-kw_i})}]$. This expression is maximized by setting $w_1=w_2=\frac{1}{2k}$, which is a feasible solution according to constraint (31) for $\frac{1}{2k}>{\bar{w}}\Leftrightarrow c>\frac{se}{4k}({1+se})$. We denote the achievable expected profit for the manufacturer by $E{\Pi }_M^2$, and $E{\Pi }_M^2=\frac{1}{4k}$.

The third and fourth cases in Lemma 4 describe a situation where only one of the two retailers invests in sales activities. Since they are assumed to be identical it is sufficient to analyze the case where $e_1=e$ and $e_2=0$. The manufacturer maximizes his or her expected profit $E{\Pi }_M=\sum _{i=1}^2 w_i q_i=w_1[ {\frac{1}{2}( {1+se-kw_1 })}]+w_2\{{\frac{1}{2}[{1+({1-s})e-kw_2}]}\}$ which yields $w_1=\frac{1+se}{2k}$ and $w_2 =\frac{1+( {1-s})e}{2k}$ and thus $w_1>w_2$. These wholesale prices conflict with constraint (30). Consequently, they can never yield a feasible solution, since this would require $w_1\le {\bar{w}}<\overline{\overline{w}} <w_2$. It follows that there is no interior solution to the manufacturer’s optimization problem, where only one of the two retailers exerts effort.

Since the effort level is a binary decision variable for each retailer, the manufacturer’s objective function is discontinuous at those points where one of the retailers switches to a different effort level. These critical wholesale price levels, which are summarized in Lemma 4, are potential local extrema and therefore possible solutions to the manufacturer’s optimization problem.

First, we show that a corner solution with $w_{1}=\overline{\overline{w}}$ and $w_{2}<{\bar{w}}$ can never be the optimal solution:

• (i) Suppose that $c\le \frac{se}{4k}[{1-( {1-s})e}]$. Then, $\frac{\partial E{\Pi }_M}{\partial w_1}=\frac{1}{2}({1+e-2kw_1})$, and $\frac{\partial E{\Pi }_M}{\partial w_1}({w_1= \overline{\overline{w}} })=\frac{1}{2}[{-1-({1-s})e+\frac{4ck}{se}}]<0$, if $c<\frac{se}{4k}[{1+({1-s})e}]$. Thus, the manufacturer can earn a higher expected profit by decreasing $w_1$, which is a feasible solution.

• (ii) Suppose that $c>\frac{se}{4k}[{1-( {1-s})e}]$. Then, $\frac{\partial E{\Pi }_M }{\partial w_2}=\frac{1}{2}( {1+e-2kw_2})>0$, if $w_2 <\frac{1+e}{2k}$. Furthermore, ${\bar{w}}<\frac{1+e}{2k}$, if $c>\frac{se}{4k}[{1-({1-s})e}]$. Since $w_2<{\bar{w}}$, the manufacturer can earn a higher expected profit by increasing $w_2$, which is a feasible solution.

Consequently, there remain three critical combinations of wholesale prices, which are depicted in Fig. 7 and described below. Again, we proceed in three steps. First, we derive the conditions under which these points are local maxima. Second, we examine whether each of these points is a potential global extremum or whether it is strictly dominated by some other solution. Third, we compare all potential global extrema to find the solution to the manufacturer’s problem. In Fig. 7, the lines marked A and B refer to the interior solutions described above, where $w_1=w_2=\frac{1+e}{2k},e_1=e_2=e$ (line A) and $w_1=w_2=\frac{1}{2k},e_1 =e_2 =0$ (line B).

The following points of discontinuity are potential local extrema. Again, we restrict the analysis to $w_2={\bar{w}}$ and examine the effects of changes in $w_1$ on the manufacturer’s expected profit since both retailers are assumed to be identical.

• (1) Line $C$: suppose that $w_2={\bar{w}}$. Then, there exists a local maximum in the interval ${\bar{w}}<w_1<\overline{\overline{w}}$ if the condition $\frac{\partial E{\Pi }_M({e_1 =e_2 =e})}{\partial w_1 }=0$ holds for this point. This is true for $w_1 =\frac{1+e}{2k}$ and $\frac{se}{4k}[{1-({1-s})e}]<c<\frac{se}{4k}[{1+( {1-s})e}]$. Both retailers will exert effort and the manufacturer will earn an expected profit denoted by $E{\Pi }_M^3$, which is $E\Pi _M^3 =\frac{1}{8k}[{e^2({1+2s-s^2})+2e({3-s})+1}]-\frac{1}{s^2e^2}\{ {2c^2k-cse[{1-({1-s})e}]}\}$.

• (2) Point $D$: suppose that $w_1={\bar{w}}$ and $w_2={\bar{w}}$. This point is a local maximum if for this combination of wholesale prices the first-order partial derivative of the manufacturer’s profit function with respect to $w_1$ is non-negative, i.e. $\frac{\partial E{\Pi }_M ({e_1=e_2=e})}{\partial w_1 }\ge 0$. This condition is fulfilled for $c\ge \frac{se}{4k}[{1+({1-s})e}]$. We denote the manufacturer’s expected profit for this case by $E{\Pi }_M^4$, and $E{\Pi }_M^4 =\frac{e}{4k}[{se( {2-s})+2}]-\frac{2c}{s^2e^2}( {2ck-se})$.

• (3) Line $E$: suppose that $w_2={\bar{w}}$ and $w_1>\overline{\overline{w}}$. Then, according to Lemma 4 (iv) only Retailer 2 exerts effort. A local maximum is in the interval $w_1>\overline{\overline{w}}$ if for this point $\frac{\partial E{\Pi }_M ({e_1=0,e_2=e})}{\partial w_1}=0$, which is the case for $w_1=\frac{1+({1-s})e}{2k}$ and $c>\frac{se}{4k}({1+e})$. The manufacturer earns an expected profit of $E{\Pi }_M^5$, and $E{\Pi }_M^5=\frac{1}{4k}[{\frac{1}{2}( {e+1})^2-se^2({1-s})+2}]-\frac{c}{s^2e^2}( {2ck-se})$.

Fig. 7

Potential local maxima

Summarizing all of the above, there are different local extrema for each cost level $c$, which are illustrated in Fig. 8.

In order to derive the global maximum, we compare the profits in those cases with more than one local extremum. Note that we can restrict our analysis to $c\le \frac{se}{4k}( {se+2})$ since the manufacturer cannot induce any sales activities for investment costs above this threshold. Thus, the manufacturer will set wholesale prices $w_1=w_2=\frac{1}{2k}$ for $c>\frac{se}{4k}( {se+2})$ and earn an expected profit of $E{\Pi }_M^2$. We begin with $({1-s})e\le 1$ and $\frac{se}{4k}( {e+1})<c\le \frac{se}{4k}({se+2})$, and define the following threshold values $c_1,c_2$, and $c_3$ of $c$:

$$\begin{aligned}&E{\Pi }_M^5 >E{\Pi }_M^2 \Leftrightarrow c<c_1 :=\frac{se}{4k}\left[ {1+\sqrt{e( {2+e})-2se^2( {1-s})} } \right] ;\\&E{\Pi }_M^4 >E{\Pi }_M^2 \Leftrightarrow c<c_2 :=\frac{se}{4k}\left[ {1+\sqrt{se^2( {2-s})+2e} } \right] ;\\&E{\Pi }_M^5 >E{\Pi }_M^4 \Leftrightarrow c>c_3 :=\frac{se}{4k}\left[ {1+\sqrt{2se^2( {3-2s})+e( {2-e})} } \right] . \end{aligned}$$

As $c_1<c_2<c_3$, a point on line $E$, which leads to $E{\Pi }_M^5$, can never be the global optimum because it is always dominated by one of the other two local extrema. The only two points of interest in the whole interval $\frac{se}{4k}({se+1})<c\le \frac{se}{4k}({se+2})$ are $B$ and $D$. The comparison of profits presented above leads to the manufacturer’s optimal decision: the manufacturer should choose point $D$ for $c\le c_2$ and point $B$ for $c>c_2$. It is obvious that the same is true for the case $( {1-s})e>1$, where point $E$ is never a feasible solution to the manufacturer’s problem, since $\frac{se}{4k}( {e+1})>\frac{se}{4k}( {se+2})$.

Fig. 8

Local extrema subject to investment costs

Proof of Proposition 2

• (i) The coordination problem arises for investment costs above the threshold $c>\frac{se}{4k}[{1-( {1-s})e}]$. $\frac{\partial }{\partial s}\frac{se}{4k}[{1-( {1-s})e} ]=\frac{e}{4k}[{({2s-1})e+1}]>0,$ since $s>0.5$. Thus, this threshold value decreases as $s$ decreases.

• (ii) The spread between wholesale prices $\overline{\overline{w}}$ and ${\bar{w}}$ is $\overline{\overline{w}}-{\bar{w}}=\{\frac{1}{k}[{1+( {1-\frac{1}{2}s})e}] -\frac{2c}{se}\}-[{\frac{1}{k}( {1+\frac{1}{2}se})-\frac{2c}{se}}]=({1-s})\frac{e}{k}$. $\frac{\partial }{\partial s}( {1-s})\frac{e}{k}=-\frac{e}{k}<0.$ Therefore the spread between wholesale prices $\overline{\overline{w}}$ and ${\bar{w}}$ increases as $s$ decreases.

• (iii) It is no longer profitable for the manufacturer to induce effort for investment costs above $c>\mathrm{{min}}( {\frac{se}{4k}[{1+\sqrt{se^2( {2-s})+2e}}],\frac{se}{4k}( {se+2})})$. $\frac{\partial }{\partial s}\frac{se}{4k}[{1+\sqrt{se^2( {2-s})+2e}}]=\frac{e}{4k}[{1+\frac{se^2( {3-2s})+2e}{\sqrt{se^2( {2-s})+2e} }}]>0,$ since $s<1$. $\frac{\partial }{\partial s}\frac{se}{4k}({se+2})=\frac{e}{2k}( {se+1})>0.$ Since both arguments in min($\cdot ,\cdot$) increase in $s$, the threshold value min($\cdot ,\cdot$) decreases as $s$ decreases.

Proof of Proposition 3

• (i) Suppose that $c\le \frac{se}{4k}[{1-( {1-s})e} ]$. Then, $d^\mathrm{fr}({s,c})=E{\Pi }_M^{s=1}(c)-E{\Pi }_M ({s,c})=E{\Pi }_M^{s=1} ( c)-E{\Pi }_M^1$. We know from (11) in Lemma 3 that the manufacturer will set $w_1 =w_2 =\frac{1+e}{2k}$. Substituting in (9) we get $q_1=q_2 =\frac{1+e}{4}$ and according to (8), $E{\Pi }_M^{s=1}(c)=\frac{( {1+e})^2}{4k}$. We know from Sect. 4.2 that $E{\Pi }_M^1 =\frac{( {1+e})^2}{4k}$. From this it follows that $d^\mathrm{fr}( {s,c})=\frac{( {1+e})^2}{4k}-\frac{( {1+e})^2}{4k}=0$. Suppose that $c>\frac{e}{4k}[{1+\sqrt{e({e+2})}}]$. Then, $d^\mathrm{fr}( {s,c})=E{\Pi }_M^{s=1} ( c)-E{\Pi }_M ( {s,c})=E{\Pi }_M^{s=1} ( c)-E{\Pi }_M^2$. We know from (13) in Lemma 3 that the manufacturer will set $w_1=w_2=\frac{1}{2k}$. Substituting in (10) we get $q_1=q_2=\frac{1}{4}$ and according to (8), $E{\Pi }_M^{s=1}(c)=\frac{1}{4k}$. We know from Sect. 4.2 that $E{\Pi }_M^2=\frac{1}{4k}$. From this it follows that $d^\mathrm{fr}( {s,c})=\frac{1}{4k}-\frac{1}{4k}=0$.

• (ii) Suppose that $\frac{se}{4k}[{1-( {1-s})e} ]<c\le \frac{se}{4k}[{1+({1-s})e}]$. Then, $d^\mathrm{fr}( {s,c})=E{\Pi }_M^{s=1} ( c)-E{\Pi }_M ( {s,c})=E{\Pi }_M^{s=1} ( c)-E{\Pi }_M^3$. We know from point (i) of this proof that $E{\Pi }_M^{s=1} ( c)=\frac{( {1+e})^2}{4k}$ and from Sect. 4.2 that $E{\Pi }_M^3 =\frac{1}{8k}[{e^2({1+2s-s^2})+2e( {3-s})+1} ]-\frac{1}{s^2e^2}[{2c^2k-cse( {1-( {1-s})e})}]$. It follows that $d^\mathrm{fr}( {s,c})\!=\!\frac{1}{8ks^2e^2}\{{( {s^2e^2\!-\!4ck})^2\!+\!se( {e\!-\!1})[{se( {e\!-\!1})\!-\!2s^2e^2+8ck}]}\}>0$ if $c\!>\!\frac{se}{4k}[{1\!-\!( {1\!-\!s})e}]$. $\frac{\partial d^\mathrm{fr}( {s,c})}{\partial c}\!=\!\frac{se[{({1\!-\!s})e-1}]+4ck}{s^2e^2}>0$ if $c>\frac{se}{4k}[{1- ( {1-s})e}]$. Suppose that $\frac{se}{4k}[{1+({1-s})e}]<c\le \frac{e}{4k}$. Then, $d^\mathrm{fr}( {s,c})=E{\Pi }_M^{s=1} ( c)-E{\Pi }_M ( {s,c})=E{\Pi }_M^{s=1} ( c)-E{\Pi }_M^4$. We know from point (i) of this proof that $E{\Pi }_M^{s=1} ( c)=\frac{( {1+e})^2}{4k}$ and from Sect. 4.2 that $E{\Pi }_M^4 =\frac{e}{4k}[{se( {2-s})+2} ]-\frac{2c}{s^2e^2}( {2ck-se})$. It follows that $d^\mathrm{fr}( {s,c})=\frac{1}{4ks^2e^2}[{({se-4ck})^2+( {1-s})^2s^2e^4}]>0$, while $\frac{\partial d^\mathrm{fr}( {s,c})}{\partial c}=\frac{8ck-2se}{s^2e^2}>0$ if $c>\frac{se}{4k}$. Suppose that $\frac{e}{4k}<c\le \min ( {\frac{se}{4k}[{1+\sqrt{se^2({2-s})+2e} }],\frac{se}{4k}( {se+2})})$. Then, $d^\mathrm{fr}( {s,c})=E{\Pi }_M^{s=1} ( c)-E{\Pi }_M ( {s,c})=E{\Pi }_M^{s=1} ( c)-E{\Pi }_M^4$. We know from (12) in Lemma 3 that the manufacturer will set $w_1 =w_2 =\frac{e+2}{2k}-\frac{2c}{e}$. Substituting in (9) we get $q_1 =q_2 =\frac{1+e}{4}$ and according to (8) $E\Pi _M^{s=1} ( c)=\frac{e^3( {e\!+\!2})\!+\!8cek\!-\!16c^2k^2}{4ke^2}$. It follows that $d^\mathrm{fr}( {s,c})=\frac{1}{4ks^2e^2}[{s^2e^4( {1-s})^2-8ceks( {1-s})+16c^2k^2( {1-s^2})}]>0$ if $c>\frac{e}{4k}$, while $\frac{\partial d^\mathrm{fr}( {s,c})}{\partial c}=\frac{8ck( {1-s^2})-2se( {1-s})}{s^2e^2}>0$, for $c>\frac{e}{4k}$. Suppose that $\min ({\frac{se}{4k}[{1\!+\!\sqrt{se^2( {2\!-\!s})\!+\!2e}} ],\frac{se}{4k}({se\!+\!2})})\!<\!c\!\le \frac{e}{4k}[{1\!+\!\sqrt{e( {e\!+\!2})} } ]$. Then, $d^\mathrm{fr}( {s,c})\!=\!E\Pi _M^{s\!=\!1} ( c)\!-\!E\Pi _M ( {s,c})=E\Pi _M^{s=1} ( c)-E\Pi _M^2$. We know from the above that $E\Pi _M^{s=1} (c)=\frac{e^3({e+2})+8cek-16c^2k^2}{4ke^2}$ and from Sect. 4.2 that $E{\Pi }_M^2 =\frac{1}{4k}$. It follows that $d^\mathrm{fr}( {s,c})=\frac{8ck( {e-2ck})+e^2( {e^2+2e-1})}{4ke^2}$, while$\frac{\partial d^\mathrm{fr}( {s,c})}{\partial c}=\frac{2e-8ck}{e^2}<0$ if $c>\frac{e}{4k}$.

• (iii) First, we show that the manufacturer’s expected profit does not increase as $s$ decreases. We showed in Proposition 2 that in this case all threshold values from Proposition 1 decrease.

  $E{\Pi }_M^1$ and $E{\Pi }_M^2$ are independent of $s$: $\frac{\partial E\Pi _M^1 }{\partial s}=\frac{\partial E\Pi _M^2 }{\partial s}=0$.

  $E{\Pi }_M^3$ and $E{\Pi }_M^4$ decrease as $s$ decreases:

  $\frac{\partial E\Pi _M^3 }{\partial s}=\frac{1}{4ks^3e^2}\{ {s^3e^3[{({1-s})e-1}]+4ck[{se( {e-1})+4ck}]}\}>0,$ if $c>\frac{se}{4k}[{1-( {1-s})e}]$,

  $\frac{\partial E\Pi _M^4 }{\partial s}=\frac{1}{2ks^3e^2}[ {s^3e^4( {1-s})+4ck({4ck-se})}]>0,$ if $c>\frac{se}{4k}$.

  Since the manufacturer’s expected profit $E{\Pi }_M ({s,c})$ either decreases or does not change as $s$ decreases and $E{\Pi }_M^{s=1} (c)$ does not depend on $s$, the difference $d^\mathrm{fr}({s,c})=E\Pi _M^{s=1} (c)-E\Pi _M ({s,c})$ increases or does not change as $s$ decreases.

  The same is true for $d^\mathrm{tot}( {s,c})=E\Pi _M^\mathrm{FB} ( c)-E\Pi _M ( {s,c})$, since the first best solution $E\Pi _M^\mathrm{FB} ( c)$ does not depend on $s$.