Delay-induced oscillations in Wilson and Cowan’s model: an analysis of the subthalamo-pallidal feedback loop in healthy and parkinsonian subjects

Abstract

The model proposed by Wilson and Cowan (1972) describes the dynamics of two interacting subpopulations of excitatory and inhibitory neurons. It has been used to model neural structures like the olfactory bulb, whisker barrels, and the subthalamo-pallidal system. It is well-known that this system can exhibit an oscillatory behavior that is amplified by the presence of delays. In the absence of delays, the conditions for stability are well-known. The aim of our paper is to clarify these conditions when delays are included in the model. The first ingredient of our methods is a new necessary and sufficient condition for the existence of multiple equilibria. This condition is related to those for local asymptotic stability. In addition, a sufficient condition for global stability is also proposed. The second and main ingredient is a stability analysis of the system in the frequency-domain, based on the Nyquist criterion, that takes the four independent delays into account. The methods proposed in this paper can be applied to analyse the stability of the subthalamo-pallidal feedback loop, a deep brain structure involved in Parkinson’s disease. Our stability conditions are easy to compute and characterize sharply the system’s parameters for which spontaneous oscillations appear.

Appendices

Appendix A: Proof of Theorem 1

Proof of Lemma 1 Denote by $I$ the interval $\left[\,0,1\right]$. And, for $\alpha \in \{ e, i \}$, define $I_\alpha = \{ x \in \mathbb R ^2 : x_\alpha \in I\}$. By Hypothesis 1, the activation functions satisfy $0 \le S_\alpha (x) \le 1$, for each $x \in \mathbb R$. Therefore, if $x_\alpha \le 0$ then $\dot{x}_\alpha \ge 0$, and if $x_\alpha \ge 1$ then $\dot{x}_\alpha \le 0$. Now, define $V_\alpha (x)$ as the square of the distance between $x$ and the set $I_\alpha$. We have, for $\alpha \in \{ e, i \}$,

$$\begin{aligned} V_\alpha (x)=\left\{ \begin{array}{cl} (x_\alpha -1)^2 \quad&\text{ if} x_\alpha \ge 1, \\ 0 \quad&\text{ if} 0 \le x_\alpha \le 1, \text{ and} \\ x_\alpha ^2 \quad&\text{ if} x_\alpha \le 0. \end{array} \right. \end{aligned}$$

(32)

On the one hand, the function $V_\alpha (x)$ is differentiable and $\dot{V}_\alpha (x)\le 0$. But, on the other hand, we have $I_\alpha = \{ x \in \mathbb R ^2 : V_\alpha (x) \le 0 \}$. These two properties imply that $I_\alpha$ is positively invariant (Khalil (2002), Sect. 4.2).

Now, observe that $D=I_e \cap I_i$. Since the intersection of two positively invariant sets is itself positively invariant (Bhatia and Szegö (1970), Theorem II.1.2), it follows that the unit square $D$ is positively invariant (independently of the values of the delays and of the external inputs). That is, if the state of the system enters the set $D$ at some instant $t_0$, then it will remain in $D$ for all $t \ge t_0$ (Fig. 10). $\square$

Fig. 10

The three different cases of Theorem 1. The activation functions $S_e$ and $S_i$ are those of the subthalamopallidal loop Nevado-Holgado et al. (2010), re-scaled in order to satisfy Hypothesis 1. For them $\sigma _e=\sigma _i=1$. In all cases, we took $c_{ie} = c_{ei} = c_{ii} = 1$, and changed $c_{ee}$. A For $c_{ee} = 0.875$, the case (i) applies and the equilibrium is unique. B For $c_{ee} = 1.625$, the case (iii) applies and there are always multiple equilibria, independently of the level of inhibition. C For $c_{ee} = 1.375$, the case (ii) applies and the equilibrium is unique when external inhibition is low. D But, when the level of external inhibition is high enough, multiple equilibria are also possible

Proof of Theorem 1 First step. For any pair of constant inputs $(u_e^*,u_i^*)$, consider the two nullclines

$$\begin{aligned} N_e&= \left\{ (x_e,x_i) \in \mathbb R ^2 : x_e = S_e \left( c_{ee}\,x_e - c_{ie}\,x_i + u_e^*\right) \right\} \end{aligned}$$

(33)

$$\begin{aligned} N_i&= \left\{ (x_e,x_i) \in \mathbb R ^2 : x_i = S_i \left( c_{ei}\,x_e - c_{ii}\,x_i + u_i^*\right) \right\} \!. \end{aligned}$$

(34)

All equilibria $(x_e^*,x_i^*)$ of Eqs. (1) and (2) are located on the set $N_e \cap N_i$. That is, they satisfy simultaneously the two equations

$$\begin{aligned} x_e^*&= S_e \left( c_{ee}\,x_e^*- c_{ie}\,x_i^*+ u_e^*\right)\end{aligned}$$

(35)

$$\begin{aligned} x_i^*&= S_i \left( c_{ei}\,x_e^*- c_{ii}\,x_i^*+ u_i^*\right). \end{aligned}$$

(36)

Observe that these equations do not depend on the system’s delays. Since

$$\begin{aligned} N_e \subset \left\{ (x_e,x_i) \in \mathbb R ^2 : x_e \in [ 0,1 ] \right\} \quad \text{ and} \quad N_i \subset \left\{ (x_e,x_i) \in \mathbb R ^2 : x_i \in [ 0,1 ] \right\} , \end{aligned}$$

it follows that all equilibria belong to the unit square.

Second step. Using the inverse activation functions $T_\alpha$ defined above, the nullclines can also be described by

$$\begin{aligned} N_e&\!= \left\{ (x_e,x_i) \in \mathbb R ^2 : x_i \!=\! \frac{1}{c_{ie}} \left( c_{ee}\,x_e \!-\! T_e(x_e) \!+\! u_e^*\right) \right\} \end{aligned}$$

(37)

$$\begin{aligned} N_i&\!= \left\{ (x_e,x_i) \in \mathbb R ^2 : x_e \!=\! \frac{1}{c_{ei}} \left( c_{ii}\,x_i \!+\! T_i(x_i) \!-\! u_i^*\right) \right\} . \end{aligned}$$

(38)

It was observed by Wilson and Cowan that there is an asymmetry between these two sets: unlike $N_e$, the set $N_i$ can always be described as the graph of a strictly increasing function, defined on the interval $[ 0, 1 ]$. That is

$$\begin{aligned} x_e = \varphi ( x_i, u_i^*), \quad \forall x \in [ 0, 1 ], \end{aligned}$$

where

$$\begin{aligned} \varphi (x_i,u_i^*) = \frac{1}{c_{ei}} \left( c_{ii}\,x_i + T_i(x_i) - u_i^*\right). \end{aligned}$$

Using the fact that for each $u_i^*$ the function $\varphi$ is both surjective and strictly increasing on the interval $[ 0, 1 ]$, we can define $x_i^a(u_i^*)$ and $x_i^b(u_i^*)$ as the only solutions of the equations

$$\begin{aligned} \frac{1}{c_{ei}} \left( c_{ii}\,x_i^a + T_i(x_i^a) - u_i^*\right) = 0 \end{aligned}$$

and

$$\begin{aligned} \frac{1}{c_{ei}} \left( c_{ii}\,x_i^b + T_i(x_i^b) - u_i^*\right) = 1, \end{aligned}$$

respectively. Observe that a point $(x_e,x_i)$ is an equilibrium if and only if $x_i$ belongs to the interval $[ x_i^a, x_i^b ]$ and satisfies the equation

$$\begin{aligned} x_i = \frac{1}{c_{ie}} \left( c_{ee}\,\varphi ( x_i, u_i^*) - T_e(\varphi ( x_i, u_i^*)) + u_e^*\right). \end{aligned}$$

Third step. We are now able to define, for each $x \in [ x_i^a, x_i^b ]$, the functions

$$\begin{aligned}&H(x) = \frac{1}{c_{ie}} \left( c_{ee}\,\varphi ( x, u_i^*) - T_e(\varphi ( x, u_i^*)) + u_e^*\right) \quad \text{ and}\nonumber \\&\quad L(x) = H(x) - x. \end{aligned}$$

By construction, a point $(x_e,x_i)$ is an equilibrium if and only if

$$\begin{aligned} L(x_i)=0. \end{aligned}$$

(39)

Moreover, in any of the three cases described by the theorem, the function $L$ is such that

$$\begin{aligned} \lim \limits _{x \rightarrow {x_i^a}^+} L(x) = +\infty \quad \text{ and} \quad \lim \limits _{x \rightarrow {x_i^b}^-} L(x) = -\infty . \end{aligned}$$

(40)

Since this function is continuous then, necessarily (by the intermediate value theorem), it must vanish on $( x_i^a, x_i^b )$.

If we omit the dependency of these functions on $u_i^*$, the derivative of $L$ can be computed using the chain rule

$$\begin{aligned} L^\prime (x) = \dfrac{1}{c_{ie}} \left( c_{ee}\,\varphi ^\prime (x) - T_e^\prime (\varphi (x)) \varphi ^\prime (x) \right) - 1, \end{aligned}$$

where

$$\begin{aligned} \varphi ^\prime (x) = \dfrac{1}{c_{ei}} \left( c_{ii} + T_i^\prime (x) \right). \end{aligned}$$

Grouping the factors of $\varphi ^\prime (x)$ in $L(x)$ leads to

$$\begin{aligned} L^\prime (x) = \dfrac{1}{c_{ie}c_{ei}} \left( c_{ee} - T_e^\prime (\varphi (x)) \right) \left( c_{ii} + T_i^\prime (x) \right) - 1. \end{aligned}$$

By Hypothesis 1, this function is continuous at each point for which it is defined.

Claim 1

For a given $u_i^*$, assume that there exists $x_i^*$ such that $L^\prime (x_i^*)>0$. Then, there exists $u_e^*$ such that the system admits at least three distinct equilibria.

Proof of Claim 1 On the one hand, since $L^\prime (x_i^*)>0$, there exists an interval $[x_i^c,x_i^d] \subset [x_i^a,x_i^b]$ such that $x_i^*\in (x_i^c,x_i^d)$ and $L^\prime (x)>0$ for each $x \in [x_i^c,x_i^d]$. Additionally, we can chose $u_e^*$ such that $L(x_i^*)=0$. Hence, we can assume that $L(x_i^c)<0$ and $L(x_i^d)>0$. But, on the other hand, it follows from (40) that there exist two points $x_i^e$ and $x_i^f$ such that $x_i^a < x_i^e < x_i^c$ and $x_i^d < x_i^f < x_i^b$, for which $L(x_i^e)>0$ and $L(x_i^f)<0$. Therefore, by the continuity of $L$ and by the intermediate value theorem, there exist two points $x_j^*$ and $x_k^*$ such that $x_j^*\in [x_i^e,x_i^c]$ and $x_j^*\in [x_i^d,x_i^f]$, and that satisfy, respectively, the equations $L(x_j^*) = 0$ and $L(x_k^*) = 0$. $\square$

Fourth step. Using the previous result, we can continue with the proof of Theorem 1 and treat, one after the other, its three cases.

Item (i). The first case appears when $\sigma _e c_{ee} \le 1$. In this case $c_{ee} - T_e^\prime (\varphi (x)) \le 0$ because $T_e^\prime \ge 1/\sigma _e$. Since $c_{ii} + T_i^\prime (x) \ge 1/\sigma _i \ge 0$, we must have $L^\prime (x)<0$, for each $x \in ( x_i^a, x_i^b )$. The uniqueness of the equilibrium point comes from the fact that $L$ is strictly decreasing. Its existence is guaranteed by the intermediate value theorem and by the limits of $L$ at each end of its domain (40).

Item (ii). This case could be proved using the geometric argument proposed in (Wilson and Cowan (1972), Theorem 1). Nevertheless, for the sake of completeness, we give here an alternative proof. In this case it must be shown that, when $\sigma _e c_{ee} > 1$, there always exist $u_i^*$ and a point $x^*$ such that $L^\prime (x^*)>0$. To this end, for a given $u_i^*$, we look for a point $x^*$ such that $T_e(\varphi (x^*))=1/\sigma _e$. That is, such that $\varphi (x^*) = y^*$, where $y^*$ is a point at which $T_e$ reaches its minimum $1/\sigma _e$. The existence of $y^*$ is guaranteed by Hypothesis 2. The existence of $x^*$ comes from the injectivity of $\varphi$. In other words, the equation

$$\begin{aligned} \frac{1}{c_{ei}} \left( c_{ii}\,x + T_i(x) - u_i^*\right) = y^* \end{aligned}$$

(41)

always admits a unique solution $x^*$ in $( x_i^a, x_i^b )$. Moreover, rewriting the solution of Eq. (41) as

$$\begin{aligned} c_{ii}\,x^*+ T_i(x^*) = c_{ei} y^*+ u_i^*\end{aligned}$$

and computing the limit of the right side, we obtain

$$\begin{aligned} \lim \limits _{u_i^*\rightarrow +\infty } c_{ii}\,x^*+ T_i(x^*) = \lim \limits _{u_i^*\rightarrow +\infty } c_{ei}\,y^*+ u_i^*= +\infty . \end{aligned}$$

This necessarily implies that

$$\begin{aligned} \lim \limits _{u_i^*\rightarrow +\infty } x^*(u_i^*) = 1. \end{aligned}$$

Now, combining the equality

$$\begin{aligned} c_{ee} - T_e^\prime (\varphi (x^*)) = c_{ee} - \dfrac{1}{\sigma _e} \end{aligned}$$

with the limit

$$\begin{aligned} \lim \limits _{u_i^*\rightarrow +\infty } c_{ii} + T_i^\prime (x^*) = +\infty , \end{aligned}$$

we have, for $u_i^*$ big enough, that

$$\begin{aligned} \left( c_{ee} - T_e^\prime (\varphi (x^*)) \right) \left( c_{ii} + T_i^\prime (x^*) \right) > c_{ie} c_{ei}. \end{aligned}$$

For such an $u_i^*$, we have $L^\prime (x^*)>0$. Hence, by Claim 1, in this case there are at least three distinct equilibria.

Item (iii). For the third case, observe that the relation

$$\begin{aligned} \left( c_{ee} - \frac{1}{\sigma _e} \right) \left( c_{ii} + \frac{1}{\sigma _i} \right) > c_{ie} c_{ei} \end{aligned}$$

is satisfied if and only if

$$\begin{aligned} c_{ee} > \frac{1}{\sigma _e} + \dfrac{c_{ie} c_{ei}}{c_{ii} + \frac{1}{\sigma _i}}. \end{aligned}$$

Therefore, the condition imposed by this case is more restrictive than that of the previous one. The key point of the proof is to be able to find, for each fixed $u_i^*$, a point $x^*$ such that $L^\prime (x^*)>0$.

On the one hand, we have

$$\begin{aligned} c_{ii} + T_i^\prime (x) \ge c_{ii} + \frac{1}{\sigma _i}, \end{aligned}$$

for each $x \in (0,1)$. On the other hand, by Hypothesis 2, there is always a point on which $T^\prime _e$ reaches its minimum $1/\sigma _e$. Define $y^*$ to be this point. Now, take the only $x^*$ such that $\varphi (x^*,u_i^*)=y^*$. This is always possible because $\varphi$ is both surjective and strictly increasing, for each $u_i^*$. Hence,

$$\begin{aligned} L^\prime (x^*)&= \dfrac{1}{c_{ie} c_{ei}}\left( c_{ee} - \frac{1}{\sigma _e} \right) \left( c_{ii} + T_i^\prime (x^*) \right) - 1 \\&\ge \dfrac{1}{c_{ie} c_{ei}}\left( c_{ee} - \frac{1}{\sigma _e} \right) \left( c_{ii} + \frac{1}{\sigma _i} \right) - 1 \\&> 0 \end{aligned}$$

Since we have $L^\prime (x^*)>0$, the proof of this last case of the theorem follows from Claim 1. $\Box$

Appendix B: Proof of Theorem 2

Proof of Lemma 2 Taking a first-order Taylor expansion of $S_e$ and combining it with Eq. (35), leads to the following computation :

$$\begin{aligned} \tau _e\,\dot{z}_e&= \tau _e\,\dot{x}_e - \tau _e\,\dot{x}_e^*\\&= -x_e(t) + S_e \left( c_{ee} x_e(t-\delta _{ee}) - c_{ie} x_i(t-\delta _{ie}) + u_e \right) \\&= -(z_e(t)+x_e^*) + S_e \left( c_{ee} x_e^*- c_{ie} x_i^*+ u_e^*\right) + \\ +&S^\prime _e \left( c_{ee} x_e^*- c_{ie} x_i^*+ u_e^*\right) \cdot \left( c_{ee} z_e(t-\delta _{ee}) - c_{ie} z_i(t-\delta _{ie}) + p_e \right) \\&{+ o(\left\Vert z \right\Vert^2)} \\&= -z_e(t) + \sigma _e^*\left( c_{ee} z_e(t-\delta _{ee}) - c_{ie} z_i(t-\delta _{ie}) + p_e \right)\\&+{o(\left\Vert z \right\Vert^2)}, \end{aligned}$$

which gives with linearized dynamics (4). Taking a first-order Taylor expansion of $S_i$ and combining it with Eq. (36) leads, after a similar computation, to Eq. (5)$.\square$

Proof of Proposition 1 Item (i). By the Hartman and Grobman Theorem, the local asymptotic stability or instability of the original system can be deduced from that of the linearized system, provided that for this last system there are no eigenvalues on the imaginary axis (Guckenheimer and Holmes (1983). Theorem 1.3.1)

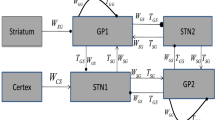
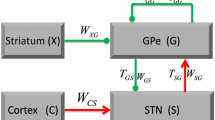
For the linearized system, when all delays are equal to zero, working in the frequency-domain we can define the transfer functions

$$\begin{aligned} H_e(s) = \dfrac{c_{ei}}{\dfrac{\tau _e}{\sigma _e^*}s + \dfrac{1}{\sigma _e^*} - c_{ee}} \quad \text{ and} \quad H_i(s) = \dfrac{c_{ie}}{\dfrac{\tau _i}{\sigma _i^*}s + \dfrac{1}{\sigma _i^*} + c_{ii}} \end{aligned}$$

(42)

that appear in the block diagram of Figure 1. Define also the numerators and denominators of these transfer functions by $H_e(s) = N_e(s)/M_e(s)$ and $H_i(s) = N_i(s)/M_i(s)$. It follows from standard results of feedback control theory (Doyle et al. (1992), Sect. 3.2) that the feedback system of Figure 1 is input-output stable if and only if the roots of

$$\begin{aligned}&N_e(s)N_i(s) + M_e(s) M_i(s)=\nonumber \\&\dfrac{\tau _e \tau _i}{\sigma _e^*\sigma _i^*} s^2 + \left( -\dfrac{\tau _i}{\sigma _i^*} \left( c_{ee} - \frac{1}{\sigma _e^*} \right) + \dfrac{\tau _e}{\sigma _e^*}\left( c_{ii} + \frac{1}{\sigma _i^*} \right) \right) s \nonumber \\&- \left( c_{ee} - \frac{1}{\sigma _e^*} \right)\left( c_{ii} + \frac{1}{\sigma _i^*} \right) + c_{ei}c_{ie} \end{aligned}$$

(43)

have a strictly negative real part. By Routh’s criterion (Ogata (2001), Sect. 5.5) this happens if and only if all the coefficients of this polynomial are strictly positive. This last point ends the proof, since the input-output stability of the feedback loop implies the exponential stability of the linearized system (Curtain and Zwart (1995). Theorem 7.3.2)

Item (ii). First step. With a slight abuse of notation, we define $f_e=(-x_e+S_e)/\tau _e$ and $f_i=(-x_i+S_i)/\tau _i$. That is, we omit the arguments of these two functions, which leads to $\dot{x}_e = f_e$ and $\dot{x}_i = f_i$. Now, define

$$\begin{aligned} V = \dfrac{\tau _e}{2} f_e^2 + \dfrac{\tau _i}{2} f_i^2. \end{aligned}$$

(44)

We have

$$\begin{aligned} \dot{V}&= -f_e^2 + c_{ee} S_e^\prime f_e^2 - c_{ie} S_e^\prime f_e f_i -f_i^2\nonumber \\&\quad + c_{ei} S_i^\prime f_e f_i - c_{ii} S_e^\prime f_i^2\nonumber \\&= (c_{ee} S_e^\prime -1) f_e^2 + (-c_{ii} S_i^\prime -1) f_i^2 \nonumber \\&\quad +\left( c_{ei} S_i^\prime - c_{ie} S_e^\prime \right) f_e f_i. \end{aligned}$$

(45)

Second step. In order to show that the time-derivative of $V$ is negative one can use Young’s inequality, which states that for any real numbers $a$ and $b$ we have

$$\begin{aligned} ab \le \frac{a^2}{2} + \frac{b^2}{2}. \end{aligned}$$

Using this inequality and the fact that $S_\alpha ^\prime \le \sigma _\alpha$, gives the following bound

$$\begin{aligned} c \, S_\alpha ^\prime \, f_e f_i&\le c \, S_\alpha ^\prime \, \frac{1}{2} \left( f_e^2 + f_i^2 \right) \\&\le c \, \sigma _\alpha \, \frac{1}{2} \left( f_e^2 + f_i^2 \right). \end{aligned}$$

Injecting this last inequality in Eq. (45) leads to

$$\begin{aligned}&\dot{V} \le (c_{ee} S_e^\prime -1) f_e^2 + (-c_{ii} S_i^\prime -1) f_i^2 \nonumber \\&\quad + \frac{1}{2} \left( c_{ie} \sigma _e + c_{ei} \sigma _i \right) \left( f_e^2 + f_i^2 \right). \end{aligned}$$

Since $0 \le S_e^\prime \le \sigma _e$ and $S_i^\prime \ge 0$, this expression can be simplified further to

$$\begin{aligned} \dot{V} \le (c_{ee} \sigma _e-1) f_e^2 - f_i^2 + \frac{1}{2} \left( c_{ie} \sigma _e + c_{ei} \sigma _i \right) \left( f_e^2 + f_i^2 \right).\nonumber \\ \end{aligned}$$

(46)

Third step. Observe that the two conditions (8) of Proposition 1, together, imply that there exists a real number $\epsilon >0$ such that

$$\begin{aligned} \frac{1}{2}\left( c_{ei} \sigma _i + c_{ie} \sigma _e \right) = \left( 1 - c_{ee} \sigma _e \right) - \epsilon . \end{aligned}$$

Combining this last expression with inequality (46) leads directly to

$$\begin{aligned} \dot{V} \le -\epsilon \left( f_e^2 + f_i^2 \right). \end{aligned}$$

Now, by Theorem 1, the first part of condition (8) implies the uniqueness of the equilibrium point, which is then the only point for which $V(x_e,x_i)=0$. It follows that $V$ is a Lyapunov function that satisfies the standard conditions for global asymptotic stability (Khalil (2002), Theorem 4.1). $\square$

Proof of Lemma 3 In order to prove Item (i) we can assume that $c_{ee} \ne 0$ because, otherwise, the result is trivial. Now, the first point is to observe that if $c_{ee}> 1/\sigma _e^*$ then $H_e$ is unstable when $\delta _{ee}=0$. The fact that $H_e$ remains unstable when $\delta _{ee}{>}0$ results directly from Nyquist’s criterion (Curtain and Zwart (1995). Theorem 9.1.8) Indeed, since $G_e$ has no unstable poles, the stability of $H_e$ imposes that the Nyquist locus of $G_e$ must not encircle the critical point. But, when $c_{ee}> 1/\sigma _e^*$, it is easy to show that the Nyquist locus of $G_e$ encircles the critical point when $\delta _{ee}=0$. Increasing $\delta _{ee}=0$ can only increase the number of encirclements. This case is illustrated in Figure 11A. If follows that $H_e$ is unstable when $c_{ee} > 1/\sigma _e^*$, independently of the value of $\delta _{ee}\ge 0$. When $c_{ee} < 1/\sigma _e^*$, the result follows directly from the small-gain theorem (Curtain and Zwart (1995). Theorem 9.1.7) In this last case, the stability does not depend on the value of $\delta _{ee}\ge 0$. This case is illustrated in Figure 11B.

Fig. 11

Nyquist diagrams associated with the four different cases of Lemma 3

In order to prove Item (ii) we can assume that $c_{ii} \ne 0$, like in the case of Item (i). We can observe, moreover, that $H_i$ is always stable when $\delta _{ii}=0$. When $c_{ii}<1/\sigma _e^*$, then the stability of $H_i$ results from the small-gain theorem and does not depend on the value of $\delta _{ii}\ge 0$. This case is illustrated in Figure 11D. While, when $c_{ii}>1/\sigma _e^*$, the delay-margin of the system is well defined and can be computed analytically. Nyquist’s criterion implies that the system is stable if and only if $\delta _{ii}< \Delta (H_i)$. This last case, which is illustrated in Figure 11C, ends the Proof of Lemma 3. $\square$

Proof of Lemma 4 We can assume that $c \ne 0$, since otherwise the result is trivial. Define $D(s) = 1/H(s)$. Our aim is to prove that $\gamma _D$ is strictly increasing. We have

$$\begin{aligned} D(j\omega ) = a j \omega + b + c e^{-j \omega d}. \end{aligned}$$

Therefore, using Euler’s formula, we obtain

$$\begin{aligned} D(j\omega )&= a j \omega + b + c \left( \cos (d\omega ) - j \sin (d \omega ) \right) \\&= \left( b + c \cos (d\omega ) \right) + \left( a \omega - c\sin (d\omega ) \right) j \end{aligned}$$

and thus

$$\begin{aligned} | D(j\omega ) |^2 = \left( b + c \cos (d\omega ) \right)^2 + \left( a \omega - c\sin (d\omega ) \right)^2. \end{aligned}$$

Now, define $f(\omega )=\frac{1}{2}| D(j\omega ) |^2$. We have

$$\begin{aligned} f^{\prime }(\omega )&= \left( b + c \cos (d\omega ) \right)\left( -cd \sin (d\omega ) \right) \nonumber \\&+ \left( a \omega - c\sin (d\omega ) \right)\left( a - cd\cos (d\omega ) \right), \end{aligned}$$

which simplifies to

$$\begin{aligned} f^{\prime }(\omega ) = a^2\omega - a c d \omega \cos (d\omega ) - a c \sin (d\omega ) - b c d \sin (d\omega ). \end{aligned}$$

Using the fact that $-1 \le \cos (d\omega ) \le 1$ and that $-d\omega \le \sin (d\omega ) \le d\omega$, one can obtain the bounds $-a c d \omega \cos (d \omega ) \ge -a |c| d \omega$, $-b c d \sin (d \omega ) \ge -b |c| d^2 \omega$, and $-a c \sin (d \omega ) \ge -a |c| d \omega$. These bounds lead to the inequality

$$\begin{aligned} f^{\prime }(\omega ) \ge \left( a^2 - b |c| d^2 - 2 a |c| d \right) \omega . \end{aligned}$$

We can therefore conclude that the relation

$$\begin{aligned} d + \dfrac{b}{2a}\,d^2 < \dfrac{a}{2 |c|} \end{aligned}$$

implies $f^{\prime }(\omega ) \ge 0$, for $\omega \ge 0$. In this case $\gamma _D$ is strictly increasing and, thus, $\gamma _H$ strictly decreasing, which ends the proof of Lemma 4. $\square$

Proof of Theorem 2 First step. The first assumption of the theorem, on the exponential stability of $H_e$ and $H_i$, implies that the open-loop transfer $G$ has neither poles nor zeros with a positive real part. We can thus apply Nyquist’s criterion in its simplest form (Curtain and Zwart (1995), Theorem 9.1.8). To this end, define the Nyquist locus $\Gamma (\delta )$ as the image of the imaginary axis by the complex map $\exp (-s\delta ) G(s)$, where $\delta =\delta _{ei}+\delta _{ie}$ is the total delay in the loop. In other words,

$$\begin{aligned} \Gamma (\delta ) = \left\{ e^{-j\omega \delta }G(j\omega ), \quad \text{ for} \omega \in \mathbb R \right\} . \end{aligned}$$

(47)

In our case, Nyquist’s criterion states that the stability of the closed-loop system is obtained if and only if $\Gamma (\delta )$ does not encircle the critical point $-1$.

Second step. The second assumption of the theorem is that the loop gain $\gamma _G$ is strictly decreasing. If $\gamma _G(0) \le 0$ then $\Delta (G)=+\infty$ and the system is stable independently of the value of the loop delays. In this case, the small-gain theorem (Curtain and Zwart (1995) Theorem 9.1.7) can be used, as an alternative, to prove the system’s stability. When the small-gain condition is not satisfied, that is when $\gamma _G(0)> 0$, then the system has a well-defined delay margin $\Delta (G)$. Indeed, in this case, the crossover frequency $\omega _G$ can be computed numerically as the only solution of the equation $\gamma _G(\omega _G)=0$ and, by definition,

$$\begin{aligned} \Delta (G) = \frac{\pi -\varphi _G(\omega _G)}{\omega _G}. \end{aligned}$$

In order to know if the Nyquist locus $\Gamma (\delta )$ encircles the critical point, one must consider its intersection

$$\begin{aligned} P(\delta )=e^{-j\omega _G\delta }G(j\omega _G) \end{aligned}$$

with the unit circle. The encirclement of the critical point is avoided only if $P(\delta )$ has a strictly negative imaginary part.

Third step. Observe that if $\Delta (G) \le 0$ then $\Gamma (0)$ encircles the critical point. In this case, the system is unstable for any $\delta \ge 0$. In other words, the system is unstable independently of the value of the total loop delay. Now, the last case that remains to be handled is when $0<\Delta (G)<+\infty$. But, in this case, the Nyquist contour $\Gamma (\delta )$ encircles or passes through the critical point if and only if $\delta \ge \Delta (G)$. Therefore, the system is exponentially stable if and only if the loop delay satisfies $\delta < \Delta (G)$, which ends the proof of Theorem 2$.\square$