Vector strength after Goldberg, Brown, and von Mises: biological and mathematical perspectives

Abstract

The vector strength, a number between 0 and 1, is a classical notion in biology. It was first used in neurobiology by Goldberg and Brown (J Neurophys 31:639–656, 1969) but dates back at least to von Mises (Phys Z 19:490–500, 1918). It is widely used as a means to measure the periodicity or lack of periodicity of a neuronal response to an outside periodic signal. Here, we provide a self-contained and simple treatment of a closely related notion, the synchrony vector, a complex number with the vector strength as its absolute value and with a definite phase that one can directly relate to a biophysical delay. The present analysis is essentially geometrical and based on convexity. As such it does two things. First, it maps a sequence of points, events such as spike times on the time axis, onto the unit circle in the complex plane so that for a perfectly periodic repetition, a single point on the unit circle appears. Second, events hardly ever occur periodically, so that we need a criterion of how to extract periodicity out of a set of real numbers. It is here where convex geometry comes in, and a geometrically intuitive picture results. We also quantify how the events cluster around a period as the vector strength goes to 1. A typical example from the auditory system is used to illustrate the general considerations. Furthermore, von Mises’ seminal contribution to the notion of vector strength is explained in detail. Finally, we generalize the synchrony vector to a function of angular frequency, not fixed on the input frequency at hand and indicate its potential as a “resonating” vector strength.

Appendices

Appendix A: Convex geometry

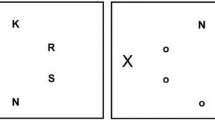
For any real linear vector space such as the two-dimensional plane ${\mathbb{R }}^2$ (or, equivalently, the complex plane), we have been working with all the time, a set is convex if for every pair of points $P$ and $Q$ within the set every point on the straight-line segment that joins them is also within the set. The set in Fig. 2a is clearly convex since for any pair of points $P$ and $Q$, i.e., vectors $\mathbf x _{P}$ and $\mathbf x _{Q}$, the line segment of convex combinations $p_{1} \mathbf x _{P} +p_{2} \mathbf x _{Q}$ with $p_{j} \ge 0$ and $p_{1} + p_{2} =1$ is also in this set. Since $p_{1} = 1 - p_{2}$, we can write the convex combination as $\mathbf x _{P} +p_{2} (\mathbf x _{Q} - \mathbf x _{P})$ with $0 \le p_{2} \le 1$, so that we have a line segment connecting $P$ and $Q$. On the other hand, the set in Fig. 2b is not convex since the dashed part of the line connecting $P$ and $Q$ is outside the set.

Fig. 2

The geometry of convexity looks harmlessly simple, but its consequences are deep (Kelly and Weiss 1979; Klee 1971; Roberts and Varberg 1973; van Tiel 1984). a For a convex set ${\fancyscript{C}}$ each line segment connecting two points $P$ and $Q$ in ${\fancyscript{C}}$ is contained itself in ${\fancyscript{C}}$. Since the line segment is only defined in a vector space such as the two-dimensional plane in a–c, we need to assume a vector (to be precise, affine Gallier 2001; Kelly and Weiss 1979) space to start with. Plainly, the set in b is not convex since the dashed part of the line segment connecting $P$ and $Q$ is not in the set. In c, we have the closed unit disk $x^2 + y^2 \le 1$ with the unit circle $x^2 + y^2 = 1$ or, alternatively, for complex numbers $z = x + iy$ with $|z| = 1$ as boundary. The unit disk is convex and the unit circle consists of extreme points only. That is, any $z = \exp (i \phi )$ on the unit circle cannot be written as a convex combination $p_{1} \mathbf x _{P} +p_{2} \mathbf x _{Q}$ with $\mathbf x _{P}$ and $\mathbf x _{Q}$ in the unit disk and both $p_{j} > 0$. In c, we take the barycenter $[\exp ( i \phi _{1}) + \exp ( i \phi _{2})]/2$ for the synchrony vector (10) with $n=2$. Plainly, the barycenter is now inside the unit disk

For any $n \ge 2$ vectors $\mathbf x _{j}$ with $1 \le j \le n$ in a convex set ${\fancyscript{C}}$ the convex combination $\sum _{j} p_{j} \mathbf x _{j}$ with $p_{j} \ge 0$ and $\sum _{j} p_{j} =1$ is also in ${\fancyscript{C}}$. The proof is by induction. We start with $n=2$ and note that with $\mathbf x _{1}$ and $\mathbf x _{2} \in {\fancyscript{C}}$ there is nothing to prove. Let us therefore assume the statement is correct up to and including $n \ge 3$ and show

$$\begin{aligned} \sum _{j=1}^{n+1} p_{j} \mathbf x _{j} \in {\fancyscript{C}} \ . \end{aligned}$$

(23)

To this end we write

$$\begin{aligned} \sum _{j=1}^{n+1} p_{j} \mathbf x _{j} \!=\! (1-p_{n+1}) \, \sum _{j=1}^{n} \frac{p_{j}}{(1\!-\!p_{n+1})} \mathbf x _{j} \!+\! p_{n+1} \mathbf x _{n+1}. \end{aligned}$$

(24)

Because we have started with a convex combination, we have $\sum _{1}^{n+1} p_{j} = 1$. By induction, the sum on the right in (24) is in ${\fancyscript{C}}$ since

$$\begin{aligned} p_{j} \ge 0 \quad \mathrm{and} \quad \sum _{j=1}^{n} \frac{p_{j}}{(1-p_{n+1})} = 1. \end{aligned}$$

(25)

In (10) we have taken all $p_{j} = 1/n$ for $1 \le j \le n$. If the resultant barycenter $(\sum _{j} \mathbf x _{j})/n$ has its absolute value near $1$, then the “cloud” of the $\{ \mathbf{x}_{j}, 1\le j \le n\}$ must be pretty small. It is bound to approach the unit circle as $|(\sum _{j} \mathbf x _{j})/n| \rightarrow 1$ as a consequence of the convex geometry.

The closed unit disk $\{ |z| \le 1\}$ in Fig. 2c is convex and the unit circle $\{ |z| = 1\}$ consists of extreme points of the (closed) convex unit disk. That is, any $z = \exp (i \phi )$ on the unit circle is an extreme point (Kelly and Weiss (1979), §5.3) since it cannot be written $p_{1} \mathbf x _{P} +p_{2} \mathbf x _{Q}$ with $\mathbf x _{P}$ and $\mathbf x _{Q}$ in the unit disk and both $p_{j} > 0$. In other words, either $p_{1}$ or $p_{2} =0$, and the convex combination reduces to the extreme point itself. There is an old theorem due to Minkowski saying that any vector $\mathbf x$ in a compact convex set ${\fancyscript{C}}$ can be written as a finite convex combination of extreme points of ${\fancyscript{C}}$. A sharpening due to Carathéodory states that in $\mathrm{I\!R}^{n}$ at most $n+1$ extreme points already do the job; for a triangle ($n=2$) the three corners indeed are sufficient.

The convex set ${\fancyscript{C}}$ is called a simplex if the preceding decomposition is unique for all its points. A triangle is a simplex, but a glance at Fig. 2c shows that the unit disk is not. Just pick a point $P$ in its interior and draw a bundle of lines through $P$, i.e., the vector $\mathbf x _{P}$, all of which cut the unit circle in two points $\mathbf x _{1}$ and $\mathbf x _{2}$. We can then write $\mathbf x _{P} = p_{1} \mathbf x _{1} +p_{2} \mathbf x _{2}$ with $p_{1} + p_{2} = 1$ and $p_{j} >0$ as soon as $P \leftrightarrow \mathbf x _{P}$ is in the interior of the unit disk. Kelly and Weiss (1979) nicely explain convex geometry while Klee (1971) gives a great overview. Van Tiel (1984) presents a succinct, slick introduction to convex analysis. Roberts and Varberg (1973) provide a wealth of clearly explained details to those who want to know how the mathematics of convexity works precisely, while Simon (2011) is good for a splendid and truly elegant exposition of the associated analytics, but sometimes on a much higher level.

Fig. 3

Vector strength as proposed by von Mises (1918) a Top left: specific weights (i.e., weights per unit volume) of 18 metallic elements and three alloys (Kanonengut $=$ gunmetal, Messing $=$ brass, and Stahl $=$ steel). Top right: atomic weights of the 24 lightest elements w.r.t. hydrogen. Whereas the latter agree nicely with the integrity hypothesis (see main text), the former do not. b Bottom left: synchrony vector $\rho$ as plotted by von Mises for period $T=1$ and $\omega = 2\pi$ corresponding to the integrity of the specific weights one wants to verify (or disprove). The numbers next to the bars signaling the specific $\exp (2\pi i \, t_{j})$ indicate their frequency of occurrence. The vector strength for the left column of the table in a turns out to be $r = |\rho |= 0.168$, corresponding to the length of the vector $\rho$ with endpoint $S$. Clearly, there is no sign of periodicity, neither in the left column nor according to the synchrony vector $\rho$. c Bottom right: in contrast to b, for the atomic weights of the 24 lightest elements their synchrony vector $\rho$ with endpoint $S$ and $r = |\rho |= 0.765$ exhibits integrity. In fact, by using the representation $\exp (2\pi i\, t_{j})$ on the unit circle von Mises had also taken into account another phenomenon: most of the time the $t_{j}$ “skip” quite a few positive integers, but it makes no difference to the plot. All figures are due to von Mises (1918, Tables I and II, Figs. 2 and 3, §5; $\copyright$ Hirzel-Verlag) and appeared more than half a century before Goldberg and Brown’s classic (1969)

Appendix B: Von Mises (1918) verifying periodicity of experimental data

By the end of the First World War, Richard von Mises, an Austrian who was professor of applied mathematics in Strasbourg (Alsace) but in those days served as an airplane builder in the Austro-Hungarian army (he even developed a “Mises airplane,” which—in German, nomen est omen—was never put into production as it was too big for the available motors), apparently had some spare moments to ponder the following fascinating problem. It was the time of the Bohr model of atoms, and science had noticed that the (dimensionless) atomic weights compared to hydrogen (H) had a remarkable resemblance to the natural numbers, the positive integers; cf. the right column of Fig. 3a, a reproduction taken from von Mises’ 1918 paper. Its manuscript was received on 14 July and published in the famous Physikalische Zeitschrift (Physical Journal) on 15 November 1918, four days after Armistice Day, the end of the “Great War.”

As announced in the title of his paper, “On the ‘integrity’ of the atomic weights and related problems,” what von Mises (1918, §2) was trying to explain is evident when we focus on, e.g., the right column of Fig. 3a, a list of the 24 lightest elements with their atomic weights. The weights resemble positive integers pretty well. Question: How well? Is this by accident and, if not, what is the corresponding probability? Von Mises’ argument was, and our present argument is, that in the case of a periodic phenomenon of period $T=1$ we need to put things on a circle, viz., $\exp (i \omega t)$ with $\omega = 2\pi /T = 2\pi$, where after one walk around we are automatically back where we started. Surprisingly, von Mises argued so without any further ado as early as 1918.

Hence, we turn to (10), first compute $\rho$ for the specific (nonatomic) weights of 21 metals as spike times $t_{j}$, just numbers on the real axis ${\mathbb{R }}$, and compare them with the supposed periodicity 1. That is, for the angular frequency $\omega = 2 \pi /T$ with $T=1$ we obtain $[\sum _{j=1}^{n} \exp (2 \pi i t_{j})]/n$ with $n=21$, where the $t_{j}$ are the specific weights of 18 metallic elements plus three alloys, distracters that nevertheless nicely focus on the disagreement with periodicity, all shown explicitly in the left column of Fig. 3a. Von Mises (1918, Fig. 3, §5) found $r = |\rho |= 0.168$, as depicted in Fig. 3b, and concluded that integrity is highly improbable, which we cannot help but agree with. On the other hand, for the atomic weights of the $n=24$ lightest elements appearing in the right column of Fig. 3a we find $r = |\rho |= 0.765$ as shown in Fig. 3c, also due to von Mises’ original paper ((von Mises 1918, Fig. 2, §5)). We conclude that here integrity is highly probable, whereas equidistribution is to be rejected.

In summary, what von Mises did was to use the synchrony vector (10) with its absolute value, the vector strength, as a criterion for quickly checking the amount of periodicity present in data and, at the same time, to devise a statistic, the so-called von Mises distribution, to test the integrity or periodicity of atomic weights; cf. Fig. 3.