Fixed-point bifurcation analysis in biological models using interval polynomials theory

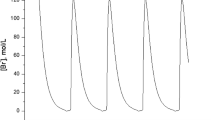
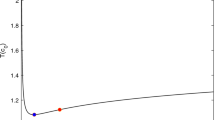
Abstract

The paper proposes a systematic method for fixed-point bifurcation analysis in circadian cells and similar biological models using interval polynomials theory. The stages for performing fixed-point bifurcation analysis in such biological systems comprise (i) the computation of fixed points as functions of the bifurcation parameter and (ii) the evaluation of the type of stability for each fixed point through the computation of the eigenvalues of the Jacobian matrix that is associated with the system’s nonlinear dynamics model. Stage (ii) requires the computation of the roots of the characteristic polynomial of the Jacobian matrix. This problem is nontrivial since the coefficients of the characteristic polynomial are functions of the bifurcation parameter and the latter varies within intervals. To obtain a clear view about the values of the roots of the characteristic polynomial and about the stability features they provide to the system, the use of interval polynomials theory and particularly of Kharitonov’s stability theorem is proposed. In this approach, the study of the stability of a characteristic polynomial with coefficients that vary in intervals is equivalent to the study of the stability of four polynomials with crisp coefficients computed from the boundaries of the aforementioned intervals. The efficiency of the proposed approach for the analysis of fixed-point bifurcations in nonlinear models of biological neurons is tested through numerical and simulation experiments.

Appendices

Appendix

A Stability analysis through the Routh–Hurwitz criterion

Since the Routh–Hurwitz criterion is meanwhile of the category well known but not widely known, a quick look at the ideas will be taken behind this classical method and a few concrete examples will be analyzed as illustrations of how to apply it.

The Routh–Hurwitz criterion provides a systematic method for finding out if all the roots of a polynomial lie in the left complex semi-plane. In the case of a dynamical system described in the s-frequency domain by a transfer function, one can find if the denominator’s characteristic polynomial contains only stable roots thus concluding that the system is also stable. Moreover, one can find out the number of complex eigenvalues which lie in the right complex semi-plane and thus are unstable. Additionally, one can find if there are roots of the polynomial with purely imaginary part, resulting a sustained oscillations dynamics (limit cycles).

1.1 The Routh–Hurwitz stability criterion

To evaluate the stability of the roots of the characteristic polynomial

$$\begin{aligned} p(\lambda )={a_n}\lambda ^n+{a_{n-1}}\lambda ^{n-1}+\cdots +{a_1}{\lambda }+{a_0} \end{aligned}$$

(77)

the following Routh table is considered:

$$\begin{aligned} \begin{array}{cccccc} s^n &{} | &{} a_n &{} a_{n-2} &{} a_{n-4} &{} \cdots \\ s^{n-1} &{} | &{} a_{n-1} &{} a_{n-3} &{} a_{n-5} &{} \cdots \\ s^{n-2} &{} | &{} {q_1}^{(n-2)} &{} {q_2}^{(n-2)} &{} {q_3}^{(n-2)} &{} \cdots \\ s^{n-3} &{} | &{} {q_1}^{(n-3)} &{} {q_2}^{(n-3)} &{} {q_3}^{(n-3)} &{} \cdots \\ \cdots &{} | &{} \cdots &{} \cdots &{} \cdots &{} \cdots \\ s^{1} &{} | &{} q_1^{(1)} &{} q_2^{(1)} &{} &{} \\ s^{0} &{} | &{} q_1^{(0)} &{} &{} &{} \end{array} \end{aligned}$$

(78)

where

$$\begin{aligned} \begin{array}{cc} q_1^{(n-2)}=-\frac{\text {det}\begin{pmatrix} a_n &{} a_{n-2} \\ a_{n-1} &{} a_{n-3} \end{pmatrix}}{a_{n-1}} &{} q_2^{(n-2)}=-\frac{\text {det}\begin{pmatrix} a_n &{} a_{n-4} \\ a_{n-1} &{} a_{n-4} \end{pmatrix}}{a_{n-1}} \\ q_1^{(n-3)}=-\frac{det\begin{pmatrix} a_{n-1} &{} a_{n-3} \\ q_1^{(n-2)} &{} q_2^{(n-2)} \end{pmatrix}}{{q_1}^{(n-2)}} &{} q_2^{(n-3)}=-\frac{det\begin{pmatrix} a_{n-1} &{} a_{n-4} \\ q_1^{(n-2)} &{} q_3^{(n-2)} \end{pmatrix}}{{q_1}^{(n-2)}} \end{array} \end{aligned}$$

(79)

etc.

The Routh–Hurwitz stability analysis points out that the number of unstable roots of the characteristic polynomial (roots with positive real part) is equal to the number of changes of sign appearing in the first column of the Routh table.

Example 1

The characteristic polynomial $p(s)=s^4+5s^3+20s^2+30s+40$ is considered. The associated Routh table is

$$\begin{aligned} \begin{array}{cccc} s^4 \ | &{} 1 &{} 20 &{} 40 \\ s^3 \ | &{} 5 &{} 30 &{} 0 \\ s^2 \ | &{} 14 &{} 40 &{} 0 \\ s^1 \ | &{} 15.714 &{} 0 &{} \\ s^0 \ | &{} 40 &{} &{} \\ \end{array} \end{aligned}$$

(80)

No change of sign is observed in the first column of the Routh table. Therefore, the characteristic polynomial has no roots in the right complex semi-plane and is a stable one.

Example 2

The characteristic polynomial $p(s)=s^3+2s^2+4s+30$ is considered. The associated Routh table is

$$\begin{aligned} \begin{array}{ccc} s^3 \ | &{} 1 &{} 4 \\ s^2 \ | &{} 2 &{} 30 \\ s^1 \ | &{} -11 &{} 0 \\ s^0 \ | &{} 30 &{} \end{array} \end{aligned}$$

(81)

There are two changes if sign in the first column of the Routh table; therefore, the characteristic polynomial has two unstable roots.

Example 3

The characteristic polynomial $p(s)=s^5+2s^4+3s^3+6s^2+12s+18$ is considered. In this case, an element in the first column of the Routh table becomes equal to 0. This is substituted by a small positive number $\epsilon$. Next, the sign of the elements of the first column of the Routh table is examined while $\epsilon {\rightarrow }0$. Thus, the associated Routh table becomes

$$\begin{aligned} \begin{array}{cccc} s^5 \ | &{} 1 &{} 3 &{} 12\\ s^4 \ | &{} 2 &{} 6 &{} 18\\ s^3 \ | &{} \epsilon &{} 3 &{} 0\\ s^2 \ | &{} 6-\frac{6}{\epsilon } &{} 18 &{} 0\\ s^1 \ | &{} \frac{18\epsilon -18-18\epsilon ^2}{6\epsilon -6} &{} 0 &{} 0\\ s^0 \ | &{} 18 &{} &{} \\ \end{array} \end{aligned}$$

(82)

For ${\epsilon }{\rightarrow }0^{+}$, the elements of the first column become $1,2,\epsilon >0,6-\frac{6}{\epsilon }<0,3,18$. There are two changes of sign in the elements of the first column of Routh table, and consequently, there are two unstable roots in the right complex semi-plane.

Example 4

The characteristic polynomial $p(s)=s^5+6s^4+10s^3+35s^2+24s+44$ is considered. In such a case, complete row of the associated Routh table can become equal to zero. This happens when among the roots of the characteristic polynomial there are conjugate imaginary ones or complex roots of opposite sign. To process this case, an auxiliary characteristic polynomial is generated using the row that precedes the row where zeroing appeared. By dividing the initial characteristic polynomial with the auxiliary characteristic polynomial, one obtains a new characteristic polynomial for which the computation of the Routh table is repeated.

The Routh table of the initial characteristic polynomial is

$$\begin{aligned} \begin{array}{cccc} s^5 \ | &{} 1 &{} 10 &{} 24\\ s^4 \ | &{} 6 &{} 35 &{} 44\\ s^3 \ | &{} \frac{25}{6} &{} \frac{50}{3} &{} 0\\ s^2 \ | &{} 11 &{} 44 &{} 0\\ s^1 \ | &{} 0 &{} 0 &{} 0\\ s^0 \ | &{} &{} &{} \\ \end{array} \end{aligned}$$

(83)

The auxiliary characteristic polynomial is $p(s)=11s^2+44$ with purely imaginary roots $s_{1,2}={\pm }j2$. The new characteristic polynomial is computed using $q(s)=p(s)/a(s)=s^3+6s^2+6s+11$. For $q(s)$, the Routh table is

$$\begin{aligned} \begin{array}{ccc} s^3 \ | &{} 1 &{} 6\\ s^2 \ | &{} 6 &{} 11 \\ s^1 \ | &{} \frac{25}{6} &{} 0 \\ s^0 \ | &{} 11 &{} \\ \end{array} \end{aligned}$$

(84)

For the new Routh table, there is no change of sign in its first column; thus, all roots of $q(s)$ lie in the left complex semi-plane. Consequently, for the initial characteristic polynomial, it holds $p(s)=(11s^2+44)q(s)$ which means that $p(s)$ has two purely imaginary roots (Hopf bifurcations) while the rest of its roots are stable.

Example 5

Consider the characteristic polynomial $p(s)=s^6+2s^5+9s^2+12s^3+43s^2+50s+75$. The associated Routh table is

$$\begin{aligned} \begin{array}{ccccc} s^6 \ | &{} 1 &{} 9 &{} 43 &{} 75\\ s^5 \ | &{} 2 &{} 12 &{} 50 &{} 0\\ s^4 \ | &{} 3 &{} 18 &{} 75 &{} 0\\ s^3 \ | &{} 0 &{} 0 &{} 0 &{} 0\\ s^2 \ | &{} &{} &{} &{} \\ s^1 \ | &{} &{} &{} &{} \\ s^0 \ | &{} &{} &{} &{} \\ \end{array} \end{aligned}$$

(85)

There is zeroing of one row. The auxiliary characteristic polynomial is formulated using the row preceding to zeroing, that is $a(s)=3s^4+18s^3+75=3(s^4+6s^2+25)$. By diving the initial characteristic polynomial with the auxiliary characteristic polynomial, the new characteristic polynomial is obtained. That is

$$\begin{aligned} q(s)&= {\frac{{p(s)}}{{a(s)}}}={\frac{1}{3}}(s^2+2s+3){\Rightarrow }\nonumber \\ p(s)&= {\frac{1}{3}}(s^2+2s+3)(s^4+6s^2+25) \end{aligned}$$

(86)

The polynomial $q_1(s)=s^4+6s^2+25$ has complex roots (every two of them are opposite to each other), that is $\rho _1=1+j2$, $\rho _2=1-j2$, $\rho _3=-1+j2$ and $\rho _4=-1-j2$. The polynomial $q_2(s)=s^2+2s+3$ has the complex conjugate roots $\rho _1=-1+j\sqrt{2}$ and $\rho _2=-1-j\sqrt{2}$. From the previous analysis, it can be seen that the characteristic polynomial $p(s)$ has roots in the right complex semi-plane and is unstable.

1.2 Use of the Routh–Hurwitz criterion for the computation of relative stability

By performing the change of variable $s{\rightarrow }p-a$ in the characteristic polynomial, one can find the relative position of the roots of the characteristic polynomial with respect to a reference value. This means that one can conclude if the roots of the characteristic polynomial are located to the left of the reference eigenvalue $a$ (they decay faster than $a$) or to the right of the reference eigenvalue (they decay slower than $a$).

The following characteristic polynomial is considered: $p(s)=s^3+10.2{s^2}+21s+2$ and the associated Routh table becomes

$$\begin{aligned} \begin{array}{ccc} s^3 \ | &{} 1 &{} 21 \\ s^2 \ | &{} 10.2 &{} 2 \\ s^1 \ | &{} 20.804 &{} 0 \\ s^0 \ | &{} 2 \end{array} \end{aligned}$$

(87)

The system has the following stable poles $p_1=-7.39$, $p_2=-2.70$, $p_3=-0.10$. It is examined if the poles of the system decay faster than the eigenvalue, $a=-0.2$. The change of variables $s=p-0.2$ or $p=s+0.2$ is considered. The new characteristic polynomial is $q(s)=p^3+9.6{p^2}+16.32p-1.728$ and the associated Routh table becomes

$$\begin{aligned} \begin{array}{ccc} p^3 \ | &{} 1 &{} 16.32 \\ p^2 \ | &{} 9.6 &{} -1.728 \\ p^1 \ | &{} 16.580 &{} 0 \\ p^0 \ | &{} -1.732 \end{array} \end{aligned}$$

(88)

It can be noticed that there is one change of sign in the first column of the Routh table; therefore, the characteristic polynomial has an eigenvalue which lies to the right of the reference eigenvalue $a=-0.2$.