Constrained Minimum Passage Time in Random Geometric Graphs

Abstract

Let $G$ be a random geometric graph formed by $n$ nodes with adjacency distance $r_n$ and let each edge of $G$ be assigned an independent exponential passage time with mean that depends on the graph size $n.$ We connect $G$ to two nodes source $s_A$ and destination $s_B$ at deterministic locations spaced $d_n$ apart in the unit square and find upper and lower bounds on the minimum passage time between $s_A$ and $s_B$ through paths in $G$ having constant stretch, i.e., whose length is constrained to be proportional to the Euclidean distance between $s_A$ and $s_B.$

Appendices

Appendix 1: Edge weight assigments

Let $\{W_{j_1,j_2,j_3}\}_{j_1,j_2,j_3 \ge 1}$ be i.i.d. random variables with cumulative distribution function (cdf) $F_n$ that are also independent of the node locations $\{X_i\}.$ We first describe edge weight assignments and then discuss the conditional independence property.

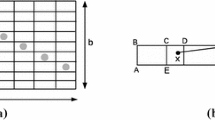
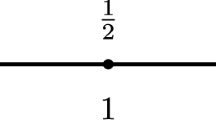
Edge weight assignments To assign weights to the edges of the random graph $G$ from the set $\{W_{j_1,j_3,j_4}\},$ we follow an analogous procedure as in Chapter $1$ of Meester and Roy [10]. The basic idea is to first assign each node $X_j,$ a unique pair of positive integers $m(X_j) := (q,l_j).$ Next if $X_i$ and $X_j$ are joined by an edge $(X_i,X_j)$ in $G,$ then we define the passage time $t(X_i,X_j) := W_{q,l_i,l_j}.$ The integer pair $(q,l_j)$ is obtained by dividing the unit square $S$ into successively finer subsquares of size $\frac{1}{2^{q}}, q \ge 1$ each, until each subsquare contains at most one node of $\{X_i\}.$

Formally, for $k \ge 1$ divide the unit square $S$ into disjoint $\frac{1}{2^{k}} \times \frac{1}{2^{k}}$ squares $\{S_{k,l}\}_{1 \le l \le 2^{2k}}.$ Let $q$ be the smallest integer such that each square in $\{S_{q,l}\}$ contains at most one node of $\{X_i\}.$ If node $X_j$ is present in square $S_{q,l_j},$ we then set $m(X_j) := (q,l_j).$

We illustrate the above procedure in Fig. 3, where the unit square $ABCD$ is first subdivided into $4$ subsquares each of side length $\frac{1}{2}.$ This partition is not fine enough since the square $AEFG$ contains two nodes $x$ and $y.$ Further subdividing $\frac{1}{2} \times \frac{1}{2}$ subsquare into $4$ subsquares each, we get a fine enough partition so that each subsquare contains at most one node.

Conditional independence property We use the following conditional independence property throughout. For any measurable function $g = g(X_1,\ldots ,X_n)$ and any $i \ne j,$ we have

$$\begin{aligned} .&{\mathbb {P}}(t(X_i,X_j)< x, g< y) \nonumber \\&\;\;\;=\;\;\sum _{q,l_i,l_j} {\mathbb {P}}(t(X_i,X_j)< x, g< y,m(X_i) = (q,l_i), m(X_j) = (q,l_j)) \nonumber \\&\;\;\;= \;\;\sum _{q,l_i,l_j} {\mathbb {P}}(W_{q,l_i,l_j}< x, g< y, m(X_i) = (q,l_i), m(X_j) = (q,l_j)) \nonumber \\&\;\;\;= \;\;\sum _{q,l_i,l_j} {\mathbb {P}}(W_{q,l_i,l_j}< x) {\mathbb {P}} (g< y, m(X_i) = (q,l_i), m(X_j) = (q,l_j)) \nonumber \\&\;\;\;= \;\;F_n(x) \sum _{q,l_i,l_j} {\mathbb {P}} (g< y, m(X_i) = (q,l_i), m(X_j) = (q,l_j)) \nonumber \\&\;\;\;= \;\;F_n(x) {\mathbb {P}} (g < y). \end{aligned}$$

(A1.1)

We then say that given the node locations $\{X_i\},$ the passage times $\{t(X_i,X_j)\}$ are independent in the sense of (A1.1).

Fig. 3

Subdividing the unit square into fine subsquares until each subsquare contains at most one node

Appendix 2: Deviation estimates

We use the following deviation estimate throughout. Let $\{R_j\}_{1 \le j \le m}$ be independent Bernoulli random variables with 

$$\begin{aligned} p_j = {\mathbb {P}}(R_j = 1) = 1-{\mathbb {P}}(R_j = 0) > 0 \end{aligned}$$

and let $R = \sum _{j=1}^{m} R_j.$ If $p_{low} \le p_j \le p_{up}$ for all $1 \le j \le m$ then then

$$\begin{aligned} {\mathbb {P}}\left( \frac{mp_{low}}{2} \le R \le 2mp_{up} \right) \ge 1-4\exp \left( -\frac{mp_{low}}{16}\right) \end{aligned}$$

(A2.1)

for all $m \ge 1.$

Proof of (A2.1): Letting $\mu = {\mathbb {E}}R$ and $0 < \epsilon \le \frac{1}{2},$ we have from Corollary A.1.14, pp. 312 of [1] that

$$\begin{aligned} {\mathbb {P}}\left( \left| R - \mu \right| \ge \mu \epsilon \right) \le 2\exp \left( -C(\epsilon )\mu \right) \end{aligned}$$

(A2.2)

where $C(\epsilon ) = \min \left( \frac{\epsilon ^2}{2}, -\epsilon + (1+\epsilon )\log (1+\epsilon )\right) \ge \frac{\epsilon ^2}{4}$ because $\log (1+\epsilon ) > \epsilon - \frac{\epsilon ^2}{2}$ and so 

$$\begin{aligned} -\epsilon + (1+\epsilon )\log (1+\epsilon ) \ge -\epsilon + (1+\epsilon )\left( \epsilon - \frac{\epsilon ^2}{2}\right) = \frac{\epsilon ^2}{2} - \frac{\epsilon ^3}{2} \ge \frac{\epsilon ^2}{4}, \end{aligned}$$

since $0 < \epsilon \le \frac{1}{2}.$ Setting $\epsilon = \frac{1}{2}$ we therefore get

$$\begin{aligned} {\mathbb {P}}(R \ge 2mp_{up}) \le {\mathbb {P}}\left( X \ge \frac{3\mu _m}{2}\right) \le 2e^{-\mu _m/16} \le 2e^{-mp_{low}/16} \end{aligned}$$

and an analogous analysis holds for the lower bound. $\square$

Let $R_1,\ldots ,R_m$ be independent exponential random variables with mean $\lambda$ and let $R = \sum _{j=1}^{m} R_j$ so that ${\mathbb {E}}R = m\lambda .$ We then have

$$\begin{aligned} {\mathbb {P}}\left( R \le 2m\lambda \right) \ge 1-e^{-m/6} \end{aligned}$$

(A2.3)

and

$$\begin{aligned} {\mathbb {P}}\left( R \ge m\frac{\log (1+\lambda )}{2}\right) \ge 1-\exp \left( -m\frac{\log (1+\lambda )}{2}\right) \end{aligned}$$

(A2.4)

Proof of (A2.3): For $s < \frac{1}{\lambda },$ we have ${\mathbb {E}}e^{sR_i} = \lambda ^{-1}\int _{0}^{\infty }e^{sx}e^{-x\lambda ^{-1}} = \frac{1}{1-s\lambda }.$ Therefore

$$\begin{aligned} {\mathbb {P}}\left( R \ge 2m\lambda \right) \le e^{-2sm\lambda } {\mathbb {E}}e^{sR} \le e^{-2sm\lambda } \left( \frac{1}{1-s\lambda }\right) ^{m} = e^{-\delta m}, \end{aligned}$$

where $\delta = 2s\lambda + \log \left( 1-s\lambda \right) .$ If $s\lambda = \frac{1}{3},$ then

$$\begin{aligned} |\log (1-s\lambda )| = \sum _{k \ge 1} \frac{(s\lambda )^{k}}{k} \le \sum _{k \ge 1} (s\lambda )^{k} = \frac{s\lambda }{1-s\lambda } = \frac{1}{2} \end{aligned}$$

and so $\delta = \frac{1}{6}$ and consequently, ${\mathbb {P}}(R \ge 2m\lambda ) \le e^{-m/6}.$

For the lower bound, we let $s > 0$ and get 

$$\begin{aligned} {\mathbb {E}}e^{-sR_i} = \lambda ^{-1}\int _{0}^{\infty }e^{-sx}e^{-x\lambda ^{-1}} = \frac{1}{1+s\lambda }. \end{aligned}$$

For $x > 0$ we therefore have

$$\begin{aligned} {\mathbb {P}}\left( R \le mx\right) \le e^{smx} {\mathbb {E}}e^{-sR} \le e^{smx} \left( \frac{1}{1+s\lambda }\right) ^{m} = e^{-\theta m}, \end{aligned}$$

where $\theta = \log (1+s\lambda ) - sx.$ Setting $s=1$ and $x = \frac{\log (1+\lambda )}{2}$ we get (A2.4).  $\square$