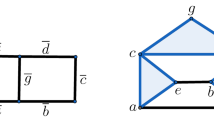
Morse Theory and Evasiveness

M

is a non-contractible subcomplex of a simplex S then M is evasive. In this paper we make this result quantitative, and show that the more non-contractible M is, the more evasive M is. Recall that M is evasive if for every decision tree algorithm A there is a face of S that requires that one examines all vertices of S (in the order determined by A) before one is able to determine whether or not lies in M. We call such faces evaders of A. M is nonevasive if and only if there is a decision tree algorithm A with no evaders. A main result of this paper is that for any decision tree algorithm A, there is a CW complex M', homotopy equivalent to M, such that the number of cells in M' is precisely

where the constant is +1 if the emptyset is not an evader of A, and -1 otherwise. In particular, this implies that if there is a decision tree algorithm with no evaders, then M is homotopy equivalent to a point. This is the theorem in [12].

In fact, in [12] it was shown that if M is non-collapsible then M is evasive, and we also present a quantitative version of this more precise statement.

The proofs use the discrete Morse theory developed in [6].