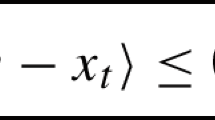Abstract
An online policy learning problem of linear control systems is studied. In this problem, the control system is known and linear, and a sequence of quadratic cost functions is revealed to the controller in hindsight, and the controller updates its policy to achieve a sublinear regret, similar to online optimization. A modified online Riccati algorithm is introduced that under some boundedness assumption leads to logarithmic regret bound. In particular, the logarithmic regret for the scalar case is achieved without boundedness assumption. Our algorithm, while achieving a better regret bound, also has reduced complexity compared to earlier algorithms which rely on solving semi-definite programs at each stage.




Similar content being viewed by others
References
Akbari M, Gharesifard B, Linder T (2020) “Riccati updates for online linear quadratic control,” In proceedings of the 2nd conference on learning for dynamics and control, vol. 120, pp. 476–485, PMLR
Agarwal A, Hazan E, Kale S, Schapire RE (2006) “Algorithms for portfolio management based on the Newton method,” In proceedings of the 23rd international conference on machine learning, ICML ’06, pp. 9–16
Luo H, Wei C, Zheng K (2018) “Efficient online portfolio with logarithmic regret,” In Advances in neural information processing systems 31, pp. 8235–8245, Curran Associates, Inc
Patel M, Ranganathan N (2001) IDUTC: an intelligent decision-making system for urban traffic-control applications. IEEE Trans Vehicular Technol 50(3):816–829
Zhai J, Li Y, Chen H (2016) “An online optimization for dynamic power management,” In 2016 IEEE international conference on industrial technology (ICIT), pp. 1533–1538
Anava O, Hazan E, Mannor S, Shamir O (2013) “Online learning for time series prediction,” in proceedings of the 26th annual conference on learning theory, vol. 30, pp. 172–184
Ross S, Gordon G, Bagnell D (2011) “A reduction of imitation learning and structured prediction to no-regret online learning,” In proceedings of the fourteenth international conference on artificial intelligence and statistics, pp. 627–635
Cesa-Bianchi N, Lugosi G (2006) Prediction, learning, and games. Cambridge University Press, Cambridge
Hazan E (2016) Introduction to online convex optimization. Foundation Trends Optim 2(3–4):157–325
Shalev-Shwartz S (2012) Online Learning and Online Convex Optimization, vol. 12 of Foundations and Trends in Machine Learning. Now Publishers Inc
Hazan E, Agarwal A, Kale S (2007) Logarithmic regret algorithms for online convex optimization. Mach Learn 69(2–3):169–192
Hazan E, Kale S (2014) Beyond the regret minimization barrier: optimal algorithms for stochastic strongly-convex optimization. J Mach Learn Res 15(1):2489–2512
Gofer E, Cesa-Bianchi N, Gentile C, Mansour Y (2013) “Regret minimization for branching experts,” In conference on learning theory, pp. 618–638
Blum A, Mansour Y (2007) From external to internal regret. J Mach Learn Res 8:1307–1324
Cohen A, Hasidim A, Koren T, Lazic N, Mansour Y, Talwar K (2018) “Online linear quadratic control,” In proceedings of the 35th international conference on machine learning, vol. 80, pp. 1029–1038
Agarwal N, Bullins B, Hazan E, Kakade S, Singh K (2019) “Online control with adversarial disturbances,” In proceedings of the 36th international conference on machine learning, vol. 97, pp. 111–119
Agarwal N, Hazan E, Singh K (2019) “Logarithmic regret for online control,” http://arxiv.org/abs/1909.05062
Foster D, Simchowitz M (2020) “Logarithmic regret for adversarial online control,” In proceedings of the 37th international conference on machine learning, vol. 119, pp. 3211–3221, PMLR
Garcia CE, Prett DM, Morari M (1989) Model predictive control: theory and practice; a survey. Automatica 25(3):335–348
Yu H, Neely M, Wei X (2017) Online convex optimization with stochastic constraints. Adv Neural Inf Process Syst 30:1428–1438
Neely, MJ, Yu H (2017) “Online convex optimization with time-varying constraints,” http://arxiv.org/abs/1702.04783
Jenatton R, Huang J, Archambeau C (2016) “Adaptive algorithms for online convex optimization with long-term constraints,” In proceedings of the 33rd international conference on machine learning, vol. 48, pp. 402–411
Sutton RS, Barto AG (2018) Reinforcement learning: an introduction. The MIT Press, Cambridge
Yang Y, Guo Z, Xiong H, Ding D, Yin Y, Wunsch DC (2019) Data-driven robust control of discrete-time uncertain linear systems via off-policy reinforcement learning. IEEE Trans Neural Netw Learn Syst 2:87
Karimi A, Kammer C (2017) A data-driven approach to robust control of multivariable systems by convex optimization. Automatica 85:227–233
Hall EC, Willett RM (2015) Online convex optimization in dynamic environments. IEEE J Select Top Signal Process 9(4):647–662
Hewer G (1971) An iterative technique for the computation of the steady state gains for the discrete optimal regulator. IEEE Trans Autom Control 16(4):382–384
Caines PE, Mayne DQ (1970) On the discrete time matrix Riccati equation of optimal control. Int J Control 12(5):785–794
Akbari M, Gharesifard B, Linder T (2020) “On the lack of monotonicity of Newton-Hewer updates for Riccati equations,” http://arxiv.org/abs/2010.15983
Soderstrom T (2002) Discrete-time stochastic systems: estimation and control, 2nd edn. Springer-Verlag, New York
Bertsekas DP (2018) Stable optimal control and semicontractive dynamic programming. SIAM J Control Optim 56(1):231–252
Rodman L, Lancaster P (1995) Algebraic Riccati Equations. Oxford Mathematical Monographs
Balakrishnan V, Vandenberghe L (2003) Semidefinite programming duality and linear time-invariant systems. IEEE Trans Autom Control 48(1):30–41
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Published in the topical collection Machine Learning for Control Systems and Optimal Control
Research supported in part by a grant from the Natural Sciences and Engineering Research Council of Canada. An incomplete version of this paper was presented at the 2nd Conference on Learning for Dynamics and Control (L4DC) and has appeared as [1].
Appendix
Appendix
Proposition A.1
Let \(n=m=1\) and let \(\{P_t\}_{t=1}^T\) be a sequence of positive numbers generated by Equation (3.1) and (3.2) recursively, and assume that policy \(K_t\) is stabilizing for all \(t\ge 1\). Then there exists \(\nu >0\) such that \(P_t\le \nu \) for all \(t\ge 1\).
Proof
Note that
Since \(K_t\) is stabilizing using the stability of \(K_1\), c.f. Lemma 4, we have that
Now if you consider \(P_t\) as a function of \(K_t\), by taking derivative of \(P_t\) with respect to \(K_t\) and setting it to zero, we have that
minimizes the \(P_t\) and the minimum admissible \(P_t\) which we denote by \({\tilde{P}}_t\) is given by
Now if we write \(P_{t+1}\) as a function of \(P_t\) we have that
By taking derivative of \(P_{t+1}\) with respect to \(P_t\), we conclude that for the admissible \(P_t\), i.e., \(P_t\ge {\tilde{P}}_t\), the function \(P_{t+1}\) is decreasing for \(P_t\le \breve{P}_t\) and increasing for \(P_t\ge \breve{P}_t\) [29], where \(\breve{P}_t\) is given by
Since \(P_{t+1}\) is decreasing for \(P_t\le \breve{P}_t\) and increasing for \(P_t\ge \breve{P}_t\), its maximum is achieved on the boundary. So we will check the value of \(P_{t+1}\) for the point \(P_t\) at infinity and at its admissible minimum \({\tilde{P}}_t\). Now letting \(P_t\) goes to infinity, we have
and for \(P_t={\tilde{P}}_t\), we have
One can observe that \(P_{t+1}\) as a function of \(R_t\) has a similar behaviour. So for \(P_{t+1}\) to achieve its maximum, \(({\tilde{P}}_t, R_t)\) should be minimum and \((Q_{t+1},R_{t+1})\) should be maximum. So if we let \(Q_{\max }=\max \{{\bar{Q}}_1,{\bar{Q}}_2,\cdots , {\bar{Q}}_T\}\), \(Q_{\min }=\min \{{\bar{Q}}_1,{\bar{Q}}_2,\cdots , {\bar{Q}}_T\}\), \(R_{\max }=\max \{{\bar{R}}_1,{\bar{R}}_2,\cdots ,{\bar{R}}_T\}\), \(R_{\min }=\min \{{\bar{R}}_1,{\bar{R}}_2,\cdots ,{\bar{R}}_T\}\), and
we obtain that for all \(t>0\)
\(\square \)
We illustrate in the next remark as to why the argument that we have used above cannot be readily extended to non-scalar cases.
Remark A.2
The procedure that we have used above to prove boundedness of \( P_t \) relied on studying the evolutions of \( P_{t+1} \) as a function of \( P_t \). When these quantities are not scalars, one naturally aims to consider the norm of \( P_{t+1} \) as a function of the norm of \( P_t \). However, an example can be constructed where \(P_{t+1}\) as a function of \(P_t\) becomes unbounded as \(P_t\) approaches the boundary of the set positive-definite matrices that make \(K_{t+1}\) unstabilizing. This does not happen in the scalar case since this boundary is smaller than \({\tilde{P}}_t\), the minimum achievable \(P_t\). Figure 5 depicts the norm of \(P_{t+1}\) for different trials of selecting \(P_t\). For each trial, the \(P_t\) is chosen as \(P_t = P^* + \Omega \), where \(P^*\) is the minimum achievable \(P_t\) for a stabilizing matrix \(K_t\), and \(\Omega \) is a positive definite matrix. It can be seen that the norm of \(P_{t+1}\) for some trials gets very large. For example, for \(P_t\)
the matrix \(A-BK_{t+1}\) has the eigenvalues
and the first eigenvalue that is near 1, which makes the norm of \(P_{t+1}\) around the order of \(7.7\times 10^8\). However, in several simulations of online Riccati algorithm, we observed that changes in \(P_t\) as a result of changes in bounded \({\bar{Q}}_t\) and \({\bar{R}}\) do not make \(K_{t+1}\) to get close to the unstabilizing policy boundary, and hence \(P_{t+1}\) cannot get unbounded. We will show this behaviour in the following experiment.
Example A.3
In order to observe the behaviour of matrices \(P_t\) over time, a linear discrete-time control system with \(n=7\) states and \(m=5\) control actions is considered, where the matrices (A, B) are fixed.
We used several trials, where for each trial a sequence of positive definite random matrices \(Q_t\) and \(R_t\) with Wishart distribution is generated and we used the online Riccati algorithm with different initialization \(K_1\) to generate the sequence \(P_t\). Figure 6 shows the graph of the norm of \(P_t\) over time for each trial. Clearly, \(P_t\) stays bounded. Similar property is observed in all our simulation studies. Understanding why this boundedness occurs and if this is generally true is an important open problem, and appears to be difficult in light of the previous remark.
Rights and permissions
About this article
Cite this article
Akbari, M., Gharesifard, B. & Linder, T. Logarithmic regret in online linear quadratic control using Riccati updates. Math. Control Signals Syst. 34, 647–678 (2022). https://doi.org/10.1007/s00498-022-00323-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00498-022-00323-4