Static uncertain behavioral game with application to investment problem

Abstract

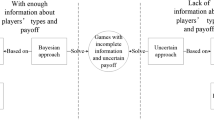
Uncertain game considers situations in which payoffs are characterized by uncertain variables. This paper goes further by taking into account players’ behaviors. For uncertain game with normal form, we define a new spectrum of uncertain behavioral game. Then, with the frame work of behavioral game theory and uncertainty theory, the expected Nash equilibrium is proposed. A necessary condition is provided in order to find the expected Nash equilibrium. Finally, an example is provided for illustrating purpose.

Appendix A

1.1 Uncertainty theory

Uncertain theory, founded by Liu (2007) and refined by Liu (2010), is a branch of axiomatic mathematics for modeling human uncertainty. Let $\varGamma$ be a non-empty set, ${\mathcal {L}}$ a $\sigma$-algebra over $\varGamma$, and each element $\varLambda$ in ${\mathcal {L}}$ is called an event. Uncertain measure is defined as a function from ${\mathcal {L}}$ to [0,1]. In detail, Liu (2007) gave the concept of uncertain measure as follows.

Definition A.1

(Liu 2007) The set function ${\mathcal {M}}$ is called an uncertain measure if it satisfies

Axiom 1. ${\mathcal {M}}\{\varGamma \}=1$ for the universal set $\varGamma$;

Axiom 2. ${\mathcal {M}}\{\varLambda \}+{\mathcal {M}}\{\varLambda ^c\}=1$ for any event $\varLambda$;

Axiom 3. For any countable sequence of events $\varLambda _1,\varLambda _2,$$\ldots ,$ we have

$$\begin{aligned} {\mathcal {M}}\left\{ \mathop {\bigcup }\limits _{i=1}^{\infty } \varLambda _i \right\} \le \sum \limits _{i=1}^{\infty } {\mathcal {M}}\left\{ \varLambda _i \right\} . \end{aligned}$$

(A.1)

Besides, in order to provide the operational law, Liu (2009) defined the product uncertain measure on the product $\sigma$-algebra ${\mathcal {L}}$ as follows.

Axiom 4. Let $(\varGamma _k,{\mathcal {L}}_k,{\mathcal {M}}_k)$ be uncertainty spaces for $k=1,2,\ldots$. The product uncertain measure ${\mathcal {M}}$ is an uncertain measure satisfying:

$$\begin{aligned} {\mathcal {M}}\left\{ \mathop {\prod }\limits _{k=1}^{\infty } \varLambda _k \right\} =\mathop {\bigwedge }\limits _{k=1}^{\infty } {\mathcal {M}}_k \left\{ \varLambda _k \right\} \end{aligned}$$

(A.2)

where $\varLambda _k$ are arbitrarily chosen events from ${\mathcal {L}}_k$ for $k=1,2 \ldots$, respectively. Based on the concept of uncertain measure, we can define an uncertain variable.

Definition A.2

(Liu 2007) An uncertain variable is a function $\xi$ from an uncertainty space $(\varGamma ,{\mathcal {L}},{\mathcal {M}})$ to the set of real numbers such that $\{\xi \in B\}$ is an event for any Borel set B of real numbers.

Definition A.3

(Liu 2007) The uncertainty distribution $\varPhi$ of an uncertain variable $\xi$ is defined by

$$\begin{aligned} \varPhi (x)={\mathcal {M}}\{ \xi \le x \} \end{aligned}$$

(A.3)

for any real number x.

Example A.1

An uncertain variable $\xi$ is called normal if it has a normal uncertainty distribution

$$\begin{aligned} \varPhi (x)=\left( 1+\text {exp}\left( \frac{\pi (e-x)}{\sqrt{3}\sigma }\right) \right) ^{-1}, \quad x \in \mathfrak {R}\end{aligned}$$

(A.4)

denoted by ${\mathcal {N}}(e,\sigma )$ where e and $\sigma$ are real numbers with $\sigma >0$.

Definition A.4

(Liu 2010) An uncertainty distribution $\varPhi (x)$ is said to be regular if it is a continuous strictly increasing function with respect to x at which $0<\varPhi (x)<1$, and

$$\begin{aligned} \lim \limits _{x \rightarrow {-\infty } } \varPhi (x) = 0, \quad \lim \limits _{x \rightarrow +{\infty } } \varPhi (x)=1. \end{aligned}$$

(A.5)

Definition A.5

(Liu 2010) Let $\xi$ be an uncertain variable with regular uncertainty distribution $\varPhi (x)$. Then the inverse function $\varPhi ^{-1}(\alpha )$ is called the inverse uncertainty distribution of $\xi$.

Example A.2

The inverse uncertainty distribution of normal uncertain variable ${\mathcal {N}}(e,\sigma )$ is

$$\begin{aligned} \varPhi ^{-1}(\alpha ) = e + \frac{\sigma \sqrt{3}}{\pi } \text {ln} \frac{\alpha }{1-\alpha }. \end{aligned}$$

(A.6)

Definition A.6

(Liu 2009) The uncertain variable $\xi _1, \xi _2, \ldots , \xi _n$ are said to be independent if

$$\begin{aligned} {\mathcal {M}}\left\{ \mathop {\bigcap }\limits _{k=1}^{n} (\xi _i \in B_i) \right\} = \mathop {\bigwedge }\limits _{k=1}^{n} {\mathcal {M}}\left\{ \xi _i \in B_i \right\} \end{aligned}$$

for any Borel sets $B_1, B_2, \ldots , B_n$ of real numbers.

Definition A.7

(Liu 2007) Let $\xi$ be an uncertain variable. The expected value of $\xi$ is defined by

$$\begin{aligned} \text {E}[\xi ]={\int }_0^{+ \infty } {\mathcal {M}}\{\xi \ge r \}\text {d}x-{\int }_{-\infty }^{0}{\mathcal {M}}\{\xi \le r \}\text {d}x \end{aligned}$$

(A.7)

provided that at least one of the above two integrals is finite.

Based on the definition of inverse uncertainty distribution, we can get the theorem below, which is convenient to calculate the expected value of uncertain variable.

Theorem A.1

(Liu 2007) Let $\xi$ be an uncertain variable with regular uncertainty distribution $\varPhi$. If the expected value exists, then

$$\begin{aligned} \text {E}[\xi ]={\int }_0^1 \varPhi ^{-1}(\alpha ) \mathrm{d} \alpha . \end{aligned}$$

(A.8)