Joint design and compression of convolutional neural networks as a Bi-level optimization problem

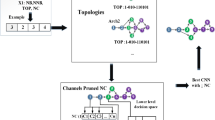
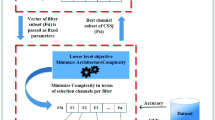
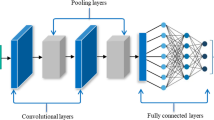
Abstract

Over the last decade, deep neural networks have shown great success in the fields of machine learning and computer vision. Currently, the CNN (convolutional neural network) is one of the most successful networks, having been applied in a wide variety of application domains, including pattern recognition, medical diagnosis and signal processing. Despite CNNs’ impressive performance, their architectural design remains a significant challenge for researchers and practitioners. The problem of selecting hyperparameters is extremely important for these networks. The reason for this is that the search space grows exponentially in size as the number of layers increases. In fact, all existing classical and evolutionary pruning methods take as input an already pre-trained or designed architecture. None of them take pruning into account during the design process. However, to evaluate the quality and possible compactness of any generated architecture, filter pruning should be applied before the communication with the data set to compute the classification error. For instance, a medium-quality architecture in terms of classification could become a very light and accurate architecture after pruning, and vice versa. Many cases are possible, and the number of possibilities is huge. This motivated us to frame the whole process as a bi-level optimization problem where: (1) architecture generation is done at the upper level (with minimum NB and NNB) while (2) its filter pruning optimization is done at the lower level. Motivated by evolutionary algorithms’ (EAs) success in bi-level optimization, we use the newly suggested co-evolutionary migration-based algorithm (CEMBA) as a search engine in this research to address our bi-level architectural optimization problem. The performance of our suggested technique, called Bi-CNN-D-C (Bi-level convolution neural network design and compression), is evaluated using the widely used benchmark data sets for image classification, called CIFAR-10, CIFAR-100 and ImageNet. Our proposed approach is validated by means of a set of comparative experiments with respect to relevant state-of-the-art architectures.

Appendices

Appendix A Manually designed CNN architectures used for compression

The most evocative examples of manual architecture are VGG16, VGG19, ResNet50, DenseNet50 and ResNet110. The details of the CNN architectures used to compare the proposed approach are summarized in Table 10.

Table 10 CNN architectures overview for comparing the suggested approach

Appendix B Bi-level optimization’s main definitions

In the academic and real-world optimization problems, the majority uses a single level of optimization. Multiples problems, however, are designed as two levels, referred to as BLOP [75]. We uncover a problem of optimization nested within external optimization constraints in such scenarios. The upper-level problem, often known as the leader problem, is considered as an external task of optimization. The nested internal optimization work called also a follower problem or a lower level, and the two-level problem is referred to as a leader–follower problem or a Stackelberg game [76]. The follower problem looks like a constraint at the upper level; therefore, uniquely the best solution with regard to the follower optimization problem could be considered as a leader candidate.

Definition: Assuming $\Re ^{n}\times \Re ^{n} \rightarrow \Re$ to be the leader problem and $f:\Re ^{n}\times \Re ^{n} \rightarrow \Re$ to be the follower one, analytically, a BLOP could be stated as follows:

$$\begin{aligned}&\mathrm{Min}{_{x_{u} \in X_{U},x_{l}\in X_{L}}}L(x_{u},x_{l}) \nonumber \\&\mathrm{subject} \, to \left\{ \begin{matrix} x_{l}\in \mathrm{ArgMin} \begin{Bmatrix} f(x_{u},x_{l}),g_{j}(x_{u},x_{l}))\le 0,j=1,\ldots ,J \end{Bmatrix}\\ G_{k}(x_{u},x_{l})\le 0,k=1,\ldots ,K . \end{matrix}\right. \end{aligned}$$

(B1)

There are two types of variables in a BLOP: variables of the upper-level variables and variables of the lower level. The optimization work for the follower problem is done against the $x_{l}$ variables, with the $x_{u}$ variables acting as fixed parameters. As a result, each $x_{u}$ represents a new follower issue, the optimal solution of which is a function of $x_{u}$ and must be found. In the leader problem, all variables ($x_{u}$, $x_{l}$) are examined, with the exception of $x_{l}$. The formal definition of BLOP is provided below:

Single-level problems are intrinsically more complex to solve than BLOPs. It is not unexpected that the majority of previous research has focused on the more straightforward situations of BLOP, such as problems with good features like linear objectives, constraint functions, convexity or quadraticity [77]. Despite the fact that it was the first study on bi-level optimization originates from the 1970s, the utility of these mathematical programs in representing hierarchical decision-making engineering and processes challenges were not realized until the early 1980s. BLOPs have encouraged researchers to devote special attention to them. Kolstad [75] compiled the first bibliographic survey on the subject (1985) in the mid-1980s.

Fig. 10

An example of a single-objective BLOP with two levels is illustrated [1]

Existing BLOP-solving methods can be divided into two groups: (1) classical methods while (2) evolutionary methods. Number one family preserves extreme point-based approaches such as [78], branch-and-bound [79], penalty function methods [80], complementary pivoting [81] and methods of trust region [82]. These strategies have a disadvantage which is that they are significantly reliant to the mathematical properties of the BLOP in question. Metaheuristic algorithms, which are mostly evolutionary algorithms, belong to the second family (EA). Several EAs have recently proved their efficacy in addressing such problems due to their insensitivity to the mathematical properties of the problem, as well as their capacity to handle enormous problem instances by offering satisfactory answers in a fair amount of time. Here are a few examples of notable works [80, 81].

Appendix C Main principle of CEMBA

As for each upper-level architecture there exists a whole search space of possible filter pruning decisions, the joint neural architecture search and (filter) compression are framed as a bi-level optimization problem. Motivated by the recent emergence of the field of EBO (evolutionary bi-level optimization) and the related achieved interesting results in many application fields, we decided to use the evolutionary algorithm as a search engine to solve our bi-level optimization problem. The main difficulty faced in EBO is the important computational cost it needs. This is because each the fitness evaluation of each upper-level solution requires running a whole lower-level evolutionary process to approximate the optimal corresponding lower-level solution. Through the literature there exist many EBO algorithms [83], but most of them focus on problems with continuous variables (using approximation techniques and gradient information). The number of algorithms that were designed for the discrete case is much reduced with regard to the continuous case. Examples of discrete EBO algorithms are NBEA, BLMA, CODBA, CODCRO and CEMBA [84]. As the majority of algorithms deal with the continuous situation, CEMBA among the most effective bi-level EAs for dealing with discrete scenarios that has been demonstrated [17]. Every upper-level solution is evaluated using 2 stages: first, the variables of the upper-level are directed to the lower level; and second, the indicator-based multi-objective local search gets closer to the solution with the maximum marginal contribution in terms of multi-objective quality indicator and sends it to the next level to complete the evaluation of the quality of the consideration. To summarize how it works, we will go over the research processes of its upper and lower levels:

• Upper and lower population initialization Create the upper-level population and the lower-level population from scratch. Two starting populations were obtained by using the Discrete Space Decomposition Method twice. The goal of utilizing a decomposition approach is to produce uniform coverage of the decision space and, to the extent possible, a collection of solutions that are evenly dispersed over every level decision space.

• Lower-level fitness assignment To assess an upper-level solution in BLOP, a bi-level optimization problem necessitates to execute of an entire lower-level method, which is the BLOP’s fundamental challenge. As a result, we dissect each problem level using 2 populations for solving it. The lower-level algorithm of each lower population employs the higher solutions of the matching upper population to evaluate the lower-level solutions.

• Local search procedure The local search is applied for each lower-level population using the IBMOLS principle for the lower-level method. In fact, we begin by calculating the objective function’s normalized values. As a result, for each lower solution, we create a neighborhood and then calculate its fitness value using an indicator I and the objective function’s normalized values. An update of the fitness values is then performed, the worst-case solution is removed, and the fitness values are updated again. It is worth noting that neighborhood generation comes to a halt in one of two situations: (1) whenever entire solution neighborhood has been examined, or (2) in case an adjacent solution that improves (with regard to I) is discovered. In case that all lower-level members have been visited, the entire local search procedure comes to an end.

• Best indicator contribution lower-level solution determination Because evaluating the upper-level population’s leader solutions necessitates approximating each matching lower-level population’s follower solution, the lower-level solutions are compared to the members of the upper-level.

• Upper-level indicator-based procedure Each higher-level population performs its algorithm based on the IBEA after obtaining the lower-level solutions with the best indicator contribution of the follower problem. This is because we find the person with the lowest fitness value, delete him or her and then update the fitness values of the remaining people until we reach the stop criterion. After that, mating selection and variation are used. We should remark that using IBEA aids the algorithm in approximating the best upper front.

• Migration strategy (each $\alpha$ generations) After a certain number of generations, use a migration strategy. As a result, we use the parameter $\beta$ to select a set of solutions that includes $\beta$ objective follower space solutions. The migration step employs this pre-selected collection of solutions.

Appendix D Tuning of parameters

The Taguchi method [85] is a sophisticated case of the trial-and-error one [86]. In order to clarify more and verify the proposed parameter tuning values, we have applied the Taguchi method in which the signal-to-noise ratio (SNR) parameter is calculated as follows:

$$\begin{aligned} \hbox {SNR}=-log_{10}\left(\frac{1}{N}\sum _{i=1}^{N}\hbox {(objective function)}_{i}^{2}\right) \end{aligned}$$

(D2)

Fig. 11

Signal to noise

Fig. 12

Mean of means

where N represents the number of performed runs. The SNR parameter reflects the variability and the mean of the experimental data. The used parameters for tuning are the following: (1) population size (Pop. size), (2) upper generation number (UGen. nb) and (3) lower generation number (LGen. nb). The considered levels for each parameter, while the corresponding orthogonal array (L27(33 ) where we have 27 experiments, 3 variables and 2 levels. Figure 11 displays the obtained SNR results for IB-CEMBA. Moreover, Fig. 12 displays computed results for Bi-CNN-D-C in terms of mean fitness values of the upper-level in Taguchi experimental analysis, which confirmed the achieved optimal levels using SNR parameter. In fact, the computed mean upper-level fitness values confirmed the achieved optimal level using SNR parameter.