Abstract
The efficient treatment of dense matrices arising, e.g., from the finite element discretisation of integral operators requires special compression techniques. In this article, we use a hierarchical low-rank approximation, the so-called 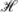 -matrix, that approximates the dense stiffness matrix in admissible blocks (corresponding to subdomains where the underlying kernel function is smooth) by low rank matrices. The low rank matrices are assembled by the ACA+ algorithm, an improved variant of the well-known ACA method. We present an algorithm that can determine a coarser block structure that minimises the storage requirements (enhanced compression) and speeds up the arithmetic (e.g., inversion) in the
-matrix, that approximates the dense stiffness matrix in admissible blocks (corresponding to subdomains where the underlying kernel function is smooth) by low rank matrices. The low rank matrices are assembled by the ACA+ algorithm, an improved variant of the well-known ACA method. We present an algorithm that can determine a coarser block structure that minimises the storage requirements (enhanced compression) and speeds up the arithmetic (e.g., inversion) in the 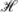 -matrix format. This coarse approximation is done adaptively and on-the-fly to a given accuracy such that the matrix is assembled with minimal storage requirements while keeping the desired approximation quality. The benefits of this new recompression technique are demonstrated by numerical examples.
-matrix format. This coarse approximation is done adaptively and on-the-fly to a given accuracy such that the matrix is assembled with minimal storage requirements while keeping the desired approximation quality. The benefits of this new recompression technique are demonstrated by numerical examples.
Similar content being viewed by others
References
Bebendorf, M.: Approximation of boundary element matrices. Numer. Math. 86(4), 565–589 (2000).
Bebendorf, M.: Hierarchical LU decomposition based preconditioners for BEM. Technical Report 28, Max-Planck-Institute for Mathematics in the Sciences 2004.
Bebendorf, M., Rjasanov, S.: Adaptive low-rank approximation of collocation matrices. Computing 70, 1–24 (2003).
Börm, S., Grasedyck, L.: HLib – a library for
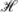 - and
- and 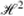 -matrices, 1999. Available at http://www.hlib.org.
-matrices, 1999. Available at http://www.hlib.org.Börm, S., Grasedyck, L.: Low-rank approximation of integral operators by interpolation. Computing 72, 325–332 (2004).
Börm, S., Grasedyck, L., Hackbusch, W.: Introduction to hierarchical matrices with applications. Engineering Analysis with Boundary Elements 27, 405–422 (2003).
Dahmen, W., Schneider, R.: Wavelets on manifolds I: Construction and domain decomposition. SIAM J. Math Anal. 31, 184–230 (1999).
Sauter, S. A., Erichsen, S.: Efficient automatic quadrature in 3-D Galerkin BEM. Comput. Meth. Appl. Mech. Eng. 157, 215–224 (1998).
Grasedyck, L.: Theorie und Anwendungen Hierarchischer Matrizen. PhD thesis, Universität Kiel 2001.
Grasedyck, L., Hackbusch, W.: Construction and arithmetics of
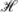 -matrices. Computing 70, 295–334 (2003).
-matrices. Computing 70, 295–334 (2003).Greengard, L., Rokhlin, V.: A new version of the fast multipole method for the Laplace in three dimensions. In: Acta Numerica 1997, pp. 229–269. Cambridge University Press 1997.
Hackbusch, W.: A sparse matrix arithmetic based on
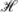 -matrices. Part I: Introduction to
-matrices. Part I: Introduction to 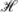 -matrices. Computing, 62, 89–108 (1999).
-matrices. Computing, 62, 89–108 (1999).Hackbusch, W., Khoromskij, B.: A sparse matrix arithmetic based on
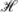 -matrices. Part II: Application to multi-dimensional problems. Computing 64, 21–47 (2000).
-matrices. Part II: Application to multi-dimensional problems. Computing 64, 21–47 (2000).Hackbusch, W., Khoromskij, B., Kriemann, R.: Hierarchical matrices based on a weak admissibility criterion. Technical Report 2, Max-Planck Institute for Mathematics in the Sciences, 2003. Computing 73, 207–243 (2004).
Hackbusch, W., Nowak, Z. P.: On the fast matrix multiplication in the boundary element method by panel clustering. Numer. Math. 54, 463–491 (1989).
Lintner, M.: The eigenvalue problem for the 2d Laplacian in
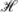 -matrix arithmetic and application to the heat and wave equation. Computing 72, 293–323 (2004).
-matrix arithmetic and application to the heat and wave equation. Computing 72, 293–323 (2004).Rokhlin, V.: Rapid solution of integral equations of classical potential theory. J. Comput. Phys. 60, 187–207 (1985).
Saad, Y., Schultz, M.: GMRES: a generalized minimal residual algorithm for solving nonsymmetric linear systems. SIAM J. Sci. Statist. Comput. 7, 856–869 (1986).
Sauter, S. A.: Variable order panel clustering (extended version). Technical Report 52, Max-Planck-Institute for Mathematik, Leipzig, Germany, 1999.
Tyrtyshnikov, E.: Incomplete cross approximation in the mosaic-skeleton method. Computing 64, 367–380 (2000).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Grasedyck, L. Adaptive Recompression of  -Matrices for BEM.
Computing 74, 205–223 (2005). https://doi.org/10.1007/s00607-004-0103-1
-Matrices for BEM.
Computing 74, 205–223 (2005). https://doi.org/10.1007/s00607-004-0103-1
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00607-004-0103-1





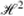 -matrices, 1999. Available at
-matrices, 1999. Available at