Skip to main content

Advertisement

Springer Nature Link
Log in

Catastrophic chaos theory: predicting recovery of health or death

  • Original Article
  • Published:
Artificial Life and Robotics Aims and scope Submit manuscript

Abstract

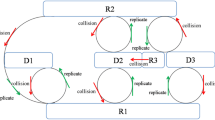
Recently, we revealed a standard pattern of a macroscopic molecular network for controlling morphogenetic processes such as the development of organs, including blast, mesoderm, heart, and hands during about sevenfold cell divisions and a standard bio-chemical clock like the circadian one (Naitoh in Artif Life Robot 13, 2008; Japan J Ind Appl Math 28(1), 2011; J Phys Conf Ser 344, 2012; Artif Life Robot 17, 2012) A network model derived logically based on experimental observations is described by a nonlinear differential equation for predicting time evolutions of six macroscopic molecular groups: three gene groups and three enzyme groups, which include promoting and suppressing factors. Here, the macroscopic model extended for also describing aging processes shows various types of cycles and reveals the physical condition for determining whether or not living beings such as humans can survive after getting ill. It is stressed that, after becoming ill, living systems with overly fast generation of information molecules such as various genes end in death, whereas relatively fast production of enzymes leads to recovery. This may also explain an essential feature underlying carcinogenic processes.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+
from $39.99 /Month
  • Starting from 10 chapters or articles per month
  • Access and download chapters and articles from more than 300k books and 2,500 journals
  • Cancel anytime
View plans

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

Explore related subjects

Discover the latest articles and news from researchers in related subjects, suggested using machine learning.

References

  1. Lowe TM, Eddy SR (1997) Nucleic Acids Res 25:955. http://rna.wustl.edu/tRNAdb/)

    Google Scholar 

  2. Nakamura Y, Gojobori T, Ikemura T (2000) Nucl Acids Res 28:292. http://www.kazusa.or.jp/codon/)

    Google Scholar 

  3. DNA Data Bank of Japan. http://www.ddbj.nig.ac.jp/

  4. Ashburner M et al (2000) Gene Ontology: tool for the unification of biology. Nat Genet 25:25–29

    Article  Google Scholar 

  5. Purcell O et al (2010) A comparative analysis of synthetic genetic oscillators. J R Soc Interface 7:1503–1524

    Article  Google Scholar 

  6. Hase T, Tanaka H, Suzuki Y, Nakagawa S, Kitano H (2009) Structure of protein interaction networks and their implications on drug design. PLoS Comput Biol 5(10)

  7. Reilly PR (2004) Is it in your genes?. Cold Spring Harbor Laboratory Press, New York, pp 1–288

    Google Scholar 

  8. Shimizu N (2004) Genome wo kiwameru. Kodansha Scientific, Tokyo, pp 1–144

    Google Scholar 

  9. Naitoh K, Shimiya H (2011) Stochastic determinism. Japan J Ind Appl Math 28–1:3–14

    Google Scholar 

  10. Waddington CH (1957) The strategy of the genes. George Allen & Unwin, London, pp 1–262

    Google Scholar 

  11. Kaufman S (1993) The origin of order. Oxford Press, Oxford, pp 1–717

    Google Scholar 

  12. Eigen M (1992) Steps toward life. Oxford University Press, Oxford, pp 1–173

    Google Scholar 

  13. Prusinkiewiez P, Lindenmayer A (1990) The algorithm of beauty of pants. Springer, Berlin, pp 1–228

    Google Scholar 

  14. Naitoh K (1998) Macroscopic kinetic equation for genetic algorithm. Japan J Ind Appl Math 15–1:87–133

    Article  MathSciNet  Google Scholar 

  15. Naitoh K (1998) Introns for accelerating quasi-macroevolutions. JSME Int J C 41–3:398–405

    Article  Google Scholar 

  16. Mullis KB (1990) The unusual origins of the polymerase chain reactions. Sci Am 262:56–65

    Article  Google Scholar 

  17. Naitoh K (2008) Stochastic determinism. Artif Life Robot 13: 10–17. (also in Naitoh K (2008) Onto-biology: inevitability of five bases and twenty amino-acids. Proceedings of 13th international conference on biomedical engineering (ICBME), Singapore. Springer, Berlin)

  18. Naitoh K (2011) Morphogenic economics. Japan J Ind Appl Math 28(1):15–26

    Google Scholar 

  19. Naitoh K (1999) Cyto-fluid dynamic theory. Oil Gas Sci Technol 54:205–210

    Google Scholar 

  20. Naitoh K (2001) Cyto-fluid dynamic theory. Japan J Ind Appl Math 18(1):75–105

    Google Scholar 

  21. Naitoh K (2011) Onto-neurology. In: Proceedings of JSST2011 international conference on modeling and simulation technology, Tokyo, pp 322–327

  22. Naitoh K (2011) Quasi-stability. In: Proceedings of 15th Nordic and Baltic conference on biomedical engineering and biophysics, Denmark

  23. Naitoh K (2012) Spatiotemporal structure: common to subatomic systems, biological processes, and economic cycles. J Phys Conf Ser 344:1–18

    Google Scholar 

  24. Naitoh K (2012) Hyper-gourd theory. Artif Life Robot 17:275–286

    Google Scholar 

  25. Naitoh K (2010) Onto-biology. Artif Life Robot 15:117–127

  26. Naitoh K (2011) Onto-oncology: a mathematical physics underlying the proliferation, differentiation, apoptosis, and homeostasis in normal and abnormal morphogenesis and neural system. Proceedings of 15th Nordic and Baltic conference on biomedical engineering and biophysics, IFMBE proceedings 34, Denmark, pp 29–32

  27. Naitoh K (2009) Onto-biology: clarifying also the standard clock for pre-biotic process, stem-cell, organs, brain, and societies. In: Proceedings of CBEE, Singapore

  28. Naitoh K (2011) The universal bio-circuit: underlying normal and abnormal reaction networks including cancer. In: Proceedings of European IFMBE conference, IFMBE proceedings, Budapest, vol 37, pp 247–250

  29. Takahashi K, Yamanaka S (2006) Induction of pluripotent stem cells from mouse embryonic and adult fibroblast cultures defined factors. Cell 126:663–676

    Google Scholar 

  30. Gilbert SF (2006) Developmental biology, 8th edn. Sinauer Associates, Sunderland, pp 211–251

    Google Scholar 

  31. Nishikawa S (ed) (2008) Ultimate stem cell. Newton 6, pp 12–55

  32. Bear MF, Connors BW, Paradiso MA (2007) Neuroscience. Lippincott Williams & Wiklins Inc., USA, pp 1–855

    Google Scholar 

  33. Hodgkin AL, Huxley AF (1952) A quantitative description of membrane current and its application to conduction and excitation in nerve. J Physiol 117:500–544

    Google Scholar 

  34. Naitoh K (2013) Catastrophic chaos theory: predicting the edge between health and death. In: Proceedings of 18th international symposium on artificial life and robotics

  35. Edelman G (2004) Wider than the sky. Yale University Press, London, pp 1–224

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Waseda University, 3-4-1 Ookubo, Shinjuku, Tokyo, 169-8555, Japan

    Ken Naitoh & Hirofumi Inoue

Authors
  1. Ken Naitoh
    View author publications

    Search author on:PubMed Google Scholar

  2. Hirofumi Inoue
    View author publications

    Search author on:PubMed Google Scholar

Corresponding author

Correspondence to Ken Naitoh.

About this article

Cite this article

Naitoh, K., Inoue, H. Catastrophic chaos theory: predicting recovery of health or death. Artif Life Robotics 18, 127–132 (2013). https://doi.org/10.1007/s10015-013-0109-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10015-013-0109-x

Keywords