A multi-scale template method for shape detection with bio-medical applications

Abstract

In this paper we present a novel methodology based on non-parametric deformable prototype templates for reconstructing the outline of a shape from a degraded image. Our method is versatile and fast and has the potential to provide an automatic procedure for classifying pathologies. We test our approach on synthetic and real data from a variety of medical and biological applications. In these studies it is important to reconstruct accurately the shape of the object under investigation from very noisy data. Here we assume that we have some prior knowledge about the object outline represented by a prototype shape. Our procedure deforms this shape by means of non-affine transformations and the contour is reconstructed by minimizing a newly developed objective function that depends on the transformation parameters. We introduce an iterative template deformation procedure in which the scale of the deformation decreases as the algorithm proceeds. We compare our results with those from a Gaussian Mixture Model segmentation and two state-of-the-art Level Set methods. This comparison shows that the proposed procedure performs consistently well on both real and simulated data. As a by-product we develop a new filter that recovers the connectivity of a shape.

Appendix

1.1 A1. Range of deformation parameters

For a detailed derivation of the deformation model, see [33]. Here we start from:

$${{\mathbf{U}}}_{{{\varvec{\Uptheta}}}}\left(x,y\right)=\frac{1}{2 \alpha \pi^{2}} {{\mathbf{\varepsilon}}}\otimes {{\mathbf{\psi}}}(x,y), $$

(7)

in which ${\varvec{\varepsilon}}=\left[\varepsilon^{1},\varepsilon^{2}\right],\; {\varvec{\psi}}=\left[2 \sin \left( \pi x \right) \cos \left( \pi y \right),2 \cos \left( \pi x \right) \sin \left( \pi y \right) \right]$ and ${\varvec{ \Uptheta}}=(\alpha;{\varvec{\varepsilon}}).$ In order to widen the class of deformations that we consider, we shall assume that ɛ ¹ _nm and ɛ ² _nm can take any value in [−1, 1] independently of each other.

We now discuss suitable ranges for the deformation parameters. Since we want every point of S to be mapped within the unit square, the minimum value of α can be obtained by requiring that the maximum deformation in both directions will never leave the unit square. We discuss this for the x direction; an analogous treatment applies for the y direction. First of all, we consider a point (x, y) very close to the border (0, y). We require that this point will be mapped within S, so that applying the maximum negative deformation in the x direction must yield a non-negative transformed point. The maximum negative deformation corresponding to ɛ¹ = −1 must satisfy:

$$x-\frac{1}{\alpha \pi^{2}} \sin\left(\pi x\right) \cos\left(\pi y \right) \geq 0. $$

(8)

Since x is small we approximate sin(πx) by πx, and in order to have the biggest deformation we set cos(πy) = 1. With these simplifications (8) becomes:

$$x-\frac{x}{\alpha \pi}=x\left(1-\frac{1}{\alpha \pi} \right) \geq 0 $$

from which it follows that

$$ \alpha \geq \frac{1}{\pi} \sim 0.32.$$

Analogously, if we take a point close to the border (1, y) we require that the biggest positive deformation corresponding to ɛ¹ = 1 will not map this point beyond the border so that:

$$x+\frac{1}{\alpha \pi^{2}} \sin\left(\pi x\right) \cos\left(\pi y \right)\leq 1. $$

(9)

Now, since x is very close to 1, we can approximate sin(π x) by π(1 − x) and as before in order to have the biggest deformation we take cos(πy) = 1. Hence, (9) becomes:

$$x+\frac{\pi\left(1-x \right)}{\alpha \pi^{2}} \leq 1, $$

leading again to the same constraint

$$ \alpha \geq \frac{1}{\pi} \sim 0.32.$$

Now, because of the discretization of the mapping we will assume the value 0.4 for the minimum of α. The maximum value of α can be obtained by requiring that the maximum deformation is greater than the distance between two adjacent pixels. This happens when

$$ \frac{1}{\alpha \pi^{2}} > \frac{1} {50}$$

because the pixel grids that we use are typically of size 50 × 50. In this way, if

$$\alpha < \frac{50}{\pi^{2}} \sim 5$$

every point of S will be mapped into itself and no effect of the deformation will be visible. In conclusion, we adopted the range [0.4, 5] for the scale parameter α.

1.2 A2. The power of the test

We choose w by considering the power of the test:

$$ {\it P}\left({{\it H}_{0}\; \hbox{is rejected}} \vert {{\it H}_{1}\; \hbox{is true}} \right) = {\it P}\left( W \geq w \vert W \sim {\it N}\left(\frac{\mu_{\texttt{I}}-\mu_{\texttt{E}}} {\sqrt{\sigma^{2}_{{\texttt{I}}}+\sigma^{2}_{{\texttt{E}}}}},1\right)\right). $$

In particular, let us require power λ when

$$ {\frac{\mu_{\texttt{I}}-\mu_{\texttt{E}}}{\sqrt{\sigma^{2}_{{\texttt{I}}}+\sigma^{2}_{{\texttt{E}}}}}}=\delta > 0.$$

That is, we require P(W ≥ w | W ∼ N(δ, 1)) = λ. Hence, P(W − δ ≥ w − δ| W − δ ∼ N(0, 1)) = λ, so that 1 − Φ(w − δ) = λ, or w = δ + Φ⁻¹(1 − λ), where Φ is the cumulative distribution function of a standard normal variable.

An upper bound on the probability of Type I error can be found as follows:

$$ \begin{aligned}{\it P}\left({{\it H}_{0}\; \hbox{is rejected}}| {{\it H}_{0}\; \hbox{is true}} \right)&=1-{\frac{1}{2}}\left\{\Phi\left({\frac{w} {\sqrt{2}}}\sqrt{1+{\frac{\sigma^{2}_{{\texttt{E}}}} {\sigma^{2}_{{\texttt{I}}}}}}\right)\right. \\ &\quad+\left. \Phi\left({\frac{w}{\sqrt{2}}}\sqrt{1+{\frac{\sigma^{2}_{{\texttt{I}}}}{\sigma^{2}_{{\texttt{E}}}}}}\right) \right\}, \end{aligned} $$

assuming that under H ₀ the probability that both pixels belong to I (or E ) is ${\frac{1}{2}}.$ Elementary calculus leads us to the bound:

$${\it P}\left({{\it H}_{0}\; \hbox{is rejected}}| {{\it H}_{0}\; \hbox{is true}} \right) \leq 1-\Phi(w), $$

with equality holding when $\sigma_{\texttt{I}}=\sigma_{\texttt{E}}.$ Hence, an upper bound for the probability of Type I error is 1 − Φ{δ + Φ⁻¹(1 − λ ) }. In our simulation study a conservative value of δ is 1.5. Thus, for power λ = 0.7, we can set w = 1. This choice leads to an upper bound for the probability of Type I error of 0.16, which is acceptable.

1.3 A3. A new filter to recover the connectivity

Although the operator ${{\mathcal{K}}}$ in (1) preserves the connectivity of the template on a continuous space, it may not always do so on a discrete space such as the space of image pixels. Because of the definition of the objective function given in Sect. 2.3, to perform our analysis we need a simply connected shape. In our model (2) the range of ${\varvec{\Uptheta}}$ has been set in such a way that connectivity is lost for only a few extreme deformations. When this happens the connectivity may be recovered by means of standard morphological operations such as the Bridge and Skeletonisation [35]. However, these standard morphological operators have the tendency to smooth the original shape as the following example illustrates. Figure 9a shows a single deformation of T ₀ corresponding to ${\varvec{\Uptheta}}=\left(0.4;1,-1\right).$ This represents one of the most extreme transformations that can be obtained by a single deformation. In order to recover a simply connected shape, first we apply a morphological Bridge transformation; see Fig. 9b. Although the shape is now connected, it is not simply connected since, the Bridge filter connects the borders every time the distance between them is less than two pixels so making narrow shapes multiply connected. One way to restore simple connectivity is to fill the internal holes and then to apply the morphological Skeletonisation; see Fig. 9c. This shape is now simply connected but it is much smoother than the original one in Fig. 9a with the result that some detailed information about the border has been lost. In order to obtain a more satisfactory connected shape than above we developed a new filter. Our new filter can be described as follows:

• 1. Following a fixed sweeping scheme, all the image pixels are visited until a shape pixel is found. This pixel becomes the current pixel and forms the first pixel of the filtered shape.

• 2. The second order neighbours of the current pixel are considered following a particular visiting scheme. The first shape pixel that has not yet been visited is selected. The current pixel becomes the old pixel and the selected pixel becomes the current pixel. The current pixel is added to the pixel of the filtered shape. The visiting scheme depends on the curvature of the shape at the current pixel and this is estimated by the relative location of the current and old pixel. Some visiting schemes are reported in Fig. 10. For the starting pixel of Step 1 a fixed visiting scheme is assumed.

• 3. Step 2 is repeated until the current pixel is a neighbour of the starting pixel. This always happens since the shape obtained by applying the Bridge filter is connected and the direction (in our case anticlockwise) is maintained throughout the algorithm.

Fig. 9

a An unconnected shape obtained by applying an extreme transformation to T ₀. b The output of the morphological Bridge filter. c The output of the morphological Hole Filling followed by Skeletonisation filter. d The result of applying the new Ext filter

Fig. 10

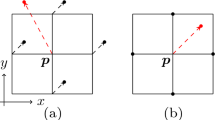
Visiting scheme for neighbouring pixels. The visiting order depends on the local curvature, estimated by the relative position of the current pixel ( cur ) and the old pixel ( old ). Three examples are shown. The first visiting scheme is the one adopted for the starting pixel, except in that case old would be replaced by 8

We call our new filter as the Ext filter. The result of this filter will always be the same when it is applied after the Bridge filter, provided that the starting shape pixel is one of the pixels of the outer border. In Fig. 9d we show the shape recovered by this filter. We note that our Ext filter has preserved the features of the border of the original shape shown in Fig. 9a much better than the previous approach shown in Fig. 9c. The Ext filter is also as fast as the morphology based approach (typically 1.6 × 10⁻² s per reconstruction), and is implemented in one step instead of two.