Sandwich games

Abstract

The extension of set functions (or capacities) in a concave fashion, namely a concavification, is an important issue in decision theory and combinatorics. It turns out that some set-functions cannot be properly extended if the domain is restricted to be bounded. This paper examines the structure of those capacities that can be extended over a bounded domain in a concave manner. We present a property termed the sandwich property that is necessary and sufficient for a capacity to be concavifiable over a bounded domain. We show that when a capacity is interpreted as the product of any sub group of workers per a unit of time, the sandwich property provides a linkage between optimality of time allocations and efficiency.

Appendix

Proof of Lemma 1

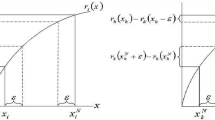
Fix a capacity $v$. The homogeneity of $e_v$ is implied by the definition of $\int ^{cav} \cdot dv$. Now, fix $x\in Q$ and consider a decomposition of $x$, $\sum _{S\subseteq N}\alpha _S \mathbf{1}_S=x$. Letting $i^*= \arg \max _{i\in \{1,\ldots ,n\}}$ $x_i$, we get that $\sum _{S\subseteq N}\alpha _S\ge \sum _{S\subseteq N, i^*\in S} \alpha _S=x_{i^*}=\max x$. Since $e_v(x)$ is the minimum over all such decomposition, we obtain $e_v(x)\ge \max x$. $\square$

Proof of Lemma 2

Let $v$ be a capacity defined over $N$ and $v_S$ its sub-capacity. If $v_S$ does not have the sandwich property, then there is an affine function $f_S(x)=a+\sum _{i\in S}a_ix_i$ (where $x\in [0,1]^S$) that dominates $v_S$, and there is no linear function dominated by $f_S$ and that is dominating $v_S$. Denote,

$$\begin{aligned} b={\mathop {\mathop {\max }_{A\subseteq S}}_{B\subseteq N\setminus S}} [v(A\cup B)-v(A)]. \end{aligned}$$

$b$ is the maximal contribution of a coalition $B$ in $N{\setminus }S$ to a coalition $A$ in $S$. Define the following affine function over $Q$, $f(x)=a+\sum _{i\in S}a_ix_i+ \sum _{i\in N\setminus S}bx_i$. It is clear that $f$ dominates $v$. Suppose, to the contrary of the assumption that $v$ does have the sandwich property and that there exists a linear function $\ell (x)=\sum _{i\in N}c_ix_i$, dominated by $f$ and is dominating $v$. Then, $\ell _S(x) =\sum _{i\in S}c_ix_i$ is dominated by $f_S$ and is dominating $v_S$. This is a contradiction.

On the other hand, if $v$ has the sandwich property, let $f_S$ be an affine function that dominates $v_S$. Define $f$ in the same way as defined above. By assumption, there is a linear function $\ell$ that is dominating $v$ and is dominated by $f$. The restriction of $\ell$ to $S$, $\ell _S$, is dominating $v_S$ and is dominated by $f_S$, implying that $v_S$ has the sandwich property. $\square$

Proof of Claim 1

Suppose that the core of $v$ is non-empty and let $\sum \alpha _S\mathbf{1}_S$ be a decomposition of $\mathbf{1}_N$, then by the Shapley-Bondareva theorem (Bondareva [4] and Shapley [14]), $\sum \alpha _Sv(S)\le v(N).$ Thus, the decomposition $\mathbf{1}_N$ of itself is optimal, implying that $e_v(\mathbf{1}_N)\le 1$, and by Lemma 1, $e_v(\mathbf{1}_N)= 1$.

Now suppose that $e_v(\mathbf{1}_N)= 1$. It implies that any sharp decomposition of $\mathbf{1}_N$, $\sum \alpha _S\mathbf{1}_S$, satisfies $S=N$ whenever $\alpha _S>0$. Thus, the decomposition is in fact $\mathbf{1}_N$ itself. $\square$

Proof of Claim 2

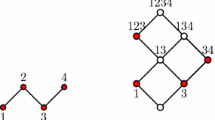
Let $x\in Q$ and $\sum \alpha _S\mathbf{1}_S$ be its sharp decomposition. W.l.o.g, $\alpha _{\{12\}}\le \alpha _{\{13\}},\alpha _{\{23\}}$. Thus we can replace $\alpha _{\{12\}}\mathbf{1}_{12}+\alpha _{\{13\}}\mathbf{1}_{13}+\alpha _{\{23\}}\mathbf{1}_{23}$ by $2(\alpha _{\{12\}}\mathbf{1}_{123}+(\alpha _{\{13\}}-\alpha _{\{12\}})\mathbf{1}_{13}+(\alpha _{\{23\}}-\alpha _{\{12\}})\mathbf{1}_{23})$.

We conclude that one may assume that in a sharp decomposition the coefficient of $\mathbf{1}_{12}$ is $0.$ Furthermore, based on the total balancedness of $v$, a similar argument would imply that no two coalitions with positive coefficients in the decomposition are disjoint. Thus, at most one singleton has a positive coefficient and the one that has a positive coefficient, if exists, is included in the other coalitions whose coefficients are positive.

We now show that there is $i\in N$ that is a member of all coalitions whose coefficients are positive. This shows that $e(x)= \max x$ and with the help of Theorem 1 completes the proof.

Case 1: $\alpha _{\{1\}}>0$. Then, $\alpha _{\{2\}}=\alpha _{\{3\}}=\alpha _{\{23\}}=0$, which means that $1\in S$ when $\alpha _{\{S\}}>0$. Case 2: $\alpha _{\{2\}}>0$. Then, $\alpha _{\{1\}}=\alpha _{\{3\}}=\alpha _{\{13\}}=0$ implying that $2\in S$ if $\alpha _{\{S\}}>0$. Case 3: $\alpha _{\{3\}}>0$. Similar to the previous case. Finally, Case 4: $\alpha _{\{i\}}=0$ for every $i\in N$. Since $\alpha _{\{12\}}=0$, $3\in S$ whenever $\alpha _{S}>0$. This completes the proof. $\square$

Proof of Claim 3

By Lovazc [10] (pp. 246–249), when $v$ is convex for any $x\in Q$, the Choquet decomposition is optimal. Thus, $e(x)=\max x$.$\square$

Proof of Claim 4

Assume that any sub-capacity of $v$ has a large core. This implies that $v$ is totally balanced. Thus, every sub-capacity of $v$ is totally balanced and has a large core. As such, any sub-capacity is exact (Sharkey [16]), implying that $v$ is convex (Biswas et al. [3]). By Claim 3, $v$ has the sandwich property.$\square$