Abstract
Optimization problems face random constraint violations when uncertainty arises in constraint parameters. Effective ways of controlling such violations include risk constraints, e.g., chance constraints and conditional Value-at-Risk constraints. This paper studies these two types of risk constraints when the probability distribution of the uncertain parameters is ambiguous. In particular, we assume that the distributional information consists of the first two moments of the uncertainty and a generalized notion of unimodality. We find that the ambiguous risk constraints in this setting can be recast as a set of second-order cone (SOC) constraints. In order to facilitate the algorithmic implementation, we also derive efficient ways of finding violated SOC constraints. Finally, we demonstrate the theoretical results via computational case studies on power system operations.






Similar content being viewed by others
Notes
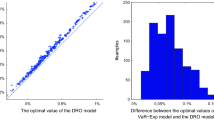
The ACC representation of Example 3.4.4 has typos and, for completeness, we present the corrected representation in Appendix C. We test the corrected ACC representation in this case study.
References
Ahmed, S., Papageorgiou, D.: Probabilistic set covering with correlations. Oper. Res. 61(2), 438–452 (2013)
Artzner, P., Delbaen, F., Eber, J.-M., Heath, D.: Coherent measures of risk. Math. Finance 9(3), 203–228 (1999)
Bergen, A.R., Vittal, V.: Power Systems Analysis, 2nd edn. Prentice Hall, Upper Saddle River (1999)
Bertsimas, D., Doan, X.V., Natarajan, K., Teo, C.-P.: Models for minimax stochastic linear optimization problems with risk aversion. Math. Oper. Res. 35(3), 580–602 (2010)
Bienstock, D., Chertkov, M., Harnett, S.: Chance-constrained optimal power flow: risk-aware network control under uncertainty. SIAM Rev. 56(3), 461–495 (2014)
Bookbinder, J.H., Tan, J.-Y.: Strategies for the probabilistic lot-sizing problem with service-level constraints. Manag. Sci. 34(9), 1096–1108 (1988)
Calafiore, G., El Ghaoui, L.: On distributionally robust chance-constrained linear programs. J. Optim. Theory Appl. 130(1), 1–22 (2006)
Charnes, A., Cooper, W., Symonds, G.: Cost horizons and certainty equivalents: an approach to stochastic programming of heating oil. Manag. Sci. 4(3), 235–263 (1958)
Cheng, J., Delage, E., Lisser, A.: Distributionally robust stochastic knapsack problem. SIAM J. Optim. 24(3), 1485–1506 (2014)
Delage, E., Ye, Y.: Distributionally robust optimization under moment uncertainty with application to data-driven problems. Oper. Res. 58(3), 595–612 (2010)
Dharmadhikari, S., Joag-Dev, K.: Unimodality, Convexity, and Applications. Elsevier, Amsterdam (1988)
El Ghaoui, L., Oks, M., Oustry, F.: Worst-case value-at-risk and robust portfolio optimization: a conic programming approach. Oper. Res. 51(4), 543–556 (2003)
Erdoğan, E., Iyengar, G.: Ambiguous chance constrained problems and robust optimization. Math. Program. 107(1), 37–61 (2006)
Esfahani, P. M., Kuhn, D.: Data-driven distributionally robust optimization using the Wasserstein metric: performance guarantees and tractable reformulations. Available on optimization-online. http://www.optimization-online.org/DB_FILE/2015/05/4899.pdf (2015)
Gade, D., Küçükyavuz, S.: Formulations for dynamic lot sizing with service levels. Nav. Res. Logist. 60(2), 87–101 (2013)
Gómez-Expósito, A., Conejo, A.J., Cañizares, C.: Electric Energy Systems: Analysis and Operation. CRC Press, Boca Raton (2008)
Hanasusanto, G. A.: Decision making under uncertainty: robust and data-driven approaches. Ph.D. thesis, Imperial College London (2015)
Hanasusanto, G. A., Roitch, V., Kuhn, D., Wiesemann, W.: Ambiguous joint chance constraints under mean and dispersion information. Available on optimization-online. http://www.optimization-online.org/DB_FILE/2015/11/5199.pdf (2015)
Henrion, R., Li, P., Möller, A., Steinbach, M.C., Wendt, M., Wozny, G.: Stochastic optimization for operating chemical processes under uncertainty. In: Grötschel, M., Krunke, S.O., Rambau, J. (eds.) Online Optimization of Large Scale Systems, pp. 457–478. Springer, Berlin (2001)
Henrion, R., Möller, A.: Optimization of a continuous distillation process under random inflow rate. Comput. Math. Appl. 45(1), 247–262 (2003)
Jiang, R., Guan, Y.: Data-driven chance constrained stochastic program. Math. Program. 158(1–2), 291–327 (2016)
Li, B., Jiang, R., Mathieu, J. L.: Distributionally robust risk-constrained optimal power flow using moment and unimodality information. In: 55th IEEE Conference on Decision and Control (CDC). IEEE (2016)
Miller, B., Wagner, H.: Chance constrained programming with joint constraints. Oper. Res. 13(6), 930–945 (1965)
Nemhauser, G.L., Wolsey, L.A.: Integer and Combinatorial Optimization. Wiley, Hoboken (1999)
Ozturk, U., Mazumdar, M., Norman, B.: A solution to the stochastic unit commitment problem using chance constrained programming. IEEE Trans. Power Syst. 19(3), 1589–1598 (2004)
Popescu, I.: A semidefinite programming approach to optimal-moment bounds for convex classes of distributions. Math. Oper. Res. 30(3), 632–657 (2005)
Popescu, I.: Robust mean–covariance solutions for stochastic optimization. Oper. Res. 55(1), 98–112 (2007)
Rockafellar, R.T., Uryasev, S.: Optimization of conditional value-at-risk. J. Risk 2, 21–42 (2000)
Rockafellar, R.T., Uryasev, S.: Conditional value-at-risk for general loss distributions. J. Bank. Finance 26(7), 1443–1471 (2002)
Scarf, H.: A min-max solution of an inventory problem. In: Arrow, K., Karlin, S., Scarf, H. (eds.) Studies in the Mathematical Theory of Inventory and Production, pp. 201–209. Stanford University Press, Palo Alto (1958)
Shapiro, A.: On duality theory of conic linear problems. In: Goberna, M.Á., López M.A. (eds.) Semi-Infinite Programming, pp. 135–165. Kluwer Academic Publishers, Dordrecht (2001)
Shapiro, A., Kleywegt, A.: Minimax analysis of stochastic problems. Optim. Methods Softw. 17(3), 523–542 (2002)
Sion, M.: On general minimax theorems. Pac. J. Math. 8(1), 171–176 (1958)
Stellato, B.: Data-driven chance constrained optimization. Master’s thesis, ETH Zürich (2014)
Van Parys, B. P. G., Goulart, P. J., Kuhn, D.: Generalized Gauss inequalities via semidefinite programming. Math. Program. 156(1–2), 271–302 (2015a)
Van Parys, B. P. G., Goulart, P. J., Morari, M.: Distributionally robust expectation inequalities for structured distributions. Available on optimization-online. http://www.optimization-online.org/DB_FILE/2015/05/4896.pdf (2015b)
Vandenberghe, L., Boyd, S., Comanor, K.: Generalized Chebyshev bounds via semidefinite programming. SIAM Rev. 49(1), 52–64 (2007)
Vrakopoulou, M., Margellos, K., Lygeros, J., Andersson, G.: A probabilistic framework for reserve scheduling and \(N-1\) security assessment of systems with high wind power penetration. IEEE Trans. Power Syst. 28(4), 3885–3896 (2013)
Wagner, M.: Stochastic 0–1 linear programming under limited distributional information. Oper. Res. Lett. 36(2), 150–156 (2008)
Wang, Q., Guan, Y., Wang, J.: A chance-constrained two-stage stochastic program for unit commitment with uncertain wind power output. IEEE Trans. Power Syst. 27(1), 206–215 (2012)
Wiesemann, W., Kuhn, D., Sim, M.: Distributionally robust convex optimization. Oper. Res. 62(6), 1358–1376 (2014)
Zimmerman, R.D., Murillo-Sánchez, C.E., Thomas, R.J.: MATPOWER: steady-state operations, planning, and analysis tools for power systems research and education. IEEE Trans. Power Syst. 26(1), 12–19 (2011)
Zymler, S., Kuhn, D., Rustem, B.: Distributionally robust joint chance constraints with second-order moment information. Math. Program. 137(1–2), 167–198 (2013a)
Zymler, S., Kuhn, D., Rustem, B.: Worst-case value at risk of nonlinear portfolios. Manag. Sci. 59(1), 172–188 (2013b)
Acknowledgements
This research has been supported in part by the National Science Foundation (NSF) under Grants CMMI-1555983 and CCF-1442495.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix A: proof of Observation 2
Proof
As \(f^k_+(z) = \bigl (\frac{\alpha }{\alpha + 1}\bigr )(1 - k^{-\alpha -1})z - (1 - k^{-\alpha }) \beta \), we have
for all \(k \ge 1\). As \([f^{k+1}_+(z)]_+ \ge 0\) for all \(z \in \mathbb {R}\), to show that \([f^{k+1}_+(z)]_+ \ge [f^k_+(z)]_+\), it suffices to prove that \([f^{k+1}_+(z)]_+ \ge f^k_+(z)\) for all \(z \in \mathbb {R}\). First, as \(\beta \le 0\) and \(\frac{1 - k^{-\alpha }}{1 - k^{-\alpha -1}}\) increases in k, we have \(\bigl (\frac{\alpha +1}{\alpha }\bigr ) \bigl (\frac{1 - k^{-\alpha }}{1 - k^{-\alpha -1}}\bigr ) \beta \ge \bigl (\frac{\alpha +1}{\alpha }\bigr ) \bigl (\frac{1 - (k+1)^{-\alpha }}{1 - (k+1)^{-\alpha -1}}\bigr ) \beta \), i.e., \(z_0(k) \ge z_0(k+1)\). It follows that, when \(z < z_0(k)\), \(f^k_+(z) \le 0\) and hence \([f^{k+1}_+(z)]_+ \ge f^k_+(z)\). Second, when \(z \ge z_0(k)\), \(f^{k+1}_+(z) \ge 0\) because \(z \ge z_0(k) \ge z_0(k+1)\) and \(f^{k+1}_+(z)\) increases in z. As both \(f^k_+(z)\) and \(f^{k+1}_+(z)\) are affine functions of z, we have \(f^{k+1}_+(z) = f^{k+1}_+(z_0(k)) + (\frac{\alpha }{\alpha + 1})(1 - (k+1)^{-\alpha -1})(z - z_0(k))\) and \(f^k_+(z) = (\frac{\alpha }{\alpha + 1})(1 - k^{-\alpha -1})(z - z_0(k))\) for \(z \ge z_0(k)\). It follows that \(f^{k+1}_+(z) - f^k_+(z) = f^{k+1}_+(z_0(k)) + (\frac{\alpha }{\alpha + 1})[k^{-\alpha -1} - (k+1)^{-\alpha -1}](z - z_0(k)) \ge 0\). Hence, \([f^{k+1}_+(z)]_+ \ge f^k_+(z)\) when \(z \ge z_0(k)\) and the proof is complete. \(\square \)
Appendix B
For random variable Z and constant \(\beta \in \mathbb {R}\), we make the following observation on the worst-case expectation \(\sup _{{\mathbb P}_Z \in \mathcal {D}(\mu _0, \Sigma _0)} \mathbb {E}_{{\mathbb P}_Z}[Z-\beta ]_+\). Note that this observation can be made following the derivations in [30], and we present a proof below for completeness.
Observation 3
Given \(\beta \in {\mathbb R}\), we have
Proof
We represent \(\sup _{{\mathbb P}_Z \in \mathcal {D}(\mu _0, \Sigma _0)} \mathbb {E}_{{\mathbb P}_Z}[Z-\beta ]_+\) as the following optimization problem
The weak duality between (P) and (D), i.e., \(v_D \le v_P\), holds because \(\mu _0 p + \Sigma _0 q + r = \mathbb {E}_{{\mathbb P}_Z}[qZ^2 + pZ + r] \le \mathbb {E}_{{\mathbb P}_Z}[Z-\beta ]_+\) for any feasible solution (q, p, r) to (D) and feasible solution \({\mathbb P}_Z\) to (P). Now we prove the strong duality by constructing two feasible solutions to (P) and (D), respectively, that have the same objective value. On the one hand, the primal solution \(\hat{{\mathbb P}}_Z\) is supported on two points \(z_1\) and \(z_2\) with probability masses \(p_1\) and \(p_2\), respectively, where \(\Delta = \sqrt{(\beta - \mu _0)^2 + (\Sigma _0 - \mu _0^2)}\) and
We have \(p_1, p_2 \ge 0\) because \(\Delta \ge |\beta - \mu _0|\). Meanwhile, we have
and
Hence, \(\hat{{\mathbb P}}_Z\) is feasible to (P). On the other hand, the dual solution \((\hat{q}, \hat{p}, \hat{r})\) is such that
Hence, \(\hat{q}z^2 + \hat{p}z + \hat{r} = \frac{1}{4\Delta }(z + \Delta - \beta )^2\). It follows that \(\hat{q}z^2 + \hat{p}z + \hat{r} \ge 0\) for all \(z \in {\mathbb R}\). Meanwhile, \((\hat{q}z^2 + \hat{p}z + \hat{r}) - (z - \beta ) = \frac{1}{4\Delta }(z - \beta - \Delta )^2 \ge 0\), i.e., \(\hat{q}z^2 + \hat{p}z + \hat{r} \ge z - \beta \). Thus, \(\hat{q}z^2 + \hat{p}z + \hat{r} \ge [z-\beta ]_+\) and so \((\hat{q}, \hat{p}, \hat{r})\) is feasible to (D).
Finally, the primal objective value associated with \(\hat{{\mathbb P}}_Z\) is \(p_2(z_2 - \beta ) = \frac{(\mu _0 - \beta + \Delta )\Delta }{2\Delta } = \frac{1}{2}(\Delta - \beta + \mu _0)\). Meanwhile, the dual objective value associated with \((\hat{q}, \hat{p}, \hat{r})\) is
which coincides with the primal objective value associated with \(\hat{{\mathbb P}}_Z\). \(\square \)
Appendix C: corrected ACC representation of Example 3.4.4 in [17]
The ACC representation (3.50) in Example 3.4.4 in [17] has typos and is corrected as follows:
Rights and permissions
About this article
Cite this article
Li, B., Jiang, R. & Mathieu, J.L. Ambiguous risk constraints with moment and unimodality information. Math. Program. 173, 151–192 (2019). https://doi.org/10.1007/s10107-017-1212-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10107-017-1212-x
Keywords
- Ambiguity
- Chance constraints
- Conditional Value-at-Risk
- Second-order cone representation
- Separation
- Golden section search