Abstract
In the linked open data cloud, the biggest open data graph that currently exists, a remarkable percentage of data are unnamed resources, also called blank nodes. Several fundamental tasks, such as graph isomorphism checking and RDF data versioning, require computing a map between the sets of blank nodes of two graphs. This map aims at minimizing the delta size, i.e. the number of change operations that are required to make the graphs isomorphic. Computing the optimal map is NP-Hard in the general case, and various approximation algorithms have been proposed. In this work, we propose a novel radius-aware signature-based algorithm that is not restricted to the direct neighborhood of the compared blank nodes. Contrary to the older algorithms, the proposed algorithm manages to decrease the deviation from the optimal solution even for graphs that contain connected blank nodes in large and dense structures. The conducted experiments over real and synthetically generated datasets (including datasets from the Billion Triple Challenge 2012 and 2014) show the significantly smaller deltas. For isomorphism checking (simple RDF equivalence), with a wise configuration of radius, the proposed algorithm achieves optimality for \(100\,\%\) of the datasets, while in non-isomorphic datasets the deltas are on average 50–75 % smaller than those of the previous algorithms. Finally, the trade-off between radius, deviation from the optimum and time efficiency is analyzed.

















Similar content being viewed by others
References
Ahn J, Im D-H, Eom J-H, Zong N, Kim H-G (2014) G-diff: a grouping algorithm for RDF change detection on MapReduce. In: 4th joint international conference on semantic technology (JIST-2014), Chiang Mai, Thailand, November, 2014, pp 230–235
Berners-Lee T, Connolly D (2004) Delta: an ontology for the distribution of differences between RDF graphs. http://www.w3.org/DesignIssues/Diff (version: 2004-05-01)
Carroll JJ (2002) Matching RDF graphs. In: 1st international semantic web conference (ISWC-2002), Sardinia, Italy, June 2002, pp 5–15
Chen L, Zhang H, Chen Y, Guo W (2012) Blank nodes in RDF. J Softw 27(9):1993–1999
Costabello L (2014) Error-tolerant RDF subgraph matching for adaptive presentation of linked data on mobile. Semant Web Trends Chall 2014:36–51
Cyganiak R, Wood D, Lanthaler M (2014) RDF 1.1 concepts and abstract syntax. W3C Recommendation. http://www.w3.org/TR/rdf11-concepts/
Dorneles CF, Gonçalves R, dos Santos Mello R (2011) Approximate data instance matching: a survey. Knowl Inf Syst 27(1):1–21
Engmann D, Maßmann S (2007) Instance matching with COMA++. In: Workshop on Datenbanksysteme in Business, Technologie und Web (BTW-2007), pp 28–37
Guo Y, Pan Z, Heflin J (2005) LUBM: a benchmark for OWL knowledge base systems. J Web Semant 3(2–3):158–182
Harary F (1969) Graph theory. Addison-Wesley, Reading
Harth A (2012) Billion triples challenge data set. Downloaded from http://km.aifb.kit.edu/projects/btc-2012/
Hogan A (2015) Skolemising blank nodes while preserving isomorphism. In: 24th international world wide web conference (WWW-2015), pp 430–440
Hogan A, Arenas M, Mallea A, Polleres A (2014) Everything you always wanted to know about blank nodes. J Web Semant 27:42–69
Käfer T, Harth A (2014) Billion triples challenge data set. Downloaded from http://km.aifb.kit.edu/projects/btc-2014/
Kirsten T, Kolb L, Hartung M, Groß A, Köpcke H, Rahm E (2010) Data partitioning for parallel entity matching. In: CoRR, abs/1006.5309. http://arxiv.org/abs/1006.5309
Kjrulff UB (1990) Triangulation of graphs–algorithms giving small total state space. In: Technical report, Department of Computer Science, Aalborg University
Klein MCA, Fensel D, Kiryakov A, Ognyanov D (2002) Ontology versioning and change detection on the web. In: 13th international conference on knowledge engineering and knowledge management—ontologies and the semantic web (EKAW-2002), 2002, pp 197–212
Knuth M, Reddy D, Dimou A, Vahdati S, Kastrinakis G (2015) Towards linked data update notifications. In: Workshop on negative or inconclusive results in semantic web (NoISE’15), Portoroz, Slovenia, June 2015, pp 537–551
Lantzaki C, Tzitzikas Y (2014) Tasks that require or can benefit from matching blank nodes. In: CoRR, abs/1410.8536. http://arxiv.org/abs/1410.8536
Lantzaki C, Yannakis T, Tzitzikas Y, Analyti A (2014) Generating synthetic RDF data with connected blank nodes for benchmarking. In: 11th extended semantic web conference (ESWC-2014), Anissaras Hersonissou, Crete, Greece, May, 2014, pp 192–207
Mallea A, Arenas M, Hogan A, Polleres A (2011) On blank nodes. In: 10th international semantic web conference (ISWC-2011), Bonn Germany, October 2011, pp 421–437
Noy NF, Musen MA (2002) Promptdiff: a fixed-point algorithm for comparing ontology versions. In: 8th national conference on artificial intelligence and 14th conference on innovative applications of artificial intelligence, 2002, pp 744–750
Pichler R, Polleres A, Wei F, Woltran S (2008) dRDF: entailment for domain-restricted RDF. IN: 5th european semantic web conference (ESWC-2008), Tenerife, Spain, November 2008, pp 200–214
Ramachandramurthi S (1997) The structure and number of obstructions to treewidth. SIAM J Discret Math 10(1):146–157
Tummarello G, Morbidoni C, Bachmann-Gmür R, Erling O (2007) RDFSync: efficient remote synchronization of RDF models. In: 6th international semantic web conference (ISWC-2007) and 2nd Asian semantic web conference (ASWC-2007), Busan, Korea, November 2007, pp 537–551
Tzitzikas Y, Alloca C, Bekiari C, Marketakis Y, Fafalios P, Doerr M, Minadakis N, Patkos T, Candela L (2013) Integrating heterogeneous and distributed information about marine species through a top level ontology. In: Proceedings of the 7th metadata and semantic research conference (MTSR’13), Thessaloniki, Greece, November 2013
Tzitzikas Y, Lantzaki C, Zeginis Di (2012) Blank node matching and RDF/S comparison functions. IN: 11th international semantic web conference (ISWC-2012), Boston, USA, November 2012, pp 591–607
Volkel M, Groza T (2006) SemVersion: RDF-based ontology versioning system IADIS international conference WWW/Internet (ICWI-2006)
Zeginis D, Tzitzikas Y, Christophides V (2011) On computing deltas of RDF/S knowledge bases. ACM Trans Web (TWEB) 5(3):14
Acknowledgments
We would like to thank Yannis Marketakis for helping us in formatting the manuscript.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix 1: Algorithm signature

Algorithm Signature (Algorithm 5) takes as input a bnode b and its graph G and produces sign(b). Firstly, at line 2, it classifies the triples of DNG(b, G) into the three categories, Class(b), In(b) and Out(b), as given in Definition 4, and for each category, an ordered set is initialized (line 3), i.e. \(L_{Class(b)}\), \(L_{In(b)}\), \(L_{Out(b)}\), respectively. These ordered sets store one pair of the form (\(l_b(t_i)\), \(b'\)) for each triple \(t_i\) that is part of the respective category (line 7), where \(b'\) is the adjacent node of b through the triple \(t_i\) (line 6) and \(l_b(t_i)\) is the label of \(t_i\) in terms of b, as defined in Definition 5. Each set is sorted lexicographically in terms of its labels (line 8).
As an optimization to the algorithm given in (Tzitzikas et al. [27], the algorithm also creates a list L, which is useful to produce counters for the adjacent bnodes of b and therefore ensures the deterministic construction of the signature. In particular, L stores one pair of the form (labels, \(b'\)) for each adjacent bnode \(b'\), where labels is a strict concatenation of all the labels of the triples that contain both b and \(b'\). Lines 9–19 construct each pair of L by traversing the already ordered sets \(L_{Class(b)}\), \(L_{In(b)}\), \(L_{Out(b)}\). For each pair (\(l, b'\)) of these lists if \(b'\) is not yet part of L a new pair (\(l, b'\)) is added to L (line 15–16). Alternatively, if a pair (\(x, b'\)) already exists in L (line 11), the label l is concatenated with x and the new pair replaces the old one (lines 12–13). Notice that delimiters are also added between the labels (line 13) and between the categories (line 17–19). Afterward, L is sorted in terms of its labels (line 20) and by this new contribution the adjacent nodes of b are ordered in a deterministic way.
Finally, the ordered sets \(L_{Class(b)}\), \(L_{In(b)}\), \(L_{Out(b)}\) are once more traversed (lines 21–22). For each pair (\(l, b'\)) of these sets l is concatenated to the signature sign(b) (line 23). In case the adjacent node \(b'\) is a bnode (line 24) the position of \(b'\) in L is also added next to l (line 25). In order to ensure a deterministic construction of the signature, delimiters are also added between the labels (line 26) and between the categories (line 27). The signature sign(b) is returned.
Appendix 2: Proofs
Proposition 1
(Bnodes in BComponents) Each bnode \(b_1 \in B_1\) is part of exactly one BComponent, denoted as BC(b) (obviously \(BC(b) \subseteq G_1\)).
Proof
From Definition 6, we get that a BComponent is a maximal set of connected bbtriples. A node of a graph cannot be part of two different maximal sets. \(\square \)
Proposition 2
Properties of Maximum Neighborhood Graph
-
p1:
\(\exists ~r_{max} \ge 1\) s.t. \(\forall ~r \ge r_{max} RNG(b,r,G) = RNG(b,r_{max},G) = MNG(b,G)\)
-
p2:
\(MNG(b,G) \supseteq BC(b)\)
-
p3:
\(nodes(MNG(b,G)) \cap B = nodes(BC(b))\)
Proof
-
p1:
It is clear from Definition 8 that \(r_{max}\) gives the maximum element of the Radius Neighborhood Graph and therefore each higher value will not make a difference.
-
p2:
It holds because MNG(b, G) contains not only all the bbtriples of the BComponent, but also all the btriples that are directly connected to the bbtriples.
-
p3:
Since we get from p2 of Proposition 2 that MNG(b, G) is a superset of a BComponent, it entails that it contains all the bnodes of the BComponent and in addition it cannot contain more bnodes.\(\square \)
Proposition 3
Properties of Matches
-
p1:
\(\approx _{r'}\ \subseteq \ \approx _{r}\), \(\forall r\), \(r'\), where \(r' \ge r \ge 1\)
-
p2:
\(\approx _{r}^{r'} \subseteq \approx _{r'}\), \(\forall r\), \(r'\), where \(r' \ge r \ge 1\)
-
p3:
\(\approx _{r}^{r_b} \subseteq \approx _{r}^{r_a}\), \(\forall r_a\), \(r_b\), where \(r_b \ge r_a \ge 1\)
-
p4:
\(\approx _{r}^{r_b} \subseteq \approx _{r'}^{r_b}\), \(\forall r_b\), r, \(r'\) where \(1 \le r_b \le r \le r'\)
-
p5:
\(\approx _r^B\subseteq \approx _r\), \(\forall r \ge 1\)
-
p6:
\(b_1 \approx _r^B b_2 \Rightarrow \exists m\):\(nodes(BC(b_1)) \rightarrow nodes(BC(b_2))\) s. t. \(b_3 \approx _{r} m(b_3)\), \(\forall b_3 \in nodes(BC(b_1))\)
-
p7:
\(\approx _{r_a}^B\subseteq \approx _{r_b}^B\), \(\forall r_a\), \(r_b\), where \(1 \le r_a \le r_b\)
Proof
-
p1:


 . As a result, we get \(\approx _{r'} \subseteq \approx _{r}\).
. As a result, we get \(\approx _{r'} \subseteq \approx _{r}\). -
p2:
 . As a result, we get \(\approx _{r}^{r'} \subseteq \approx _{r'}\). As a result, we get \(\approx _{r}^{r'} \subseteq \approx _{r'}\).
. As a result, we get \(\approx _{r}^{r'} \subseteq \approx _{r'}\). As a result, we get \(\approx _{r}^{r'} \subseteq \approx _{r'}\). -
p3:

 . As a result, we get \(\approx _{r}^{r_b} \subseteq \approx _{r}^{r_a}\).
. As a result, we get \(\approx _{r}^{r_b} \subseteq \approx _{r}^{r_a}\). -
p4:
 and
and  . As a result, we get \(\approx _{r}^{r_b} \subseteq \approx _{r'}^{r_b}\).
. As a result, we get \(\approx _{r}^{r_b} \subseteq \approx _{r'}^{r_b}\). -
p5:
 . As a result,\(\approx _r^B\subseteq \approx _r\). As a result, we get \(\approx _r^B\subseteq \approx _r\).
. As a result,\(\approx _r^B\subseteq \approx _r\). As a result, we get \(\approx _r^B\subseteq \approx _r\). -
p6:
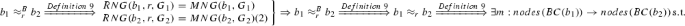
 . Since \(RNG(b_1,r,G_1)\), \(RNG(b_2,r,G_2)\) are equivalent, it follows that \(RNG(b,r,G_1) \equiv RNG(b',r,G_2)\). This implies that
. Since \(RNG(b_1,r,G_1)\), \(RNG(b_2,r,G_2)\) are equivalent, it follows that \(RNG(b,r,G_1) \equiv RNG(b',r,G_2)\). This implies that  s.t. \(b' \approx _{r} m(b')\), \(\forall b' \in nodes(BC(b_1))\).
s.t. \(b' \approx _{r} m(b')\), \(\forall b' \in nodes(BC(b_1))\). -
p7:
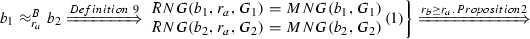
\(\begin{array}{rcl} RNG(b_1,r_b,G_1) &{}=&{} MNG(b_1,G_1) \\ RNG(b_2,r_b ,G_2) &{}=&{} MNG(b_2,G_2) \end{array}(2)\)
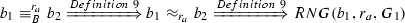 , \(RNG(b_2, r_a, G_2)\) are equivalent
, \(RNG(b_2, r_a, G_2)\) are equivalent 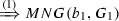 , \(MNG(b_2,G_2)\) are equivalent
, \(MNG(b_2,G_2)\) are equivalent  , \(RNG(b_2, r_b, G_2)\) are equivalent
, \(RNG(b_2, r_b, G_2)\) are equivalent  . As a result, \(\approx _{r_a}^B \subseteq \approx _{r_b}^B\).\(\square \)
. As a result, \(\approx _{r_a}^B \subseteq \approx _{r_b}^B\).\(\square \)
Proposition 4
(DNG and Signatures) For two bnodes \(b_1 \in B_1\) and \(b_2 \in B_2\) it holds that \(DNG(b_1, G_1) \equiv DNG(b_2, G_2) \Leftrightarrow sign(b_1) = sign(b_2)\).
Proof
Let us first show that if \(DNG(b_1, G_1) \equiv DNG(b_2, G_2)\) then \(sign(b_1) = sign(b_2)\). Since the Direct Neigborhood Graphs are equivalent, we get from Definition 2 that there is a bijection m between the terms of the two graphs s.t. \(m(u) = u \forall u \in U \cup L\) and m maps bnodes to bnodes so that it holds that a triple (s, p, o) \(\in DNG(b_1,G_1)\) if and only if a triple (m(s), p, m(o)) \(\in DNG(b_2,G_2)\). Thus, for each triple t = (s, p, o) \(\in DNG(b_1,G_1)\) there is a triple \(t'\) = (m(s), p, m(o)) \(\in DNG(b_2,G_2)\). It holds that \(l_{b_1}(t) = l_{b_2}(t')\), since if s is a Uri or a literal, \(m(s) =s\). Same goes for o. If s is a bnode then m(s) is also a bnode and the representation for all the bnodes is the character \(\bullet \). Same goes for o. Both signatures \(sign(b_1)\) and \(sign(b_2)\) are going to have the same substrings, but now we have to prove that these substrings will be ordered in the same way. As long as the DNGs are equivalent, the subgraphs of their incoming and outgoing triples are also equivalent. So, each set of substrings is the same, it is sorted lexicographically in the same way (\(L_{Class(b_1)} = L_{Class(b_2)}\) and so on), and it is separated with the same special characters in the same positions. Regarding the counters that follow the bnodes, as soon as both the lists (L) of \(b_1\) and \(b_2\) contain the same strings the ordering will be the same and by extension the given counters will also be the same inside the signatures. We get that \(sign(b_1) = sign(b_2)\).
Let us now show that if \(sign(b_1) = sign(b_2)\) then \(DNG(b_1, G_1) \equiv DNG(b_2, G_2)\). If we separate the two signatures according to the delimiters, then we get all the triple representations of both signatures. Since the signatures are the same, their triple representations are also the same, and by extension both \(b_1\) and \(b_2\) have the same triples in their Direct Neighborhoods. Since the numbering of the adjacent bnodes is the same, the map m between the adjacent bnodes of \(b_1\) and \(b_2\) will form a bijection that guarantees equivalence. From the above, we get that the DNGs of \(b_1\) and \(b_2\) are equivalent. \(\square \)
Proposition 5
(Upper Bound of “Unnamed” Delta) For any map \(M_x\) between two graphs \(G_1\) and \(G_2\), it holds that \(|\Delta ^{{{\mathcal {B}}}}_e(G_1 \rightarrow G_2, M_x)| \le |btriples(G_1)| + |btriples(G_2)| + |bbtriples(G_1)| + |bbtriples(G_2)|\).
Proof
In the worst case (e.g. if all bnodes are treated as different, equivalently if \(M_x = \emptyset \)), the delta will require the deletion of all the triples in \(G_1\) that bnodes participate (i.e. all the btriples and bbtriples) and the addition of all the triples in \(G_2\) that bnodes participate. \(\square \)
Proposition 6
Deviation from Optimal for Equivalent Graphs of SIGN and r-SIGN
If \(G_1 \equiv G_2\) then
-
(i)
\(|\Delta ^{{{\mathcal {B}}}}_e(G_1 \rightarrow G_2, M_{SIGN})| \le |bbtriples(G_1)| + |bbtriples(G_2)|\).
-
(ii)
\(|\Delta ^{{{\mathcal {B}}}}_e(G_1 \rightarrow G_2, M_{rSIGN})| \le |bbtriples(G_1)| + |bbtriples(G_2)|\).
This upper bound is actually upper bound of the deviation from the optimal, since the optimal \(\Delta ^{{{\mathcal {B}}}}_e\) is empty.
Proof
(i)  s.t. \(\forall (b_1,b_2) \in M\) it holds that
s.t. \(\forall (b_1,b_2) \in M\) it holds that  it holds that \(sign(b_1) = sign(b_2)\) (1). Since (1) holds we get that SIGN will find for each \(b_1 \in B_1\) a \(b_2 \in B_2\), such that \(sign(b_1) = sign(b_2)\). Therefore, \(M_{SIGN}\) will contain only Exact Matches and \(\forall (b_1,b_2) \in M_{SIGN}\) it holds that \((b_1,p,o) \in G_1\) and \((b_2,p,o) \in G_2\) and \((s,p,b_1) \in G_1\) and \((s,p,b_2) \in G_2\). In other words, we get that \(\forall (b_1,b_2) \in M_{SIGN}\) it holds
it holds that \(sign(b_1) = sign(b_2)\) (1). Since (1) holds we get that SIGN will find for each \(b_1 \in B_1\) a \(b_2 \in B_2\), such that \(sign(b_1) = sign(b_2)\). Therefore, \(M_{SIGN}\) will contain only Exact Matches and \(\forall (b_1,b_2) \in M_{SIGN}\) it holds that \((b_1,p,o) \in G_1\) and \((b_2,p,o) \in G_2\) and \((s,p,b_1) \in G_1\) and \((s,p,b_2) \in G_2\). In other words, we get that \(\forall (b_1,b_2) \in M_{SIGN}\) it holds  their union is also equivalent or else \(\forall (b_1,b_2) \in M_{SIGN} btriples(b_1) \equiv btriples(b_2)\). Thus, we get that \(|\Delta ^{{{\mathcal {B}}}}_e(G_1 \rightarrow G_2, M_{SIGN}| \le |bbtriples(G_1)| + |bbtriples(G_2)|\).
their union is also equivalent or else \(\forall (b_1,b_2) \in M_{SIGN} btriples(b_1) \equiv btriples(b_2)\). Thus, we get that \(|\Delta ^{{{\mathcal {B}}}}_e(G_1 \rightarrow G_2, M_{SIGN}| \le |bbtriples(G_1)| + |bbtriples(G_2)|\).
(ii) Since \(G_1\) and \(G_2\) are equivalent for each \(b_1\) in nodes(BC1), where \(BC_1\) is a BComponent of \(G_1\), rSIGN will find and will make either
-
(1)
an Exact r-Match with a bnode \(b_2\) in nodes(BC2), where \(BC_2\) is a BComponent of \(G_2\) or
-
(2)
a BC r-Match with a bnode \(b_2\) in nodes(BC2) where \(BC_2\) is a BComponent of \(G_2\) .
In case 1) then from the Proof of (i) we know that the \(btriples(b1) \equiv btriples(b2)\) and only the \(bbtriples(b1) \cup bbtriples(b2)\) are possibly in Delta.
In case 2) the BComponent Match ensures that there is a map \(m: nodes(BC1) \rightarrow nodes(BC2)\) such that each \((b_1,b_2) \in m\) makes an exact Match. Again from i) we get that \(btriples(b_1) \equiv btriples(b_2)\). Thus again only \(bbtriples(b_1)\) and \(bbtriples(b_2)\) are possibly in Delta. \(\square \)
Proposition 7
(SIGN vs r-SIGN if no connected bnodes) If \(G_1\) and \(G_2\) have no connected bnodes, i.e. none of them contains any bbtriple, then \(M_{SIGN} = M_{rSIGN}\) for any \(r \ge 2\).
Proof
The constructed signatures will be the same. What SIGN reports as Exact Match is what r-SIGN reports as BC r-Match. The Closest Matches of SIGN are the same those of r-SIGN since they will be constructed in the same way. \(\square \)
Proposition 8
(SIGN vs r-SIGN) If \(G_1 \equiv G_2\) then r-SIGN will find the maximum in diameter (say dmax) BC dmax-Match if it is unique, and \(r \ge dmax\). This is not always true for SIGN.
Proof
r-SIGN (for \(r \ge dmax\)) first looks for BC r-Matches. It will always find the BC dmax-Match and report it in \(M_{rSIGN}\). It is not possible to miss it, because there is not any other BComponent with the same or bigger diameter. Instead, SIGN makes only exact matches, and therefore, a different matching could occur. \(\square \)
Rights and permissions
About this article
Cite this article
Lantzaki, C., Papadakos, P., Analyti, A. et al. Radius-aware approximate blank node matching using signatures. Knowl Inf Syst 50, 505–542 (2017). https://doi.org/10.1007/s10115-016-0945-9
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10115-016-0945-9






 . As a result, we get
. As a result, we get  . As a result, we get
. As a result, we get 
 . As a result, we get
. As a result, we get  and
and  . As a result, we get
. As a result, we get  . As a result,
. As a result,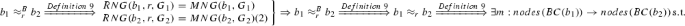
 . Since
. Since  s.t.
s.t. 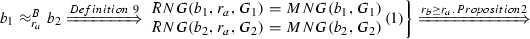
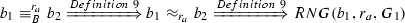 ,
, 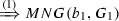 ,
,  ,
,  . As a result,
. As a result,