A successive linear programming algorithm with non-linear time series for the reservoir management problem

Abstract

This paper proposes a multi-stage stochastic programming formulation based on affine decision rules for the reservoir management problem. Our approach seeks to find a release schedule that balances flood control and power generation objectives while considering realistic operating conditions as well as variable water head. To deal with the non-convexity introduced by the variable water head, we implement a simple, yet effective, successive linear programming algorithm. We also introduce a novel non-linear inflow representation that captures serial correlation of arbitrary order. We test our method on a small real river system and discuss policy implications. Our results namely show that our method can decrease flood risk and increase production compared to the historical decisions, albeit at the cost of reduced final storages.

Appendices

Appendix

1.1 Counterexample showing that $\varXi _t$ is generally non-convex

We show that in general, $\varXi _t$ is not convex for an arbitrary $t \in {\mathbb {T}}$. Consider the following instance:

$$\begin{aligned}&V = \left( \begin{array}{cc} 1 &{} 0 \\ -1 &{} 1 \end{array} \right) \\&v_t=u_t=(0,0)^{\top } \\&P\, = \{ \varrho \in {\mathbb {R}}^L : -1 \leqslant \varrho _l \leqslant 1, \forall l =1,\ldots ,L; \, \sum _{i=1}^L |\varrho _i| \leqslant \sqrt{L}\} \\&L=2. \end{aligned}$$

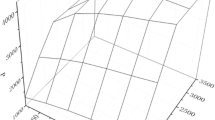
Figure 10 displays $\varXi _t=\{ \xi \in {\mathbb {R}}^L : \exists \varrho \in P, \xi _l = \exp ( V_l^{\top } \varrho ), \forall l=1,\ldots ,L\}$ and illustrates that $\varXi _t$ is in general not convex.

Fig. 10

Non convex uncertainty set

For a slightly more formal demonstration, it is possible to show that given the two points ${\hat{\varrho }}_1=(1-\sqrt{2},1)^{\top } \in P$ and ${\hat{\varrho }}_2=(\sqrt{2}-1,1)^{\top }\in P$ illustrated in Fig. 10 as well as $\lambda =\frac{1}{2}$, there exists no $\varrho \in P$ such that:

$$\begin{aligned} \lambda&\left( \begin{array}{c} e^{V_1^{\top }{\hat{\varrho }}_1} \\ e^{V_2^{\top }{\hat{\varrho }}_1} \end{array} \right) + (1-\lambda ) \left( \begin{array}{c} e^{V_1^{\top }{\hat{\varrho }}_2} \\ e^{V_2^{\top }{\hat{\varrho }}_2} \end{array} \right) = \left( \begin{array}{c} e^{V_1^{\top }\varrho } \\ e^{V_2^{\top }\varrho } \end{array} \right) . \end{aligned}$$

(34)

Equivalently, we can show that $\forall \varrho \in P$,

$$\begin{aligned} \left\| \left( \begin{array}{c} e^{V_1^{\top }\varrho } \\ e^{V_2^{\top }\varrho } \end{array} \right) - \lambda \left( \begin{array}{c} e^{V_1^{\top }{\hat{\varrho }}_1} \\ e^{V_2^{\top }{\hat{\varrho }}_1} \end{array} \right) + (1-\lambda ) \left( \begin{array}{c} e^{V_1^{\top }{\hat{\varrho }}_2} \\ e^{V_2^{\top }{\hat{\varrho }}_2} \end{array} \right) \right\| _{\infty } > 0. \end{aligned}$$

This can be shown by solving the following linear program and observing that its optimal value is strictly larger than 0:

$$\begin{aligned}&\quad \displaystyle \mathop {{{\mathrm{min}}}}\limits _{\varrho ^+\geqslant 0,\varrho ^-\geqslant 0,t \geqslant 0} \quad \; \; t \\&\quad \text{ s. } \text{ t. } \quad \quad \sum _{i=1}^2 (\varrho _i^+ + \varrho _i^- ) \leqslant \sqrt{2} \\&\quad \quad \quad \quad \, \quad \varrho _{i}^+ + \varrho _i^- \leqslant 1, \quad \forall i =1,2 \\&\quad \quad \quad \quad \quad \, V_i^{\top } (\varrho ^+ - \varrho ^-) -l_{i}^{\lambda } \leqslant t, \quad i=1,2 \\&\quad \quad \quad \quad \quad \, l_{i}^{\lambda } - V_i^{\top } (\varrho ^+ - \varrho ^-) \leqslant t, \quad i=1,2, \end{aligned}$$

where $l_{i}^{\lambda } = ln(\lambda e^{V_i^{\top }{\hat{\varrho }}_1 } + (1-\lambda ) e^{V_i^{\top }{\hat{\varrho }}_2} )$ is a known constant.

First order Taylor approximation of the composite risk

We first fix ${\text {E} \left[ {\mathcal {P}}_{i,t+l}(\xi ) {\mathcal {H}}_{i,t+l}(\xi ) |\mathcal {G}_{t-1} \right] } \equiv F_{i,t+l}({\mathcal {H}}_{i,t+l},{\mathcal {P}}_{i,t+l})$ where ${\mathcal {H}}_{i,t+l}=({\mathcal {H}}^0_{i,t+l},{\mathcal {H}}^{t+1}_{i,t+l},\ldots ,{\mathcal {H}}^{t+L-1}_{i,t+l})^{\top } \in {\mathbb {R}}^L$ and ${\mathcal {P}}_{i,t+l}=({\mathcal {P}}^0_{i,t+l},{\mathcal {P}}^{t+1}_{i,t+l},\ldots ,{\mathcal {P}}^{t+L-1}_{i,t+l})^{\top }\in {\mathbb {R}}^L$. Given the point $(\hat{{\mathcal {H}}}_{i,t+l}^{\top } ,\hat{{\mathcal {P}}}_{i,t+l}^{\top } )^{\top } \in {\mathbb {R}}^{2L }$, we then obtain:

$$\begin{aligned}&F_{i,t+l}({\mathcal {H}}_{i,t+l},{\mathcal {P}}_{i,t+l}) \approx F_{i,t+l}(\hat{{\mathcal {H}}}_{i,t+l},\hat{{\mathcal {P}}}_{i,t+l}) \nonumber \\&\quad + \hat{{\mathcal {H}}}_{i,t+l}^0 ({{\mathcal {P}}}_{i,t+l}^0-\hat{{\mathcal {P}}}_{i,t+l}^0 ) \nonumber \\&\quad + \sum _{k=0}^{L-1} \hat{{\mathcal {H}}}_{i,t+l}^0 ({{\mathcal {P}}}_{i,t+l}^{t+k}-\hat{{\mathcal {P}}}_{i,t+l}^{t+k} )\text {E} \left[ \xi _{t+k} |\mathcal {G}_{t-1} \right] \nonumber \\&\quad + \sum _{k=0}^{L-1} \hat{{\mathcal {H}}}_{i,t+l}^{k} ({{\mathcal {P}}}_{i,t+l}^0-\hat{{\mathcal {P}}}_{i,t+l}^{0}) \text {E} \left[ \xi _{t+k} |\mathcal {G}_{t-1} \right] \nonumber \\&\quad + \sum _{m=0}^{L-1} \sum _{k=0}^{L-1} \hat{{\mathcal {H}}}_{i,t+l}^{t+m} ({{\mathcal {P}}}_{i,t+l}^{t+k}-\hat{{\mathcal {P}}}_{i,t+l}^{t+k} ) \text {E} \left[ \xi _{t+m} \xi _{t+k} |\mathcal {G}_{t-1} \right] \nonumber \\&\quad + \hat{{\mathcal {P}}}_{i,t+l}^0 ({{\mathcal {H}}}_{i,t+l}^0-\hat{{\mathcal {H}}}_{i,t+l}^0 )\nonumber \\&\quad + \sum _{k=0}^{L-1} \hat{{\mathcal {P}}}_{i,t+l}^0 ({{\mathcal {H}}}_{i,t+l}^{t+k}-\hat{{\mathcal {H}}}_{i,t+l}^{t+k} )\text {E} \left[ \xi _{t+k} |\mathcal {G}_{t-1} \right] \nonumber \\&\quad + \sum _{k=0}^{L-1} \hat{{\mathcal {P}}}_{i,t+l}^{k} ({{\mathcal {H}}}_{i,t+l}^{0}-\hat{{\mathcal {H}}}_{i,t+l}^{0} ) \text {E} \left[ \xi _{t+k} |\mathcal {G}_{t-1} \right] \nonumber \\&\quad + \sum _{m=0}^{L-1} \sum _{k=0}^{L-1} \hat{{\mathcal {P}}}_{i,t+l}^{t+m} ({{\mathcal {H}}}_{i,t+l}^{t+k}-\hat{{\mathcal {H}}}_{i,t+l}^{t+k} ) \text {E} \left[ \xi _{t+m} \xi _{t+k} |\mathcal {G}_{t-1} \right] . \end{aligned}$$

(35)