Coordination of VMI supply chain with replenishment tactic under risk aversion and sales effort

Abstract

This paper considers a vendor-managed inventory (VMI) supply chain consisting of a risk-averse supplier and a risk-neutral retailer engaging in sales promoting efforts. Under the conditional risk at value, we examine three different types of contracts with the replenishment option for coordinating the VMI supply chain, namely, a risk diversification and cost sharing (RDCS) contract, an option and cost sharing contract, and a subsidy and cost sharing contract. Firstly, we derive the optimal production strategy and analyze the capability of each of the proposed contracts in coordinating the VMI supply chain. We find that all of those contracts can achieve coordination of the supply chain with Pareto improvement. Secondly, we also show that both the supplier and the retailer prefer the RDCS contract over the other two contracts. Finally, we use numerical experiments to analyze the impact of risk aversion on contracts’ parameters.

Appendices

Appendices

1.1 A. Proof of Lemma 1

From the definition of CVaR, the supplier’s CVaR performance with wholesale price contract satisfies that

$$\begin{aligned} \varUpsilon (\sigma )= & {} \sigma - \frac{1}{\eta }\int _{Q-e}^\infty (\sigma - \sigma _2 )^ + dF(x) \\&\quad - \frac{1}{\eta }\int _0^{Q-e} (\sigma - \sigma _1 - (w - v - w_1 + c_1 )x)^ + dF(x), \end{aligned}$$

where $\sigma _1 = (v - c)Q + +(w-v)e+(w_1 - c_1 )\mu -e^2$, and $\sigma _2 = (w - c - w_1 + c_1 )Q + (w_1 - c_1 )(e+\mu )-e^2$.

Since $\sigma _1-\sigma _2=-w-v-w_1+c_1)(Q-e)<0$. Thus, we have

$$\begin{aligned} \frac{{\partial \varUpsilon (\sigma )}}{{\partial \sigma }} = \left\{ \begin{array}{ll} 1,&{} \quad \sigma \le \sigma _1, \\ 1 - \frac{1}{\eta }F \left[ \frac{{\sigma - \sigma _1 }}{{w - v - w_1 + c_1 }}\right] ,&{}\quad \sigma _1 \le \sigma < \sigma _2, \\ 1 - \frac{1}{\eta },&{}\quad \sigma > \sigma _2.\\ \end{array} \right. \end{aligned}$$

Obviously, $\varUpsilon (\sigma )$ is left-continuous in $\sigma$ at the point $\sigma =\sigma _2$. And for any $\delta >0$,we have

$$\begin{aligned} |\varUpsilon (\sigma + \delta ) - \varUpsilon (\sigma )|_{\mid {\sigma = \sigma _2 }} = \frac{{\delta (1 - \eta )}}{\eta } \le \frac{\delta }{\eta }. \end{aligned}$$

Thus, $\varUpsilon (\sigma )$ is right-continuous in $\sigma$ at the point $\sigma =\sigma _2$, therefore, $\varUpsilon (\sigma )$ is continuous in $\sigma$ at the point $\sigma =\sigma _2$.

Noting that, it holds $\frac{{\partial \varUpsilon (\sigma )}}{{\partial \sigma }} <0$ for $\sigma >\sigma _2$ and $\frac{{\partial \varUpsilon (\sigma )}}{{\partial \sigma }} >0$ for $\sigma \le \sigma _1$. Thus, for $\sigma _1\le \sigma <\sigma _2$, there exists a point $\sigma _0=(w-v-w_1+c_1)F^{-1}(\eta )+\sigma _1$ such that $\frac{{\partial \varUpsilon (\sigma )}}{{\partial \sigma }}\mid _{\sigma =\sigma _0} =0$ and $Q>F^{-1}(\eta )$. It follows that

$$\begin{aligned} \varUpsilon (\sigma _0 ) = \sigma _1 + \frac{{w - v - w_1 + c_1 }}{\eta }\int _0^{F^{ - 1} (\eta )} x dF(x). \end{aligned}$$

Suppose $\frac{{\partial \varUpsilon (\sigma )}}{{\partial \sigma }}\mid _{\sigma \rightarrow [\sigma _2 ]^ - } = 1 - \frac{1}{\eta }F(Q) \le 0 .$ Due to $\frac{{\partial \varUpsilon (\sigma _0 )}}{{\partial Q}} = v - c < 0$, it holds the optimal order quantity $Q_0^* = F^{ - 1} (\eta )$. However, this is contradictory to $Q>F^{-1}(\eta )$. Hence, it holds $\frac{{\partial \varUpsilon (\sigma )}}{{\partial \sigma }}>0$ for any $\sigma _1\le \sigma <\sigma _2$, and therefore $\sigma _{d}^* = (w - c - w_1 + c_1 )Q + (w_1 - c_1 )(e+\mu )-e^2$.

1.2 B. Proof of the existence and uniqueness of the optimal strategies for $H_{d,i}^s$

We consider the first-order and second-order subdeterminants of $H_{d}^s$ as follows

$$\begin{aligned} \frac{\partial ^2 H_{d}^s}{\partial Q^2}= & {} -\frac{w-v-w_1+c_1}{\eta }f(Q-e)<0,\\ \left| \begin{array}{l@{\quad }l} \frac{\partial ^2 H_{d}^s}{\partial Q^2}&{} \frac{\partial ^2 H_{d}^s}{\partial Q \partial e} \\ \frac{\partial ^2 H_{d}^s}{\partial Q \partial e} &{} \frac{\partial ^2 H_{d}^s}{\partial e^2} \end{array}\right|= & {} \frac{2(w-v-w_1+c_1)}{\eta }f(Q - e) > 0. \end{aligned}$$

According to the definition of the negative definite matrix, the Hessian matrix of $H_{d}^s$ is negative definite with regard to Q and e. Thus, the first-order condition holds. Specifically, the optimal ordering quantity and optimal effort level satisfy Eq. (5).

1.3 C. Proof of Theorem 1

Take the first-order partial derivatives of both the two sides of the first equation of Eq. (5) regarding $\eta$, $w_1$, and $c_1$, respectively. It yields

$$\begin{aligned} \frac{\partial Q_{d}^*}{\partial \eta }= & {} \frac{w-c-w_1+c_1}{f(Q_{d}^*-e_d^*)(w-v-w_1+c_1)}>0,\quad \\ \frac{\partial Q_{d}^*}{\partial w_1}= & {} \frac{-\eta (c-v)}{f(Q_{d}^*-e_d^*)(w-v-w_1+c_1)^2}<0,\\ \frac{\partial Q_{d}^*}{\partial c_1}= & {} \frac{\eta (c-v)}{f(Q_{d}^*-e_d^*)(w-v-w_1+c_1)^2}>0. \end{aligned}$$

1.4 D. Proof of the existence of the supplier’s CVaR utility function with the RDCS contract

According to the description of CVaR, the supplier’s CVaR performance with the RDCS contract satisfies

$$\begin{aligned} H_{a}^s=\sigma -\frac{1}{\eta }\int _0^{Q-e}(\sigma -\sigma _3-\lambda (w-v)x)^+dF(x)-\frac{1}{\eta }\int _{Q-e}^{\infty }(\sigma -\sigma _4)^+dF(x), \end{aligned}$$

where$\sigma _3=[w-c-\lambda (w-v)]Q-\theta e^2+T+\lambda (w-v)e+(w_1-c_1)\mu$, and $\sigma _4=(w-c-w_1+c_1)Q-\theta e^2-T+(w_1-c_1)(e+\mu )$.

The other proof is similar to proof of Lemma 1.

1.5 E. Proof of Theorem 2

Take the first-order partial derivatives of both the two sides of the first equation of Eq. (11) regarding $\eta$, $w_1$, and $c_1$, respectively. It yields

$$\begin{aligned} \frac{\partial Q_{a}^*}{\partial \eta }= & {} \frac{w-c-w_1+c_1}{f(Q_{a}^*-e_a^*)[\lambda (w-v)-w_1+c_1]}>0,\quad \\ \frac{\partial Q_{a}^*}{\partial w_1}= & {} \frac{-\eta [\lambda (w-v)-(w-c)]}{f(Q_{a}^*-e_a^*)[\lambda (w-v)-w_1+c_1]^2}<0,\\ \frac{\partial Q_{a}^*}{\partial c_1}= & {} \frac{\eta [\lambda (w-v)-(w-c)]}{f(Q_{a}^*-e_a^*)[\lambda (w-v)-w_1+c_1]^2}>0. \end{aligned}$$

1.6 F. Proof of Theorem 3

According to the definition of coordination, we let $e_a^*=e_I^*$ and $Q_a^*=Q_I^*$, then we have Eq. (12).

Obviously, $\lambda ^*>\frac{w_1-c_1}{w-v}$ and $\theta _a^*\in (0,1)$. Since $\lambda ^*\le 1$, then $\frac{\eta (w-c-w_1+c_1)(c_1-v)}{(w-v)(c_1-c)} + \frac{w_1 - c_1}{w-v} -1\le 0$, which leads to $\eta \le 1\le \frac{(w-v-w_1+c_1)(c_1-c)}{(w-c-w_1+c_1)(c_1-v)}$.

That is, the supply chain can be coordinated by the RDECS contract for all $\eta \in (0,1]$.

1.7 G. Proof of Theorem 4

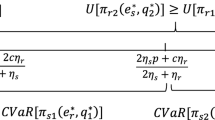
If the RDCS contract achieves the Pareto improvement, then

$$\begin{aligned} H_a^s(Q_I^*,e_I^*)\ge H_d^s(Q_d^*,e_d^*)\; \mathrm{and}\; \pi _a^s(Q_I^*,e_I^*)\ge \pi _d^s(Q_d^*,e_d^*). \end{aligned}$$

Thus, we can obtain $T\in [T_{\min },T_{\max }]$ by solving the previously presented equation set, where $T_{\min }$ and $T_{\max }$ satisfy Eq. (13).

Noting that

$$\begin{aligned}&T_{\max }-T_{\min }\\&\quad =\pi _I(Q_I^*,e_I^*)-\pi _I(Q_d^*,e_d^*)+\frac{(1-\eta )(w-v-w_1+c_1)}{\eta }\int _0^{Q_d^*-e_d^*}F(x)dx\\&\quad \quad +\frac{(1-\eta )(w_1+c_1-\lambda ^*(w-v))}{\eta }\int _0^{Q_I^*-e_I^*}F(x)dx\\&\qquad >\pi _I(Q_I^*,e_I^*)-\pi _I(Q_d^*,e_d^*)+\frac{(1-\eta )(w-v-w_1+c_1)}{\eta }\int _{Q_I^*,e_I^*}^{Q_d^*-e_d^*}F(x)dx. \end{aligned}$$

Thus, only $T_{\max }\ge T_{\min }$ holds, this coordinating contract achieves the Pareto improvement. Therefore, the risk aversion coefficient satisfies that

$$\begin{aligned} \pi _I(Q_I^*,e_I^*)-\pi _I(Q_d^*,e_d^*)+\frac{(1-\eta )(w-v-w_1+c_1)}{\eta }\int _{Q_I^*-e_I^*}^{Q_d^*-e_d^*}F(x)dx>0. \end{aligned}$$

1.8 H. Proof of the existence of the supplier’s CVaR utility function with the OCS contract

According to the description of CVaR, the supplier’s CVaR performance with the OCS contract satisfies

$$\begin{aligned} H_\varepsilon ^s= & {} \sigma -\frac{1}{\eta }\int _0^{Q-e}(\sigma -\sigma _5-(w-v-w_1+c_1)x)^+dF(x)\\&-\frac{1}{\eta }\int _{Q-e}^{\infty }(\sigma -\sigma _6)^+dF(x), \end{aligned}$$

where $\sigma _5=(v-c+k)Q-\theta e^2+(o-v)e+(w_1-c_1)\mu$, and $\sigma _6=(o-c+k-w_1+c_1)Q-\theta e^2+(w_1-c_1)(e+\mu )$.

The other proof is similar to proof of Lemma 1.

1.9 I. Proof of Theorem 5

Take the first-order partial derivatives of both the two sides of the first equation of Eq. (17) regarding $\eta$, $w_1$, and $c_1$, respectively. It yields

$$\begin{aligned} \frac{\partial Q_{\varepsilon }^*}{\partial \eta }= & {} \frac{o-c-w_1+c_1+k}{f(Q_{\varepsilon }^*-e_{\varepsilon }^*)(o-v-w_1+c_1)}>0,\quad \\ \frac{\partial Q_{\varepsilon }^*}{\partial w_1}= & {} \frac{-\eta (c-v-k)}{f(Q_{\varepsilon }^*-e_{\varepsilon }^*)(o-v-w_1+c_1)}<0,\\ \frac{\partial Q_{\varepsilon }^*}{\partial c_1}= & {} \frac{\eta (c-v-k)}{f(Q_{\varepsilon }^*-e_{\varepsilon }^*)(o-v-w_1+c_1)}>0. \end{aligned}$$

1.10 J. Proof of Theorem 6

If the OCS contract can coordinate the supply chain, that is, $e_\varepsilon ^*=e_I^*$ and $Q_\varepsilon ^*=Q_I^*$, then we have

$$\begin{aligned} \left\{ \begin{array}{l} k^*=\frac{(o-v-w_1+c_1)(c_1-c)}{\eta (c_1-v)}-(o-c-w_1+c_1),\\ \theta _\varepsilon ^*=\frac{o-c+k^*}{p-c}. \end{array}\right. \end{aligned}$$

Obviously, $\theta _\varepsilon ^*\in (0,1)$ due to $p-o>k$ and $o-c\ge w_1-c_1$. Note that $c-v>k$ and $p-o>k$, then $\frac{c_1-c}{c_1-v}<\eta \le 1$ for $p-c+v>o$.

If the coordinating OCS contract achieves the Pareto improvement, namely,

$$\begin{aligned} H_\varepsilon ^s(Q_I^*,e_I^*)\ge H_d^s(Q_d^*,e_d^*)\;\mathrm{and} \pi _\varepsilon ^s(Q_I^*,e_I^*)\ge \pi _d^s(Q_d^*,e_d^*). \end{aligned}$$

Then, we can obtain that $o\in [o_{\min },o_{\max }]$, where

$$\begin{aligned} o_{\min }= & {} \frac{\eta [H_d^s(Q_d^*,e_d^*)-H_d^s(Q_I^*,e_I^*)-k^*Q_I^*-(1-\theta _\varepsilon ^*)(e_I^*)^2]}{\eta Q_I^*-E[(Q_I^*-e_I^*-x)^+]}+w,\\ o_{\max }= & {} \frac{\pi _d^r(Q_I^*,e_I^*)-\pi _d^r(Q_d^*,e_d^*)-k^*Q_I^*-(1-\theta _\varepsilon ^*)(e_I^*)^2}{S(Q_I^*,e_I^*)}+w. \end{aligned}$$

Thus, only $o_{\max }\ge o_{\min }$, this coordinating OCS contract has a Pareto improvement, therefore the risk aversion $\eta$ also satisfies that

$$\begin{aligned} \left\{ \begin{array}{l} \pi _I(Q_I^*,e_I^*)-\pi _I(Q_d^*,e_d^*)+\frac{(1-\eta )(w-v-w_1+c_1)}{\eta }\int _{Q_I^*-e_I^*}^{Q_d^*-e_d^*}F(x)dx>0,\\ \eta Q_I^*-\int _0^{Q_I^*-e_I^*}F(x)dx>0.\end{array}\right. \end{aligned}$$

1.11 K. Proof of the existence of the supplier’s CVaR utility function with the SCS contract

According to the description of CVaR, the supplier’s CVaR performance with the SCS contract satisfies

$$\begin{aligned} H_z^s= & {} \sigma -\frac{1}{\eta }\int _0^{Q-e}(\sigma -\sigma _7-(w-v-b-w_1+c_1)x)^+dF(x)\\&-\frac{1}{\eta }\int _{Q-e}^{\infty }(\sigma -\sigma _8)^+dF(x), \end{aligned}$$

where $\sigma _7=(v+b-c)Q-\theta e^2+(w_z-v-b)e+(w_1-c_1)\mu$, and $\sigma _8=(w_z-c-w_1+c_1)Q-\theta e^2+(w_1-c_1)(e+\mu )$.

The other proof is similar to proof of Lemma 1.

1.12 L. Proof of Theorem 7

Take the first-order partial derivatives of both the two sides of the first equation of Eq. (21) regarding $\eta$, $w_1$, and $c_1$, respectively. It yields

$$\begin{aligned} \frac{\partial Q_z^*}{\partial \eta }= & {} \frac{w_z-c-w_1+c_1}{f(Q_z^*-e_z^*)(w_z-v-b-w_1+c_1)}>0,\quad \\ \frac{\partial Q_z^*}{\partial w_1}= & {} \frac{-\eta (c-v-b)}{f(Q_z^*-e_z^*)(w_z-v-b-w_1+c_1)}<0,\\ \frac{\partial Q_z^*}{\partial c_1}= & {} \frac{\eta (c-v-b)}{f(Q_z^*-e_z^*)(w_z-v-b-w_1+c_1)}>0. \end{aligned}$$

1.13 M. Proof of Theorem 8

If the SCS contract can coordinate the supply chain, that is, $e_z^*=e_I^*$ and $Q_z^*=Q_I^*$, then we have

$$\begin{aligned} \left\{ \begin{array}{l} b^*=w_z-v-w_1+c_1-\frac{\eta (w_z-c-w_1+c_1)(c_1-v)}{c_1-c},\\ \theta _z^*=\frac{w_z-c}{p-c}. \end{array}\right. \end{aligned}$$

Obviously, $\theta _z^*\in (0,1)$ due to $p>w>c$. Note that $w_z-v>b^*>0$, then $\eta \le 1$.

If the coordinating SCS contract achieves the Pareto improvement, namely,

$$\begin{aligned} H_z^s(Q_I^*,e_I^*)\ge H_d^s(Q_d^*,e_d^*)\;\mathrm{and}\; \pi _z^s(Q_I^*,e_I^*)\ge \pi _d^s(Q_d^*,e_d^*). \end{aligned}$$

Then, we can obtain that $w_z\in [w_{z,\min },w_{z,\max }]$, where

$$\begin{aligned} w_{z,\min }= & {} \frac{\eta [H_d^s(Q_d^*,e_d^*)-H_d^s(Q_I^*,e_I^*)-(1-\theta _z^*)(e_I^*)^2]-b^*E[(Q_I^*-e_I^*-x)^+]}{\eta Q_I^*-E[(Q_I^*-e_I^*-x)^+]}\\&+w,\\ w_{z,\max }= & {} \frac{\pi _d^r(Q_I^*,e_I^*)-\pi _d^r(Q_d^*,e_d^*)-(1-\theta _z^*)(e_I^*)^2-b^*E[(Q_I^*-e_I^*-x)^+]}{S(Q_I^*,e_I^*)}+w. \end{aligned}$$

Thus, only $w_{z,\max }\ge w_{z,\min }$, this coordinating SCS contract has a Pareto improvement, therefore the risk aversion $\eta$ also satisfies that

$$\begin{aligned} \left\{ \begin{array}{l} \pi _I(Q_I^*,e_I^*)-\pi _I(Q_d^*,e_d^*)+\frac{(1-\eta )(w-v-w_1+c_1)}{\eta }\int _{Q_I^*-e_I^*}^{Q_d^*-e_d^*}F(x)dx>0,\\ \eta Q_I^*-\int _0^{Q_I^*-e_I^*}F(x)dx>0.\end{array}\right. \end{aligned}$$

1.14 N. Proof of Theorem 9

First, we compare the OCS contract with the RDCS contract by setting the following equations

$$\begin{aligned} T_1&=(\theta _\varepsilon ^*-\theta _a^*)(e_I^*)^2-k^*Q_I^*+(w-o)S(Q_I^*,e_I^*)\\&\quad +(1-\lambda ^*)(w-v)\int _0^{Q_I^*-e_I^*}F(x)dx,\\ T_2&=(\theta _\varepsilon ^*-\theta _a^*)(e_I^*)^2-k^*Q_I^*+(w-o)Q_I^*\\&\quad +\frac{o-v-\lambda ^*(w-v)}{\eta }\int _0^{Q_I^*-e_I^*}F(x)dx. \end{aligned}$$

Then, combing with $o\in [o_{\min },o_{\max }]$, we have

$$\begin{aligned} T_2-T_1= & {} \frac{(1-\eta )[o-v-\lambda ^*(w-v]}{\eta }\int _0^{Q_I^*-e_I^*}F(x)dx>0.\\ T_1-T_{\min }= & {} (o_{\max }-o)S(Q_I^*,e_I^*)\ge 0.\\ T_{\max }-T_2= & {} (o-o_{\min })(Q_I^*-\frac{1}{\eta }\int _0^{Q_I^*-e_I^*}F(x)dx)\ge 0. \end{aligned}$$

Thus, the following results hold. In the interval $[T_1,T_2]$, it holds that $H_a^s\ge H_\varepsilon ^s$ and $\pi _a^r\ge \pi _\varepsilon ^r$. However, $H_a^s>H_\varepsilon ^s$ and $\pi _a^r<\pi _\varepsilon ^r$ if $T<T_1$; $H_a^s<H_\varepsilon ^s$ and $\pi _a^r>\pi _\varepsilon ^r$ if $T>T_2$. Thus, only in interval $[T_1,T_2]$, both firms can earn a higher performance with a same contract between the OCS contract and the RDCS contract, i.e., both firms would adopt a same contract, namely the RDCS contract, only if $T\in [T_1,T_2]$.

Second, we compare the SCS contract with the RDCS contract by setting the following expressions

$$\begin{aligned} T_3&=(\theta _z^*-\theta _a^*)(e_I^*)^2+(w-w_z)S(Q_I^*,e_I^*)\\&\quad +([1-\lambda ^*)(w-v)-b^*]\int _0^{Q_I^*-e_I^*}F(x)dx,\\ T_4&=(\theta _z^*-\theta _a^*)(e_I^*)^2+(w-w_z)Q_I^*\\&\quad +\frac{w_z-v-b^*-\lambda ^*(w-v)}{\eta }\int _0^{Q_I^*-e_I^*}F(x)dx. \end{aligned}$$

Then, combing with $w_z\in [w_{z,\min },w_{z,\max }]$, we have

$$\begin{aligned} T_4-T_3&=\frac{(1-\eta )[w_z-v-b^*-\lambda ^*(w-v]}{\eta }\int _0^{Q_I^*-e_I^*}F(x)dx>0.\\ T_3-T_{\min }&=(w_{z,\max }-w_z)S(Q_I^*,e_I^*)\ge 0.\\ T_{\max }-T_4&=(w_z-w_{z,\min })(Q_I^*-\frac{1}{\eta }\int _0^{Q_I^*-e_I^*}F(x)dx)\ge 0. \end{aligned}$$

Thus, the following results hold. In the interval $[T_3,T_4]$, it holds that $H_a^s\ge H_z^s$ and $\pi _a^r\ge \pi _z^r$. However, $H_a^s>H_z^s$ and $\pi _a^r<\pi _z^r$ if $T<T_3$; $H_a^s<H_z^s$ and $\pi _a^r>\pi _z^r$ if $T>T_4$. Thus, only in interval $[T_3,T_4]$, both firms can earn a higher performance with a same contract between the SCS contract and the RDCS contract, i.e., both firms would adopt a same contract, namely the RDCS contract, only if $T\in [T_3,T_4]$.