Skip to main content
SpringerLink
Log in

Convergence analysis of the Adini element on a Shishkin mesh for a singularly perturbed fourth-order problem in two dimensions

  • Published:
Advances in Computational Mathematics Aims and scope Submit manuscript

Abstract

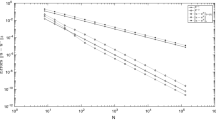
We consider the singularly perturbed fourth-order boundary value problem ε2Δ2u −Δu = f on the unit square \({\Omega }\subset \mathbb {R}^{2}\), with boundary conditions u = ∂u/∂n = 0 on ∂Ω. Here, ε ∈ (0,1) is a small parameter. The problem is solved numerically by means of Adini finite elements—a simple nonconforming finite element method for this problem. Under reasonable assumptions on the structure of the boundary layers that appear in the solution, a family of suitable Shishkin meshes with N2 elements is constructed and convergence of the method is proved in a ‘broken’ version of the Sobolev norm \(v\mapsto \left (\varepsilon ^{2}|v|_{2}^{2} + |v|_{1}^{2} \right )^{1/2}\). For a particular choice of the mesh, the error in the computed solution is at most C [ε1/2(N− 1 lnN)2 + min {ε1/2,ε− 3/2N− 2} + N− 3], where the constant C is independent of ε and N. Numerical results support our theoretical convergence rates, even for an example where not all the hypotheses of our theory are satisfied.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Andreev, V. B.: On the accuracy of grid approximations of nonsmooth solutions of a singularly perturbed reaction-diffusion equation in the square. Differ. Uravn. 42 (7), 895–906, 1005 (2006). https://doi.org/10.1134/S0012266106070044

    MathSciNet  Google Scholar 

  2. Brenner, S. C., Gudi, T., Neilan, M., Sung, L.Y.: c 0 penalty methods for the fully nonlinear Monge-Ampère equation. Math. Comput. 80 (276), 1979–1995 (2011). https://doi.org/10.1090/S0025-5718-2011-02487-7 https://doi.org/10.1090/S0025-5718-2011-02487-7

    Article  MATH  Google Scholar 

  3. Brenner, S. C., Neilan, M.: A c 0 interior penalty method for a fourth order elliptic singular perturbation problem. SIAM J. Numer. Anal. 49(2), 869–892 (2011). https://doi.org/10.1137/100786988

    Article  MathSciNet  MATH  Google Scholar 

  4. Brenner, S. C., Scott, L. R.: The Mathematical Theory of Finite Element Methods Texts in Applied Mathematics, 3rd edn., vol. 15. Springer, New York (2008). https://doi.org/10.1007/978-0-387-75934-0

  5. Chen, H., Chen, S.: Uniformly convergent nonconforming element for 3-D fourth order elliptic singular perturbation problem. J. Comput. Math. 32(6), 687–695 (2014). https://doi.org/10.4208/jcm.1405-m4303 https://doi.org/10.4208/jcm.1405-m4303

    Article  MathSciNet  MATH  Google Scholar 

  6. Chen, H., Chen, S., Xiao, L.: Uniformly convergent c 0-nonconforming triangular prism element for fourth-order elliptic singular perturbation problem. Numer. Methods Partial Differential Equations 30 (6), 1785–1796 (2014). https://doi.org/10.1002/num.21878

    Article  MathSciNet  MATH  Google Scholar 

  7. Chen, S., Zhao, Y., Shi, D.: Anisotropic interpolations with application to nonconforming elements. Appl. Numer. Math. 49(2), 135–152 (2004). https://doi.org/10.1016/j.apnum.2003.07.005

    Article  MathSciNet  MATH  Google Scholar 

  8. Chen, S.C., Zhao, Y.C., Shi, D.Y.: Non c 0 nonconforming elements for elliptic fourth order singular perturbation problem. J. Comput. Math. 23(2), 185–198 (2005)

    MathSciNet  MATH  Google Scholar 

  9. Ciarlet, P. G.: The Finite Element Method for Elliptic Problems. North-Holland Publishing Company, Amsterdam (1978)

    MATH  Google Scholar 

  10. Constantinou, P., Varnava, C., Xenophontos, C.: An hp finite element method for 4th order singularly perturbed problems. Numer. Algorithms 73(2), 567–590 (2016). https://doi.org/10.1007/s11075-016-0108-9 https://doi.org/10.1007/s11075-016-0108-9

    Article  MathSciNet  MATH  Google Scholar 

  11. Constantinou, P., Xenophontos, C.: An hp finite element method for a 4th order singularly perturbed boundary value problem in two dimensions. Computers and Mathematics with Applications. https://doi.org/10.1016/j.camwa.2017.02.009. http://www.sciencedirect.com/science/article/pii/S0898122117300755 (2017)

  12. Du, S., Lin, R., Zhang, Z.: Robust residual-based a posteriori error estimators for mixed finite element methods for fourth order elliptic singularly perturbed problems. arXiv:http://arXiv.org/abs/1609.04506 (2016)

  13. Farrell, P. A., Hegarty, A. F., Miller, J. J. H., O’Riordan, E., Shishkin, G. I.: Robust Computational Techniques for Boundary Layers Applied Mathematics (Boca Raton), vol. 16. Chapman & Hall/CRC, Boca Raton (2000)

    Book  Google Scholar 

  14. Franz, S., Roos, H. G.: Robust error estimation in energy and balanced norms for singularly perturbed fourth order problems. Comput. Math. Appl. 72 (1), 233–247 (2016). https://doi.org/10.1016/j.camwa.2016.05.001 https://doi.org/10.1016/j.camwa.2016.05.001

    Article  MathSciNet  Google Scholar 

  15. Franz, S., Roos, H. G., Wachtel, A.: A c 0 interior penalty method for a singularly-perturbed fourth-order elliptic problem on a layer-adapted mesh. Numer. Methods Partial Differential Equations 30(3), 838–861 (2014). https://doi.org/10.1002/num.21839

    Article  MathSciNet  MATH  Google Scholar 

  16. Ganesan, S., Tobiska, L.: Finite Elements: Theory and Algorithms. IISc. Cambridge University Press, Cambridge (2017)

    Book  MATH  Google Scholar 

  17. Guzmán, J., Leykekhman, D., Neilan, M.: A family of non-conforming elements and the analysis of Nitsche’s method for a singularly perturbed fourth order problem. Calcolo 49(2), 95–125 (2012). https://doi.org/10.1007/s10092-011-0047-8

    Article  MathSciNet  MATH  Google Scholar 

  18. Hu, J., Huang, Y.: The correction operator for the canonical interpolation operator of the Adini element and the lower bounds of eigenvalues. Sci. China Math. 55(1), 187–196 (2012). https://doi.org/10.1007/s11425-011-4267-9

    Article  MathSciNet  MATH  Google Scholar 

  19. Hu, J., Shi, Z.: A lower bound of the l 2 norm error estimate for the Adini element of the biharmonic equation. SIAM J. Numer. Anal. 51(5), 2651–2659 (2013). https://doi.org/10.1137/130907136

    Article  MathSciNet  MATH  Google Scholar 

  20. Hu, J., Yang, X., Zhang, S.: Capacity of the Adini element for biharmonic equations. J. Sci. Comput. 69(3), 1366–1383 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  21. Lascaux, P., Lesaint, P.: Some nonconforming finite elements for the plate bending problem. Rev. Franç,aise Automat. Informat. Recherche Operationnelle Sér. Rouge Anal. Numér. 9(R-1), 9–53 (1975)

    MathSciNet  MATH  Google Scholar 

  22. Luo, P., Lin, Q.: High accuracy analysis of the Adini’s nonconforming element. Computing 68(1), 65–79 (2002). https://doi.org/10.1007/s006070200003

    Article  MathSciNet  MATH  Google Scholar 

  23. Mao, S., Chen, S.: Accuracy analysis of Adini’s non-conforming plate element on anisotropic meshes. Comm. Numer. Methods Engrg. 22(5), 433–440 (2006). https://doi.org/10.1002/cnm.825

    Article  MathSciNet  MATH  Google Scholar 

  24. Nilssen, T. K., Tai, X. C., Winther, R.: A robust nonconforming h 2-element. Math. Comp. 70 (234), 489–505 (2001). https://doi.org/10.1090/S0025-5718-00-01230-8

    Article  MathSciNet  MATH  Google Scholar 

  25. O’Malley, R.E., Jr.: Introduction to singular perturbations. Academic Press [A subsidiary of Harcourt Brace Jovanovich, Publishers], New York-London. Applied Mathematics and Mechanics, vol. 14 (1974)

  26. Panaseti, P., Zouvani, A., Madden, N., Xenophontos, C.: A c 1-conforming hp finite element method for fourth order singularly perturbed boundary value problems. Appl. Numer. Math. 104, 81–97 (2016). https://doi.org/10.1016/j.apnum.2016.02.002

    Article  MathSciNet  MATH  Google Scholar 

  27. Roos, H. G., Stynes, M., Tobiska, L.: Robust Numerical Methods for Singularly Perturbed differential Equations, Springer Series in Computational Mathematics, 2nd edn., vol. 24. Springer, Berlin (2008). Convection-diffusion-reaction and flow problems

  28. Semper, B.: Conforming finite element approximations for a fourth-order singular perturbation problem. SIAM J. Numer. Anal. 29(4), 1043–1058 (1992). https://doi.org/10.1137/0729063

    Article  MathSciNet  MATH  Google Scholar 

  29. Shi, Z. C., Wang, M.: Finite Element Method. Science Press, Beijing (2013)

    Google Scholar 

  30. Wang, L., Wu, Y., Xie, X.: Uniformly stable rectangular elements for fourth order elliptic singular perturbation problems. Numer. Methods Partial Differential Equations 29(3), 721–737 (2013). https://doi.org/10.1002/num.21723

    Article  MathSciNet  MATH  Google Scholar 

  31. Wang, M., Meng, X.: A robust finite element method for a 3-D elliptic singular perturbation problem. J. Comput. Math. 25(6), 631–644 (2007)

    MathSciNet  MATH  Google Scholar 

  32. Wang, M., Shi, Z. C., Xu, J.: Some n-rectangle nonconforming elements for fourth order elliptic equations. J. Comput. Math. 25(4), 408–420 (2007)

    MathSciNet  MATH  Google Scholar 

  33. Wang, M., Xu, J.C., Hu, Y.C.: Modified M,orley element method for a fourth order elliptic singular perturbation problem. J. Comput. Math. 24(2), 113–120 (2006)

    MathSciNet  Google Scholar 

  34. Wang, W., Huang, X., Tang, K., Zhou, R.: Morley-Wang-Xu element methods with penalty for a fourth order elliptic singular perturbation problem. Adv. Comput. Math. https://doi.org/10.1007/s10444-017-9572-6 https://doi.org/10.1007/s10444-017-9572-6 (2017)

  35. Xie, P., Shi, D., Li, H.: A new robust c 0-type nonconforming triangular element for singular perturbation problems. Appl. Math. Comput. 217(8), 3832–3843 (2010). https://doi.org/10.1016/j.amc.2010.09.042 https://doi.org/10.1016/j.amc.2010.09.042

    MathSciNet  MATH  Google Scholar 

  36. Yang, Y., Zhang, Z., Lin, F.: Eigenvalue approximation from below using non-conforming finite elements. Sci. China Math. 53(1), 137–150 (2010). https://doi.org/10.1007/s11425-009-0198-0

    Article  MathSciNet  MATH  Google Scholar 

  37. Zhang, S., Wang, M.: A posteriori estimator of nonconforming finite element method for fourth order elliptic perturbation problems. J. Comput. Math. 26(4), 554–577 (2008)

    MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

We thank two unknown reviewers for their extremely careful reading of our manuscript and for giving us many helpful suggestions.

Funding

The research of the second author is supported in part by the National Natural Science Foundation of China under grants 91430216 and NSAF U1530401.

Author information

Authors and Affiliations

  1. Division of Applied and Computational Mathematics, Beijing Computational Science Research Center, Beijing, China

    Xiangyun Meng & Martin Stynes

Authors
  1. Xiangyun Meng
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Martin Stynes
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Martin Stynes.

Additional information

Communicated by: Long Chen

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Meng, X., Stynes, M. Convergence analysis of the Adini element on a Shishkin mesh for a singularly perturbed fourth-order problem in two dimensions. Adv Comput Math 45, 1105–1128 (2019). https://doi.org/10.1007/s10444-018-9646-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10444-018-9646-0

Keywords

Mathematics Subject Classification (2010)

Search

Navigation