Impact of supply risks on procurement decisions

Abstract

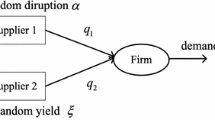
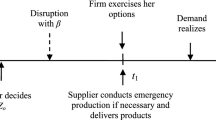
We consider a firm that procures a product from a regular supplier whose production is subject to both supply disruption and random yield risks and a backup supplier whose production capacity requires reservation in advance. Under both deterministic and stochastic demand, we study the impact of the two types of supply risks on the firm’s optimal procurement decisions and the importance of correctly identifying the source of supply risks. We find that if the overall supply risk is unchanged but its main source shifts from random yield to supply disruption, the firm should order more from the regular supplier and reserve less capacity from the backup supplier. Ignoring the existence of supply disruption leads to under-utilization of the regular supplier and over-utilization of the backup supplier. Moreover, we examine the option value of the reserved capacity that is affected by the uncertainty of customer demand. We find that the option value increases/decreases in demand uncertainty if the reservation capacity is exercised after/before demand is realized.

Appendix

1.1 A.1 Proof of propositions

Proof of Proposition 1

Notice that if x _r =0, by (8), we have the profit function $\pi(0,x_{k})=\lim_{x_{r}\rightarrow 0}\pi(x_{r},x_{k})=(p-c_{e})x_{k}-l(d-x_{k})-c_{k}x_{k}=(p+l-c_{e}-c_{k})x_{k}-ld$, where x _k ∈[0,d]. Hence, $x_{k}^{*}(0)=d$ if p+l>c _e +c _k ; otherwise, $x_{k}^{*}(0)=0$. If x _r >0, then we have

$$\begin{aligned} \pi(x_r,x_k) =&(p-s)d+\bigl[(p+l-c_e)x_k-(p+l-s)d \bigr]q+s(1-q)x_rE[\xi_r] \\ &{}+s(1-q)x_r\int_0^{\frac{d}{x_r}}G(\xi)d \xi \\ &{} -c_e(1-q)x_r\int_{\frac{d-x_k}{x_r}}^{\frac{d}{x_r}}G( \xi)d\xi-(l+p) (1-q)x_r\int_0^{\frac{d-x_k}{x_r}}G( \xi)d\xi \\ &{} -\bigl(\lambda+(1-\lambda) (1-q)E[\xi_r]\bigr)c_rx_r-c_kx_k, \end{aligned}$$

(12)

where the last equality follows from $F(x\mid x_{r})=q+(1-q)G(\frac{x}{x_{r}})$ and integration by parts. Thus,

$$ \frac{\partial \pi(x_r,x_k)}{\partial x_k}=(l+p-c_e)q-c_k+(l+p-c_e) (1-q)G\biggl(\frac{d-x_k}{x_r}\biggr). $$

(13)

Since l+p>c _e , π(x _r ,x _k ) is concave in x _k . Also note that $\frac{\partial \pi(x_{r},x_{k})}{\partial x_{k}}$ is decreasing in x _r , but increasing in q. If G ₁≤ _st G ₂, then G ₁(ξ)≥G ₂(ξ), where ξ≥0. Hence, $\frac{\partial \pi(x_{r},x_{k})}{\partial x_{k}}$ is decreasing in G. By Theorem 2.8.2 of Topkis (1998), the claims hold. □

Proof of Proposition 2

By (13) we have $\frac{\partial^{2} \pi(x_{r},x_{k})}{\partial x_{k}\partial x_{r}}\leq 0$. This implies that π(x _r ,x _k ) is submodular in (x _r ,x _k ). Notice that $\frac{\partial \pi(x_{r},x_{k})}{\partial x_{k}}$ is increasing in q. By (12), we have

$$\begin{aligned} \frac{\partial\pi(x_k,x_r)}{\partial x_r} =& s(1-q)E[\xi_r]-\bigl(\lambda+(1-\lambda) (1-q)E[\xi_r]\bigr)c_r \\ &{}+s(1-q) \int_0^{\frac{d}{x_r}}G(\xi)d\xi -c_e(1-q)\int_{\frac{d-x_k}{x_r}}^{\frac{d}{x_r}}G(\xi)d\xi \\ &{}-(l+p) (1-q)\int_0^{\frac{d-x_k}{x_r}}G(\xi)d\xi -(s-c_e) (1-q)\frac{d}{x_r}G\biggl(\frac{d}{x_r}\biggr) \\ &{}+(l+p-c_e) (1-q)\frac{d-x_k}{x_r}G\biggl(\frac{d-x_k}{x_r} \biggr) \\ =& s(1-q)E[\xi_r]-\bigl(\lambda+(1-\lambda) (1-q)E[ \xi_r]\bigr)c_r \\ &{}+(c_e-s) (1-q)\int_0^{\frac{d}{x_r}}\xi g(\xi)d\xi \\ &{}+(l+p-c_e) (1-q)\int_0^{\frac{d-x_k}{x_r}}\xi g(\xi)d\xi. \end{aligned}$$

Hence, $\frac{\partial \pi(x_{r},x_{k})}{\partial x_{r}}$ is decreasing in q. By Theorem 2.8.2 of Topkis (1998), the claim holds. □

Proof of Proposition 3

Given deterministic demand d, the optimal decision must satisfies: $x_{r}^{\ast }\in [ 0,\frac{d}{\delta } ]$, $x_{k}^{\ast }\in [ 0,d ]$, and $x_{r}^{\ast }+x_{k}^{\ast }\geq d$. The firm’s expected profit is

$$\begin{aligned} \pi ( x_{r},x_{k} ) =&q \bigl[ ( p-c_{e} ) x_{k}-l ( d-x_{k} ) \bigr] \\ &{}+ ( 1-q ) q_{r} \bigl[ p\min ( d,\delta x_{r}+x_{k} ) -c_{e}\min ( d-\delta x_{r},x_{k} ) -l ( d- \delta x_{r}-x_{k} ) ^{+} \bigr] \notag \\ &{}+ ( 1-q ) ( 1-q_{r} ) \bigl[ pd-c_{e} ( d-x_{r} ) ^{+}+s ( x_{r}-d ) ^{+} \bigr] \notag \\ &{}- \bigl( \lambda + ( 1-\lambda ) ( 1-q ) E [ \xi _{r} ] \bigr) c_{r}x_{r}-c_{k}x_{k}. \end{aligned}$$

(14)

For given x _r ,

$$ \frac{\partial \pi ( x_{r},x_{k} ) }{\partial x_{k}}=-c_{k}+q ( p+l-c_{e} ) +\left \{ \begin{array}{l} 0,\quad \text{if } x_{k}\geq d-\delta x_{r}, \\ ( 1-q ) q_{r} ( p+l-c_{e} ),\quad \text{if } x_{k}<d-\delta. x_{r} \end{array} \right . $$

Since p+l−c _e >0, $\frac{\partial \pi ( x_{r},x_{k} ) }{\partial x_{k}}$ is decreasing in x _k . If (q+(1−q)q _r )(p+l−c _e )<c _k , then $x_{k}^{\ast } ( x_{r} ) =0$. Else if (q+(1−q)q _r )(p+l−c _e )≥c _k ≥q(p+l−c _e ), then $x_{k}^{\ast } ( x_{r} ) =d-\delta x_{r}$. Else, c _k <q(p+l−c _e ) and $x_{k}^{\ast } ( x_{r} ) =d$. This completes the proof of Claim (1).

For c _k ∈[q(p+l−c _e ),(q+(1−q)q _r )(p+l−c _e )], since $x_{k}^{\ast } ( x_{r} ) =d-\delta x_{r}$, the expected profit in (14) can be rewritten as

$$\begin{aligned} \pi \bigl( x_{r},x_{k}^{\ast } ( x_{r} ) \bigr) =&q \bigl[ ( p+l-c_{e} ) ( d-\delta x_{r} ) -ld \bigr] + ( 1-q ) q_{r} \bigl[ pd-c_{e} ( d-\delta x_{r} ) \bigr] \\ &{}+ ( 1-q ) ( 1-q_{r} ) \bigl[ pd-c_{e} ( d-x_{r} ) ^{+}+s ( x_{r}-d ) ^{+} \bigr] \\ &{}- \bigl( \lambda + ( 1-\lambda ) ( 1-q ) E [ \xi _{r} ] \bigr) c_{r}x_{r}-c_{k} ( d-\delta x_{r} ), \end{aligned}$$

which is a piecewise linear function of x _r . Since

$$\begin{aligned} \frac{d\pi ( x_{r},x_{k}^{\ast } ( x_{r} ) ) }{dx_{r}} =&-q\delta ( p+l-c_{e} ) + ( 1-q ) q_{r}c_{e}\delta + ( 1-q ) ( 1-q_{r} ) [ c_{e}1_{x_{r}<d}+s1_{x_{r}>d} ] \\ &{}- \bigl( \lambda + ( 1-\lambda ) ( 1-q ) E [ \xi _{r} ] \bigr) c_{r}+c_{k}\delta, \end{aligned}$$

$x_{r}^{\ast }\in \{ 0,d,\frac{d}{\delta } \}$. By $x_{k}^{\ast } ( x_{r} ) =d-\delta x_{r}$ we have $( x_{r}^{\ast },x_{k}^{\ast } ) \in \{ ( 0,d ) , ( d, ( 1-\delta ) d ) , ( \frac{d}{\delta },0 ) \}$. This completes the proof of Claim (2).

When $( x_{r}^{\ast },x_{k}^{\ast } ) = ( d, ( 1-\delta ) d )$, here we show $x_{k}^{\ast }$ is decreasing in q within set $A_{\mu ,\sigma ^{2}}$ by showing δ(q) is increasing in q. According to the definition of $A_{\mu,\sigma^{2}}$ in (10), any given risk type (q,δ(q),q _r (q)) within set $A_{\mu ,\sigma ^{2}}$ satisfies $\delta(q)= \frac{\mu(1-\mu)-\sigma^{2}}{1-\mu-q}$ and q _r (q)= $\frac{1-\mu -q}{ ( 1-q ) ( 1-\delta ) }$. By some algebra, we have

$$ \sigma ^{2}+\mu ^{2}=- ( \delta +1 ) ( 1-\mu -q ) + ( 1-q ). $$

(15)

Thus, in order to keep q _r >0 we need q<1−μ. By the implicit function theorem and (15) we have $\frac{d\delta }{dq}=\frac{\delta }{1-\mu -q}$. Thus, $\frac{d\delta }{dq}>0$. This completes the proof of Claim (3). □

Proof of Proposition 4

When $x_{r}^{\ast }>0$ and $x_{k}^{*}\in(0,d)$ the optimal solution $( x_{r}^{\ast },x_{k}^{\ast } )$ is obtained by solving a first order condition J(x _r )=0 and $x_{k}^{\ast }=d-y^{\ast }x_{r}^{\ast }$, where $y^{*}=G^{-1}(1-\frac{l+p-c_{e}-c_{k}}{(l+p-c_{e})(1-q)})$ (see Sect. A.2 for details of J(x _r ) and the procedure of solving for the optimal solution). With random yield that follows uniform distribution on [γ−δ,γ+δ], we have $y^{\ast }=2\delta ( 1-\frac{l+p-c_{e}-c_{k}}{ ( l+p-c_{e} ) ( 1-q ) } ) + ( \gamma -\delta )$, and

$$\begin{aligned} J ( x_{r} ) =&c ( q,G ) + ( l+p-c_{e} ) ( 1-q ) \int _{0}^{y^{\ast }}\frac{\xi }{2\delta }d\xi + ( c_{e}-s ) ( 1-q ) \int_{0}^{\frac{d}{x_{r}}} \frac{\xi}{2\delta }d\xi \notag \\ =&c ( q,G ) +\frac{ ( l+p-c_{e} ) ( 1-q ) ( y^{\ast } ) ^{2}+ ( c_{e}-s ) ( 1-q ) ( \frac{d}{x_{r}} ) ^{2}}{4\delta }. \end{aligned}$$

(16)

First, we show $\frac{dx_{r}^{\ast } ( q ) }{dq}>0$. The first term in (16), c(q,G), is defined as c(q,G)=s(1−q)E[ξ _r ]−(λ+(1−λ)(1−q)E[ξ _r ])c _r . Since $E [ \xi _{r} ] =\gamma ( q ) =\frac{\mu }{1-q}$, c(q,G)=sμ−(λ+(1−λ)μ)c _r . Thus, within set $A_{\mu ,\sigma ^{2}}$, c(q,G) is independent of q for all λ∈[0,1]. Based on (16), $J ( x_{r}^{\ast } ( q ) ) =0$, and the implicit function theorem, we have

$$\begin{aligned} &-\frac{ ( l+p-c_{e} ) ( 1-q ) ( y^{\ast } ) ^{2}+ ( c_{e}-s ) ( 1-q ) ( \frac{d}{x_{r}^{\ast } ( q ) } ) ^{2}}{4\delta ^{2}}\frac{d\delta }{dq} \\ &\qquad{}+\frac{1}{4\delta } \biggl[- ( l+p-c_{e} ) \bigl( y^{\ast } \bigr) ^{2}+2 ( l+p-c_{e} ) ( 1-q ) y^{\ast }\frac{dy^{\ast } ( q ) }{dq} \\ &\qquad{}- ( c_{e}-s ) \biggl( \frac{d}{x_{r}^{\ast } ( q ) } \biggr) ^{2}-2\frac{ ( c_{e}-s ) ( 1-q ) d^{2}}{x_{r}^{\ast } ( q ) ^{3}}\frac{dx_{r}^{\ast } ( q ) }{dq} \biggr] \\ &\quad{}=0 \end{aligned}$$

By some algebra, we have

$$\begin{aligned} &2\delta \frac{ ( c_{e}-s ) ( 1-q ) d^{2}}{x_{r}^{\ast } ( q ) ^{3}}\frac{dx_{r}^{\ast } ( q ) }{dq} \\ &\quad{}=2\delta ( l+p-c_{e} ) ( 1-q ) y^{\ast } \frac{dy^{\ast } ( q ) }{dq}- ( l+p-c_{e} ) \bigl( y^{\ast } \bigr) ^{2} \biggl( \delta + ( 1-q ) \frac{d\delta }{dq} \biggr) \\ &\qquad{}- ( c_{e}-s ) \biggl( \delta + ( 1-q ) \frac{d\delta }{dq} \biggr) \frac{d^{2}}{x_{r}^{\ast } ( q ) ^{2}}. \end{aligned}$$

Since c _e >s and δ>0, the necessary and sufficient condition for $\frac{dx_{r}^{\ast} ( q ) }{dq}>0$ is

$$\begin{aligned} &2\delta ( l+p-c_{e} ) ( 1-q ) y^{\ast }\frac{dy^{\ast } ( q ) }{dq} \\ &\quad{}-\biggl[ ( l+p-c_{e} ) \bigl( y^{\ast } \bigr) ^{2}+ ( c_{e}-s )\frac{d^{2}}{x_{r}^{\ast } ( q ) ^{2}}\biggr] \biggl( \delta+ ( 1-q ) \frac{d\delta }{dq} \biggr)>0. \end{aligned}$$

(17)

Now we show: if $1/2<v<\frac{\mu }{2\sqrt{3}\sigma }$, then there exists $\hat{q}\in [ 0,1 ]$ such that for $q\in ( 0,\hat{q} )$ inequality (17) holds and $\frac{dx_{r}^{\ast } ( q ) }{dq}>0$. More specifically, we show: (a) $\delta + ( 1-q ) \frac{d\delta }{dq}<0$, (b) $\frac{dy^{\ast } ( q ) }{dq}>0$. Since l+p−c _e >0 and c _e −s>0, Claims (a) and (b) imply that each of the terms in the left-hand side of inequality (17) is positive, and therefore the inequality holds and $\frac{dx_{r}^{\ast } ( q ) }{dq}>0$.

Proof of (a) By definition of δ(q), we have

$$\begin{aligned} \frac{d\delta ( q ) }{dq} =&\frac{\sqrt{3}\sigma }{ ( 1-q ) ^{2}}\sqrt{1-q \biggl( 1+\frac{\mu ^{2}}{\sigma ^{2}} \biggr) }-\frac{\sqrt{3}\sigma }{2 ( 1-q ) }\frac{1+\frac{\mu ^{2}}{\sigma ^{2}}}{\sqrt{1-q ( 1+\frac{\mu ^{2}}{\sigma ^{2}} ) }} \notag \\ =&\sqrt{3}\sigma \frac{2- ( q+1 ) ( 1+\frac{\mu ^{2}}{\sigma ^{2}} ) }{2 ( 1-q ) ^{2}\sqrt{1-q ( 1+\frac{\mu ^{2}}{\sigma ^{2}} ) }}\notag \\ \overbrace{=}^{\text{By definition of }\delta }&3\sigma ^{2}\frac{2- ( q+1 ) ( 1+\frac{\mu ^{2}}{\sigma ^{2}} ) }{2 ( 1-q ) ^{3}\delta }. \end{aligned}$$

(18)

By some algebra, we have

$$ \delta + ( 1-q ) \frac{d\delta }{dq}=\sqrt{3}\sigma \frac{4- ( 3q+1 ) ( 1+\frac{\mu ^{2}}{\sigma ^{2}} ) }{2 ( 1-q ) \sqrt{1-q ( 1+\frac{\mu ^{2}}{\sigma ^{2}} ) }}. $$

Thus, $\delta + ( 1-q ) \frac{d\delta }{dq}<0$ if and only if $( 3q+1 ) ( 1+\frac{\mu ^{2}}{\sigma ^{2}} ) >4$, which is true since $\mu >\sqrt{3}\sigma$ and 3q+1>1.

Proof of (b) By the definition of γ(q), we have

$$ \frac{d\gamma ( q ) }{dq}=\frac{\mu }{ ( 1-q ) ^{2}}>0. $$

(19)

According to the definition of y ^∗ and v,

$$ y^{\ast }=2\delta \biggl( 1-\frac{v}{1-q} \biggr) + ( \gamma -\delta ) =\delta \biggl( 1-\frac{2v}{1-q} \biggr) +\gamma. $$

Thus,

$$\begin{aligned} \frac{dy^{\ast } ( q ) }{dq} =&\frac{d\delta }{dq} \biggl( 1-\frac{2v}{ ( 1-q ) } \biggr) - \frac{2\delta v}{ ( 1-q ) ^{2}}+\frac{d\gamma }{dq} \\ \overbrace{=}^{\text{By (18) and (19)}} &3\sigma ^{2}\frac{2- ( q+1 ) ( 1+\frac{\mu ^{2}}{\sigma ^{2}} ) }{2 ( 1-q ) ^{3}\delta } \biggl( 1-\frac{2v}{ ( 1-q ) } \biggr) +\frac{\mu -2\delta v}{ ( 1-q ) ^{2}}. \end{aligned}$$

Since $\mu >\sqrt{3}\sigma$, $2- ( q+1 ) ( 1+\frac{\mu ^{2}}{\sigma ^{2}} ) <0$. To show $\frac{dy^{\ast } ( q ) }{dq}>0$, sufficient conditions are

$$\begin{aligned} (\mathrm{C1}) :&\quad 1-\frac{2v}{ ( 1-q ) }<0; \\ (\mathrm{C2}) :&\quad \mu -2\delta v>0. \end{aligned}$$

Condition (C1) holds since $v>\frac{1}{2}$ implies $\frac{2v}{ ( 1-q ) }>1$ for all q∈[0,1]. By the definition of δ(q), condition (C2) is equivalent to

$$ \frac{\mu ^{2}}{12v^{2}\sigma ^{2}} ( 1-q ) ^{2}>1-q \biggl( 1+\frac{\mu ^{2}}{\sigma ^{2}} \biggr). $$

The left-hand side of above inequality is a convex function of q and is equal to $\frac{\mu ^{2}}{12v^{2}\sigma ^{2}}$ when q=0. The right-hand side of above inequality is a linear function of q with negative slope and is equal to 1 at q=0. Together with $\mu >2\sqrt{3}\sigma v$ that implies $\frac{\mu ^{2}}{12v^{2}\sigma ^{2}}>1$, there exists $\hat{q}\in [ 0,1 ]$ such that for $q\in ( 0,\hat{q} )$ condition (C2) holds. This completes the proof of $\frac{dx_{r}^{\ast } ( q ) }{dq}>0$.

Now we show $\frac{dx_{k}^{\ast } ( q ) }{dq}<0$ under the given condition. This is a direct implication of $\frac{dy^{\ast } ( q ) }{dq}>0$ and $\frac{dx_{r}^{\ast } ( q ) }{dq}>0$ as $x_{k}^{\ast }=d-y^{\ast }x_{r}^{\ast }$. □

1.2 A.2 Optimal procurement decisions when demand is deterministic

First, we solve for the optimal level of reserved capacity $x_{k}^{*}(x_{r})$ given the quantity x _r ordered from the regular supplier. Notice that if x _r =0, by (8), we have the profit function $\pi(0,x_{k})=\lim_{x_{r}\rightarrow 0}\pi(x_{r},x_{k})=(p-c_{e})x_{k}-l(d-x_{k})-c_{k}x_{k}=(p+l-c_{e}-c_{k})x_{k}-ld$, where x _k ∈[0,d]. Hence, $x_{k}^{*}(0)=d$ if p+l>c _e +c _k ; otherwise, $x_{k}^{*}(0)=0$. If x _r >0, then we have $\frac{\partial \pi(x_{r},x_{k})}{\partial x_{k}}=(l+p-c_{e})q-c_{k}+(l+p-c_{e})(1-q)G(\frac{d-x_{k}}{x_{r}})$, where $F(\cdot\mid x_{r})=q+(1-q)G(\frac{\cdot}{x_{r}})$. Since l+p>c _e , π(x _r ,x _k ) is concave in x _k . Hence, we have the optimal reservation capacity

$$ x_k^*(x_r)= \left \{ \begin{array}{l} d,\quad \hbox{if $c_{k}\leq(l+p-c_{e})q$;} \\ d-x_rG^{-1}(1-\frac{l+p-c_e-c_k}{(l+p-c_e)(1-q)}),\\ \quad\hbox{if $(l+p-c_{e})q<c_{k}<(l+p-c_{e})(q+(1-q)G(\frac{d}{x_{r}}))$;} \\ 0,\quad \hbox{if $c_{k}\geq(l+p-c_{e})(q+(1-q)G(\frac{d}{x_{r}}))$.} \end{array} \right . $$

(20)

We let the firm’s optimal profit be $\pi^{*}(x_{r})=\pi(x_{r},x_{k}^{*}(x_{r}))$. Finally, we solve for the optimal order quantity from the regular supplier $x_{r}^{*}$. By (8) and (20) and the envelope theorem (see, e.g., p. 964 Mas-Colell et al. 1995), we have

$$\begin{aligned} \frac{d\pi^*(x_r)}{dx_r} =& c(q,G)+s(1-q)\int_0^{\frac{d}{x_r}}G( \xi)d\xi -c_e(1-q)\int_{\frac{d-x_k^*(x_r)}{x_r}}^{\frac{d}{x_r}}G(\xi)d \xi \\ &{}-(l+p) (1-q)\int_0^{\frac{d-x_k^*(x_r)}{x_r}}G(\xi)d\xi \\ &{}-(s-c_e) (1-q)\frac{d}{x_r}G\biggl(\frac{d}{x_r} \biggr) \\ &{}+(l+p-c_e) (1-q)\frac{d-x_k^*(x_r)}{x_r}G\biggl(\frac{d-x_k^*(x_r)}{x_r} \biggr) \\ =& c(q,G)+(c_e-s) (1-q)\int_0^{\frac{d}{x_r}} \xi g(\xi)d\xi \\ &{}+(l+p-c_e) (1-q)\int_0^{\frac{d-x_k^*(x_r)}{x_r}}\xi g(\xi)d\xi \end{aligned}$$

(21)

where c(q,G)=s(1−q)E[ξ _r ]−(λ+(1−λ)(1−q)E[ξ _r ])c _r and the last equation follows from $\int_{0}^{y}G(\xi)d\xi-yG(y)=-\int_{0}^{y}\xi g(\xi)d\xi$. By (20) and (21), we have

$$ \frac{d\pi^*(x_r)}{dx_r}= \left \{ \begin{array}{l} c(q,G)+(c_e-s)(1-q)\int_0^{\frac{d}{x_r}}\xi g(\xi)d\xi,\quad \hbox{if $\frac{c_{k}}{l+p-c_{e}}\leq q$;} \\ c(q,G)+(l+p-c_e)(1-q)\int_0^{y^*}\xi g(\xi)d\xi+(c_e-s)(1-q)\int_0^{\frac{d}{x_r}}\xi g(\xi)d\xi,\\ \quad\hbox{if $q<\frac{c_{k}}{l+p-c_{e}}<q+(1-q)G(\frac{d}{x_{r}})$;} \\ c(q,G)+(l+p-s)(1-q)\int_0^{\frac{d}{x_r}}\xi g(\xi)d\xi,\quad \hbox{if $\frac{c_{k}}{l+p-c_{e}}\geq q+(1-q)G(\frac{d}{x_{r}})$,} \end{array} \right . $$

(22)

where $y^{*}=G^{-1}(1-\frac{l+p-c_{e}-c_{k}}{(l+p-c_{e})(1-q)})$.

Since we assume c(q,G)<0, by (22) we have three cases that depend on the cost of reserving capacity from the backup supplier.

Case 1 ($\frac{c_{k}}{l+p-c_{e}}\leq q$)::

The optimal order quantity from the regular supplier is $x_{r}^{*}= \inf\{x_{r}\geq 0\mid c(q,G)+(c_{e}-s)(1-q)\int_{0}^{\frac{d}{x_{r}}}\xi g(\xi)d\xi\leq 0\}$. If c _e (1−q)E[ξ _r ]<(λ+(1−λ)(1−q)E[ξ _r ])c _r , then $x_{r}^{*}=0$. Otherwise, $x_{r}^{*}$ is the unique solution of $c(q,G)+(c_{e}-s)(1-q)\int_{0}^{\frac{d}{x_{r}}}\xi g(\xi)d\xi=0$. By (20), the optimal level of reserved capacity from the backup supplier is $x_{k}^{*}=x_{k}^{*}(x_{r}^{*})=d$. The firm reserves d units of capacity to satisfy all customer demand from the backup supplier, since the reservation cost (c _k ) is low.

Case 2 ($\frac{c_{k}}{l+p-c_{e}}\geq 1$)::

The optimal order quantity from the regular supplier is $x_{r}^{*}= \inf\{x_{r}\geq 0\mid c(q,G)+(l+p-s)(1-q)\int_{0}^{\frac{d}{x_{r}}}\xi g(\xi)d\xi\leq 0\}$. If (l+p)(1−q)E[ξ _r ]<(λ+(1−λ)(1−q)E[ξ _r ])c _r , then $x_{r}^{*}=0$. Otherwise, $x_{r}^{*}$ is the unique solution of $c(q,G)+(l+p-s)(1-q)\int_{0}^{\frac{d}{x_{r}}}\xi g(\xi)d\xi=0$. By (20), the optimal level of reserved capacity from the backup supplier is $x_{k}^{*}=x_{k}^{*}(x_{r}^{*})=0$. The firm reserves zero capacity from the backup supplier, since the reservation cost (c _k ) is high.

Case 3 ($q<\frac{c_{k}}{l+p-c_{e}}<1$)::

By (22), we have $\frac{d\pi^{*}(x_{r})}{dx_{r}}=J(x_{r})$, where

$$ J(x_r)= \left \{ \begin{array}{l} c(q,G)+(l+p-c_e)(1-q)\int_0^{y^*}\xi g(\xi)d\xi\\ \quad{}+(c_e-s)(1-q)\int_0^{\frac{d}{x_r}}\xi g(\xi)d\xi,\quad \hbox{if $x_{r}<\frac{d}{y^{*}}$;} \\ c(q,G)+(l+p-s)(1-q)\int_0^{\frac{d}{x_r}}\xi g(\xi)d\xi,\quad \hbox{if $x_{r}\geq \frac{d}{y^{*}}$.} \end{array} \right . $$

(23)

Since J(x _r ) is decreasing in x _r , π ^∗(x _r ) is concave in x _r . The optimal order quantity from the regular supplier is $x_{r}^{*}=\inf\{x_{r}\geq 0\mid J(x_{r})\leq 0\}$. If $c_{e}(1-q)E[\xi_{r}]+ (l+p-c_{e})(1-q)\int_{0}^{y^{*}}\xi g(\xi)d\xi<(\lambda+(1-\lambda)(1-q)E[\xi_{r}])c_{r}$, then $x_{r}^{*}=0$.

If the regular supplier’s random yield ξ _r follows a uniform distribution on [γ−δ,γ+δ], then we have a closed form solution of $x_{r}^{*}$. Notice that E[ξ _r ]=γ and $\operatorname{Var}[\xi_{r}]=\frac{\delta^{2}}{3}$.

Case 1 ($\frac{c_{k}}{l+p-c_{e}}\leq q$)::

In this case, we have $x_{k}^{*}=d$. If c _e (1−q)γ<(λ+(1−λ)(1−q)γ)c _r , then $x_{r}^{*}=0$. Otherwise, $x_{r}^{*}=d/\sqrt{\frac{-4c(q,G)\delta}{(c_{e}-s)(1-q)}+(\gamma-\delta)^{2}}$.

Case 2 ($\frac{c_{k}}{l+p-c_{e}}\geq 1$)::

In this case, we have $x_{k}^{*}=0$. If $(l+p)(1-q)\gamma<(\lambda+(1-\lambda) (1-q)\gamma)c_{r}$, then $x_{r}^{*}=0$. Otherwise, $x_{r}^{*}=d/\sqrt{\frac{-4c(q,G)\delta}{(l+p-s)(1-q)}+(\gamma-\delta)^{2}}$.

Case 3 ($q<\frac{c_{k}}{l+p-c_{e}}<1$)::

Notice that $y^{*}=\gamma-\delta+2\delta\frac{c_{k}-q(l+p-c_{e})}{(l+p-c_{e})(1-q)}$ and $\int_{\gamma-\delta}^{y^{*}}\xi g(\xi)d\xi=\frac{c_{k}-q(l+p-c_{e})}{(l+p-c_{e})(1-q)} [\gamma-\frac{\delta(l+p-c_{e}-c_{k})}{(l+p-c_{e})(1-q)} ]$.

• If $c_{e}(1-q)\gamma+[c_{k}-q(l+p-c_{e})] [\gamma-\frac{\delta(l+p-c_{e}-c_{k})}{(l+p-c_{e})(1-q)} ]<(\lambda+(1-\lambda)(1-q)\gamma)c_{r}$, then $x_{r}^{*}=0$ and $x_{k}^{*}=d$.

• If $s(1-q)\gamma+[c_{k}-q(l+p-c_{e})] [\gamma-\frac{\delta(l+p-c_{e}-c_{k})}{(l+p-c_{e})(1-q)} ]\frac{l+p-s}{l+p-c_{e}} >(\lambda+(1-\lambda) (1-q)\gamma)c_{r}$, then $x_{r}^{*}=d/\sqrt{\frac{-4c(q,G)\delta}{(l+p-s)(1-q)}+(\gamma-\delta)^{2}}$ and $x_{k}^{*}=0$.

• Otherwise, $x_{r}^{*}=d/\{\{-4c(q,G)\delta -4\delta[c_{k}-q(l+p-c_{e})] [\gamma-\frac{\delta(l+p-c_{e}-c_{k})}{(l+p-c_{e})(1-q)} ]\}/ \{(c_{e}-s)(1-q)\}+(\gamma-\delta)^{2}\}^{1/2}$ and $x_{k}^{*}=d-x_{r}^{*}y^{*}$.