Supply planning models for a remanufacturer under just-in-time manufacturing environment with reverse logistics

Abstract

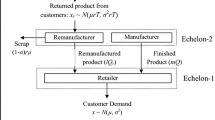
We study a supply planning problem in a manufacturing system with two stages. The first stage is a remanufacturer that supplies two closely-related components to the second (manufacturing) stage, which uses each component as the basis for its respective product. The used products are recovered from the market by a third-party logistic provider through an established reverse logistics network. The remanufacturer may satisfy the manufacturer’s demand either by purchasing new components or by remanufacturing components recovered from the returned used products. The remanufacturer’s costs arise from product recovery, remanufacturing components, purchasing original components, holding inventories of recovered products and remanufactured components, production setups (at the first stage and at each component changeover), disposal of recovered products that are not remanufactured, and coordinating the supply modes. The objective is to develop optimal production plans for different production strategies. These strategies are differentiated by whether inventories of recovered products or remanufactured components are carried, and by whether the order in which retailers are served during the planning horizon may be resequenced. We devise production policies that minimize the total cost at the remanufacturer by specifying the quantity of components to be remanufactured, the quantity of new components to be purchased from suppliers, and the quantity of recovered used products that must be disposed. The effects of production capacity are also explored. A comprehensive computational study provides insights into this closed-loop supply chain for those strategies that are shown to be NP-hard.

Appendix for “Supply Planning Models for a Remanufacturer under Just-in-Time Manufacturing Environment with Reverse Logistics”

1.1 Appendix 1: proof of Theorem 3

Theorem 3

Problem PR3 is NP-hard in the ordinary sense when $L_r > \mu \beta \frac{Q_0}{n},$ where Q ₀ = min[Q ₁, Q ₂].

Proof

The reduction is from Even–Odd Partition. Consider an arbitrary instance of Even–Odd Partition.

Even–Odd Partition (Garey et al. 1988): given an integer B, a set of 2t positive integers A = {a ₁, a ₂,…,a _2t−1, a _2t } such that a ₁ < a ₂ <⋯< a _2t−1 < a _2t , and $\sum\nolimits_{a_i\in A} a_i= 2B,$ does there exist a partition of A into two disjoint subsets A ₁ and A ₂ such that $\sum\nolimits_{a_k\in A_1}a_k=\sum\nolimits_{a_j\in A_2}a_j=B,\,|A_1| = |A_2|=t,$ and that each of A ₁, A ₂ contains exactly one of a _2i−1 and a _2i for i = 1, 2,…,t?

Given an instance of Even–Odd Partition, we construct a specific instance of the decision version of Problem PR3 as follows: there are 4t + 2 retailers. The system parameters are $n = 4t+2,\, \mu = \beta=1,\,L_m = 2M,\,L_r =2M,\,K = 0,\,I^P_{01} = 0,\,I^P_{02} = 0,\, c_{1} = 2,\,c_{2} = M+1,\,u_{1} = 1,\,u_{2} = 1,\,g_{1} = 0,\, g_{2} = 0,\,h^P_{1} = 0,\,h^P_{2} = 0$ and α = 2M(tM + B). The values of d _ij , i = 1, 2,…,n, j = 1, 2 are given as follows:

$$ \begin{array}{ll} &d_{11}=M+B,\quad d_{12}=M-B;\\ &d_{3k-1,1}=M-a_{2k-1}, \quad d_{3k,1}=M-a_{2k}, \quad d_{3k+1,1}=0,\quad k=1,\, 2,\ldots, t;\\ &d_{3k-1,2}=M+a_{2k-1}, \quad d_{3k,2}=M+a_{2k},\quad d_{3k+1,2}=2M, \quad k=1,\, 2, \ldots, t;\\ &d_{3t+2,1}=M+B, \quad d_{3t+2,2}=M-B;\\ &d_{k+3t+2,1}=2M, \quad d_{k+3t+2,2}=0, \quad k=1,\, 2, \ldots, t.\\ \end{array} $$

Note that Q ₀ = Q ₁ = Q ₂ = (4t + 2)M and $\sum\nolimits_{a_i \in A} a_i = 2B.$ A threshold value, D = 3(3t + 2)M + M(tM + B) + B, where we set M = 4B.

The decision problem can be stated as follows: “Does there exist a production schedule, ν = {x _ij , y _ij , s _ij |i = 1, 2,…,4t + 2; j = 1, 2} such that the cost of the schedule Π _ν ≤ D = 3(3t + 2)M + M(tM + B) + B?”

If part: suppose there exists a solution to the Even–Odd Partition problem. Without loss of generality, we let the solution be a ₁ + a ₄+⋯+a _2t  = a ₂ + a ₃+⋯+a _2t−1 + B, where A ₁ = {a ₁, a ₄,…,a _2t } and A ₂ = {a ₂, a ₃,…,a _2t−1}, where subsets A ₁, A ₂ are disjoint and |A ₁| = |A ₂| = t. Note that the sequence of retailers is fixed: (R ₁, R ₂,…,R _4t+2). We propose the production schedule ν as shown in Table 12. Table 13 calculates the cost for schedule ν: Π _ν  = D = 3(3t + 2)M + M(tM + B) + B. (In these tables, for convenience, we let α _ij be the administrative cost for product P _j in period i.) This completes the proof for the If part.

Table 12 Production schedule ν

Table 13 The total cost calculation Π _ν

We list below the properties of the production schedule ν (Table 12) and the decision problem instance of Problem PR3 for facilitating the proof of the only if part.

• The demand of product P _j ,  j = 1, 2 during each period is met by using only one mode (either by remanufacturing component C _j or by purchasing component C _j ). That is, there is no administrative cost: α _ij  = 0 for i = 1, 2,…,4t + 2; j = 1, 2.

• As Q ₀ = Q ₁ = Q ₂ = (4t + 2)M and $\frac{Q_0}{n}=M,\,M$ units of product P ₁ (resp., P ₂) are recovered during each period i, i = 1, 2,…,4t + 2.

• One period’s demand for product P ₂ in the set {d _3k−1,2 = M + a _2k−1, d _3k,2 = M + a _2k }, for each k, k = 1, 2,…,t, is satisfied only by remanufacturing component C ₂ and the other is satisfied only by purchasing component C ₂.

• The demand for product P ₂,  d _3k+1,2 = 2M, for each k, k = 1, 2,…,t, is satisfied only by remanufacturing component C ₂.

• One period’s demand for product P ₁ in {d _3k−1,1 = M − a _2k−1, d _3k,1 = M − a _2k }, for each k, k = 1, 2,…,t, is satisfied only by remanufacturing component C ₁, and the other is satisfied only by purchasing component C ₁.

• There is no disposal cost for either recovered product P ₁ or P ₂, as g ₁ = g ₂ = 0.

• $I^P_{3t+2,1} = Mt,$ i.e., the inventory level of recovered product P ₁ is accumulated up to Mt units in order to remanufacture 2M units of component C ₁ during each period i, i = 3t + 3, 3t + 4,…,4t + 2.

• There is no inventory carrying cost for either recovered product P ₁ or P ₂, as $h^P_1=h^P_2=0.$

Only If part: suppose there exists a production schedule, ν _o  = {x _ij , y _ij , s _ij |i = 1, 2,…,4t + 2; j = 1, 2} such that $\Pi_{\nu_o} \leq D= 3(3t+2)M + M(tM+B) +B.$ We now prove that there exists an Even–Odd Partition by establishing a number of claims. We first develop a lower bound L on the total cost $\Pi_{\nu_o}$ of the production schedule ν _o .

Claim A1

$\Pi_{\nu_o} \geq L= 4(2t+1)M.$

Proof

The lower bound L consists of two cost components, L = L ₁ + L ₂, and is estimated as shown in Table 14.

• The total demand of product P ₁ during the planning horizon is $\sum\nolimits_{i=1}^{4t+2} d_{i1} = M(4t+2).$ The lower bound on the cost of satisfying the demand of product P ₁ is L ₁ = M(4t + 2)u ₁ = M(4t + 2) since u ₁ < c ₁.

• The total demand of product P ₂ during the planning horizon is $\sum\nolimits_{i=1}^{4t+2} d_{i1} = M(4t+2).$ The lower bound on the cost of satisfying the demand of product P ₂ is L ₂ = M(4t + 2)u ₂ = M(4t + 2) since u ₂ < c ₂.

Table 14 Lower bound on the total cost, $\Pi_{\nu_o}$

By adding these two costs, we obtain $\Pi_{\nu_o} \geq L= L_1+L_2=4(2t+1)M.$ $\square$

Claim A2

In ν _o , the demand of product P _j ,  j = 1, 2, during each period is met by using only one mode (either by remanufacturing component C _j or by purchasing component C _j ).

Proof

The result follows from $\Pi_{\nu_o} \geq L +\alpha > D.$ $\square$

Next, we further tighten the lower bound on the total cost, $\Pi_{\nu_o},$ by a series of claims. The idea behind the lower bound cost estimation is as follows: since u ₁ < c ₁ and u ₂ < c ₂, the remanufactured components are used to satisfy the demand of products P _j ,  j = 1, 2, whenever possible. Otherwise, components are purchased.

Claim A3

The demand for M + B units of product P ₁ cannot be satisfied by remanufacturing component C ₁ in period 1.

Proof

M units of product P ₁ are recovered in the beginning of period 1. The result follows since $I^P_{01}=0$ and the demand for product P _j ,  j = 1, 2, during each period must be met by using only one mode (Claim A2). $\square$

As a consequence of Claims A2 and A3, in period 1, M + B units of component C ₁ must be purchased and M − B units of component C ₂ may be remanufactured.

Claim A4

At least one period’s demand for product P ₂ among {d _3k−1,2 = M + a _2k−1, d _3k,2 = M + a _2k , d _3k+1,2 = 2M}, for each k, k = 1, 2,…,t, cannot be satisfied by remanufacturing component C ₂.

Proof

The total demand for product P ₂ in periods {3k − 1, 3k, 3k + 1} is 4M + a _2k−1 + a _2k , for each k, k = 1, 2,…,t. Note that 3M units of product P ₂ are recovered during periods, {3k − 1, 3k, 3k + 1}. A maximum of M recovered units of product P ₂ can be carried from previous periods because L _r  = 2M. Since remanufacturing 4M recovered units of product P ₂ cannot satisfy the total demand 4M + a _2k−1 + a _2k for product P ₂, the result follows. Thus, at least one demand in periods {3k − 1, 3k, 3k + 1} cannot be satisfied by remanufacturing component C ₂.

Suppose E ₁ and E ₂ are two disjoint subsets such that $A=E_1 \cup E_2,$ and that each of E ₁, E ₂ contains exactly one of a _2k−1 and a _2k , for k = 1, 2,…,t. Assume that set E ₁ corresponds to periods where component C ₂ is purchased (Claim A4) and $\sum\nolimits_{a_{i}\in E_1} a_{i} =B+\theta,$ where −B < θ < B. Note that $\sum\nolimits_{a_{i}\in E_2} a_{i} =B-\theta.$

Claim A5

In a minimum cost solution, the total cost of purchasing component C ₂ (resp., C ₁) in periods {3k − 1, 3k, 3k + 1}, k = 1, 2,…,t, is at least $(tM+\sum\nolimits_{a_{i}\in E_1} a_{i})c_2$ (resp., $(tM- \sum\nolimits_{a_{i}\in E_2} a_{i})c_1$).

Proof

As a consequence of Claim A4, one demand in periods {3k − 1, 3k, 3k + 1} must be satisfied by purchasing component C ₂. The minimum demand in those period is M + a _2k−1 (or M + a _2k ). Thus, the number of units of component C ₂ purchased is at least $tM+\sum\nolimits_{a_{i}\in E_1} a_{i},$ in all periods {3k − 1, 3k, 3k + 1}. In order to generate the minimum cost solution, we may assume that remanufacturing component C ₂ is done in all other periods. This implies that the demand M − a _2k (or M − a _2k−1) of product P ₁ in periods 3k (or 3k − 1), k = 1, 2,…,t, must be satisfied by purchasing component C ₁. The total demand that must be satisfied by purchasing component C ₁ for k = 1, 2,…,t, is at least $tM-\sum\nolimits_{a_{i}\in E_2}a_{i}.$ $\square$

We now establish a tighter lower bound L′ that consists of five cost components: L′ = L ₁ + L ₂ + L ₃ + L ₄ + L ₅.

Claim A6

$\Pi_{\nu_o} \geq L^{\prime}= L_1+L_2+L_3 +L_4 +L_5 = 9Mt+6M+M^2t+(M+1)B+(M+1)\theta.$

Proof

The lower bound L′ consists of five cost components. L ₁ + L ₂ is estimated as before (Table 14). L ₁ is estimated by assuming that all demand is satisfied by remanufacturing components C ₁. From Claim A5, at least Mt − B + θ units of components C ₁ must be purchased in all periods {3k − 1, 3k, 3k + 1}, k = 1, 2,…,t. L ₃ quantifies the additional cost of purchasing and L ₃ = (Mt − B + θ)(c ₁ − u ₁) = Mt − B + θ. L ₂ is estimated by assuming that all demand is satisfied by remanufacturing component C ₂. From Claim A5, at least Mt + B + θ units of component C ₂ must be purchased in all periods {3k − 1, 3k, 3k + 1}, k = 1, 2,…,t. L ₄ quantifies the additional cost of purchasing, where L ₄ = (Mt + B + θ)(c ₂ − u ₂) = M ² t + MB + Mθ. Due to Claims A2 and A3, the demand M + B of product P ₁ in period 1 must be satisfied by purchasing component C ₁. It is economical to satisfy the demand M + B of product P ₁ in period 3t + 2 (resp., the demand M − B of product P ₂ in period 3t + 2) by purchasing (resp., remanufacturing) components C ₁ (resp., C ₂). L ₅ quantifies the additional cost of purchasing components C ₁ in periods 1 and 3t + 2 which is L ₅ = (2M + 2B)(c ₁ − u ₁) = 2M + 2B. $\square$

Claim A7

θ ≤ 0.

Proof

Suppose θ > 0. Then $\Pi_{\nu_o} \geq L^{\prime}=9Mt+6M+M^2t+(M+1)B+(M+1)\theta \geq 9Mt+6M+M^2t+(M+1)B+(M+1)>D.$ $\square$

Claim A7 implies that $\sum\nolimits_{a_{i}\in E_1} a_{i} \leq B.$ That is, $\sum\nolimits_{a_{i}\in E_2} a_{i} \geq B.$

Claim A8

The demand M  − B for product P ₂ in period 1 must be satisfied by remanufacturing component C ₂.

Proof

As a consequence of Claim A7, the total units of component C ₂ purchased cannot be larger than tM + B. If the demand M − B for product P ₂ in period 1 is satisfied by purchasing, then the total number of units of component C ₂ purchased is $tM+\sum\nolimits_{a_{i}\in E_1} a_{i}+M-B>tM+B.$ $\square$

Claim A9

$\sum\nolimits_{a_{i}\in E_2} a_{i} = B.$

Proof

Similar to the argument in Claim A8, the demand in the following periods must be satisfied by remanufacturing components C ₂: periods corresponding to E ₂, periods 3k + 1, k = 1, 2,…,t, and 3t + 2. Note that the total amount of product P ₂ recovered in periods 1, 2,…,3t + 1 is U ₁ = (3t +1)M. The total demand that must be satisfied by remanufacturing component C ₂, in period 1, periods corresponding to E ₂ and periods 3k + 1, k = 1, 2,…,t is $U_2=M-B + Mt +\sum\nolimits_{a_{i}\in E_2} a_{i} +2Mt.$ Note that U ₁ = U ₂, which implies that $\sum\nolimits_{a_{i}\in E_2} a_{i}=B.$

Claims A7 and A9 imply that $\sum\nolimits_{a_i \in E_1} a_i = \sum\nolimits_{a_i \in E_2} a_i= B$ and |E ₁| = |E ₂| = t, where $E_1 \subset A,\,E_2=A-E_1,$ and a solution to the Even–Odd Partition problem exists. This completes the proof of Theorem 3. $\square$

1.2 Appendix 2: proof of Theorem 4

Theorem 4

Problem PR4 is NP-hard in the strong sense when $L_r > \mu \beta \frac{Q_0}{n},$ where $Q_0=\hbox{min}[Q_1,\, Q_2].$

Proof

The reduction is from NMTS (Garey and Johnson 1979).

NMTS: given three sets of positive integers $\bar{E}=\{e_1,\,e_2,\ldots ,e_t\},\, \bar{F}=\{f_1,\, f_2,\ldots, f_t\},\,\bar{W}=\{w_1,\, w_2,\ldots, w_t\},$ can $\bar{E}\cup \bar{F}$ be partitioned into t disjoint subsets Γ ₁,…,Γ _t with $\Gamma_i=\{e_{k_i},\, f_{r_i}\}$ such that $w_i=e_{k_i} + f_{r_i},$ for i = 1, 2,…,t?

Consider the following instance of the problem: the retailer set consists of three types of retailers, where each type consists of t retailers: ${{\mathcal{R}}=\{R_{e_i},\,R_{f_i},\,R_{w_i}| 1 \leq i \leq t\}}$ and n = 3t. The demand of products P ₁ and P ₂ for retailer $R_{e_i}$ are M + 2T + e _i and M − 2T − e _i , respectively, for retailer $R_{f_i}$ are M + T + f _i and M − T − f _i , respectively, and for retailer $R_{w_i}$ are M − 3T − w _i and M + 3T + w _i , respectively, for i = 1, 2,…,t (see Fig. 11). It is also assumed that W = E + F, where $E = \sum\nolimits_{i=1}^{t} e_i,\,F = \sum\nolimits_{i=1}^{t} f_i,$ and $W=\sum\nolimits_{i=1}^{t}w_i.$ The system parameters are $\mu =\beta=1,\,\alpha=0,\, L_m=2M,\, L_r=M+2T+W,\, c_{1}=M+2,\, c_{2}=1,\,u_{1}=1,\, u_{2}=1,\, g_{1}=4,\, g_{2}=1,\, h^P_{1}=1,$ and $h^P_{2}=3.$ The decision problem can be stated as follows: “Does there exist a production schedule, $\nu=\{x_{ij},\,y_{ij},\,s_{ij}|i=1,\,2,\ldots,3t;\,j=1,\,2\},$ and a sequence of retailers σ with total cost $\Pi_{(\nu, \sigma)} \leq D= K+9Mt+4Tt+W+F?$”

Fig. 11

Inventory and purchasing decisions in ν for σ

We set T = 6W and M = 24Wt + W + F, and therefore D = K + 9Mt + M. We let K = 9Mt + M + 1.

If part: suppose there exists a solution to the NMTS problem. Let the solution be e _i + f _i  = w _i , i = 1, 2,…,t. Consider a sequence of retailers σ, where $\sigma=(R_{w_1},\,R_{e_1},\,R_{f_1},\,R_{w_2},\,R_{e_2},\,R_{f_2},\ldots,R_{w_t},\,R_{e_t},\,R_{f_t}).$ Note that there is no initial inventory of recovered products P ₁ and P ₂, i.e., $I_{01}^P = I_{02}^P = 0.$ We propose the production schedule ν for a sequence of retailers σ as shown in Fig. 11 and Table 15. Table 16 calculates the cost for $(\nu,\,\sigma):\,\Pi_{(\nu,\sigma)}=D=K+9Mt+4Tt+W+F$ as the proof for the If part. $\square$

Table 15 Production schedule $\nu=\{x_{ij},\, y_{ij},\, s_{ij}|i=1,\,2,\ldots, 3t;\,j=1,\,2 \}$ and a sequence of retailers σ

Table 16 The total cost calculation Π _(ν,σ)

In order to facilitate the proof of the only if part we list below the properties of the production schedule ν for a sequence of retailers σ:

• There is one setup at the beginning of period 1 (cost K). Note that all recovered units of the product P ₁ are remanufactured in order to obtain component C ₁ during the planning horizon.

• The required units of component C ₂ are purchased, and all recovered units of product P ₂ are disposed during each period.

• There is no inventory carrying cost for the recovered product P ₂ since the demand of product P ₂ is satisfied by purchasing the original component C ₂ in each period $(I^P_{i2}=0;\,\,i=1,\,2,\ldots,3t).$

• Since L _r  = M + 2T + W, there is a certain advantage in carrying inventories of the recovered product P ₁, i.e., $I^P_{i1} \geq 0,\,i=1,\,2,\ldots,3t.$

Only If part: suppose there exists a production schedule ν _o , where $\nu_o=\{x_{ij},\, y_{ij},\, s_{ij}|i=1,\,2,\ldots, 3t;\, j=1,\,2\},$ and a sequence of retailer σ _o such that $\Pi_{(\nu_o,\sigma_o)} \leq D= K+9Mt+4Tt+W+F.$ We first characterize the production schedule ν _o and then argue that for ν _o , the sequence of retailers σ _o can only take the following form: $\sigma_o=(R_{w_1},\,R_{e_1},\,R_{f_1},\,R_{w_2},\,R_{e_2},\, R_{f_2},\ldots,R_{w_t},\,R_{e_t},\,R_{f_t}).$

The following claims characterize the production schedule ν _o .

Claim B1

The production schedule ν _o has only one setup.

Proof

Suppose the production schedule ν _o has more than one setup. Then, $\Pi_{(\nu_o,\sigma_o)} \geq 2K > D,$ which contradicts the fact that $\Pi_{(\nu_o,\sigma_o)} \leq D.$ $\square$

Claim B2

In ν _o , the recovered product P ₁ is remanufactured during all periods.

Proof

As a consequence of Claim B1, either P ₁ or P ₂ must be remanufactured during all periods. If the recovered product P ₂ is remanufactured during all periods, then M recovered units of product P ₁ must be disposed during each period (cost $\sum\nolimits_{i=1}^{3t} g_{1} M=12Mt$ as g ₁ = 4). Thus, $\Pi_{(\nu_o, \sigma_o)} \geq K + 12Mt > D,$ which contradicts the fact that $\Pi_{(\nu_o,\sigma_o)} \leq D.$ The recovered product P ₁ is therefore remanufactured during all periods. $\square$

Let θ be the total number of the original component C ₁ purchased for product P ₁ in $\nu_o:\,\theta=\sum\nolimits_{i=1}^n y_{i1}.$

Claim B3

In ν _o , 3Ms recovered units of product P ₁ must be remanufactured during 3t periods and θ = 0.

Proof

As a consequence of Claim B2, 3Mt new units of component C ₂ must be purchased (cost 3Mt, as c ₂ = 1) and 3Mt recovered units of product P ₂ must be disposed (cost 3Mt, as g ₂ = 1). Note that the maximum number recovered units of product P ₁ that can be remanufactured is 3Mt, which is equal to the total demand of product P ₁ during 3t periods. Since θ is the total number of the original component C ₁ purchased for product P ₁, (3Mt − θ) recovered units of product P ₁ are remanufactured in ν _o . Thus, $\Pi_{(\nu_o,\sigma_o)}\geq K + 3Mt + 3Mt + \theta c_1 + (3Mt-\theta)u_1 = K+9Mt+ \theta(M+1)$ as c ₁ = M + 2, u ₁ = 1. If θ ≥ 1, then $\Pi_{(\nu_o,\sigma_o)}> D,$ which contradicts the fact that $\Pi_{(\nu_o,\sigma_o)} \leq D.$ Therefore, θ = 0 and 3Mt recovered units of product P ₁ must be remanufactured during the planning horizon. $\square$

Claim B4

In ν _o , any recovered product P ₁ must not be disposed during 3t periods.

Proof

The result follows from Claim B3. $\square$

As a consequence of Claim B3, new component C ₁ cannot be purchased because θ = 0. Thus, the total demand of product P ₁ (resp., P ₂) must be satisfied by the remanufactured component C ₁ (resp., the new component C ₂) during 3t periods. Therefore, in $\nu_o,\,\Pi_{(\nu_o,\sigma_o)} \geq K+9Mt.$ We now consider the total inventory carrying cost of the recovered product P ₁ in (ν _o ,  σ _o ), denoted by $L_{(\nu_o,\sigma_o)} = L_{(\nu_1,\rho_1)}+ L_{(\nu_2,\rho_2)}+ \cdots + L_{(\nu_t,\rho_t)},$ where:

• $\sigma_o=(\rho_1,\, \rho_2, \ldots, \rho_t),$ and a subsequence of three retailers $\rho_i= (R_{w_i},\,R_{e_i},\,R_{f_i})\,i=1,\,2,\ldots, t,$

• $\nu_o=(\nu_1,\, \nu_2, \ldots, \nu_t),$ and ν _i is the production schedule for periods 3i − 2, 3i − 1, and 3i, i = 1, 2,…,t,

• $L_{(\nu_i,\rho_i)}$ is the inventory carrying cost of the subsequence ρ _i , i = 1, 2,…,t.

We therefore note that $\Pi_{(\nu_o,\sigma_o)} = K + 9Mt + L_{(\nu_o,\sigma_o)}.$

Claim B5

$L_{(\nu_o,\sigma_o)} \leq M.$

Proof

Since $\Pi_{(\nu_o,\sigma_o)} \leq D,$ we must have $L_{(\nu_o,\sigma_o)} \leq M.$ $\square$

We now find all possible subsequences for ν ₁ (i.e., subsets of the first 3 retailers) and the corresponding cost $L_{(\nu_1,\rho_1)}.$

Claim B6

The first retailer served in the subsequence ρ ₁ must be of type $R_{w_i}.$

Proof

If a retailer of type $R_{e_i}$ or $R_{f_i}$ is scheduled first in ρ ₁, then we must purchase the original component C ₁ in order to satisfy the demand of product P ₁ in period 1, contradicting the fact that θ = 0 (Claim B3). $\square$

Claim B7

In ν ₁, 3T + w ₁ recovered units of product P ₁ beyond the demand during period 1 must be carried over for periods 2 and 3.

Proof

The result follows from Claims B4 and B6. $\square$

There are eight possible subsequences for ρ ₁. Table 17 illustrates the inventory level for the recovered product P ₁ in the subsequence ρ ₁ and the corresponding inventory cost $L_{(\nu_1,\rho_1)}^l,\,l=1,\,2,\ldots, 8.$ Note that $L_{(\nu_1,\rho_1)}^8 = \hbox{min}[L_{(\nu_1,\rho_1)}^1,\, L_{(\nu_1,\rho_1)}^2, \ldots,L_{(\nu_1,\rho_1)}^8].$ Moreover, Subsequence 8 providing the minimum inventory cost is feasible only when $w_{i} \geq e_{r_{i}}+f_{t_{i}}.$ We let $\sigma^*_o= (\rho^*_1,\, \rho^*_2, \ldots, \rho^*_t)$ be the minimum inventory cost solution for production schedule ν _o .

Table 17 The inventory level for the recovered product P ₁ for all possible subsequences for ρ ₁

Claim B8

In the minimum inventory cost solution $\sigma^*_o=(\rho^*_1,\, \rho^*_2, \ldots, \rho^*_t),$ each Subsequence $\rho^*_i,\,i=1,\,2,\ldots, t$ must take the form of Subsequence 8.

Proof

We use mathematical induction to prove this result. The statement of Claim B8 is true for t = 1 (see Table 17). Assume that the statement of the claim is true for t = k. We now show that it holds for t = k + 1. Note that the inventory at the end of period 3k in sequence $(\rho^*_1,\, \rho^*_2, \ldots, \rho^*_k)$ is $(\sum\nolimits_{i=1}^{k} w_i-\sum\nolimits_{i=1}^{k} e_{r_i}-\sum\nolimits_{i=1}^{k}f_{t_i}).$ Moreover, in order for sequence $(\rho^*_1,\, \rho^*_2, \ldots, \rho^*_k)$ to be feasible, we must have $\sum\nolimits_{i=1}^{\ell}w_i \geq \sum\nolimits_{i=1}^{\ell} e_{r_i}+\sum\nolimits_{i=1}^{\ell} f_{t_i},$ for $\ell=1,\,2,\ldots, k$ (Claim B3). If a retailer of type $R_{e_i}$ or $R_{f_i}$ is scheduled in the first position in $\rho^*_{k+1},$ then we must purchase the original component C ₁ in order to satisfy the demand of product P ₁ in period 3k + 1, contradicting the fact that θ = 0 (Claim B3). The first retailer served in the subsequence $\rho_{k+1}^{*}$ must therefore be of type $R_{w_i}$ and $\rho^*_{k+1}$ must take the form of Subsequence 8 in order to form the minimum inventory cost solution for sequence $(\rho^*_1,\, \rho^*_2, \ldots, \rho^*_k,\, \rho^*_{k+1}).$ This completes the proof of this claim. $\square$

Claim B9

$L_{(\nu_o,\sigma_o)} \geq M,$ if $\sigma_o=\sigma^*_o,$ where $\sigma^*_o=(\rho^*_1,\, \rho^*_2, \ldots, \rho^*_t).$

Proof

Recall that each $\rho^*_i,\,i=1,\,2,\ldots, t,$ takes the form of Subsequence 8. Observe that $\sigma_o=(\rho^*_1,\, \rho^*_2, \ldots, \rho^*_t)$ is feasible since the set of retailers consists of t of each of the three types: $R_{w_i},\,R_{e_i},$ and $R_{f_i}.$ Assuming that the inventory level at the beginning of period (3i − 2), i = 1, 2,…,t, is zero (i.e., inventory level at the beginning of each subsequence $\rho^*_i$ is zero), we develop the following lower bound: $L_{(\nu_o,\sigma_o)} \geq 4Tt+ 3\sum\nolimits_{i=1}^{t} w_i- 2\sum\nolimits_{i=1}^{t} e_{r_i}- \sum\nolimits_{i=1}^{t} f_{t_i} = 4Tt+3W-2E-F = 4Tt + (W-E-F) + (W-E) + W = 4Tt + F + W = M.$ $\square$

Claim B10

$\sigma_o=\sigma^*_o,$ where $\sigma^*_o=(\rho^*_1,\, \rho^*_2, \ldots, \rho^*_t)$ and $L_{(\nu_o,\sigma_o)} = M.$

Proof

The result follows from Claims B5, B8, and B9. $\square$

Claim B11

$w_i=e_{r_i}+f_{t_i},$ for i = 1, 2,…,t, and a solution to the NMTS problem exists.

Proof

As a consequence of Claim B10, $\sigma_o=\sigma^*_o=(\rho^*_1,\, \rho^*_2, \ldots, \rho^*_t),$ where each $\rho^*_i,\,i=1,\,2,\ldots, t,$ must take the form of Subsequence 8 and $L_{(\nu_o,\sigma_o)}=M.$ If $w_{1}<e_{r_{1}}+f_{t_{1}}$ in $\rho^*_1,$ then the original components C ₁ must be purchased in order to satisfy the demand of product P ₁ in period 3. This contradicts the fact that θ = 0 (Claim B3). If $w_{1}>e_{r_{1}}+f_{t_{1}},$ we have $L_{(\nu_o,\sigma_o)} \geq M + 3\epsilon > M$ where $w_{1} = e_{r_{1}}+f_{t_{1}}+ \epsilon$ and ε > 0. This contradicts the fact that $\Pi_{(\nu_o,\sigma_o)} < D.$ Therefore, ε = 0, and $w_1=e_{r_1}+f_{t_1}.$ Continuing the above argument for each $\rho^*_i,\,i=2,\,3, \ldots, t,$ it follows that $\rho^*_i$ is feasible only when $w_{i} = e_{r_{i}}+f_{t_{i}}.$ Thus, $w_i=e_{r_i}+f_{t_i},$ for i = 1, 2,…,t, $L_{(\nu_o,\sigma_o)} = M,$ and a solution to the NMTS problem exists. $\square$

Claim B11 completes the proof of Theorem 4. $\square$

1.3 Appendix 3: proof of Theorem 5

Theorem 5

Problem PR5 is NP-hard in the ordinary sense, even if $L_r \leq \mu \beta \frac{Q_0}{n},$ where Q ₀ = min[Q ₁, Q ₂].

Proof

The reduction is from Partition (Garey and Johnson 1979).

Partition: given a set $A=\{a_1,\, a_2, \ldots, a_t\},\,a_i \in Z^+,$ for i = 1, 2,…,t, where $\sum\nolimits_{a_i \in A} a_i = 2B,$ do there exist two disjoint subsets $A_j \subset A$ for j = 1, 2, such that $\sum\nolimits_{a_k \in A_1} a_k = B$ and $\sum\nolimits_{a_j \in A_2} a_j = B?$

Consider the following instance of the problem: there are t + 2 retailers. The demands for products P ₁ and P ₂ in the first period are M + B and M − B, respectively; in the kth period they are M − a _k−1 and M + a _k−1, respectively, for k = 2, 3,…,t + 1; and in period t + 2 they are M + B and M − B, respectively (see Fig. 12). Note that $\sum\nolimits_{a_i \in A} a_i = 2B.$ The system parameters are $n=t+2,\,\mu = \beta=1,\,L_m=2M,\,L_r = M,\,K = 0,\,c_{1} = 1,\,c_{2} = M+1,\,u_{1} = 1,\,u_{2}=1,\,g_{1}=0,\,g_{2} = 1,\,h^P_{1} = 1,\,h^P_{2} = 1,\,h^C_{1} = 1$ and $h^C_{2}=0.$ The decision problem can be stated as follows: “Does there exist a production schedule, $\nu=\{x_{ij},\, y_{ij},\, s_{ij}|i=1,\,2,\ldots, t+2;\, j=1,\,2\}$ such that the cost of the schedule $\Pi_{\nu} \leq D = (t+2)Mc_1 + (t+2)Mg_1 + [(t+2)M-B]u_2 + Bc_2 + Bg_2 + t\alpha = 2(t+2)M + B(M+1)+t\alpha?$”

Fig. 12

Inventory and purchasing decisions in ν

We let M = tα + 1 and α = B.

If part: suppose there exists a solution to the Partition problem. Let the solution be $\sum\nolimits_{a_k \in A_1} a_k = B$ and $\sum\nolimits_{a_j \in A_2} a_j = B,$ where A ₁ = A − A ₂. Note that the sequence of retailers is fixed: $(R_1,\, R_2\ldots, R_{t+2})$ and $I^C_{0j} = I^C_{t+2,j} = 0$ for j = 1, 2. We propose the production schedule ν as shown in Fig. 12 and Table 18. Table 19 calculates the cost for schedule $\nu:\, \Pi_{\nu} = D = 2(t+2)M+B(M+1)+t\alpha.$ This completes the proof for the If part. $\square$

Table 18 Production schedule ν

Table 19 The total cost calculation Π _ν

We list below the properties of the production schedule ν for facilitating the proof of the only if part.

• The demand of product P _j during each period is met by using no more than two different modes. That is, the administrative cost α _ij is 0 or α, for i = 1, 2,…, t + 2; j = 1, 2.

• M recovered units of product P ₂ are remanufactured during periods 1, 2,…, t + 1, and M − B units during period t + 2.

• All recovered units of product P ₁ are disposed during each period.

• There is no inventory carrying cost for component C ₁, since the demand for product P ₁ is satisfied by purchasing the new component C ₁ during each period.

• There is no inventory carrying cost for component C ₂, as $h^C_2=0.$

• There is no benefit in carrying inventories of recovered products P ₁ and P ₂; that is, $I_{ij}^P = 0,\, i =1,\, 2,\ldots, t+2;\, j=1,\, 2.$ due to the remanufacturer’s limited capacity.

Only If part: suppose there exists a production schedule, $\nu_o=\{x_{ij},\, y_{ij},\, s_{ij}|i=1,\,2,\ldots, t+2;\, j=1,\,2\}$ such that $\Pi_{\nu_o} \leq D= 2(t+2)M+B(M+1)+t\alpha.$ We now prove that there exists a Partition by establishing a number of claims.

We develop a lower bound L = 2(t + 1)M + B(M + 1) on the total cost of the production schedule ν _o .

Claim C1

$\Pi_{\nu_o} \geq L= 2(t+1)M+B(M+1).$

Proof

The lower bound L consists of three cost components, L = L ₁ + L ₂ + L ₃, and is estimated as follows.

• The total demand for product P ₁ during the planning horizon is (t + 2)M. The lower bound on the cost of satisfying the demand of product P ₁ is L ₁ = (t + 2)M, since the demand can be satisfied by either purchasing or remanufacturing component C ₁, as c ₁ = u ₁ = 1 and g ₁ = 0.

• The total demand for product P ₂ during the first t + 1 periods is (t + 1)M + B. The lower bound on the cost of satisfying the demand of product P ₂ during the first t + 1 periods is $L_2=(t+1)Mu_2+Bc_2=(t+1)M+BM+B,$ since c ₂ > u ₂ and the maximum remanufacturing capacity of P ₂ during the first t + 1 periods is (t + 1)M.

• The demand for product P ₂ during period t + 2 is M − B. Note that u ₂ = 1, g ₂ = 1, and c ₂ = tB + 2. The cost of satisfying the demand during period t + 2 therefore is minimized by remanufacturing M − B units and disposing of B units, as $I_{t+2,2}^C = 0.$ The lower bound on the cost of satisfying the demand of product P ₂ during period t + 2 is $L_3=(M-B)u_2+Bg_2=M.$

By adding all three costs, we obtain $\Pi_{\nu_o} \geq L= L_1+L_2+L_3=2(t+2)M + B(M+1).$ $\square$

Claim C2

In $\nu_o,\, I^P_{ij}=0,\, i = 1,\, 2, \ldots, t+2;\, j=1,\,2.$

Proof

Since $L_r = \mu\beta \frac{Q_0}{t+2}=M,$ where Q ₀ = Q ₁ = Q ₂ = (t + 2)M and μ = β = 1 from the construction, there is no advantage in carrying inventory of recovered products P ₁ and P ₂, that is, $I^P_{ij}=0,\,i = 1,\, 2, \ldots, t+2;\,j=1,\,2$ (see Theorem 2). $\square$

Claim C3

In ν _o , exactly B new units of component C ₂ must be purchased during periods 1, 2,…,t + 1.

Proof

Suppose B + θ new units of component C ₂ are purchased during period i, i = 1, 2,…,t + 1 where θ > 0. The lower bound on the cost of satisfying the demand of product P ₂, L ₂ + L ₃, can be revised as follows: $[(t+2)M-B-\theta]u_2 + (B+\theta) c_2 + B g_2 = (t+2)M + B(M+1)+ M\theta.$ From Claim C1, the lower bound on the cost of satisfying the demand of product P ₁ is L ₁ = (t + 2)M. Therefore, $\Pi_{\nu_o} \geq (t+2)M + B(M+1)+ M\theta + L_1 =2(t+2)M + B(M+1)+ M\theta = L + M\theta> D$ as θ > 0 and M = tα + 1. This contradicts the fact that $\Pi_{\nu_o} \leq D.$ Thus, θ = 0.

The total demand of product P ₂ during the first t + 1 periods is (t + 1)M + B. Since the maximum remanufacturing capacity of P ₂ during the first t + 1 periods is (t + 1)M, exactly B new units of component C ₂ must be purchased during period i, i = 1, 2,…,t + 1.$\square$

Claim C4

In $\nu_o,\,x^*_{i2}$ recovered units of product P ₂ must be remanufactured, where $x^*_{i2}=M,$ for i = 1, 2,…,t + 1, and $x^*_{i2}=M-B,$ for i = t + 2.

Proof

The total demand of product P ₂ during the first t + 1 periods is (t + 1)M + B. Since exactly B new units of component C ₂ are purchased during the first t + 1 periods (Claim C3), (t + 1)M units of component C ₂ must be remanufactured during those periods. Since the maximum remanufacturing capacity of product P ₂ during each period is $M,\,x^*_{i2}$ must be equal to M for i = 1, 2,…,t + 1.

The demand for component C ₂ during period t + 2 is M − B. Since u ₂ = 1, g ₂ = 1, and c ₂ = tB + 2, similar to the argument in Claim C1, the cost of satisfying the demand of product P ₂ during period t + 2 is minimized by remanufacturing M − B units and disposing of B units as $I_{t+2,2}^C = 0.$ Otherwise, $\Pi_{\nu_o} > D.$ Therefore, $x^*_{i2}=M-B$ for i = t + 2. $\square$

Claim C5

In ν _o ,  M recovered units of product P ₁ must be disposed during each period.

Proof

The result follows from Claims C2 and C4. $\square$

As a consequence of Claims C4 and C5, (t + 2)M new units of component C ₁ must be purchased (cost (t + 2)M c ₁ = (t + 2)M, as c ₁ = 1), and (t + 2)M recovered units of product P ₁ must be disposed (cost (t + 2)M g ₁ = 0 as g ₁ = 0). Since the demand for product P ₁ during each period is met by purchasing the original component C ₁, there is no administrative cost for satisfying the demand for product P ₁.

Claim C6

In ν _o , the demand for product P ₂ during each period must be satisfied by using no more than two modes, and the total administrative cost of fulfilling the demand of product P ₂ is tα.

Proof

M units of component C ₂ are remanufactured during period i, i = 1, 2,…,t + 1 (Claim C4). Remanufactured component C ₂ satisfies M − B units of demand for product P ₂ during the first period. Therefore, B remanufactured units of component C ₂ are carried over from the first period to the second period. Note that no administrative cost is incurred during period 1. However, since the demand for product P ₂ during period i, i = 2, 3,…,t + 1, is greater than M, we require at least one additional mode in order to fulfill the demand of product P ₂ during period i. This additional mode is either purchasing the new component C ₂ or using the remanufactured component C ₂ from inventory. During period t + 2, no administrative cost is incurred, since M − B units of demand for product P ₂ are met by the remanufactured component C ₂. The total administrative cost is therefore at least tα. If the demand for a period is satisfied by using three modes, then the additional administrative cost α is incurred. Therefore, $\Pi_{\nu_o} > L+ t\alpha + \alpha > D,$ contradicting the fact that $\Pi_{\nu_o} \leq D.$ The demand for product P ₂ must therefore be satisfied by using exactly two modes during periods 2, 3,…,t + 1. $\square$

Claim C7

$\sum\nolimits_{a_k \in A_1} a_k = B$ and $\sum\nolimits_{a_j \in A_2} a_j = B,$ where A ₁ = A − A ₂, and a solution to the Partition problem exists.

Proof

As a consequence of Claims C4 and C6, M units of demand for product P ₂ during periods 2, 3,…,t + 1, are satisfied by remanufactured components. The additional demand for product P ₂ beyond M in those periods corresponds to the elements in set $A=\{a_1,\, a_2, \ldots, a_{t-1}, a_t\},$ where $\sum\nolimits_{i=1}^t a_i = 2B.$ This additional demand in each period must be satisfied by a second mode (either the remanufactured components from inventory or purchased original components). Claim C3 implies that exactly B new units of component C ₂ are purchased. Therefore, B units of the additional demand must be satisfied by inventories carried from period 1. The remaining B units must be met by newly purchased units of component C ₂.

The demand for component C ₂ must be satisfied by using no more than two modes in each period (Claim C6). Consequently, the additional demand corresponding to subset $A_1 \subset A$ must use B remanufactured units of component C ₂ carried in inventory from period 1, and the remaining additional demand corresponding to the subset A ₂ = A − A ₁ must be met by using the new component C ₂. This implies that $\sum\nolimits_{a_k \in A_1} a_k = B$ and $\sum\nolimits_{a_j \in A_2} a_j = B,$ where $A_1 \subset A,\,A_2=A-A_1,$ and a solution to the Partition problem exists. $\square$

Claim C7 completes the proof of Theorem 5. $\square$