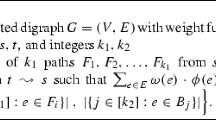Abstract
For a set \(W\) of vertices of a connected graph \(G=(V(G),E(G))\), a Steiner W-tree is a connected subgraph \(T\) of \(G\) such that \(W\subseteq V(T)\) and \(|E(T)|\) is minimum. Vertices in \(W\) are called terminals. In this work, we design an algorithm for the enumeration of all Steiner \(W\)-trees for a constant number of terminals, which is the usual scenario in many applications. We discuss algorithmic issues involving space requirements to compactly represent the optimal solutions and the time delay to generate them. After generating the first Steiner \(W\)-tree in polynomial time, our algorithm enumerates the remaining trees with \(O(n)\) delay (where \(n=|V(G)|\)). An algorithm to enumerate all Steiner trees was already known (Khachiyan et al., SIAM J Discret Math 19:966–984, 2005), but this is the first one achieving polynomial delay. A by-product of our algorithm is a representation of all (possibly exponentially many) optimal solutions using polynomially bounded space. We also deal with the following problem: given \(W\) and a vertex \(x\in V(G)\setminus W\), is \(x\) in a Steiner \(W'\)-tree for some \(\emptyset \ne W' \subseteq W\)? This problem is investigated from the complexity point of view. We prove that it is NP-hard when \(W\) has arbitrary size. In addition, we prove that deciding whether \(x\) is in some Steiner \(W\)-tree is NP-hard as well. We discuss how these problems can be used to define a notion of Steiner convexity in graphs.


Similar content being viewed by others
Notes
For the definition of incremental polynomial time, see Sect. 4.
References
Betzler, N. (2006). Steiner tree problems in the analysis of biological networks. Master Thesis, Tübingen University.
Björklund, A., Husfeldt, T., Kaski, P. & Koivisto, M. (2007). Fourier meets Möbious: Fast subset convolution. In Proceedings of STOC 2007 (pp. 67–74). New York: ACM Press.
Cayley, A. (1889). A theorem on trees. Quarterly Journal of Mathematics, 23, 376–378.
Cáceres, J., Márquez, A., & Puertas, M. L. (2008). Steiner distance and convexity in graphs. European Journal of Combinatorics, 29, 726–736.
Chartrand, G., Oellermann, O. R., Tian, S., & Zou, H. B. (1989). Steiner distance in graphs. Časopis pro pěstováni matematiky a fysiky, 114, 399–410.
Dourado, M. C., Oliveira, R. A., & Protti, F. (2009). Generating all the Steiner trees and computing Steiner intervals for a fixed number of terminals. In textitLAGOS’09—V Latin-American graphs, algorithms and optimization symposium, Gramado, Brazil, november 2009. Electronic notes in discrete mathematics (Vol. 35, pp. 323–328).
Dreyfus, S. E., & Wagner, R. A. (1972). The Steiner problem in graphs. Networks, 1, 195–207.
Eppstein, D. (1995). Representing all minimum spanning trees with applications to counting and generation. Technical Report 95–50, Department of Information and Computer Science, University of California, Irvine, CA. Available at http://www.ics.uci.edu/~eppstein/pubs/Epp-TR-95-50, Accessed 27 Feb 2014.
Fomin, F. V., Grandoni, F. & Kratsch, D. (2008). Faster Steiner tree computation in polynomial-space. In Proceedings of the 16th annual European symposium on algorithms, Karlsruhe, Germany. Lecture notes in computer science (Vol. 5193, pp. 430–441).
Fomin, F. V., Grandoni, F., Kratsch, D., Lokshtanov, D., & Saurabh, S. (2013). Computing optimal Steiner trees in polynomial space. Algorithmica, 65, 584–604.
Gilbert, E. N., & Pollack, H. O. (1968). Steiner minimal trees. SIAM Journal on Applied Mathematics, 16, 1–29.
Hakimi, S. L. (1971). Steiner’s problem in graph and its implications. Networks, 1, 113–133.
Hwang, F. K., Richards, D. C., & Winter, P. (1992). The Steiner tree problem. Amsterdam: North-Holland.
Karp, R. M. (1972). Reducibility among combinatorial problems. In R. E. Miller & J. W. Thatcher (Eds.), Complexity of computer computations (pp. 85–103). New York: Plenum.
Khachiyan, L., Boros, E., Elbassioni, K., Gurvich, V., & Makino, K. (2005). On the complexity of some enumeration problems for matroids. SIAM Journal on Discrete Mathematics, 19, 966–984.
Kimelfeld, B. & Sagiv, Y. (2005). Efficiently enumerating results of keyword search. In Proceedings of the 10th international symposium DBLP, Trondheim, Norway. Lecture notes in computer science (Vol. 3774, pp. 58–73)
Lauer, P. E., & Szwarcfiter, J. L. (1976). A search strategy for the elementary cycles of a directed graph. BIT Numerical Mathematics, 16, 192–204.
Lawler, E. L., Lenstra, J. K., & Rinnooy Kan, A. H. G. (1980). Generating all maximal independent sets: NP-hardness and polynomial time algorithms. SIAM Journal on Computing, 9, 558–565.
Levin, A. Y. (1971). Algorithm for shortest connection of a group of graph vertices. Soviet mathematics, Doklady, 12, 1477–1481.
Mölle, D., Richter, S., & Rossmanith, P. (2006). A faster algorithm for the Steiner tree problem. In Proceedings of STACS 2006 (pp. 561–570).
Nederlof, J. (2009). Fast polynomial-space algorithms using Möbius inversion: improving on Steiner tree and related problems. In Proceedings of ICALP 2009. Lecture notes in computer science (Vol. 5555, pp. 713–725).
Oellermann, O. R., & Puertas, M. L. (2007). Steiner intervals and Steiner geodetic numbers in distance-hereditary graphs. Discrete Mathematics, 307, 88–96.
Prömel, H. J., & Steger, A. (2002). The Steiner tree problem: A tour through graphs, algorithms and complexity. Advanced lectures in mathematics. Braunschweig: Vieweg.
Smith, J. M., & Toppur, B. (1996). Euclidean Steiner minimal trees, minimum energy configurations, and the embedding problem of weighted graphs in \(E^3\). Discrete Applied Mathematics, 71, 187–215.
Van de Vel, M. J. L. (1993). Theory of convex structures. Amsterdam: North-Holland.
Acknowledgments
This work is partially supported by CNPq and FAPERJ, Brazilian Research Agencies. We would like to express our gratitude to an anonymous referee that helped us very much to improve the presentation of this work.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Dourado, M.C., Oliveira, R.A. & Protti, F. Algorithmic aspects of Steiner convexity and enumeration of Steiner trees. Ann Oper Res 223, 155–171 (2014). https://doi.org/10.1007/s10479-014-1607-5
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10479-014-1607-5