Joint procurement and demand-side bidding strategies under price volatility

Abstract

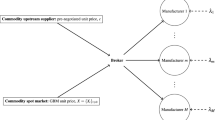
We consider a firm buying a commodity from a spot market as raw material and selling a final product by submitting bids. Bidding opportunities (i.e., demand arrivals) are random, and the likelihood of winning bids (i.e., selling the product) depends on the bid price. The price of the commodity raw material is also stochastic. The objective of the firm is to jointly decide on the procurement and bidding strategies to maximize its expected total discounted profit in the face of this demand and supply randomness. We model the commodity prices in the spot market as a Markov chain and the bidding opportunities as a Poisson process. Subsequently, we formulate the decision-making problem of the firm as an infinite-horizon stochastic dynamic program and analytically characterize its structural properties. We prove that the optimal procurement strategy follows a price-dependent base-stock policy and the optimal bidding price is decreasing with respect to the inventory level. We also formulate and analyze three intuitively appealing heuristic strategies, which either do not allow for carrying inventory or adopt simpler bidding policies (e.g., a constant bid price or myopically set bid prices). Using historical daily prices of several commodities, we then calibrate our models and conduct an extensive numerical study to compare the performances of the different strategies. Our study reveals the importance of adopting the optimal integrative procurement and bidding strategy, which is particularly rewarding when the raw material prices are more volatile and/or when there is significant competition on the demand side (the probability of winning is much smaller when submitting the same bid price). We establish that the relative performances of the three heuristic strategies depend critically on the holding cost of raw material inventory and the competitive environment, and identify conditions under which the shortfalls in profits from adopting such strategies are relatively less significant.

Appendices

Appendix 1: Proofs of Proposition 1 and Theorems 1 and 2

Proof of Proposition 1

In this proposition, we verify that the functional operators associated with MB, SB, and DB preserve Conditions 1 and 2 stated in Definition 1. Since the verification steps for MB and SB are very similar to those for DB, here, we only provide the proof for DB.

To simplify the proof, we rewrite $T_{\text{ DB }}$ as a linear combination of functional operators $G$ and $H$ as follows:

$$\begin{aligned} T_{\text{ DB }}v(x,i) = -h(x) + \lambda Gv(x,i) + \mu _i \sum _{j \ne i} \gamma _{ij} Hv(x,j) + (\overline{\mu } -\mu _i)v(x,i), \end{aligned}$$

where

$$\begin{aligned} Gv(x,i)= & {} \max _{b \ge 0} \biggl \{ (1-b)( Fv(x,i) + b)+ bv(x,i) \biggl \}, \\ Fv(x,i)= & {} \left\{ \begin{array}{ll} \max \bigl \{v(x,i)-p_i,v(x-1,i) \bigl \}, &{}\quad \text{ if }\,x \ge 1 \\ v(x,i) - p_{i}, &{}\quad \text{ if }\,x=0, \end{array} \right. \end{aligned}$$

and

$$\begin{aligned} Hv(x,j) = \max _{q \ge 0} \biggl \{ v(x+q,j)-p_j q \biggr \}. \end{aligned}$$

Now, we show that the functional operator $T_{\text{ DB }}$ preserves Conditions 1 and 2. We divide the proof into two steps, one for each condition. In each step, we consider $G$ and $H$ separately and show that Conditions 1 and 2 are preserved by each one of them.

Step 1. Verification of Condition 1.

Step 1.1. Preservation of Condition 1 by ${\mathbf {G}}$. We first focus on the concavity of $Gv(x,i)$ with respect to $x$.

If $x=0,$ we want to prove $Gv(2,i) - Gv(1,i) \le Gv(1,i) - Gv(0,i),$ that is, $\max _{b \ge 0} \bigl \{ (1-b) (\max \{v(2,i)-p_i,v(1,i) \} +b)+ bv(2,i) \bigl \} - \max _{b \ge 0} \bigl \{ (1-b) (\max \{v(1,i)-p_i,v(0,i) \} +b)+ bv(1,i) \bigl \} \,\,\le \max _{b \ge 0} \bigl \{ (1-b) (\max \{v(1,i)-p_i,v(0,i) \} +b)+ bv(1,i) \bigl \} - \max _{b \ge 0} \bigl \{ (1-b) (v(0,i)-p_i +b )+ bv(0,i) \bigl \}$. We consider the following four cases:

• Case A1. $v(2,i)-p_i \ge v(1,i)$ and $v(1,i)-p_i \ge v(0,i)$;

• Case A2. $v(2,i)-p_i \ge v(1,i)$ and $v(1,i)-p_i < v(0,i)$;

• Case A3. $v(2,i)-p_i < v(1,i)$ and $v(1,i)-p_i \ge v(0,i)$;

• Case A4. $v(2,i)-p_i < v(1,i)$ and $v(1,i)-p_i < v(0,i)$.

Case A1. $\Leftrightarrow \max _{b \ge 0} \bigl \{ (1-b) (v(2,i) +b -p_i )+ bv(2,i) \bigl \} - \max _{b \ge 0} \bigl \{ (1-b)( v(1,i) + b - p_i)+ bv(1,i) \bigl \}\,\le \max _{b \ge 0} \bigl \{ (1-b)( v(1,i) + b -p_i)+ bv(1,i) \bigl \} - \max _{b \ge 0} \bigl \{ (1-b)(v(0,i) + b -p_i)+ bv(0,i) \bigl \}.$ $\Leftrightarrow \max _{b \ge 0} \bigl \{ (1-b)(b-p_i)\bigl \} + v(2,i) -\max _{b \ge 0} \bigl \{ (1-b)(b-p_i) \bigl \} - v(1,i) \le \max _{b \ge 0} \bigl \{ (1-b)(b-p_i) \bigl \} + v(1,i) -\max _{b \ge 0} \bigl \{ (1-b)(b-p_i) \bigl \} - v(0,i).$ $\Leftrightarrow v(2,i) - v(1,i) \le v(1,i) - v(0,i).$

Case A2. This case is impossible since it contradicts with $v(2,i)-v(1,i) \le v(1,i)-v(0,i)$.

Case A3. $\Leftrightarrow \max _{b \ge 0} \bigl \{ (1-b)(v(1,i) +b)+ bv(2,i) \bigl \} - \max _{b \ge 0} \bigl \{ (1-b) ( v(1,i) + b - p_i)+ bv(1,i) \bigl \} \,\le \max _{b \ge 0} \bigl \{ (1-b) ( v(1,i) + b -p_i)+ bv(1,i) \bigl \} - \max _{b \ge 0} \bigl \{ (1-b) (v(0,i) + b - p_i) + b v(0,i)\bigl \}.$ $\Leftrightarrow \max _{b \ge 0} \bigl \{ (1-b)b -b(v(1,i) - v(2,i)) \bigl \} \,\le \max _{b \ge 0} \bigl \{ (1-b)(b -p_i) \bigl \} + v(1,i) - v(0,i).$ As for $\max _{b \ge 0} \bigl \{ (1-b)b -b(v(1,i) - v(2,i)) \bigl \}$, $b^{*}= \frac{1}{2}(1-(v(1,i)-v(2,i)))$ and $\max _{b \ge 0} \bigl \{ (1-b)b -b(v(1,i) - v(2,i)) \bigl \}= \frac{1}{4}(1-(v(1,i)-v(2,i)))^2$. As for $\max _{b \ge 0} \bigl \{ (1-b)(b -p_i) \bigl \}$, $b^{*}= \frac{1}{2}(1+p_i)$ and $\max _{b \ge 0} \bigl \{ (1-b)(b -p_i) \bigl \} = \frac{1}{4}(1-p_i)^2$. Hence, $\Leftrightarrow \frac{1}{4}(1-(v(1,i)-v(2,i)))^2 \le \frac{1}{4}(1-p_i)^2 + v(1,i) - v(0,i)$. Since $v(2,i) - v(1,i) < p_i$ and $1 + v(2,i) - v(1,i) \ge 1 - 1 = 0$, $\frac{1}{4}(1-(v(1,i)-v(2,i)))^2 = \frac{1}{4}(1+v(2,i)-v(1,i))^2 \le \frac{1}{4}(1+p_i)^2$. Moreover, $\frac{1}{4}(1-p_i)^2 + v(1,i) - v(0,i) \ge \frac{1}{4}(1-p_i)^2 + p_i = \frac{1}{4}(1 + p_i)^2.$

Case A4. $\Leftrightarrow \max _{b \ge 0} \bigl \{ (1-b) (v(1,i) +b)+ bv(2,i) \bigl \} - \max _{b \ge 0} \bigl \{ (1-b) ( v(0,i) + b ) + bv(1,i) \bigl \}\, \le \max _{b \ge 0} \bigl \{ (1-b) ( v(0,i) + b)+ bv(1,i) \bigl \} - \max _{b \ge 0} \bigl \{ (1-b) (v(0,i) + b - p_i) + b v(0,i)\bigl \}.$ $\Leftrightarrow \max _{b \ge 0} \bigl \{ (1-b)b - b (v(1,i) - v(2,i)) \bigl \} - \max _{b \ge 0} \bigl \{ (1-b)b - b( v(0,i) - v(1,i)) \bigl \} - (v(0,i)-v(1,i)) \,\le \max _{b \ge 0} \bigl \{ (1-b)b - b( v(0,i) - v(1,i)) \bigl \} - \max _{b \ge 0} \bigl \{ (1-b)(b -p_i) \bigl \}.$ $\Leftrightarrow \frac{1}{4}(1-(v(1,i)-v(2,i)))^2 - \frac{1}{4}(1-(v(0,i)-v(1,i)))^2 - (v(0,i)-v(1,i)) \le \frac{1}{4}(1-(v(0,i)-v(1,i)))^2 - \frac{1}{4}(1 - p_i)^2.$ $\Leftrightarrow (1-(v(1,i)-v(2,i)))^2 - (1 + v(0,i)-v(1,i))^2 \le (1+v(1,i)-v(0,i))^2 - (1 - p_i)^2.$ Since $v(2,i)-v(1,i) \le v(1,i)-v(0,i)$, $1+v(2,i)-v(1,i) \ge 1-1=0,$ and $1+v(1,i)-v(0,i) \ge 1- 1 = 0,$ we have $(1-(v(1,i)-v(2,i)))^2 \le (1+v(1,i)-v(0,i))^2.$ Moreover, since $v(0,i)-v(1,i) > -p_i,$ we have $1+v(0,i)-v(1,i)>1 - p_i \ge 0.$ Then, we have $(1 + v(0,i)-v(1,i))^2 > (1 - p_i)^2.$

If $x \ge 1,$ we want to prove $Gv(x+2,i) - Gv(x+1,i) \le Gv(x+1,i) - Gv(x,i),$ that is, $\max _{b \ge 0} \bigl \{ (1-b) (\max \{v(x+2,i)-p_i,v(x+1,i) \} +b )+ bv(x+2,i) \bigl \} - \max _{b \ge 0} \bigl \{ (1-b) (\max \{v(x+1,i)-p_i,v(x,i) \} +b)+ bv(x+1,i) \bigl \} \,\le \max _{b \ge 0} \bigl \{ (1-b) (\max \{v(x+1,i)-p_i,v(x,i) \} +b)+ bv(x+1,i) \bigl \} - \max _{b \ge 0} \bigl \{ (1-b) (\max \{v(x,i)-p_i,v(x-1,i) \} +b) + bv(x,i) \bigl \}.$ Since $v(x,i)$ is concave with respect to $x$, there exists an integer $x^*$ such that if $x \le x^*$, $v(x,i)-p_i \ge v(x-1,i)$ and if $x > x^*,$ $v(x,i) - p_i < v(x-1,i)$. We consider the following four cases:

• Case B1. $x \le x^* -2$;

• Case B2. $x = x^* -1$;

• Case B3. $x = x^*$;

• Case B4. $x \ge x^* + 1$.

Case B1. $\max _{b \ge 0} \bigl \{ (1-b) (v(x+2,i) +b - p_i)+ bv(x+2,i) \bigl \} - \max _{b \ge 0} \bigl \{ (1-b) ( v(x+1,i) + b - p_i )+ bv(x+1,i) \bigl \} \,\le \max _{b \ge 0} \bigl \{ (1-b)( v(x+1,i) + b -p_i )+ bv(x+1,i) \bigl \} - \max _{b \ge 0} \bigl \{ (1-b) (v(x,i) + b - p_i ) + b v(x,i) \bigl \}.$ $\Leftrightarrow \max _{b \ge 0} \bigl \{ (1-b)(b-p_i) \bigl \} + v(x+2,i) - \max _{b \ge 0} \bigl \{ (1-b)(b-p_i) \bigl \} - v(x+1,i) \le \max _{b \ge 0} \bigl \{ (1-b)(b-p_i) \bigl \} + v(x+1,i) - \max _{b \ge 0} \bigl \{ (1-b)(b-p_i) \bigl \} - v(x,i).$ $\Leftrightarrow v(x+2,i) - v(x+1,i) \le v(x+1,i) - v(x,i).$

Case B2. $\max _{b \ge 0} \bigl \{ (1-b)(v(x+1,i) +b)+ bv(x+2,i) \bigl \} - \max _{b \ge 0} \bigl \{ (1-b)( v(x+1,i) + b - p_i)+ bv(x+1,i) \bigl \} \,\,\le \max _{b \ge 0} \bigl \{ (1-b) ( v(x+1,i) + b -p_i )+ bv(x+1,i) \bigl \} - \max _{b \ge 0} \bigl \{ (1-b)(v(x,i) + b - p_i ) + b v(x,i)\bigl \}.$ $\Leftrightarrow \max _{b \ge 0} \bigl \{ (1-b)b -b(v(x+1,i) - v(x+2,i)) \bigl \} - \max _{b \ge 0} \bigl \{ (1-b)(b - p_i) \bigl \}\,\, \le v(x+1,i) - v(x,i).$ $\Leftrightarrow \frac{1}{4}(1-(v(x+1,i)-v(x+2,i)))^2 - \frac{1}{4}(1-p_i)^2 \le v(x+1,i) - v(x,i).$ Since $x+2 = x^*-1+2=x^*+1 > x^*,$ we have $v(x+2,i)-v(x+1,i) <p_i.$ So, $1-(v(x+1,i)-v(x+2,i)) = 1 + v(x+2,i)-v(x+1,i) < 1+p_i.$ Combining with the fact that $1-(v(x+1,i)-v(x+2,i)) = 1 + v(x+2,i)-v(x+1,i) \ge 1 - 1 = 0,$ we have $\frac{1}{4}(1-(v(x+1,i)-v(x+2,i)))^2 - \frac{1}{4}(1-p_i)^2 \le \frac{1}{4}(1+p_i)^2 - \frac{1}{4}(1-p_i)^2 = p_i.$ Moreover, since $x=x^*-1,$ that is, $x+1=x^*,$ we have $v(x+1,i)-p_i \ge v(x,i).$ Hence, $v(x+1,i)-v(x,i) \ge p_i.$

Case B3. $\max _{b \ge 0} \bigl \{ (1-b) (v(x+1,i) +b)+ bv(x+2,i) \bigl \} - \max _{b \ge 0} \bigl \{ (1-b) ( v(x,i) + b )+ bv(x+1,i) \bigl \} \,\le \max _{b \ge 0} \bigl \{ (1-b) ( v(x,i) + b )+ bv(x+1,i) \bigl \} - \max _{b \ge 0} \bigl \{ (1-b) (v(x,i) + b - p_i ) + b v(x,i)\bigl \}.$ $\Leftrightarrow \max _{b \ge 0} \bigl \{ (1-b)b - b(v(x+1,i) - v(x+2,i) ) \bigl \} - \max _{b \ge 0} \bigl \{ (1-b)b - b(v(x,i) - v(x+1,i)) \bigl \} - (v(x,i) - v(x+1,i)) \le \max _{b \ge 0} \bigl \{ (1-b)b - b(v(x,i) - v(x+1,i)) \bigl \} - \max _{b \ge 0} \bigl \{ (1-b)(b - p_i) \bigl \}.$ $\Leftrightarrow \frac{1}{4}(1-(v(x+1,i)-v(x+2,i)))^2 - \frac{1}{4}(1-(v(x,i)-v(x+1,i)))^2 - (v(x,i) - v(x+1,i)) \le \frac{1}{4}(1-(v(x,i)-v(x+1,i)))^2 - \frac{1}{4}(1-p_i)^2.$ $\Leftrightarrow (1+v(x+2,i)-v(x+1,i))^2 - (1+v(x,i)-v(x+1,i))^2 \le (1+v(x+1,i)-v(x,i))^2 - (1-p_i)^2.$ Since $v(x+2,i)-v(x+1,i) \le v(x+1,i) - v(x,i)$, $1+v(x+2,i)-v(x+1,i) \ge 1 - 1 = 0,$ and $1+v(x+1,i)-v(x,i) \ge 1 - 1 = 0,$ we have $(1+v(x+2,i)-v(x+1,i))^2 \le (1+v(x+1,i)-v(x,i))^2.$ Moreover, since $v(x+1,i) - v(x,i) < p_i,$ we have $v(x,i) - v(x+1,i) > -p_i.$ Combining with the fact that $1 + v(x,i) - v(x+1,i) \ge 1 - p_i \ge 0$, we have $(1+v(x,i)-v(x+1,i))^2 \ge (1-p_i)^2.$

Case B4. $\Leftrightarrow \max _{b \ge 0} \bigl \{ (1-b) (v(x+1,i) +b)+ bv(x+2,i) \bigl \} - \max _{b \ge 0} \bigl \{ (1-b)( v(x,i) + b)+ bv(x+1,i) \bigl \} \, \le \max _{b \ge 0} \bigl \{ (1-b)( v(x,i) + b)+ bv(x+1,i) \bigl \} - \max _{b \ge 0} \bigl \{ (1-b) (v(x-1,i) + b) + b v(x,i)\bigl \}.$ $\Leftrightarrow \max _{b \ge 0} \bigl \{ (1-b)b - b(v(x+1,i) - v(x+2,i)) \bigl \} - \max _{b \ge 0} \bigl \{ (1-b)b - b(v(x,i) - v(x+1,i)) \bigl \} -(v(x,i) - v(x+1,i)) \le \max _{b \ge 0} \bigl \{ (1-b)b - b(v(x,i) - v(x+1,i)) \bigl \} - \max _{b \ge 0} \bigl \{ (1-b)b - b(v(x-1,i) - v(x,i)) \bigl \}-(v(x-1,i) - v(x,i)).$ $\Leftrightarrow \frac{1}{4}(1-(v(x+1,i)-v(x+2,i)))^2 - \frac{1}{4}(1-(v(x,i)-v(x+1,i)))^2 - (v(x,i) - v(x+1,i)) \le \frac{1}{4}(1-(v(x,i)-v(x+1,i)))^2 - \frac{1}{4}(1-(v(x-1,i)-v(x,i)))^2 - (v(x-1,i) - v(x,i)).$ $\Leftrightarrow (1+v(x+2,i)-v(x+1,i))^2 - (1+v(x,i)-v(x+1,i))^2 \le (1+v(x+1,i)-v(x,i))^2 - (1+v(x-1,i)-v(x,i))^2.$ Since $v(x+2,i) -v(x+1,i) \le v(x+1,i) - v(x,i),$ $1+v(x+2,i)-v(x+1,i) \ge 1-1 = 0,$ and $1+v(x+1,i)-v(x,i) \ge 1-1= 0,$ we have $(1+v(x+2,i)-v(x+1,i))^2 \le (1+v(x+1,i)-v(x,i))^2.$ Moreover, since $v(x+1,i)-v(x,i) \le v(x,i)-v(x-1,i),$ we have $v(x,i)-v(x+1,i) \ge v(x-1,i)-v(x,i).$ Combining with the facts that $1+v(x,i)-v(x+1,i) \ge 0$ (since $v(x+1,i)-p_i < v(x,i),$ we have $v(x,i)-v(x+1,i) > -p_i.$ So, $1+v(x,i)-v(x+1,i) > 1- p_i \ge 0$) and $1+v(x-1,i)-v(x,i) \ge 0$ (since $v(x,i)-p_i < v(x-1,i),$ we have $v(x-1,i)-v(x,i) > -p_i.$ So, $1+v(x-1,i)-v(x,i) > 1- p_i \ge 0$), we have $(1+v(x,i)-v(x+1,i))^2 \ge (1+v(x-1,i)-v(x,i))^2.$

Step 1.2. Preservation of Condition 1 by ${\mathbf {H}}$. Now, we focus on the concavity of $Hv(x,j)$ with respect to $x$. Define

$$\begin{aligned} \tilde{H}v(x,j) = \max _{y \ge x} \bigl \{ v(y,j) - p_j y \bigl \}. \end{aligned}$$

So, $Hv(x,j) = \tilde{H}v(x,j) + p_j x.$ Since $p_j x$ is linear in $x$, we focus on the concavity of $\tilde{H}v(x,j)$ with respect to $x$, that is, we want to prove $\tilde{H}v(x+2,j)-\tilde{H}v(x+1,j) \le \tilde{H}v(x+1,j)-\tilde{H}v(x,j).$ Let $y^*$ be an integer such that $y^* = \arg \max _{y=0,1,\ldots } \bigl \{ v(y,j) -p_j y \bigl \}.$ Then, from the concavity of $v(x,j)$ with respect to $x$, we have

$$\begin{aligned} \tilde{H}v(x,j) = \left\{ \begin{array}{ll} v(y^*,j)-p_{j} y^*, &{}\quad \text{ if }\,y^* > x \\ v(x,j) - p_{j}x, &{}\quad \text{ if }\,y^* \le x. \end{array} \right. \end{aligned}$$

We consider the following three cases:

• Case C1. $x \le y^* -2$;

• Case C2. $x = y^* -1$;

• Case C3. $x \ge y^*$.

Case C1. $\tilde{H}v(x+2,j)-\tilde{H}v(x+1,j) = v(y^*,j)-p_j y^* - (v(y^*,j)-p_j y^*) = 0 = \tilde{H}v(x+1,j)-\tilde{H}v(x,j).$

Case C2. $\tilde{H}v(x+2,j)-\tilde{H}v(x+1,j) = v(y^*+1,j)-p_j (y^*+1) - (v(y^*,j)-p_j y^*) \le 0.$ The last inequality follows because of the optimality of $y^*.$ Moreover, $\tilde{H}v(x+1,j)-\tilde{H}v(x,j) = v(y^*,j)-p_j y^* - (v(y^*,j)-p_j y^*) = 0.$ Hence, $\tilde{H}v(x+2,j)-\tilde{H}v(x+1,j) \le \tilde{H}v(x+1,j)-\tilde{H}v(x,j).$

Case C3. $\tilde{H}v(x+2,j)-\tilde{H}v(x+1,j) = v(x+2,j)-p_j (x+2) - (v(x+1,j)-p_j(x+1)) = v(x+2,j) - v(x+1,j) - p_j.$ $\tilde{H}v(x+1,j)-\tilde{H}v(x,j) = v(x+1,j)-p_j (x+1) - (v(x,j)-p_jx) = v(x+1,j) - v(x,j) - p_j.$ Since $v(x+2,j) - v(x+1,j) \le v(x+1,j) - v(x,j),$ we have $\tilde{H}v(x+2,j)-\tilde{H}v(x+1,j) \le \tilde{H}v(x+1,j)-\tilde{H}v(x,j).$

Step 1.3. Preservation of Condition 1 by ${\mathbf {T}}_{\text{ DB }}$. Summarizing the above results and observing that $-h(x)$ is concave, we conclude that $T_{\text{ DB }}$ preserves Condition 1, since it is the linear combination of terms that satisfy Condition 1.

Step 2. Verification of Condition 2.

Step 2.1. Preservation of Condition 2 by ${\mathbf {G}}$. First, we focus on $Gv(x,i).$ We want to prove $Gv(x+1,i)-Gv(x,i) \ge -1$ for $x \in N$ and $i \in M$.

If $x=0$, $Gv(1,i)-Gv(0,i) = \max _{b \ge 0} \bigl \{ (1-b) (\max \{v(1,i)-p_i,v(0,i) \} +b)+ bv(1,i) \bigl \} - \max _{b \ge 0} \bigl \{ (1-b)(b-p_i) \bigl \} - v(0,i).$ We consider the following two cases:

• Case D1. $v(1,i) - p_i \ge v(0,i)$;

• Case D2. $v(1,i) - p_i < v(0,i)$.

Case D1. $Gv(1,i)-Gv(0,i) = \max _{b \ge 0} \bigl \{ (1-b) (v(1,i) + b - p_i) + bv(1,i) \bigl \} - \max _{b \ge 0} \bigl \{ (1-b)(b-p_i) \bigl \} - v(0,i) = v(1,i) - v(0,i) \ge -1.$

Case D2. $Gv(1,i)-Gv(0,i) = \max _{b \ge 0} \bigl \{ (1-b) ( v(0,i) + b ) + bv(1,i) \bigl \} - \max _{b \ge 0} \bigl \{ (1-b)(b-p_i) \bigl \} - v(0,i) = \frac{1}{4}(1-(v(0,i)-v(1,i)))^2 - \frac{1}{4}(1-p_i)^2.$ Since $v(1,i) - v(0,i) \ge -1,$ we have $1-(v(0,i) - v(1,i)) = 1 +v(1,i) - v(0,i) \ge 1-1 = 0.$ Hence, $\frac{1}{4}(1-(v(0,i)-v(1,i)))^2 - \frac{1}{4}(1-p_i)^2 \ge 0 - \frac{1}{4}(1-p_i)^2 = - \frac{1}{4}(1-p_i)^2 \ge -1.$

If $x \ge 1,$ we consider the following three cases:

• Case E1. $x \le x^* -1$;

• Case E2. $x = x^*$;

• Case E3. $x \ge x^* + 1$.

Case E1. $Gv(x+1,i)-Gv(x,i) = \max _{b \ge 0} \bigl \{ (1-b) ( v(x+1,i) + b -p_i)+ bv(x+1,i) \bigl \} - \max _{b \ge 0} \bigl \{ (1-b) ( v(x,i) + b -p_i) + bv(x,i) \bigl \} = v(x+1,i) - v(x,i) \ge - 1.$

Case E2. $Gv(x+1,i)-Gv(x,i) = \max _{b \ge 0} \bigl \{ (1-b) ( v(x,i) + b) + bv(x+1,i) \bigl \} - \max _{b \ge 0} \bigl \{ (1-b) ( v(x,i) + b -p_i) + bv(x,i) \bigl \} = \frac{1}{4}(1-(v(x,i)-v(x+1,i)))^2 - \frac{1}{4}(1-p_i)^2.$ Since $v(x+1,i) - v(x,i) \ge -1,$ we have $1-(v(x,i) - v(x+1,i)) = 1 +v(x+1,i) - v(x,i) \ge 1-1=0.$ Hence, $\frac{1}{4}(1-(v(x,i)-v(x+1,i)))^2 - \frac{1}{4}(1-p_i)^2 \ge 0 - \frac{1}{4}(1-p_i)^2 = - \frac{1}{4}(1-p_i)^2 \ge -1.$

Case E3. $Gv(x+1,i)-Gv(x,i) = \max _{b \ge 0} \bigl \{ (1-b) ( v(x,i) + b) + bv(x+1,i) \bigl \} - \max _{b \ge 0} \bigl \{ (1-b) ( v(x-1,i) + b ) + bv(x,i) \bigl \}\, =\frac{1}{4}(1-(v(x,i)-v(x+1,i)))^2 - \frac{1}{4}(1-(v(x-1,i)-v(x,i)))^2 - (v(x-1,i) - v(x,i))=\frac{1}{4}(1-(v(x,i)-v(x+1,i)))^2 - \frac{1}{4}(1+v(x-1,i)-v(x,i))^2.$ Since $v(x+1,i)-v(x,i) \ge -1,$ we have $1+v(x+1,i)-v(x,i) \ge 1- 1 = 0.$ Hence, $\frac{1}{4}(1-(v(x,i)-v(x+1,i)))^2 = \frac{1}{4}(1+v(x+1,i)-v(x,i))^2 \ge 0.$ Moreover, since $v(x+1,i)-v(x,i) \ge -1$ and $v(x+1,i)-v(x,i) \le v(x,i) - v(x-1,i),$ we have $v(x,i)-v(x-1,i) \ge -1,$ that is, $v(x-1,i)-v(x,i) \le 1.$ Since $0 \le 1-p_i \le 1 + v(x-1,i)-v(x,i) \le 1+1 =2,$ we have $\frac{1}{4}(1+v(x-1,i)-v(x,i))^2 \le \frac{1}{4} \times 2^2 = 1.$ Hence, $Gv(x+1,i)-Gv(x,i) \ge 0 - 1 = -1.$

Step 2.2. Preservation of Condition 2 by ${\mathbf {H}}$. Here, we focus on $Hv(x,j).$ We want to prove $Hv(x+1,j)-Hv(x,j) \ge -1$ for $x \in N$ and $i \in M$. We consider the following two cases:

• Case F1. $x \le y^* -1$;

• Case F2. $x \ge y^*$.

Case F1. $Hv(x+1,j)-Hv(x,j) = v(y^*,j) - p_jy^* + p_j(x+1)-(v(y^*,j) - p_jy^* + p_jx) = p_j \ge -1.$

Case F2. $Hv(x+1,j)-Hv(x,j) = v(x+1,j) - p_j(x+1) + p_j(x+1)-(v(x,j) - p_jx + p_jx) = v(x+1,j) -v(x,j) \ge -1.$

Step 2.3. Preservation of Condition 2 by ${\mathbf {T}}_{\text{ DB }}$. In conclusion,

$$\begin{aligned} T_{\text{ DB }}v(x+1,i) - T_{\text{ DB }}v(x,i)\ge & {} -h(x+1)-(-h(x)) + \lambda (-1) \\&+ \mu _i \sum _{j \ne i} \gamma _{ij} (-1) + (\overline{\mu }-\mu _i)(-1) \\= & {} -(h(x+1)-h(x)) + (\lambda + \overline{\mu })(-1) \\\ge & {} - \alpha + (\lambda + \overline{\mu })(-1) = (\alpha + \lambda + \overline{\mu })(-1) = -1. \end{aligned}$$

Proof of Theorem 1

Since the results follow from the concavity of $V_{\text{ I }}$, we only need to prove $V_{\text{ I }} \in {\mathcal {V}}.$ This can be easily shown by using the facts that (i) $V_{\text{ I }} = \lim _{n \rightarrow \infty } T^n_{\text{ I }} v$ for any $v$ in ${\mathcal {V}}$, where $T^n_{\text{ I }}$ is the $n$-fold composition of $T_{\text{ I }}$ for $\text{ I } \in \{\text{ MB, } \text{ SB, } \text{ DB }\}$ and (ii) $V_{\text{ I }}$ is the unique solution of $v = T_{\text{ I }}v$ (see Theorem 5.1 of Porteus 1982 and Theorem 6.10.4 of Puterman 1994).

Proof of Theorem 2

Recall that

$$\begin{aligned} T_{\text{ DB }}v(x,i) = -h(x) + \lambda Gv(x,i) + \mu _i \sum _{j \ne i} \gamma _{ij} Hv(x,j) + (\overline{\mu } -\mu _i)v(x,i), \end{aligned}$$

where

$$\begin{aligned} Gv(x,i)= & {} \max _{b \ge 0} \biggl \{ (1-b)( Fv(x,i) + b)+ bv(x,i) \biggl \}, \\ Fv(x,i)= & {} \left\{ \begin{array}{ll} \max \bigl \{v(x,i)-p_i,v(x-1,i) \bigl \}, &{}\quad \text{ if }\, x \ge 1 \\ v(x,i) - p_{i}, &{}\quad \text{ if }\, x=0, \end{array} \right. \end{aligned}$$

and

$$\begin{aligned} Hv(x,j) = \max _{q \ge 0} \biggl \{ v(x+q,j)-p_j q \biggr \}. \end{aligned}$$

Note that the optimal bid prices are determined by the maximization of $(1-b)(FV_{\text{ DB }}(x,i) +b)+ bV_{\text{ DB }}(x,i)$ with respect to $b$. Let $Z(b,x) = (1-b)(FV_{\text{ DB }}(x,i) +b)+ bV_{\text{ DB }}(x,i)$. To prove the monotonicity of the optimal bid prices with respect to the inventory level, it suffices to show $Z(b^{'},x+1)-Z(b^{'},x) \le Z(b,x+1) - Z(b,x)$ for all $x \ge 0$ and $1 \ge b^{'} \ge b \ge 0.$

If $x=0,$ we want to prove $Z(b^{'},1)-Z(b^{'},0) \le Z(b,1) - Z(b,0)$, that is, $(1-b^{'})(FV_{\text{ DB }}(1,i)+b^{'}) + b^{'}V_{\text{ DB }}(1,i) - (1-b^{'})(FV_{\text{ DB }}(0,i)+b^{'}) - b^{'}V_{\text{ DB }}(0,i) \le (1-b)(FV_{\text{ DB }}(1,i)+b) + bV_{\text{ DB }}(1,i) - (1-b)(FV_{\text{ DB }}(0,i)+b) - bV_{\text{ DB }}(0,i).$ We consider the following two cases:

• Case G1. $V_{\text{ DB }}(1,i)-p_i \ge V_{\text{ DB }}(0,i)$;

• Case G2. $V_{\text{ DB }}(1,i)-p_i < V_{\text{ DB }}(0,i)$.

Case G1. $\Leftrightarrow (1-b^{'})(V_{\text{ DB }}(1,i) - p_i + b^{'}) + b^{'}V_{\text{ DB }}(1,i) - (1-b^{'})(V_{\text{ DB }}(0,i)-p_i+b^{'}) - b^{'}V_{\text{ DB }}(0,i) \le (1-b)(V_{\text{ DB }}(1,i) - p_i + b) + bV_{\text{ DB }}(1,i) - (1-b)(V_{\text{ DB }}(0,i)-p_i+b) - bV_{\text{ DB }}(0,i).$ $\Leftrightarrow V_{\text{ DB }}(1,i) - V_{\text{ DB }}(0,i) \le V_{\text{ DB }}(1,i) - V_{\text{ DB }}(0,i).$

Case G2. $\Leftrightarrow (1-b^{'})(V_{\text{ DB }}(0,i) + b^{'}) + b^{'}V_{\text{ DB }}(1,i) - (1-b^{'})(V_{\text{ DB }}(0,i)-p_i+b^{'}) - b^{'}V_{\text{ DB }}(0,i) \le (1-b)(V_{\text{ DB }}(0,i) + b) + bV_{\text{ DB }}(1,i) - (1-b)(V_{\text{ DB }}(0,i)-p_i+b) - bV_{\text{ DB }}(0,i).$ $\Leftrightarrow b^{'}(V_{\text{ DB }}(1,i)-V_{\text{ DB }}(0,i)-p_i) + p_i \le b(V_{\text{ DB }}(1,i)-V_{\text{ DB }}(0,i)-p_i) + p_i.$ $\Leftrightarrow b^{'} \ge b.$

If $x \ge 1,$ we want to prove $Z(b^{'},x+1)-Z(b^{'},x) \le Z(b,x+1) - Z(b,x)$, that is, $(1-b^{'})(FV_{\text{ DB }}(x+1,i)+b^{'}) + b^{'}V_{\text{ DB }}(x+1,i) - (1-b^{'})(FV_{\text{ DB }}(x,i)+b^{'}) - b^{'}V_{\text{ DB }}(x,i) \le (1-b)(FV_{\text{ DB }}(x+1,i)+b) + bV_{\text{ DB }}(x+1,i) - (1-b)(FV_{\text{ DB }}(x,i)+b) - bV_{\text{ DB }}(x,i).$ From the proof of Theorem 1, $V_{\text{ DB }}(x,i)$ is concave with respect to $x$. Hence, there exists an integer $x^{*}$ such that for $x \ge 1,$

$$\begin{aligned} FV_{\text{ DB }}(x,i) = \left\{ \begin{array}{ll} V_{\text{ DB }}(x,i)-p_i, &{}\quad \text{ if }\,x \le x^{*} \\ V_{\text{ DB }}(x-1,i), &{}\quad \text{ if }\,x > x^{*}. \end{array} \right. \end{aligned}$$

We consider the following three cases:

• Case H1. $x \le x^{*}-1$;

• Case H2. $x = x^{*}$;

• Case H3. $x \ge x^{*}+1.$

Case H1. $\Leftrightarrow (1-b^{'})(V_{\text{ DB }}(x+1,i) - p_i +b^{'}) + b^{'}V_{\text{ DB }}(x+1,i) - (1-b^{'})(V_{\text{ DB }}(x,i) -p_i + b^{'}) - b^{'}V_{\text{ DB }}(x,i) \le (1-b)(V_{\text{ DB }}(x+1,i)- p_i +b) + bV_{\text{ DB }}(x+1,i) - (1-b)(V_{\text{ DB }}(x,i) - p_i +b) - bV_{\text{ DB }}(x,i).$ $\Leftrightarrow V_{\text{ DB }}(x+1,i) - V_{\text{ DB }}(x,i) \le V_{\text{ DB }}(x+1,i) - V_{\text{ DB }}(x,i).$

Case H2. $\Leftrightarrow (1-b^{'})(V_{\text{ DB }}(x,i)+b^{'}) + b^{'}V_{\text{ DB }}(x+1,i) - (1-b^{'})(V_{\text{ DB }}(x,i) -p_i + b^{'}) - b^{'}V_{\text{ DB }}(x,i) \le (1-b)(V_{\text{ DB }}(x,i)+b) + bV_{\text{ DB }}(x+1,i) - (1-b)(V_{\text{ DB }}(x,i) - p_i +b) - bV_{\text{ DB }}(x,i).$ $\Leftrightarrow b^{'}(V_{\text{ DB }}(x+1,i)-V_{\text{ DB }}(x,i)) + (1-b^{'})p_i \le b(V_{\text{ DB }}(x+1,i)-V_{\text{ DB }}(x,i)) + (1-b)p_i.$ $\Leftrightarrow b^{'}(V_{\text{ DB }}(x+1,i)-V_{\text{ DB }}(x,i)-p_i) \le b(V_{\text{ DB }}(x+1,i)-V_{\text{ DB }}(x,i) - p_i).$ Since $x+1=x^{*}+1 > x^{*},$ we have $V_{\text{ DB }}(x+1,i)-V_{\text{ DB }}(x,i)-p_i < 0.$ Hence, $\Leftrightarrow b^{'} \ge b.$

Case H3. $\Leftrightarrow (1-b^{'})(V_{\text{ DB }}(x,i)+b^{'}) + b^{'}V_{\text{ DB }}(x+1,i) - (1-b^{'})(V_{\text{ DB }}(x-1,i) + b^{'}) - b^{'}V_{\text{ DB }}(x,i) \le (1-b)(V_{\text{ DB }}(x,i)+b) + bV_{\text{ DB }}(x+1,i) - (1-b)(V_{\text{ DB }}(x-1,i)+b) - bV_{\text{ DB }}(x,i).$ $\Leftrightarrow V_{\text{ DB }}(x,i) - V_{\text{ DB }}(x-1,i) + b^{'}(V_{\text{ DB }}(x-1,i) - V_{\text{ DB }}(x,i) - V_{\text{ DB }}(x,i) + V_{\text{ DB }}(x+1,i)) \le V_{\text{ DB }}(x,i) - V_{\text{ DB }}(x-1,i) + b(V_{\text{ DB }}(x-1,i) - V_{\text{ DB }}(x,i) - V_{\text{ DB }}(x,i) + V_{\text{ DB }}(x+1,i)).$ $\Leftrightarrow b^{'}(V_{\text{ DB }}(x-1,i) - V_{\text{ DB }}(x,i) - V_{\text{ DB }}(x,i) + V_{\text{ DB }}(x+1,i)) \le b(V_{\text{ DB }}(x-1,i) - V_{\text{ DB }}(x,i) - V_{\text{ DB }}(x,i) + V_{\text{ DB }}(x+1,i)).$ From the proof of Theorem 1, $V_{\text{ DB }}(x,i)$ is concave with respect to $x$, that is, $V_{\text{ DB }}(x+1,i)-V_{\text{ DB }}(x,i) \le V_{\text{ DB }}(x,i) - V_{\text{ DB }}(x-1,i).$ So, $V_{\text{ DB }}(x-1,i) - V_{\text{ DB }}(x,i) - V_{\text{ DB }}(x,i) + V_{\text{ DB }}(x+1,i) \le 0.$ Hence, $\Leftrightarrow b^{'} \ge b.$

Appendix 2. Tables for the other commodities: food index, oil, and platinum

See Tables 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, and 18

Table 7 Average profit rate comparison results for all strategies: food index

Table 8 Average profit rate comparison results for all strategies: oil

Table 9 Average profit rate comparison results for all strategies: platinum

Table 10 Base-stock levels comparison results for MB, SB, and DB strategies: food index

Table 11 Base-stock levels comparison results for MB, SB, and DB strategies: oil

Table 12 Base-stock levels comparison results for MB, SB, and DB strategies: platinum

Table 13 Average bid price and average inventory comparison results for all strategies: food index

Table 14 Average bid price and average inventory comparison results for all strategies: oil

Table 15 Average bid price and average inventory comparison results for all strategies: platinum

Table 16 Average total profit comparison results for all strategies using real data: food index

Table 17 Average total profit comparison results for all strategies using real data: oil

Table 18 Average total profit comparison results for all strategies using real data: platinum