Abstract
In the last decade, the problem of forecasting time series in very different fields has received increasing attention due to its many real-world applications. In particular, in the very challenging case of financial time series, the underlying phenomenon of stock time series exhibits complex behaviors, including non-stationary, non-linearity and non-trivial scaling properties. In the literature, a wide-used strategy to improve the forecasting capability is the combination of several models. However, the majority of the published researches in the field of financial time series use different machine learning models where only one type of predictor, either linear or nonlinear, is considered. In this paper we first measure relevant features present in the underlying process to propose a forecast method. We select the Sample Entropy and Hurst Exponent to characterize the behavior of stock time series. The characterization reveals the presence of moderate randomness, long-term memory and scaling properties. Thus, based on the measured properties, this paper proposes a novel one-step-ahead off-line meta-learning model, called μ-XNW, for the prediction of the next value xt+1 of a financial time series \(x_{t}\), t = 1, 2, 3, … , that integrates a naive or linear predictor (LP), for which the predicted value of \(x_{t + 1}\) is just repeating the last value \(x_{t}\), an extreme learning machine (ELM) and a discrete wavelet transform (DWT), both based on the nprevious values of \(x_{t + 1}\). LP, ELM and DWT are the constituent of the proposed model μ-XNW. We evaluate the proposed model using four well-known performance measures and validated the usefulness of the model using six high-frequency stock time series belong to the technology sector. The experimental results validate that including internal estimators that are able to the capture the relevant features measured (randomness, long-term memory and scaling properties) successfully improve the accuracy of the forecasting over methods that do not include them.



Similar content being viewed by others
References
Abadi M, Agarwal A, Barham P, Brevdo E, Chen Z, Citro C, Corrado GS, Davis A, Dean J, Devin M, Ghemawat S, Goodfellow I, Harp A, Irving G, Isard M, Jia Y, Jozefowicz R, Kaiser L, Kudlur M, Levenberg J, Mané D, Monga R, Moore S, Murray D, Olah C, Schuster M, Shlens J, Steiner B, Sutskever I, Talwar K, Tucker P, Vanhoucke V, Vasudevan V, Viégas F, Vinyals O, Warden P, Wattenberg M, Wicke M, Yu Y, Zheng X (2015) TensorFlow: Large-scale machine learning on heterogeneous systems. https://www.tensorflow.org/. Software available from tensorflow.org
Adhikari R (2015) A neural network based linear ensemble framework for time series forecasting. Neurocomputing 157:231–242. https://doi.org/10.1016/j.neucom.2015.01.012
Adhikari R, Agrawal RK (2014) A combination of artificial neural network and random walk models for financial time series forecasting. Neural Comput Applic 24(6):1441–1449. https://doi.org/10.1007/s00521-013-1386-y
Aldridge I (2013) High-Frequency Trading: a practical guide to algorithmic strategies and trading systems. Wiley, Hoboken, NJ
Arthur D, Vassilvitskii S (2007) k-means++: the advantages of careful seeding. In: SODA ’07: Proceedings of the eighteenth annual ACM-SIAM symposium on Discrete algorithms, pp 1027–1035. Society for Industrial and Applied Mathematics, Philadelphia
Atsalakis GS, Valavanis KP (2009) Surveying stock market forecasting techniques - part ii: Soft computing methods. Expert Syst Appl 36(3):5932–5941
Bahrammirzaee A (2010) A comparative survey of artificial intelligence applications in finance: Artificial neural networks, expert system and hybrid intelligent systems. Neural Comput Appl 19(8):1165–1195
Bishop CM (1996) Neural networks for pattern recognition. Oxford University Press, USA
Blatter C (2013) Wavelets: Eine einführung (Advanced Lectures in Mathematics) (German Edition) Vieweg+Teubner Verlag
Bollerslev T (1986) Generalized autoregressive conditional heteroskedasticity. J Econ 31(3):307–327
Box GEP, Jenkins G (1970) Time series analysis, forecasting and control. Holden-Day, Incorporated
Box GEP, Jenkins G (1970) Time series analysis, forecasting and control. Holden-Day, Incorporated
Broomhead D, Lowe D (1988) Multivariable functional interpolation and adaptive networks. Complex Systems 2:321–355
Cavalcante RC, Brasileiro RC, Souza VL, Nobrega JP, Oliveira AL (2016) Computational intelligence and financial markets: a survey and future directions. Expert Syst Appl 55:194–211. https://doi.org/10.1016/j.eswa.2016.02.006
Chollet F et al (2015). https://github.com/fchollet/keras
Cybenko G (1989) Approximation by superpositions of a sigmoidal function. Mathematics of Control Signals, and Systems 2:303–314
Dacorogna MM, Gencay R, Muller U, Olsen RB, Olsen OV (2001) An introduction to high frequency finance. Academic Press, New York
Daubechies I (1992) Ten lectures on wavelets. Society for industrial and applied mathematics, Philadelphia
Doucoure B, Agbossou K, Cardenas A (2016) Time series prediction using artificial wavelet neural network and multi-resolution analysis: Application to wind speed data. Renew Energy 92:202–211. https://doi.org/10.1016/j.renene.2016.02.003
Durbin M (2010) All About High-Frequency Trading (All About Series). McGraw-Hill, New York
Elman JL (1990) Finding structure in time. Cogn Sci 14(2):179–211
Engle RF (1982) Autoregressive conditional heteroscedasticity with estimates of the variance of United Kingdom inflation. Econometrica 50(4):987–1007
Fan J, Yao Q (2005) Nonlinear time series: Nonparametric and parametric methods (springer series in statistics). Springer
Gooijer JGD (2017) Elements of nonlinear time series analysis and forecasting (springer series in statistics). Springer
Gooijer JGD, Hyndman RJ (2006) 25 years of time series forecasting. Int J Forecast 22(3):443–473. https://doi.org/10.1016/j.ijforecast.2006.01.001
Granger C, Andersen A (1978) An introduction to bilinear time series models gottingen
Guillaume DM, Dacorogna MM, Davé RR, Muller UA, Olsen RB, Pictet OV (1997) From the bird’s eye to the microscope: A survey of new stylized facts of the intra-daily foreign exchange markets. Finance Stochast 1:95–129
Hamilton JD (1989) A New Approach to the Economic Analysis of Nonstationary Time Series and the Business Cycle. Econometrica 57(2):357–384
Hochreiter S, Schmidhuber J (1997) Long short-term memory. Neural Comput 9(8):1735–1780
Hornik K (1991) Approximation capabilities of multilayer feedforward networks. Neural Netw 4(2):251–257
Hornik K, Stinchcombe M, White H (1989) Multilayer feedforward networks are universal approximators. Neural Netw 2(5):359–366
Hornik K, Stinchcombe MB, White H (1990) Universal approximation of an unknown mapping and its derivatives using multilayer feedforward networks. Neural Netw 3(5):551–560
Huang GB, Wang D, Lan Y (2011) Extreme learning machines: a survey. Int J Machine Learning & Cybernetics 2(2):107–122
Huang GB, Zhu QY, Siew CK (2004) Extreme learning machine: a new learning scheme of feedforward neural networks. In: Proceedings of the 2004 IEEE international joint conference on Neural networks, 2004, vol 2, pp 985–990
Hurst H (1956) Methods of using long-term storage in reservoirs. ICE Proceedings 5:519–543
Hyndman RJ, Khandakar Y (2008) Automatic time series forecasting: The forecast package for r. J Stat Softw 27(3):1–22
Hyndman RJ, Koehler AB, Snyder RD, Grose S (2002) A state space framework for automatic forecasting using exponential smoothing methods. Int J Forecast 18(3):439–454. https://doi.org/10.1016/S0169-2070(01)00110-8
In F, Kim S (2006) Multiscale hedge ratio between the australian stock and futures markets: Evidence from wavelet analysis. Journal of Multinational Financial Management 16(4):411–423. https://doi.org/10.1016/j.mulfin.2005.09.002
Javed K, Gouriveau R, Zerhouni N (2014) Sw-elm: A summation wavelet extreme learning machine algorithm with a priori parameter initialization. Neurocomputing 123:299–307. https://doi.org/10.1016/j.neucom.2013.07.021. http://www.sciencedirect.com/science/article/pii/S0925231213007649. Contains Special issue articles: Advances in Pattern Recognition Applications and Methods
Richman JS, Moorman JR (2000) Physiological time-series analysis using approximate entropy and sample entropy. American Physiological Society 278(6):H2039–H2049
Richman JS, Lake DE, Moorman JR (2004) Sample entropy. Methods Enzymol 384:172–184. https://doi.org/10.1016/S0076-6879(04)84011-4. Numerical Computer Methods, Part E
Kantz H, Schreiber T (2004) Nonlinear time series analysis. Cambridge University Press, Cambridge
Karuppiah J, Los CA (2005) Wavelet multiresolution analysis of high-frequency asian fx rates, summer 1997. International Review of Financial Analysis 14(2):211–246
Lahmiri S (2014) Wavelet low- and high-frequency components as features for predicting stock prices with backpropagation neural networks. Journal of King Saud University - Computer and Information Sciences 26 (2):218–227. https://doi.org/10.1016/j.jksuci.2013.12.001
Lai TL, Xing H (2008) Statistical models and methods for financial markets (springer texts in statistics). Springer
Li S, Goel L, Wang P (2016) An ensemble approach for short-term load forecasting by extreme learning machine. Appl Energy 170:22–29. https://doi.org/10.1016/j.apenergy.2016.02.114
Liao S, Feng C (2014) Meta-elm: {ELM} with {ELM} hidden nodes. Neurocomputing 128:81–87
Ma J, Li Y (2017) Gauss-jordan elimination method for computing all types of generalized inverses related to the 1-inverse. J Comput Appl Math 321:26–43. https://doi.org/10.1016/j.cam.2017.02.010
Makridakis S, Spiliotis E, Assimakopoulos V (2018) Statistical and machine learning forecasting methods: Concerns and ways forward. PLOS ONE 13(3):1–26. https://doi.org/10.1371/journal.pone.0194889
Mallat S (1989) A theory for multiresolution signal decomposition: The wavelet representation. IEEE Transactions on Pattern Analysis and Machine Intelligence 11:674–693
Mallat S (1999) A Wavelet Tour of Signal Processing. Academic Press, San Diego
Mandelbrot BB, Wallis JR (1969) Robustness of the rescaled range r/s in the measurement of noncyclic long run statistical dependence. Water Resour Res 5(5):967–988. https://doi.org/10.1029/WR005i005p00967
Mariano RS, kuen Tse Y (2008) Econometric forecasting and High-Frequency data analysis (lecture notes series, institute for mathematical sciences, national university of singapore). World Scientific Publishing Company
Montavon G, Orr G B, Müller KR (eds.) (2012) Neural Networks: Tricks of the Trade - Second Edition, Lecture Notes in Computer Science, vol. 7700 Springer
Müller UA, Dacorogna MM, Olsen RB, Pictet OV, Schwarz M, Morgenegg C (1990) Statistical study of foreign exchange rates, empirical evidence of a price change scaling law, and intraday analysis. J Bank Financ 14 (6):1189–1208
Palit AK, Popovic D (2010) Computational intelligence in time series forecasting: Theory and engineering applications (advances in industrial control). Springer, Berlin
Percival DB, Walden AT (2006) Wavelet methods for time series analysis (cambridge series in statistical and probabilistic mathematics). Cambridge University Press, Cambridge
Pincus SM (1991) Approximate entropy as a measure of system complexity. Proc Natl Acad Sci 88(6):2297–2301. https://doi.org/10.1073/pnas.88.6.2297
Priestley MB (1980) State-Dependent Models: A general approach to non-linear time series analysis. J Time Series Anal 1(1):47–71
Python PWT (2017). https://pywavelets.readthedocs.io/en/latest/
Qiu T, Guo L, Chen G (2008) Scaling and memory effect in volatility return interval of the chinese stock market. Physica A: Statistical Mechanics and its Applications 387(27):6812– 6818
Rao CR, Mitra SK (1972) Generalized inverse of matrices and its applications (probability & mathematical statistics). Wiley, New York
Sauer T (2011) Numerical analysis, 2nd edn. Addison-Wesley Publishing Company, USA
Shin Y, Ghosh J (1991) The pi-sigma network : an efficient higher-order neural network for pattern classification and function approximation. In: Proceedings of the international joint conference on neural networks, pp 13–18
Shrivastava NA, Panigrahi BK (2014) A hybrid wavelet-elm based short term price forecasting for electricity markets. Int J Electr Power Energy Syst 55:41–50
Shumway RH, Stoffer DS (2006) Time Series Analysis and Its Applications With R Examples. Springer, Berlin. ISBN 978-0-387-29317-2
Strang G, Nguyen T (1997) Wavelets and filter banks. Wellesley-Cambridge Press, Cambridge
Sun ZL, Choi TM, Au KF, Yu Y (2008) Sales forecasting using extreme learning machine with applications in fashion retailing. Decis Support Syst 46(1):411–419
Tong H (1983) Threshold models in nonlinear time series analysis. Springer, Berlin
Trefethen LN, Bau D (1997) Numerical linear algebra. SIAM
Tsay RS (2012) An introduction to analysis of financial data with R. wiley, New York
Zhang Q, Benveniste A (1992) Wavelet networks. IEEE Trans Neural Networks 3(6):889–898
Zubulake P, Lee S (2011) The high frequency game changer: How automated trading strategies have revolutionized the markets (wiley trading), Wiley, New York
Acknowledgments
This work has been partially funded by the Centro Científico Tecnológico de Valparaíso – CCTVal, CONICYT PIA/Basal Funding FB0821, FONDECYT 1150810, FONDECYT 11160744 and UTFSM PIIC2015. The authors gratefully thanks Alejandro Cañete from IFITEC S.A. – Financial Technology, for providing the stock time series for this study.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interests
The authors declare that they have no conflicts of interest.
Appendices
Appendix A: Sample entropy
Pincus [58] adapted the notion of ”entropy” for real-world use. In this context, entropy means order or regularity or complexity. Fix \(m,N \in \mathbf {N}\) with \(m\leq N\), and \(r \in \mathbf {R}^{+}\). Given a time series of data \(u(1), u(2),\dots , u(N)\) from measurements equally spaced in time, form the sequence of vectors\(\mathbf {x}(1)\), \(\mathbf {x}(2)\), …, \(\mathbf {x}(N-m + 1) \in \mathbf {R}^{m}\) defined by:
Let d be some norm in \(\mathbf {R}^{m}\), for instance:
Then, Pincus defines
The denominator \(N-m + 1\) in (36) is the total number of segments of length m available in the signal \(u(1),\dots , u(N)\), i.e. \(1\leq \text {numerator}\leq N-m + 1\). Note that in the numerator of (36) the distance from the pattern (segment, template, or vector) \(\mathbf {x}(i)\) must be measured w.r.t. all\(N-m + 1\) patterns of length m available in the sequence \(u(1),\dots , u(N)\). Only the patterns with distance \(\leq r\) are counted. Thus:
We observe that, for \(i\in \mathbf {N}\) fixed with \(i\leq N-m + 1\):
where H is the Heaviside step function. Thus,
Pincus further defines
and
In order to explain in deep the sample entropy measure, we introduce the following notation:
Recall that \({C_{i}^{m}}(r)\) counts those templates \(\mathbf {x}(j)\equiv u[j:j+m-1]\) of the signal \(u[1:N]\), whose \(\|\cdot \|_{\infty }\)-distance to the fixed template \(\mathbf {x}(i)\equiv u[i:i+m-1]\) is \(\leq r\).
Richman and Moorman [40] define:
Note that there are \(N-m + 1\) templates \(\mathbf {x}_{m}(j)\) of length m in the signal \(u[1:N]\). However, the convention of Richman-Moorman is to consider for \({B_{i}^{m}}(r)\) only \(N-m\) of them, for instance, the first \(N-m\) of them, thus disregarding the template \(\mathbf {x}_{m}(N-m + 1)\equiv u[N-m + 1:N]\sqsubset u[1:N]\). In the case of \({A_{i}^{m}}(r)\), there are exactly \(N-m\) templates of length \(m + 1\) in \(u[1:N]\). Then Richman and Moorman define the corresponding integral coefficients:
Thus,
“To match withinr” means here that the distance
We observe that:
Consider now the set in the argument of \(\mathscr{P}\). Let us call it S:
The measure of this set is, of course, \(A^{m}(r)\):
Thus,
Loosely speaking we can say that this is the conditional probability that two different templates of length \(m + 1\), whose m initial points are within a tolerance r of each other, remain within the tolerance r of each other at the next point (the \(m + 1\)-th point of the template).
Richman and Moorman define then the statistic:
and the corresponding parameter estimated by this statistic, as:
Appendix B: Wavelet transform background
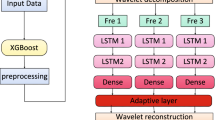
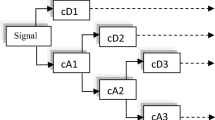
Wavelet analysis is today a common tool in signal and spectral analysis, in particular because of its multiresolution and localization capabilities both in time and frequency domain. In the time series context, wavelet analysis allows the decomposition and localization, at different time and frequency scales, relevant features present on the underlying processes. The literature on wavelet theory is extensive; we mention just a few standard references: [9, 18, 51, 57]. In this section we collect the bare minimum of wavelet theory, necessary for the best understanding of the algorithms developed in the next section.
1.1 B1 Continuous wavelet transform
A function \(\psi :\mathbb {R}\to \mathbb {C}\), such that \(\psi \in L^{2}\) and \(\|\psi \|^{2} = {\int }_{-\infty }^{\infty }|\psi (x)|^{2} dt = 1\), is called wavelet or mother-wavelet whenever \(\psi \) satisfies the admissibility condition:
where \(\widehat {\psi }\) denotes the Fourier transform of \(\psi \). Note that (48) implies that \(\psi \) must have zero average, i.e., \(\widehat {\psi }(0)=\frac {1}{\sqrt {2\pi }} {\int }_{-\infty }^{\infty } \psi (t) dt= 0\). When a fixed wavelet \(\psi \in L^{2}\) has been selected, then the continuous wavelet-transform of a time signal \(f\in L^{2}\) is defined by:
where \(\overline {\psi ((t-b)/a)}\) denotes the complex conjugate of \(\psi ((t-b)/a)\). Then f can be synthesized from its wavelet transform \(\mathcal {W}\!f\) by means of the inversion formula: [9, (3.7), p. 67], [51, Th. 4.3, p. 81].
1.2 B2 Discrete wavelet transform
A well known approach to discrete wavelet analysis is by means of multiresolution analysis (MRA). Main references for this section are [9, Ch. 5, p. 105], [51, Ch. VII, p. 220]. MRA provides a systematic way to construct discrete wavelets. An MRA is a sequence \(\left \{V_{j}\right \}_{j\in \mathbb {Z}}\) of closed subspaces of \(L^{2}\) having the following properties also known as axioms: [9, Sec. 5.1, p. 106], [51, Def. 7.1, p. 220],
-
(a)
Vj ⊂ Vj− 1 for all \(j\in \mathbb {Z}\);
-
(b)
\(\bigcap _{j\in \mathbb {Z}}V_{j}=\{0\}\) (axiom of separation);
-
(c)
\(\bigcup _{j\in \mathbb {Z}}V_{j}\) is dense in \(L^{2}\) (axiom of completeness);
-
(d)
f ∈ Vj ⇔ f(∙− 2jk) ∈ Vj;
-
(e)
f ∈ Vj ⇔ f(∙/2) ∈ Vj+ 1 (or, equivalently, \(f(2\cdot \bullet )\in V_{j} \Leftrightarrow f\in V_{j + 1}\), obviously); and
-
(f)
(Blatter) There exists a function \(\phi \in L^{2}\cap L^{1}\) such that \(\left \{ \phi (\bullet -k) \right \}_{k\in \mathbb {Z}}\) is an orthonormal basis of \(V_{0}\). This function \(\phi \) is called scaling function of the MRA.
For each \(j\in \mathbb {Z}\) the functions,
constitute an orthonormal basis of \(V_{j}\).
Since \(\phi \in V_{0}\subset V_{-1}\), \(\phi \) can be represented in terms of the orthonormal basis (51) of \(V_{-1}\) (i.e., \(j=-1\)). In fact, the inclusion \(V_{0}\subset V_{-1}\) is equivalent to the existence of a sequence \(\{h_{k}\}_{k\in \mathbb {Z}}\) with \({\sum }_{k\in \mathbb {Z}}|h_{k}|^{2}\leq \infty \) such that the scaling equation (52) holds: [9, p. 118, eq. (2)]
The sequence \(\{h_{k}\}_{k\in \mathbb {Z}}\) uniquely defines the scaling function \(\phi \). Axiom (a) is an obstruction for the functions \(\phi _{j,k}\) to build an orthonormal basis of \(L^{2}\). One considers then an additional system of pairwise orthogonal subspaces \(W_{j}\) of \(L^{2}\), defined as the orthogonal complements of \(V_{j}\) in \(V_{j-1}\), so that \(V_{j-1}=V_{j}\oplus W_{j}\), \(V_{j}\perp W_{j}\), \(j\in \mathbb {Z}\), having the property:
which is analogous to axiom (e). The orthogonal direct sum of these subspaces: [9, p. 108, (5.1)],
There is moreover a function \(\psi \in W_{0}\), called the mother wavelet, such that \(\{\psi (\bullet -k)\}_{k\in \mathbb {Z}}\) is an orthonormal basis of \(W_{0}\), given by: [9, pp. 123-4, eqs. (16)–(19)]
where \(\overline {h_{-k-1}}\) denotes the complex conjugate of \(h_{-k-1}\). Moreover, the function system \(\{\psi _{j,k}\}_{j,k\in \mathbb {Z}}\) defined by: [9, p. 124, (5.13)]
is an orthonormal wavelet-basis of \(L^{2}(\mathbb {R})\).
1.3 B.3 Algorithms
We start from (52) and (55). From (52) follows for \(j,n\in \mathbb {Z}\) the identity:
which is usually written as a recursive formula “ϕj− 1,∙” \(\to \) “ϕj,∙” as: [9, p. 131, eq. (3)]
Similarly, the recursive formula “ϕj− 1,∙” \(\to \) “ψj,∙” is given by: [9, p. 131, eq. (4)]
The well-known fast filter bank algorithm allows the computation of the orthogonal wavelet coefficients of a signal \(f\in L^{2}\). Since at the scale j, \(\{\phi _{j,n}\}_{n\in \mathbb {Z}}\) and \(\{\psi _{j,n}\}_{n\in \mathbb {Z}}\) are orthonormal bases of \(V_{j}\) and \(W_{j}\) respectively, the projections of f ontho these spaces are given by: [51, p. 255]
These coefficients can be calculated recursively with a cascade of discrete convolutions and subsamplings. [51, p. 255, Theorem 7.7] At the analysis or decomposition:
and at the synthesis or reconstruction:
Appendix C: Parameter setting of forecasting models
Tables 10 and 11 show the best setting obtained by the training process in each neural network model. The activation functions correspond to Hyperbolic Tangent (Tanh), Logistic (Log), Softsign (Ssgn) and SoftPlus (Spls) and Identity (Id). The best fitting in RFB in the hidden layer, these were: Cubic (Cub) and Multiquadric (MQ). In MLP, PSN, LSTM, the setting corresponds to number of inputs, number of hidden neurons, activation function in hidden layer and activation function in output layer. ELME1 and ENN follow the same notation previous, however, only consider an activation function on the hidden layer. In the case of SW-ELM, the notation only considers the number of inputs and hidden nodes, since the model uses a particular activation function. In the case of ARIMA model, the best settings are shown in Table 12
Appendix D: Computational Complexity
The forecasting models exhibited in this study were implemented in Python and R, and the execution times were measured in seconds using the modules time (Python) and tictoc (R). To ensure a sequential execution inside each individual model, or inside each individual model constituent, the number of execution threads was set to 1. More precisely, the number of threads of the OPENBLAS environmental variable was set to 1: OPENBLAS_NUM_THREADS= 1.
In Section 5.5.1 we calculate the number of elementary operations (\(\mathscr{T}_{\text {WE}}\)) required to find the best WE architecture. Table 13 shows the mother wavelets used for fitting the WE models and theirs corresponding indices.
Tables 14 and 15 show the CC-values for each forecasting model and time series. The execution time for the naive model is 0.0000024594 seconds in mean for each time series.
Tables 16 and 17 show the CC-values and THEIL-values for ELMEk models for each time series.
The execution environment used to obtain the experimental results is shown in Table 18.
Rights and permissions
About this article
Cite this article
Fernández, C., Salinas, L. & Torres, C.E. A meta extreme learning machine method for forecasting financial time series. Appl Intell 49, 532–554 (2019). https://doi.org/10.1007/s10489-018-1282-3
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10489-018-1282-3