Skip to main content
SpringerLink
Log in

An intuitionistic linguistic MCDM model based on probabilistic exceedance method and evidence theory

  • Published:
Applied Intelligence Aims and scope Submit manuscript

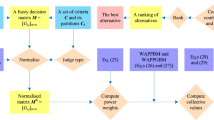
Abstract

The optimization in multi-criteria decision making under uncertain conditions has attracted more and more scholars in recent years. However, it is still an open issue that how to better evaluate the satisfaction with more complex objects. Since the great performance of intuitionistic fuzzy set on handling the uncertain information, in this paper, a new fuzzy linguistic model for non-scalar criteria satisfaction expressed via intuitionistic fuzzy sets is proposed, which makes experts evaluate more objectively. Moreover, a corresponding aggregation approach based on the Choquet probabilistic exceedance method is also proposed. After a series of calculation processes, the final aggregated results embodied by intuitionistic fuzzy sets (IFSs) can be obtained. Then by converting them into the belief intervals, the best alternative can be selected more objectively. In addition, two real-life applications are shown to demonstrate the practicality of proposed method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

References

  1. Liu Z, Xiao F, Lin C, Kang BH, Cao Z (2019) A generalized golden rule representative value for multiple-criteria decision analysis. IEEE Trans Syst Man Cybern: Syst, 1–12. https://doi.org/10.1109/TSMC.2019.2919243

  2. Zavadskas EK, Antucheviciene J, Chatterjee P (2019) Multiple-criteria decision-making (MCDM) techniques for business processes information management. Information 10(1):4

    Google Scholar 

  3. Xiao F, Ding W (2019) Divergence measure of Pythagorean fuzzy sets and its application in medical diagnosis. Appl Soft Comput 79:254–267

    Google Scholar 

  4. Mardani A, Jusoh A, Zavadskas EK (2015) Fuzzy multiple criteria decision-making techniques and applications - two decades review from 1994 to 2014. Expert Syst Appl 42(8):4126–4148

    Google Scholar 

  5. Yager RR (2018) On using the shapley value to approximate the choquet integral in cases of uncertain arguments. IEEE Trans Fuzzy Syst 26(3):1303–1310

    Google Scholar 

  6. Tan C, Chen X (2010) Intuitionistic fuzzy Choquet integral operator for multi-criteria decision making. Expert Syst Appl 37(1):149–157

    Google Scholar 

  7. Xu Z (2010) Choquet integrals of weighted intuitionistic fuzzy information. Inform Sci 180(5):726–736

    MathSciNet  MATH  Google Scholar 

  8. Wu X, Liao H (2018) An approach to quality function deployment based on probabilistic linguistic term sets and ORESTE method for multi-expert multi-criteria decision making. Inform Fus 43:13–26

    Google Scholar 

  9. Feng F, Cho J, Pedrycz W, Fujita H, Herawan T (2016) Soft set based association rule mining. Knowl-Based Syst 111:268–282

    Google Scholar 

  10. Yager RR (2015) On the owa aggregation with probabilistic inputs. Int J Uncertain Fuzziness Knowl-Based Syst 23(Suppl 1):143–162

    MathSciNet  MATH  Google Scholar 

  11. Yager RR (2018) A class of belief structures based on possibility measures. Soft Comput 22(23):7909–7917

    MATH  Google Scholar 

  12. Yager RR (2016) Evaluating choquet integrals whose arguments are probability distributions. IEEE Trans Fuzzy Syst 24(4):957–965

    Google Scholar 

  13. Grabisch M (1995) Fuzzy integral in multicriteria decision making. Fuzzy Sets Syst 69(3):279–298

    MathSciNet  MATH  Google Scholar 

  14. Yager RR, Alajlan N (2018) Multi-criteria formulations with uncertain satisfactions. Eng Appl AI 69:104–111

    Google Scholar 

  15. Mardani A, Nilashi M, Zavadskas EK, Awang S, Zare H, Jamal NM (2018) Decision making methods based on fuzzy aggregation operators: three decades review from 1986 to 2017. Int J Inf Technol Decis Mak 17(2):391–466

    Google Scholar 

  16. Wang X, Xu Z, Gou X (2019) Nested probabilistic-numerical linguistic term sets in two-stage multi-attribute group decision making. Appl Intell 49(7):2582–2602. https://doi.org/10.1007/s10489-018-1392-y

    Google Scholar 

  17. Herrera F, Herrera-Viedma E, Martinez L (2000) A fusion approach for managing multi-granularity linguistic term sets in decision making. Fuzzy Set Syst 114(1):43–58

    MATH  Google Scholar 

  18. Gou X, Xu Z, Liao H (2017) Multiple criteria decision making based on bonferroni means with hesitant fuzzy linguistic information. Soft Comput 21(21):6515–6529

    MATH  Google Scholar 

  19. Atanassov KT (1986) Intuitionistic fuzzy sets. Fuzzy Sets Syst 20(1):87–96

    MATH  Google Scholar 

  20. Gupta P, Lin C, Mehlawat MK, Grover N (2016) A new method for intuitionistic fuzzy multiattribute decision making. IEEE Trans Syst Man Cybern: Syst 46(9):1167–1179

    Google Scholar 

  21. Bustince H, Burillo P (1996) Vague sets are intuitionistic fuzzy sets. Fuzzy Sets Syst 79(3):403–405

    MathSciNet  MATH  Google Scholar 

  22. Atanassov KT (1999) Interval valued intuitionistic fuzzy sets. In: Intuitionistic fuzzy sets. Springer, pp 139–177

  23. Miguel LD, Bustince H, Pekala B, Bentkowska U, da Silva IA, Bedregal BRC, Mesiar R, Ochoa G (2016) Interval-valued atanassov intuitionistic OWA aggregations using admissible linear orders and their application to decision making. IEEE Trans Fuzzy Syst 24(6):1586–1597

    Google Scholar 

  24. Reiser RHS, Bedregal BRC (2017) Correlation in interval-valued atanassov’s intuitionistic fuzzy sets - conjugate and negation operators. Int J Uncertain Fuzziness Knowl-Based Syst 25(5):787–820

    MathSciNet  MATH  Google Scholar 

  25. Torra V (2010) Hesitant fuzzy sets. Int J Intell Syst 25(6):529–539

    MATH  Google Scholar 

  26. Montserrat-Adell J, Xu Z, Gou X, Agell N (2019) Free double hierarchy hesitant fuzzy linguistic term sets: an application on ranking alternatives in GDM. Inform Fus 47:45–59

    Google Scholar 

  27. Xia M, Chen J, Zeng X-J (2018) Decision analysis on choquet integral-based multi-criteria decision-making with imprecise information. Int J Inform Technol Decis Making 17(02):677–704

    Google Scholar 

  28. Zhou L, Zhou Y, Liu X, Chen H (2015) Some ILOWA operators and their applications to group decision making with additive linguistic preference relations. J Intell Fuzzy Syst 29(2):831–843

    MathSciNet  MATH  Google Scholar 

  29. Liu P (2013) Some geometric aggregation operators based on interval intuitionistic uncertain linguistic variables and their application to group decision making. Appl Math Model 37(4):2430–2444

    MathSciNet  MATH  Google Scholar 

  30. Beliakov G, Bustince H, Goswami D, Mukherjee U, Pal NR (2011) On averaging operators for atanassov’s intuitionistic fuzzy sets. Inform Sci 181(6):1116–1124

    MathSciNet  MATH  Google Scholar 

  31. Kang B, Deng Y (2019) The maximum Deng entropy. IEEE Access 7(1):120758–120765

    Google Scholar 

  32. Liu Z, Xiao F (2019) An evidential aggregation method of intuitionistic fuzzy sets based on belief entropy. IEEE Access 7:68905–68916

    Google Scholar 

  33. Luo Z, Deng Y (2019) A matrix method of basic belief assignment’s negation in Dempster-Shafer theory. IEEE Trans Fuzzy Syst 27, https://doi.org/10.1109/TFUZZ.2019.2930027

  34. Zadeh LA (1986) A simple view of the dempster-shafer theory of evidence and its implication for the rule of combination. AI Mag 7(2):85–85

    Google Scholar 

  35. Zhou M, Liu X-B, Chen Y-W, Yang J-B (2018) Evidential reasoning rule for MADM with both weights and reliabilities in group decision making. Knowl-Based Syst 143:142–161

    Google Scholar 

  36. Seiti H, Hafezalkotob A, Najafi SE, Khalaj M (2019) Developing a novel risk-based mcdm approach based on d numbers and fuzzy information axiom and its applications in preventive maintenance planning. Appl Soft Comput 82:105559

    Google Scholar 

  37. Zhao J, Deng Y (2019) Performer selection in human reliability analysis: D numbers approach. Int J Comput Commun Control 14(4):521–536

    MathSciNet  Google Scholar 

  38. Zadeh LA (2011) A note on z-numbers. Inform Sci 181(14):2923–2932

    MathSciNet  MATH  Google Scholar 

  39. Massanet S, Riera JV, Torrens J (2020) A new approach to zadeh’s Z-numbers: mixed-discrete z-numbers. Inform Fus 53:35–42

    Google Scholar 

  40. Liu Z, Pan Q, Dezert J, Han J-W, He Y (2018) Classifier fusion with contextual reliability evaluation. IEEE Trans Cybern 48(5):1605–1618

    Google Scholar 

  41. Sentz K, Ferson S, et al. (2002) Combination of evidence in Dempster-Shafer theory, vol 4015. Citeseer

  42. Zhang W, Deng Y (2019) Combining conflicting evidence using the DEMATEL method. Soft Comput 23:8207–8216

    Google Scholar 

  43. Fu C, Xue M, Xu D-L, Yang S-L (2019) Selecting strategic partner for tax information systems based on weight learning with belief structures. Int J Approx Reason 105:66–84

    MathSciNet  MATH  Google Scholar 

  44. Wang X, Song Y (2018) Uncertainty measure in evidence theory with its applications. Appl Intell 48 (7):1672–1688

    Google Scholar 

  45. Song Y, Deng Y (2019) Divergence measure of belief function and its application in data fusion. IEEE Access 7(1):107465–107472

    Google Scholar 

  46. Liu Y, Pal NR, Marathe AR, Lin C (2018) Weighted fuzzy dempster-shafer framework for multimodal information integration. IEEE Trans Fuzzy Syst 26(1):338–352

    Google Scholar 

  47. Li Y, Deng Y (2018) Generalized ordered propositions fusion based on belief entropy. Int J Comput Commun Control 13(5):792–807

    Google Scholar 

  48. Dempster A (1967) Upper and lower probabilities induced by a multivalued mapping. Ann Math Stat 38 (2):325–339

    MathSciNet  MATH  Google Scholar 

  49. Shafer G (1976) A mathematical theory of evidence. Princeton University Press, Princeton

    MATH  Google Scholar 

  50. Dempster A (1967) Upper and lower probabilities induced by a multivalued mapping. Ann Math Stat, 325–339

  51. Song Y, Wang X (2017) A new similarity measure between intuitionistic fuzzy sets and the positive definiteness of the similarity matrix. Pattern Anal Appl 20(1):215–226

    MathSciNet  MATH  Google Scholar 

  52. Garg H, Arora R (2018) Generalized and group-based generalized intuitionistic fuzzy soft sets with applications in decision-making. Appl Intell 48(2):343–356

    Google Scholar 

  53. Feng F, Liang M, Fujita H, Yager RR, Liu X (2019) Lexicographic orders of intuitionistic fuzzy values and their relationships. Mathematics 7(2):1–26

    Google Scholar 

  54. Das S, Guha D, Dutta B (2016) Medical diagnosis with the aid of using fuzzy logic and intuitionistic fuzzy logic. Appl Intell 45(3):850–867. https://doi.org/10.1007/s10489-016-0792-0

    Article  Google Scholar 

  55. Li Y, Deng Y (2019) Intuitionistic evidence sets. IEEE Access 7(1):106417–106426

    Google Scholar 

  56. Song Y, Wang X, Zhu J, Lei L (2018) Sensor dynamic reliability evaluation based on evidence theory and intuitionistic fuzzy sets. Appl Intell 48(11):3950–3962. https://doi.org/10.1007/s10489-018-1188-0

    Google Scholar 

  57. Xiao F (2019) EFMCDM: evidential fuzzy multicriteria decision making based on belief entropy. IEEE Transactions on Fuzzy Systems. https://doi.org/10.1109/TFUZZ.2019.2936368

  58. Dymova L, Sevastjanov P (2010) An interpretation of intuitionistic fuzzy sets in terms of evidence theory: decision making aspect. Knowl-Based Syst 23(8):772–782

    Google Scholar 

  59. Dymova SPL (2010) Risk assessment of construction projects. The operations on interval-valued intuitionistic fuzzy values in the framework of Dempster–Shafer theory 16(1):33–46

    Google Scholar 

  60. Yang C, Zou Y, Lai P, Jiang N (2015) Data mining-based methods for fault isolation with validated FMEA model ranking. Appl Intell 43(4):913–923. https://doi.org/10.1007/s10489-015-0674-x

    Article  Google Scholar 

  61. Liu Z, Xiao F (2019) An intuitionistic evidential method for weight determination in FMEA based on belief entropy. Entropy 21(2):211

    MathSciNet  Google Scholar 

  62. Song Y, Wang X, Wu W, Lei L, Quan W (2017) Uncertainty measure for atanassov’s intuitionistic fuzzy sets. Appl Intell 46(4):757–774

    Google Scholar 

  63. Szmidt E, Kacprzyk J (2002) Using intuitionistic fuzzy sets in group decision making. Control Cybern 31:1055–1057

    MATH  Google Scholar 

Download references

Acknowledgments

This research is supported by the Fundamental Research Funds for the Central Universities (No. XDJK2019C085) and Chongqing Overseas Scholars Innovation Program (No. cx2018077).

Author information

Authors and Affiliations

  1. School of Computer and Information Science, Southwest University, Chongqing, 400715, China

    Zeyi Liu & Fuyuan Xiao

Authors
  1. Zeyi Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Fuyuan Xiao
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Fuyuan Xiao.

Additional information

Publisher’s note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Liu, Z., Xiao, F. An intuitionistic linguistic MCDM model based on probabilistic exceedance method and evidence theory. Appl Intell 50, 1979–1995 (2020). https://doi.org/10.1007/s10489-020-01638-y

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10489-020-01638-y

Keywords

Search

Navigation