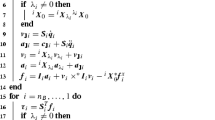Abstract
This paper presents new recursive dynamics algorithms that enable operational-space control of floating-base systems to be performed at faster rates. This type of control approach requires the computation of operational-space quantities and suffers from high computational order when these quantities are directly computed through the use of the mass matrix and Jacobian from the joint-space formulation. While many efforts have focused on efficient computation of the operational-space inertia matrix \({\varvec{{\Lambda }}}\), this paper provides a recursive algorithm to compute all quantities required for floating-base control of a tree-structure mechanism. This includes the first recursive algorithm to compute the dynamically consistent pseudoinverse of the Jacobian \({\,\, \bar{{\varvec{\!\!J}}}}\) for a tree-structure system. This algorithm is extended to handle arbitrary contact constraints with the ground, which are often found in legged systems, and uses effective ground contact dynamics approximations to retain computational efficiency. The usefulness of the algorithm is demonstrated through application to control of a high-speed quadruped trot in simulation. Our contact-consistent algorithm demonstrates pitch and roll stabilization for a large dog-sized quadruped running at 3.6 m/s without any contact force sensing, and is shown to outperform a simpler Raibert-style posture controller. In addition, the operational-space control approach allows the dynamic effects of the swing legs to be effectively accounted for at this high speed.












Similar content being viewed by others
Notes
Upright characters \(\mathbf{v}\) and \(\mathbf{f}\) will be used to represent a spatial velocity and force, respectively. Script characters \({\varvec{v}}\) and \({\varvec{f}}\) will be used to denote the linear velocity or force component of a spatial quantity (Featherstone and Orin 2008).
Defining \(fl(x~op~y)\) as the floating-point value returned by a standard arithmetic operation (addition, multiplication, etc.), IEEE standard arithmetic satisfies \(fl(x~op~y) = (x~op~y) ( 1+ \delta )\) where \(|\delta |\le \epsilon _{mach}/2\) represents a normalized rounding error (Higham 2002). \(\epsilon _{mach}\) is the machine epsilon which provides an upper bound on the maximum normalized distance from any floating-point number to a neighboring floating-point number.
Cases which require active modification of the GRFs to comply with frictional limits would be able to fall back on more complex task-space control approaches by Wensing and Orin (2013).
References
Ahmadi, M., & Buehler, M. (1997). Stable control of a simulated one-legged running robot with hip and leg compliance. IEEE Transactions on Robotics and Automation, 13(1), 96–104.
Bhalerao, K., Critchley, J. H., Oetomo, D., Featherstone, R., & Khatib, O. (2013). Distributed operational space formulation. ASME Journal of Computational and Nonlinear Dynamics, 9(2), 1–10. doi:10.1115/1.4025577
Chang, K.-S., & Khatib, O. (2001). Efficient recursive algorithm for the operational space inertia matrix of branching mechanisms. Advanced Robotics, 14(8), 703–715.
de Sapio, V., & Khatib, O. (2005). Operational space control of multibody systems with explicit holonomic constraints. In IEEE international conference on robotics and automation (pp. 2950–2956).
Eigen, (2014). http://eigen.tuxfamily.org.
Featherstone, R. (1983). The calculation of robot dynamics using articulated-body inertias. The International Journal of Robotics Research, 2(1), 13–30.
Featherstone, R. (1999a). A divide-and-conquer articulated-body algorithm for parallel O(log(n)) calculation of rigid-body dynamics. Part 1: Basic algorithm. The International Journal of Robotics Research, 18(9), 867–875.
Featherstone, R. (1999b). A divide-and-conquer articulated-body algorithm for parallel O(log(n)) calculation of rigid-body dynamics. Part 2: Trees, loops, and accuracy. The International Journal of Robotics Research, 18(9), 876–892.
Featherstone, R. (2001). The acceleration vector of a rigid body. The International Journal of Robotics Research, 20(11), 841–846.
Featherstone, R. (2008). Rigid body dynamics algorithms. Berlin: Springer.
Featherstone, R. (2010a). A beginner’s guide to 6-D vectors (Part 1). IEEE Robotics Automation Magazine, 17(3), 83–94.
Featherstone, R. (2010b). A beginner’s guide to 6-D vectors (Part 2). IEEE Robotics Automation Magazine, 17(4), 88–99.
Featherstone, R., & Orin, D. (2008). Chapter 2: Dynamics. In B. Siciliano & O. Khatib (Eds.), Springer handbook of robotics. New York: Springer.
Heglund, N. C., & Taylor, C. R. (1988). Speed, stride frequency and energy cost per stride: How do they change with body size and gait? Journal of Experimental Biology, 138(1), 301–318.
Higham, N. J. (2002). Accuracy and stability of numerical algorithms (2nd ed.). Philadelphia, PA: Society for Industrial and Applied Mathematics.
Hutter, M., Hoepflinger, M., Gehring, C., Bloesch, M., Remy, C. D., & Siegwart, R. (2012). Hybrid operational space control for compliant legged systems. In N. Roy, P. Newman, & S. Srinivasa (Eds.), Robotics: Science and systems VIII (pp. 129–136). Cambridge: MIT Press.
Hyon, S.-H., & Mita, T. (2002). Development of a biologically inspired hopping robot. In Proceedings of the IEEE international conference on robotics and automation (Vol. 4, pp. 3984–3991).
Jain, A. (2013). Operational space inertia for robots with internal loops. In Proceedings of multibody dynamics (pp. 297–304). Zagreb, Croatia.
Khatib, O. (1987). A unified approach for motion and force control of robot manipulators: The operational space formulation. IEEE Journal of Robotics and Automation, 3(1), 43–53.
Kreutz-Delgado, K., Jain, A., & Rodriguez, G. (1991). Recursive formulation of operational space control. In Proceedings of the IEEE international conference on robotics and automation (pp. 1750–1753).
Lathrop, R. (1986). Constrained (closed-loop) robot simulation by local constraint propagation. In Profeedings of the IEEE international conference on robotics and automation (Vol. 3, pp. 689–694).
Lilly, K., & Orin, D. (1993). Efficient O(N) recursive computation of the operational space inertia matrix. IEEE Transactions on Systems, Man and Cybernetics, 23(5), 1384–1391.
Lilly, K. W. (1989). Efficient dynamic simulation of robotic mechanisms. PhD thesis, The Ohio State University.
Lilly, K. W. (1993). Efficient dynamic simulation of robotic mechanisms. Norwell, MA, USA: Kluwer Academic Publishers.
Luh, J. Y. S., Walker, M. W., & Paul, R. P. C. (1980). On-line computational scheme for mechanical manipulators. ASME Journal of Dynamic Systems, Measurement, and Control, 102(2), 69–76.
Marhefka, D. W., Orin, D. E., Schmiedeler, J. P., & Waldron, K. J. (2003). Intelligent control of quadruped gallops. IEEE/ASME Transactions on Mechatronics, 8(4), 446–456.
McMahon, T. (1985). The role of compliance in mammalian running gaits. Journal of Experimental Biology, 115(1), 263–282.
McMillan, S., Sadayappan, P., & Orin, D. (1994). Efficient dynamic simulation of multiple manipulator systems with singular configurations. IEEE Transactions on Systems, Man and Cybernetics, 24(2), 306–313.
Mistry, M., & Righetti, L. (2011). Operational space control of constrained and underactuated systems. In H. Durrant-Whyte, N. Roy, & P. Abbeel (Eds.), Robotics: Science and Systems VII (pp. 225–232). Cambridge: MIT Press.
Nichol, J. G., Singh, S. P., Waldron, K. J., Palmer, L. R., & Orin, D. E. (2004). System design of a quadrupedal galloping machine. The International Journal of Robotics Research, 23(10–11), 1013–1027.
Orin, D. E., Goswami, A., & Lee, S.-H. (2013). Centroidal dynamics of a humanoid robot. Autonomous Robots, 35(2), 161–176.
Palmer, L., & Orin, D. (2007). Force redistribution in a quadruped running trot. In IEEE International conference on robotics and automation (pp. 4343–4348).
Palmer, L., & Orin, D. (2010). Intelligent control of high-speed turning in a quadruped. Journal of Intelligent & Robotic Systems, 58, 47–68.
Palmer, L. R., Orin, D. E., Marhefka, D. W., Schmiedeler, J. P., & Waldron, K. J. (2003). Intelligent control of an experimental articulated leg for a galloping machine. In Proceeding of the IEEE international conference on robotics and automation (Vol. 3, pp. 3821–3827).
Park, J., & Khatib, O. (2006). Contact consistent control framework for humanoid robots. In Proceedings of the IEEE international conference on robotics and automation (pp. 1963–1969).
Raibert, M., Blankespoor, K., Nelson, G., Playter, R., et al. (2008). Bigdog, the rough-terrain quadruped robot. In Proceedings of the 17th IFAC World Congress (pp. 10823–10825).
Raibert, M. H. (1986). Legged robots that balance. Cambridge, MA, USA: MIT Press.
Raibert, M. H. (1990). Trotting, pacing and bounding by a quadruped robot. Journal of Biomechanics, 23, 79–98.
Roberson, R. E., & Schwertassek, R. (1988). Dynamics of multibody systems. Berlin/Heidelberg/New York: Springer.
Rodenbaugh, S. (2003). RobotBuilder: A graphical software tool for the rapid development of robotic dynamic simulations. Master’s thesis, The Ohio State University, Columbus.
Rodriguez, G., Jain, A., & Kreutz-Delgado, K. (1992). Spatial operator algebra for multibody system dynamics. Journal of the Astronautical Sciences, 40, 27–50.
Russakow, J., Khatib, O., & Rock, S. (1995). Extended operational space formulation for serial-to-parallel chain (branching) manipulators. In Proceedings of the IEEE international conference on robotics and automation (pp. 1056–1061).
Schmiedeler, J. P., & Waldron, K. J. (1999). The mechanics of quadrupedal galloping and the future of legged vehicles. The International Journal of Robotics Research, 18(12), 1224–1234.
Schmiedeler, J. P., & Waldron, K. J. (2002). Leg stiffness and articulated leg design for dynamic locomotion. In Proceedings of the ASME international design engineering technical conferences (Vol. 5, pp. 1105–1112).
Sentis, L., & Khatib, O. (2005). Control of free-floating humanoid robots through task prioritization. In Proceedings of the IEEE international conference on robotics and automation (pp. 1718–1723).
Sentis, L., Park, J., & Khatib, O. (2010). Compliant control of multicontact and center-of-mass behaviors in humanoid robots. IEEE Transaction on Robotics, 26(3), 483–501.
Sentis, L., Petersen, J., & Philippsen, R. (2013). Implementation and stability analysis of prioritized whole-body compliant controllers on a wheeled humanoid robot in uneven terrains. Autonomous Robots, 35(4), 301–319.
Waldron, K., & Schmiedeler, J. (2008). Chapter 1: Kinematics. In B. Siciliano & O. Khatib (Eds.), Springer handbook of robotics. New York: Springer.
Walker, M. W., & Orin, D. E. (1982). Efficient dynamic computer simulation of robotic mechanisms. ASME Journal of Dynamic Systems, Measurement, and Control, 104(3), 205–211.
Wensing, P., Featherstone, R., & Orin, D. E. (2012). A reduced-order recursive algorithm for the computation of the operational-space inertia matrix. In IEEE international conference on robotics and automation (pp. 4911–4917).
Wensing, P. M., & Orin, D. E. (2013). Generation of dynamic humanoid behaviors through task-space control with conic optimization. In IEEE international conference on robotics and automation (pp. 3088–3094).
Wensing, P. M., Hammam, G. B., Dariush, B., & Orin, D. E. (2013). Optimizing foot centers of pressure through force distribution in a humanoid robot. International Journal Humanoid Robotics, 10(3), 1–21. doi:10.1142/S0219843613500278
Yamane, K., & Nakamura, Y. (2009). Comparative study on serial and parallel forward dynamics algorithms for kinematic chains. The International Journal of Robotics Research, 28(5), 622–629.
Acknowledgments
The authors would like the thank the reviewers for their many helpful comments regarding this paper. This work was supported by a National Science Foundation Graduate Research Fellowship to Patrick Wensing, and by Grant No. CNS-0960061 from the NSF with a subaward to The Ohio State University.
Author information
Authors and Affiliations
Corresponding author
Appendix: Validity of the big-ground-inertia approximation
Appendix: Validity of the big-ground-inertia approximation
This section provides a proof that the closed-chain algorithm with the big-ground-inertia approximation computes the correct terms \(\tilde{{\varvec{{\Lambda }}}}_t\), \(\tilde{{\varvec{b}}}_t\), and \({\,\,\tilde{\bar{{\varvec{\!\!J}}}}\, \!{}^T_{\!t}}\) in the limit when the contact inertias \({\varvec{I}}_{c_j}\) become infinite. Throughout this section it is assumed that the floating base for the contact-constrained system has a full 6 degrees of motion freedom. To assist in the proof, \(\tilde{{\varvec{{\Lambda }}}}_{M}\) is defined according to its matrix definition in Eq. 20 and \(\tilde{{\varvec{{\Lambda }}}}_t(\epsilon )\) is defined as the output of the closed-chain algorithm with \({{\varvec{I}}_{c_j} = \epsilon ^{-1} \mathbf{1}}\) for each contact \(j\). It will be shown that
Proof is provided here for \( \tilde{{\varvec{{\Lambda }}}}_t\) since its recursive computation is the simplest algebraically, and proof that the algorithm achieves the correct limits for \(\tilde{{\varvec{b}}}_t\) and \({\,\,\tilde{\bar{{\varvec{\!\!J}}}}\, \!{}^T_{\!t}}\) follows through identical arguments.
While the algorithms thus far have been derived from unconstrained dynamic equations of motion, recursive constrained dynamics can be derived exactly (not approximately as done here for the modified algorithm) using alternative constraint-propagation methods in (Featherstone 2008). These alternative algorithms are composed in terms of inverse inertias, denoted here as \(\,\bar{\!{\varvec{I}}}_i = {\varvec{I}}_i^{-1}\), and articulated inverse inertias \(\,\bar{\!{\varvec{I}}}{}_i^A\).
Although the standard articulated-body equations of motion are only valid when an articulated subsystem has a full 6 degrees of motion freedom, the more general equations
apply when constraints limit motion freedom. In the case that the subsystem rooted at \(i\) has 6 degrees of motion freedom \(\,\bar{\!{\varvec{I}}}_i^A = \left( \,\tilde{\!{\varvec{I}}}{}_i^A\right) ^{-1}\) and Eq. 61 can be rearranged to the articulated inertia relationship used in the main text
At each contact \(c_i\), the constraint that \(\mathbf{a}_{c_i} = -{}^{c_i} \mathbf{a}_{g}\), imposed approximately by Eq. 43, can be imposed exactly selecting \(\,\bar{\!{\varvec{I}}}^A_{c_i} = {\varvec{0}}\) and seeding an inverse inertia recursion with the equation
The articulated-body inertia recursions used in the main text of this paper could then be replaced with analogous recursions on the inverse inertia (Featherstone 2008) that follow
where \({\varvec{\varphi }}_i = {\varvec{{\Phi }}}_i^c\) (the matrix describing the constrained modes of motion for joint \(i\)). While coordinate transformations are omitted in this equation for clarity, they would be required for implementation. These recursions, while more general than the usual articulated-body recursions, are more computationally costly since the quantity
requires a \(5\times 5\) matrix inverse for common revolute joints. The motivation to approximate these recursions through a constraint approximation, is that it allows the use of standard articulated inertia recursions which are more computationally amenable. Recursions for \({\varvec{b}}_i^A\) and \({\varvec{A}}_{ik}\) can be derived analogous to those for \(\,\tilde{\!{\varvec{\beta }}}{}_i^A\) and \(\,\tilde{\!{\varvec{B}}}_{i k}\).
Proof of Eq. 60:
Let \(\,\bar{\!{\varvec{I}}}_{c_j} = \epsilon \mathbf{1}\) for each contact and denote \(\,\bar{\!{\varvec{I}}}_i^A(\epsilon )\) as the final value of \(\,\bar{\!{\varvec{I}}}_i^A\) obtained from the recursions of Eq. 63. In the case when \(\epsilon =0\) the following exact relationship holds
since Eq. 62 imposes an exact constraint at the contact in this case. Additionally when \(\epsilon \ne 0\) the inverse inertia algorithm and the regular inertia algorithm provide equivalent output. That is
Yet, the recursion equation Eq. 63 is comprised of matrix inverses, additions, and multiplies, which are all continuous with respect to their arguments. Thus, all quantities \(\,\bar{\!{\varvec{I}}}_i^A(\epsilon )\) obey
Combination of these relationships provides
where once again the continuity of the matrix inverse of \(\,\bar{\!{\varvec{I}}}_1^A(\epsilon )\) at \(\epsilon =0\) was used in going from line 1 to line 2.
Rights and permissions
About this article
Cite this article
Wensing, P.M., Palmer, L.R. & Orin, D.E. Efficient recursive dynamics algorithms for operational-space control with application to legged locomotion. Auton Robot 38, 363–381 (2015). https://doi.org/10.1007/s10514-015-9420-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10514-015-9420-9