Optimal location of the support of the control for the 1-D wave equation: numerical investigations

Abstract

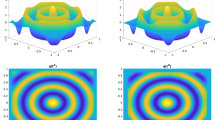
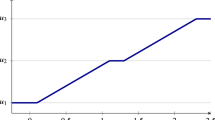
We consider in this paper the homogeneous 1-D wave equation defined on Ω⊂ℝ. Using the Hilbert Uniqueness Method, one may define, for each subset ω⊂Ω, the exact control v _ω of minimal L ²(ω×(0,T))-norm which drives to rest the system at a time T>0 large enough. We address the question of the optimal position of ω which minimizes the functional $J:\omega \rightarrow \|v_{\omega}\|_{L^{2}(\omega \times (0,T))}$ . We express the shape derivative of J as an integral on ∂ ω×(0,T) independently of any adjoint solution. This expression leads to a descent direction for J and permits to define a gradient algorithm efficiently initialized by the topological derivative associated with J. The numerical approximation of the problem is discussed and numerical experiments are presented in the framework of the level set approach. We also investigate the well-posedness of the problem by considering a relaxed formulation.