The functional graph of linear maps over finite fields and applications

Abstract

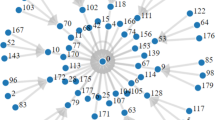
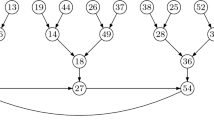
Let $\mathbb F_{q}$ be the finite field with q elements and $n\ge 2$ be a positive integer. We study the functional graph associated to linear maps over finite fields. In particular, we describe the functional graph $\mathcal {G}_f(\mathbb F_{q^n})$ associated to the map induced by $L_f$ on $\mathbb F_{q^n}$, where f is any irreducible divisor of $x^n-1$ over $\mathbb F_q$ and $L_f$ is the q-associate of f. This description derives interesting information on the graph $\mathcal {G}_f(\mathbb F_{q^n})$, such as the number of cycles and the average of the preperiod length. When $\gcd (f, x^n-1)=1$, $L_f$ is a permutation on $\mathbb F_{q^n}$ and the cycle decomposition of $\mathcal {G}_f(\mathbb F_{q^n})$ is well known. In this case, we present some applications of this result, such as the construction of linear involutions over odd characteristic and permutations with few fixed points.