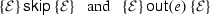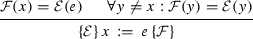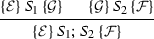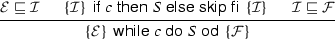Securing a compiler transformation

Abstract

A compiler optimization may be correct and yet be insecure. This work focuses on the common optimization that removes dead (i.e., useless) store instructions from a program. This operation may introduce new information leaks, weakening security while preserving functional equivalence. This work presents a polynomial-time algorithm for securely removing dead stores. The algorithm is necessarily approximate, as it is shown that determining whether new leaks have been introduced by dead store removal is undecidable in general. The algorithm uses taint and control-flow information to determine whether a dead store may be removed without introducing a new information leak. A notion of secure refinement is used to establish the security preservation properties of other compiler transformations. The important static single assignment optimization is, however, shown to be inherently insecure.

Appendices

Appendix

1.1 Hardness of security checking for finite-state programs

Theorem 6

Checking the security of a dead store elimination given as a triple (P, Q, D) is PSPACE-complete for finite-state programs.

Proof

Consider the complement problem of checking whether a transformation from P to Q is insecure. By definition, this is so if there exists a triple (a, b, c) which is leaky for Q but not for P. Determining whether (a, b, c) is leaky can be done in deterministic polynomial space, by simulating the program on the input pairs (a, c) and (b, c). Non-termination is detected in a standard way by adding an n-bit counter, where $2^{n}$ is an upper bound on the size of the search space: the number n is linear in the number of program variables. A non-deterministic machine can guess the triple (a, b, c), then check that the triple is leaky for Q but not leaky for P. Thus, checking insecurity is in non-deterministic PSPACE, which is in PSPACE by Savitch’s theorem.

To show hardness, consider the problem of deciding whether a finite-state program with no inputs or outputs terminates, which is PSPACE-complete by a simple reduction from the IN-PLACE-ACCEPTANCE problem [16]. Given such a program R, let h be a fresh high security input variable and l a fresh low-security state variable, both Boolean, with l initialized to $false$. Define program P as: “$R ;\,l \,:=\,h;\,l \,:=\, false$”, and program Q as: “$R;\,l \,:=\,h$”. As the final assignment to l in P is dead, Q is a correct result of dead store elimination on P. Consider the triple $(h= true ,h= false ,\_)$. If R terminates, then Q has distinct final values for l for the two executions arising from inputs $(h= true ,\_)$ and $(h= false ,\_)$, while P does not, so the transformation is insecure. If R does not terminate, there are no terminating executions for Q, so Q has no leaky triples and the transformation is trivially secure. Hence, R is non-terminating if, and only if, the transformation from P to Q is secure. $\square$

1.2 Hardness of security checking for loop-free finite-state programs

We consider the triple (P, Q, D) which defines a dead store elimination, and ask whether Q is at least as secure as P. We show this is hard, even for the very simple program structure where all variables are Boolean, and assignments are limited to the basic forms $x \,:=\,y$ or $x \,:=\,c$, where x, y are variables and c is a Boolean constant. Some of the variables will be designated as high-security, depending on context.

To simplify exposition, we will use a general assignment of the form $x \,:=\,e$ where e is a Boolean formula. This can be turned into a simple loop-free program of size O(|e|) by introducing fresh variables for each sub-tree of e and turning Boolean operators into if-then-else constructs. (E.g., $x \,:=\,((y\;\vee \;w) \;\wedge \;z)$ is first turned into $t_1 \,:=\,y \;\vee \;w;\, t_2 \,:=\,z;\, x \,:=\,t_1 \;\wedge \;t_2$, then the Boolean operators are expanded out, e.g., the first assignment becomes $\;\mathsf {if}\;y \;\mathsf {then}\;t_1 \,:=\, true \;\mathsf {else}\;t_1 \,:=\,w \;\mathsf {fi}\;$).

Theorem 7

Checking the security of a dead store elimination given as a triple (P, Q, D) is co-NP-complete for loop-free programs.

Proof

Consider the complement problem of checking whether a transformation from P to Q is insecure. Note that P and Q have the same set of low-security variables.

We first show that this problem is in NP. By definition, an insecurity exists if and only if there is a leaky triple (a, b, c) for Q which is not leaky for P. Given a triple (a, b, c) and a program, say P, a machine can deterministically test whether the triple is leaky for P by simulating the pair of executions from (a, c) and (b, c), keeping track of the current low-security state and the last output value for each execution. This simulation takes time polynomial in the program length, as the program is loop-free. A non-deterministic machine can guess a triple (a, b, c) in polynomial time (these are assignments of values to variables), then use the simulation to check first that the triple is not leaky for P and then that it is leaky for Q, and accept if both statements are true. Thus, checking insecurity is in NP.

To show NP-hardness, let $\phi$ be a propositional formula over N variables $x_1,\ldots ,x_N$. Let y be a fresh Boolean variable. Let the x-variables be the low-security inputs, and let y be a high security input. Let z be a low-security variable, which starts at $false$. Define Q(x, y) as the program $z := (\phi \;\wedge \;y)$, and let P(x, y) be the program $Q;\, z := false$. As the final assignment in P is dead, Q is a correct outcome of dead store elimination applied to P. (Note: the programs P and Q may be turned into the simpler form by expanding out the assignment to y as illustrated above, marking all freshly introduced variables as low-security.

Suppose $\phi$ is satisfiable. Let $\overline{m}$ be a satisfying assignment for $\overline{x}$. Define the inputs $(\overline{x}=\overline{m},y= true )$ and $(\overline{x}=\overline{m},y= false )$. In Q, the final value of z from those inputs is $true$ or $false$ depending on value of y, so the triple $t = (y= true ,y= false ,\overline{x}=\overline{m})$ is leaky for Q. However, in P, the final value of z is always $false$, regardless of y, and t is not leaky for P. Hence, the elimination of dead store from P is insecure. If $\phi$ is unsatisfiable then, in Q, the final value of z is always $false$ regardless of y, so the transformation is secure. I.e., the transformation is insecure if, and only if, $\phi$ is satisfiable, which shows NP-hardness. $\square$

1.3 Soundness of the taint proof system

Proposition 2

If $\{\mathcal {E}\}\, {S}\, \{\mathcal {F}\}$ and $\mathcal {E'} \sqsubseteq \mathcal {E}$ and $\mathcal {F} \sqsubseteq \mathcal {F'}$, then $\{\mathcal {E'}\}\, {S}\, \{\mathcal {F'}\}$.

Proof

Consider s, t such that $(s, t) \models \mathcal {E'}$ and ${s}\xrightarrow []{S}{s'}$ and ${t}\xrightarrow []{S}{t'}$.

$\square$

Lemma 7

If $\{\mathcal {E}\}\, {S}\, \{\mathcal {F}\}$, variable x is tainted in $\mathcal {E}$ and S does not modify x, then x is tainted in $\mathcal {F}$.

Proof

(Sketch) Here we prove that $\mathcal {E}(x)$ implies $\mathcal {F}(x)$ by induction on the structure of S. If S is an assignment, this is clearly true by the assignment rule. For a sequence $S_1; S_2$ such that $\{\mathcal {E}\}\, {S_1}\, \{\mathcal {G}\}$ and $\{\mathcal {G}\}\, {S_2}\, \{\mathcal {F}\}$, this is true by the induction hypothesis: $\mathcal {E}(x)$ implies $\mathcal {G}(x)$ which implies $\mathcal {F}(x)$. For a loop, by the inference rule, the loop invariant environment $\mathcal {I}$ must be such that $\mathcal {E}\sqsubseteq \mathcal {I}$, so $\mathcal {I}(x)$ holds. As $\mathcal {I}\sqsubseteq \mathcal {F}$, $\mathcal {F}(x)$ holds. For a conditional, as $\mathcal {E}(x)$ holds by assumption and $\{\mathcal {E}\}\, {S_1}\, \{\mathcal {F}\}$ and $\{\mathcal {E}\}\, {S_2}\, \{\mathcal {F}\}$ hold, by the induction hypothesis, $\mathcal {F}(x)$ holds. $\square$

Theorem 3

Consider a structured program P with a proof of $\{\mathcal {E}\}\, {P}\, \{\mathcal {F}\}$. For all initial states (s, t) such that $(s,t) \models \mathcal {E}$: if ${s}\xrightarrow []{P}{s'}$ and ${t}\xrightarrow []{P}{t'}$, then $(s',t') \models \mathcal {F}$.

Proof

• (0) S is $\mathsf {skip}$ or $\mathsf {out}(e)$:

  

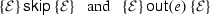
Consider states $s=(m, p)$, $t=(n, q)$, $s'=(m', p')$ and $t'=(n', q')$ such that ${s}\xrightarrow []{S}{s'}$ and ${t}\xrightarrow []{S}{t'}$ hold. By the semantics of $\mathsf {skip}$ and $\mathsf {out}(e)$, $s'=s$ and $t'=t$. Thus, if $(s, t)\models \mathcal {E}$, then $(s', t')\models \mathcal {E}$.

• (1) S is an assignment $x \,:=\,e$:

  

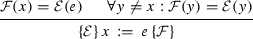
Consider states $s=(m, p)$, $t=(n, q)$, $s'=(m', p')$ and $t'=(n', q')$ such that ${s}\xrightarrow []{S}{s'}$ and ${t}\xrightarrow []{S}{t'}$ hold. By the semantics of assignment, it is clear that $p'=p[x\leftarrow p(e)]$, $q'=q[x\leftarrow q(e)]$, and $m'=n'$ denotes the program location immediately after the assignment. Assume $(s, t)\models \mathcal {E}$, we want to prove $(s', t')\models \mathcal {F}$, or more precisely, $\forall v: \lnot \mathcal {F}(v) \Rightarrow p'(v)=q'(v)$.

Consider variable y different from x. If $\mathcal {F}(y)$ is false, so is $\mathcal {E}(y)$, hence $p(y)=q(y)$ since $(s, t)\models \mathcal {E}$. As $p'(y)=p(y)$ and $q'(y)=q(y)$, we get $p'(y)=q'(y)$ as desired.

Consider variable x. If $\mathcal {F}(x)$ is false, so is $\mathcal {E}(e)$, hence only untainted variables in $\mathcal {E}$ appear in e. As $(s, t)\models \mathcal {E}$, those variables must have equal values in s and t, thus $p(e)=q(e)$. Since $p'=p[x\leftarrow p(e)]$, $q'=q[x\leftarrow q(e)]$, we know $p'(x)=q'(x)$.

• (2) Sequence:

  

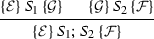
Consider states s and t such that ${s}\xrightarrow []{S_1; S_2}{s'}$ and ${t}\xrightarrow []{S_1; S_2}{t'}$. There must exist intermediate states $s''$ and $t''$ such that ${s}\xrightarrow []{S_1}{s''}$, ${t}\xrightarrow []{S_1}{t''}$, ${s''}\xrightarrow []{S_2}{s'}$ and ${t''}\xrightarrow []{S_2}{t'}$. Now suppose $(s, t)\models \mathcal {E}$, we have:

• (3) Conditional: For a statement S, we use Assign(S) to represent the set of variables assigned in S. The following two cases are used to infer $\{\mathcal {E}\}\, {S}\, \{\mathcal {F}\}$ for a conditional:

  

Let S = $\;\mathsf {if}\;c\;\mathsf {then}\;S_1\;\mathsf {else}\;S_2\;\mathsf {fi}\;$, states $s=(m, p), t=(n, q), s'=(m', p'), t'=(n', q')$. Suppose $(s, t) \models \mathcal {E}$, ${s}\xrightarrow []{S}{s'}$, ${t}\xrightarrow []{S}{t'}$.

Case A: $\mathcal {E}(c)=\text {false}$, hence by definition of $(s, t) \models \mathcal {E}$, we know $p(c) = q(c)$. Thus, both successors $s'$ and $t'$ result from the same branch, say $S_1$. By the hypothesis that $\{\mathcal {E}\}\, {S_1}\, \{\mathcal {F}\}$ and $(s, t) \models \mathcal {E}$, we have $(s', t') \models \mathcal {F}$.

Case B: $\mathcal {E}(c)=\text {true}$, hence $s'$ and $t'$ may result from different branches of S. To show that $(s', t') \models \mathcal {F'}$, let x be a variable untainted in $\mathcal {F'}$. By the definition of $\mathcal {F'}$, there must be no assignment to x in either $S_1$ or $S_2$. Hence, $p'(x)=p(x)$ and $q'(x)=q(x)$.

If $p(x)=q(x)$, then $p'(x)=q'(x)$. Otherwise, consider $p(x)\ne q(x)$, and we show that this cannot be the case. As $(s, t) \models \mathcal {E}$, x must be tainted in $\mathcal {E}$. As x is not modified in $S_1$ and $\{\mathcal {E}\}\, {S_1}\, \{\mathcal {F}\}$ holds, by Lemma 7 (below), x is tainted in $\mathcal {F}$. Since $\mathcal {F}\sqsubseteq \mathcal {F'}$, x is tainted in $\mathcal {F'}$, which is a contradiction. Hence, we show that $p'(x)=q'(x)$ for any variable x untainted in $\mathcal {F'}$. Clearly, $m'=n'$, thus $(s', t') \models \mathcal {F'}$.

• (4) While Loop:

  

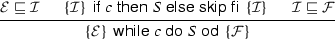
Let states s, t be such that $(s, t) \models \mathcal {E}$, and $s', t'$ be the states reached from s, t at the end of the while loop. By $\mathcal {E}\sqsubseteq \mathcal {I}$, $(s, t) \models \mathcal {I}$. We want to prove that $(s', t') \models \mathcal {I}$, so that by $\mathcal {I}\sqsubseteq \mathcal {F}$, we can have $(s', t') \models \mathcal {F}$.

Let the trace from s to $s'$ be $s=s_0, s_1, \ldots , s_n=s'$ where $s_i$ are states at the start of successive loop iterations. Similarly, let the trace from t to $t'$ be $t=t_0, t_1, \ldots , t_m=t'$. Without loss of generality, assume that $n > m$, then we can pad the t-trace with sufficiently many $\mathsf {skip}$ actions (i.e., the same as “$\;\mathsf {if}\;c\;\mathsf {then}\;S\;\mathsf {else}\;\mathsf {skip}\;\mathsf {fi}\;$” where the evaluation of c is false) to make the two traces of the same length. The final state of padded t-trace is still $t'$. For the rest of proof, we assume that $n = m$ and prove by induction on n that $(s_i, t_i) \models \mathcal {I}$.

The induction basis $(s_0=s, t_0=t) \models \mathcal {I}$ holds. Then, assume the claim that for $k\ge 0$, $(s_k, t_k) \models \mathcal {I}$. From the hypothesis “$\{\mathcal {I}\}\, {\;\mathsf {if}\;c\;\mathsf {then}\;S\;\mathsf {else}\;\mathsf {skip}\;\mathsf {fi}\;}\, \{\mathcal {I}\}$” of the inference rule, we get $(s_{k+1}, t_{k+1}) \models \mathcal {I}$ as well. Hence, $(s'=s_n, t'=t_m) \models \mathcal {I}$ holds. $\square$

Taint analysis for control-flow graphs

In this section, we describe how to adjust the taint proof system to apply to control-flow graphs (CFGs). We assume that a control-flow graph has a single entry node and a single exit node. A program is defined by its control flow graph, which is a graph where each node is a basic block and edges represent control flow. A basic block is a sequence of assignments to program variables.

The entry and exit nodes are special. All other nodes fall into one of three classes. The partitioning makes it easier to account for taint values and propagation.

• A merge node has multiple incoming edges and a $\phi$ function $x \leftarrow \!\phi \!((x_1,e_1), \ldots , (x_n,e_n))$ for every variable x, which (simultaneously over all variables) assigns x the value of $x_1$ if control is transferred through edge $e_1$, the value of $x_2$ if control is transferred through edge $e_2$ and so forth,

• A basic node, which is a single assignment statement, and

• A branch node, which is either an unconditional branch to the following node, or a conditional branch on condition c, through edge $e_t$ if c is true, and through edge $e_f$ if c is false.

The edge relations are special. The entry node has a single merge node as a successor and no incoming edge. The exit node has itself as the single successor, and behaves like a $\mathsf {skip}$. Every merge node has a single successor, which is a basic node. Every basic node has a single successor, which is either a basic or a branch node. Every successor of a branch node is either a merge node or the exit node.

A taint annotation for a control-flow graph is an assignment of environments to every CFG edge. An annotation is valid if the following conditions hold:

• The assignment to the outgoing edge from the entry node has high-security input variables set to H ($true$) and all other variables set to L ($false$),

• For a merge node with assignments $x \leftarrow \phi ((x_1,e_1), \ldots , (x_n,e_n))$, incoming edges annotated with $\mathcal {E}_1,\ldots ,\mathcal {E}_n$ and outgoing edge annotated with $\mathcal {F}$, for all i: $\{{\mathcal {E}_i}\} {x \leftarrow x_i} \{{F}\}$ holds. Note that here all $\phi$ assignments are gathered into one to keep the notation simple,

• For a basic node with assignment statement S, incoming edge annotated with $\mathcal {E}$ and outgoing edge annotated with $\mathcal {F}$, the assertion $\{{\mathcal {E}}\} {S} \{{\mathcal {F}}\}$ holds,

• For an unconditional branch node with incoming edge annotated with $\mathcal {E}$ and outgoing edge annotated with $\mathcal {F}$, $\{{\mathcal {E}}\} {\mathsf {skip}} \{{\mathcal {F}}\}$ holds, and

• For an conditional branch node $\;\mathsf {if}\;c\;\mathsf {then}\;e_t \;\mathsf {else}\;e_f \;\mathsf {fi}\;$, with incoming edge annotated with $\mathcal {E}$ and outgoing edges annotated with $\mathcal {F}_t$ and $\mathcal {F}_f$, respectively:

  • $\{{\mathcal {E}}\} {\mathsf {skip}} \{{\mathcal {F}_t}\}$ and $\{{\mathcal {E}}\} {\mathsf {skip}} \{{\mathcal {F}_f}\}$ hold, and

  • If $\mathcal {E}(c)$ is true (i.e., c is tainted in $\mathcal {E}$), then let d be the the immediate post-dominator for this branch node. Node d must be a merge node, say with incoming edges $f_1,\ldots ,f_k$. Let $\mathcal {F}_1,\ldots ,\mathcal {F}_k$ be the environments assigned, respectively, to those edges. Let $\mathsf {Assign}(n,d)$ be an over-approximation of the set of variables assigned to on all paths from the current branch node n to d. Then, for all $x \in \mathsf {Assign}(n,d)$, and for all i: it must be the case that $\mathcal {F}_i(x)= true$.

A structured program turns into a control flow graph with a special (reducible) structure. It is straightforward to check that a valid structured proof annotation turns into a valid CFG annotation for the graph obtained from the structured program.

1.1 Soundness

We have the following soundness theorem. Informally, the theorem states that if (the node from) edge f post-dominates (the node from) edge e, then computations starting from states consistent with e’s annotation to f result in states which are consistent with f’s annotation. It follows that terminating computations starting from states consistent with the entry edge annotation result in states consistent with the exit edge annotation. We write ${(s,e)} {\mathop {\longrightarrow }\limits ^{p}} {(s',f)}$ to indicate that there is a path (a sequence of edges $e_0=e,e_1,\ldots ,e_k=f$ such that the target of $e_{i}$ is the source of $e_{i+1}$, for all i) from e to f, and that $s'$ at edge f is obtained from state s at edge e by the actions along that path.

Theorem 8

For a given CFG: let e be an edge incident on node n, and let f be an outgoing edge from node m which post-dominates n. Let $\mathcal {E}, \mathcal {F}$ be the annotations for edges e and f, respectively. For states s, t such that $(s,t) \models \mathcal {E}$ and states u, v and paths p, q such that ${(s,e)} {\mathop {\longrightarrow }\limits ^{p}} {(u,f)}$ and ${(t,e)} {\mathop {\longrightarrow }\limits ^{q}} {(v,f)}$, it is the case that $(u,v) \models \mathcal {F}$.

Proof

The proof is by induction on the sum of the lengths of paths p and q, where the length is the number of edges on the path.

The base case is when the sum is 2. Then $m=n$, and f is an outgoing edge of node n. The validity conditions ensure that $\{{\mathcal {E}}\} {S} \{{\mathcal {F}}\}$ hold, where S is the statement associated with n. It follows that $(u,v) \models \mathcal {F}$.

Assume inductively that the claim holds when the sum is at most k, for $k \ge 0$. Now suppose the sum is $k+1$. The argument goes by cases on the type of node n.

• (1) n is a merge node, a basic node, or an unconditional branch node. Then it has a single successor node, say $n'$, via some edge $e'$. Let $\mathcal {E'}$ be the annotation on $e'$. By the conditions on a valid annotation, $\{{\mathcal {E}}\} {S} \{{\mathcal {E'}}\}$ holds, where S is the statement associated with n. Thus, for the immediate successors $s',t'$ of s, t along the paths p, q (respectively), $(s',t') \models \mathcal {E'}$. As $n'$ is the immediate post-dominator of n and all post-dominators of n are linearly ordered, m is a post-dominator of $n'$. The suffixes $p',q'$ of the paths p, q starting at $e'$ have smaller total length. By the induction hypothesis, as $(s',t') \models \mathcal {E'}$, it follows that $(u,v) \models \mathcal {F}$.

• (2) n is a conditional branch node with condition c and successor edges $e_t,e_f$ leading to successor nodes $n_t,n_f$. There are two cases to consider.

• (2a) The branch condition is tainted, i.e., $\mathcal {E}(c)= true$. Let $n'$ be the immediate post-dominator of n. This must be a merge node by the canonical structure of the CFG, with a single outgoing edge, say $g'$. By the constraints on valid annotation, if $\mathcal {G}$ is the annotation on $g'$, then $\mathcal {G}(x)= true$ if variable x is assigned to on a path from n to $n'$. Hence, if $\mathcal {G}(x)= false$, then x has no assignment on such a path, in particular, it has no assignment on the segments $p'$ of p and $q'$ of q from n to the first occurrence of $n'$. Let $s',t'$ be the states after execution of $p'$ and $q'$ (resp.). Then, $s'(x)=s(x)$ and $t'(x)=t(x)$. By the contrapositive of Lemma 7, $\mathcal {E}(x)= false$. As $(s,t) \models \mathcal {E}$, it follows that $s(x)=t(x)$ and, therefore, $s'(x)=t'(x)$. This shows that $(s',t') \models \mathcal {G}$. As the suffixes $p'',q''$ of the paths p, q after $n'$ have smaller total length, and m is a post-dominator of $n'$ (recall that all post-dominators of n are linearly ordered and $n'$ is the first), from the induction hypothesis, it follows that $(u,v) \models \mathcal {F}$.

• (2b) The branch condition is untainted, i.e., $\mathcal {E}(c)= false$. Thus, $s(c)=t(c)$, so the paths p, q have a common successor, say $n_t$, through edge $e_t$. The validity conditions imply that $\{{\mathcal {E}}\} {\mathsf {skip}} \{{\mathcal {E}_t}\}$ hold, where $\mathcal {E}_t$ is the annotation for edge $e_t$. Hence, $(s,t) \models \mathcal {E}_t$. As m is a post-dominator of n, it is also a post-dominator of $n_t$. The suffixes $p',q'$ of p, q from $n_t$ have smaller total length; hence, by the induction hypothesis, $(u,v) \models \mathcal {F}$.$\square$