Filtering methods for content-based retrieval on indexed symbolic music databases

Abstract

We introduce fast filtering methods for content-based music retrieval problems, where the music is modeled as sets of points in the Euclidean plane, formed by the (on-set time, pitch) pairs. The filters exploit a precomputed index for the database, and run in time dependent on the query length and intermediate output sizes of the filters, being almost independent of the database size. With a quadratic size index, the filters are provably lossless for general point sets of this kind. In the context of music, the search space can be narrowed down, which enables the use of a linear sized index for effective and efficient lossless filtering. For the checking phase, which dominates the overall running time, we exploit previously designed algorithms suitable for local checking. In our experiments on a music database, our best filter-based methods performed several orders of a magnitude faster than the previously designed solutions.

1 Introduction

In this paper we are interested in content-based music retrieval (CBMR) of symbolically encoded music. Such setting enables searching for excerpts of music, or occurrences of query patterns, that constitute only a subset of instruments appearing in the full orchestration of a musical work. Instances of the setting include the well-known query-by-humming application, but our framework can also be used for more complex applications where the query pattern searched for and the music database to be searched may be polyphonic. Examples of such applications include musicological analysis of lengthy musical works (e.g. operas) where polyphonic patterns could be efficiently identified without the burden of handicraft, and music clustering based on a given set of polyphonic profiles.

Another example of a complex application, where the CBMR framework could be used as a tool, is plagiarism detection: consider a new music piece that is to be inspected for plagiarism. One can extract (manually) some set of significant melody passages from the piece and search for them in a database of existing symbolically encoded music. The matching pieces in the database can be sorted according to the frequency of matches of the chosen melody passages (or with some more elaborate metric), and the inspector can then manually check the most distinguishing candidates. For the approach to be successful, the CBMR algorithm should be effective enough to detect similar melody passages and omit dissimilar ones, and fast enough to enable real time queries.

Indeed, the design of a suitable CBMR algorithm is always a compromise between effectiveness and efficiency. Effectiveness means high precision and recall: the similarity/distance measure used by the algorithm should not be too permissive to detect false matching positions (giving low precision) and not too restrictive to omit true matching positions (giving low recall). In this paper, we concentrate on a modeling of music that we believe is effective in this sense, and at the same time provides computationally feasible retrieval performance.

As symbolically encoded monophonic music can easily be represented as a linear string, in literature several solutions for monophonic CBMR problems are based on an appropriate method from the string matching framework (see e.g. Ghias et al. 1995; Mongeau and Sankoff 1990). Polyphony, however, imposes a true challenge, especially when no voicing information is available (i.e., for a note it is not known for which voice it belongs to, thus preventing the possibility for an effective string representation), or the occurrence is allowed to be distributed across the voices (Lemström and Pienimäki 2007). In some cases it may suffice to use some heuristic, as for an example the SkyLine algorithm (Uitdenbogerd and Zobel 1998), to achieve a monophonic reduction out of the polyphonic work. This, however, does not often provide musically meaningful results.

In order to be able to deal with polyphonic music, geometric-based modeling has been suggested (Clausen et al. 2000; Typke 2007; Ukkonen et al. 2003; Wiggins et al. 2002). Most of these provide also another useful feature, i.e., extra intervening elements in the musical work, such as grace notes, that do not appear in the query pattern can be ignored in the matching process. The downside is that the geometric online algorithms (Clifford et al. 2006; Lubiw and Tanur 2004; Ukkonen et al. 2003; Wiggins et al. 2002) are not computationally as efficient as their counterparts in the string matching framework. Moreover, the known offline (indexing) methods (Clausen et al. 2000; Typke 2007) compromise on crucial matters.

These downsides are not surprising: the methods look at all the subsequences and the number of them is exponential in the length of the database. Thus, a total index would also require exponential space.

In this paper we deal with symbolically encoded, polyphonic music for which we use the pitch-against-time representation of note-on information, as suggested in Wiggins et al. (2002) (see Figs. 1 and 2). The musical works in a database are concatenated in a single geometrically represented file, denoted by $T; T=t_1, t_2, {\ldots,}t_n,$ where $t_j \in {\mathbb{R}}^2$ for 1 ≤ j ≤ n. In a typical retrieval case the query pattern $P, P=p_1, p_2, \ldots, p_m; p_i \in {\mathbb{R}}^2$ for 1 ≤ i ≤ m, to be searched for is often monophonic and much shorter than the database T to be searched, that is m ≪ n. We assume that P and T are given in the lexicographic order. If this is not the case, the sets can be sorted in mlogm and nlogn times, respectively.¹

Fig. 1

An excerpt of Einojuhani Rautavaara’s opera Thomas (1985). Printed with the permission of the publisher Warner/Chappell Music Finland Oy

Fig. 2

Pointset T, to the left, represents Fig. 1 in the geometric representation. Pointset P, to the right, corresponds to the first two and half bars of the melody line (the highest staff of Fig. 1) but the fifth point has been delayed somewhat. The depicted vectors correspond to translation f that gives the largest partial match of P within T

The problems of interest are the following:

• (P1) Find translations of P such that each point in P match with a point in T.

• (P2) Find translations of P that give a partial match of the points in P with the points in T.

• (P2′) Find translations of P that give a partial match of the points in P with the points in T, such that each point in a marked point subset P ^m (P ^m ⊂ P) match with a point in T.

Notice that the partial matches of interest in P2 need to be defined properly, e.g. one can use a threshold k to limit the minimum size of partial matches of interest. Alternatively, one can search for the partial matches of maximal size only. The algorithms discussed in the sequel work for both versions if not otherwise mentioned.

Problem P2′ is a modified version of P2 in which the user may declare points that are important and have to be present in a match. This setting is relevant in cases where the user may be able to say which out of his hummed notes were correct but is not capable of correcting the possibly false ones.

Ukkonen et al. (2003) presented algorithms PI and PII solving problems P1 and P2 in worst case times O(mn) and O(mnlogm), respectively. Their algorithms require O(m) space. Noteworthy, the algorithm solving P1 has an O(n) expected time complexity. Clifford et al. (2006) showed a connection of P2 to a problem family for which o(mn) solutions are conjectured not to exist, and give an approximation algorithm, called MsM, for P2, that runs in time O(nlogn).

In this paper we introduce index-based filtering algorithms for the three problems presented above. Our contribution is twofold. Firstly, our methods outperform their competitors; in particular, the algorithms are output sensitive, i.e., the running time depends more on the output than on the input. This is achieved by exploiting a simple indexing structure that is not a total index. Secondly, we show how to keep the index of a practical, linear size. The index enables fast filtering; the running time of the filters can be expressed as $O(g_f(m){\log}n+i_f),$ where $i_f{\leq}n$ is the number of intermediate positions the filter f examines in order to produce c _f candidate positions, and g _f (m) is a function specific to filter f. The found $c_f (c_f{\leq i_f\leq}n)$ candidate positions are subsequently checked using Ukkonen et al’s PI and PII algorithms. Thus, executing checking take time O(c _f m) and O(c _f mlogm), in the worst case, for P1 and P2, respectively. It happens that the more complicated the filter is, the larger g _f (m) is, yet i _f and c _f get smaller. This tradeoff in the filters is studied experimentally.

2 Related work

We will denote by P + f a translation of P by vector f, i.e., vector f is added to each component of P separately: $P+f=p_1+f, p_2+f, {\ldots,}p_m+f.$ Problem P1 can then be expressed as the search for a subset I of T such that P + f = I for some f. Please note that a translation corresponds to two musically distinct phenomena: a vertical move corresponds to transposition while a horizontal move corresponds to aligning the pattern time-wise (see Fig. 2).

It is easy to solve P1 in O(mn log(mn)) time: collect all translations mapping each point of P to each point of T, sort the set based on the lexicographic order of the translation vectors (see below for definition), and report the translation getting most votes (i.e. being most frequent). If some translation f gets m votes, then a subset I of T is found such that P + f = I. With some care in organizing the sorting, one can achieve O(mn logm) time (Ukkonen et al. 2003). The voting algorithm also solves the P2 problem under translations.

A faster algorithm specific to P1 is as follows: Let $p_1,p_2, \ldots ,p_m$ and $t_1,t_2, \ldots , t_n$ be the lists of pattern and database points, respectively, lexicographically ordered according to their 2-dimensional coordinate values: $p_{i}\,<\,p_{i+1}$ iff $p_{i}.x \,<\, p_{i+1}.x$ or ($p_{i}.x=p_{i+1}.x$ and $p_{i}.y \,< \,p_{i+1}.y$), and $t_{j} < t_{j+1}$ iff $t_{j}.x < t_{j+1}.x$ or ($t_{j}.x=t_{j+1}.x$ and $t_{j}.y < t_{j+1}.y$), where .x and .y denote the two coordinates. Consider the translation $f_{i_{1}}=t_{i_{1}}-p_1,$ for any $1\leq i_1 \leq n.$ One can scan the database points in the lexicographic order to find a point $t_{i_{2}}$ such that $p_2+f_{i_{1}}=t_{i_{2}}.$ If such is found, one can continue scanning from $t_{{i_{2}}+1}$ on to find $t_{i_{3}}$ such that $p_3+f_{i_{1}}=t_{i_{3}}.$ This process is continued until a translated point of P does not occur in T or until a translated occurrence of the entire P is found. The resulting procedure is given in Fig. 3.

Fig. 3

Algorithm 1

The properties of the above solutions are summarized below.

Theorem 1 (Ukkonen et al. 2003)

The P1 problem under translations for query pattern P and database T can be solved in O(mn) time and O(m) working space where m = |P| ≤ |T| = n.

For P2 the O(mn logm) time voting algorithm is still the fastest known. However, it is known that quadratic running times are probably the best one can achieve for this problem:

Theorem 2 (Clifford et al. 2006)

The P2 problem is 3SUM -hard.

This means that an o(|P||T|) time algorithm for P2 would yield an o(n ²) algorithm for the 3SUM problem, where |T| = n and |P| = Θ(n). The 3SUM problem asks, given n numbers, whether there are three numbers a, b, and c among them such that a + b + c = 0; finding a sub-quadratic algorithm for 3SUM would be a surprise (Barequet and Har-Peled 2001).

The 3SUM -hardness result has an implication on the possibility of finding good indexing solutions to P2: it is 3SUM -hard to build an index structure for T in g(n) time so that one could later solve P2 in h(m) time, where g(n) + h(m) = o(n ²). To see why this holds, notice that for patterns of length Θ(n), one could otherwise solve P2 in o(n ²) time. Hence, either the preprocessing time g(n) or online query time h(m) need to be quadratic under the 3SUM -hardness assumption.

Clausen et al. (2000) suggested an indexing schema to be used with the geometric representation. Their aim was to achieve sublinear query times in the length of the score. This is achieved using an indexing schema similar to inverted files for natural language Information Retrieval. The efficiency is achieved with the cost of robustness. The indexing alters the original database converting it into an invariant form, so that if the same processing is done for the pattern, one can find the occurrences quickly. This information extraction however makes the approach non-applicable to problems P1 and P2 as exact solution.

Another very general indexing approach has been proposed recently (Typke 2007). Typke proposes the use of metric indexes. This approach has the advantage that it works under robust geometric similarity measures. However, the disadvantage is that it is difficult to support translations or partial matching; the approach assumes that the database contains the essential parts of each musical work, such that the query can directly be compared against an extract from the corresponding work.

We will confine to an approach that combines indexing and practically lossless filtering. That is, we study solutions to P1, P2, and P2′ that do some preprocessing for the database. This preprocessing builds an index for the database that can be used to speed up a filtering algorithm: such an algorithm tries to find all promising areas in the database where the real occurrences could lie. Filtering algorithm is lossless if no real occurrence is missed by the filter; to this end we use special characteristics of the considered applications. The other objective is to minimize the amount of false positives, i.e., areas where, after checking, no real occurrences could be found. Such algorithms are widely studied in the context of approximate string matching; for background on filtering, see Navarro (2001).

Our filters have close counterparts in the string matching domain; namely the pattern matching with gaps (Crochemore et al. 2002), with transposition invariance added (Mäkinen et al. 2005; Fredriksson et al. 2006), gives similar problem statement to that of ours. The difference is due to the discrepancy in the modelling of music: string representation omits the time information of the point set representation. Hence, the algorithms working on the string representation may allow spurious matches where the rhythmic characteristics can be arbitrarily far away from that of the pattern. In practice, as this difference is not that dramatic we will therefore compare our filters to the best current algorithms (Fredriksson and Grabowski 2008) obtained for the string representation.²

3 Index based filters

The idea used in Ukkonen et al. (2003) and Wiggins et al. (2002) is to work on trans-set vectors. Let p ∈ P be a point in the query pattern. A translation vector f is a trans-set vector, if there is a point t ∈ T, such that p + f = t. Let the number of points in P and T be m and n, respectively. Moreover, without loss of generality, let us assume all the points both in the pattern and in the database to be unique. So, the number of (unique) trans-set vectors is within the range [n + m − 1, nm], i.e., quadratic in the worst case.

For the indexing purposes we consider translation vectors that appear within the pattern and the database. We call translation vector f intra-pattern vector, if there are two points p and p′, where p, p′ ∈ P, such that p + f = p′. The intra-database vector is defined in the obvious way. The number of intra-pattern and intra-database vectors are O(m ²) and O(n ²), respectively.³

A nice property of Ukkonen et al’s PI and PII algorithms is that they are capable of starting the matching process anywhere in the database. Should there be a total of s occurrences of the pattern within the database and an oracle telling where they are, we could check the occurrences in O(sm) and O(smlogm) time, in the worst case, by executing locally PI and PII, respectively.

In the sequel we will exploit this property by first running a filtering algorithm whose output is subsequently checked, depending on the case, by PI or PII. If a quadratic size for the index structure is allowed, we have a lossless filter: all intra-database vectors are stored in a balanced search tree in which each translation can be retrieved in O(logn) time.

Definition 1

C(f) is the list of starting positions i of vector $f=t_j-t_i,$ for some j, in the database.

Such lists are stored as leaves of a binary search tree so that a search from root with key f leads to the associated leaf (see Fig. 4). Let us denote by |C(f)| the number of elements in the list. Since the points are readily in the lexicographic order, building such a structure takes a linear time in the number of elements to be stored.

Fig. 4

The dataset T and the corresponding search tree when α = 4. We have suppressed the subtrees that are not of interest when also the pattern P (bottom left corner) is given

However, for large databases, a quadratic space is infeasible. To avoid that, we store only a subset of the intra-database vectors. In content-based music retrieval, where the query pattern is typically given by humming or by playing an instrument, an occurrence is not scattered throughout the database, but is a very local and compact subpart of the database typically not including too many intervening elements. Now we make a full use of this locality and that the points are readily sorted: for each point i in the database, 1 ≤ i ≤ n − 1, we store intra-database vectors to points $i+1, \ldots, i+\alpha+1$ ($\alpha = \min (\alpha,n-i-1)$), where α is a constant, independent of n and m. Constant α sets the ‘reach’ for the translation vectors. Thus, the index structure becomes of linear, O(n) size. Naturally such filters are no more totally lossless, but by choosing a large α and by careful thinking in the filtering algorithms, losses are truly minimal.

As for an example, consider the case given in Fig. 4. Here n = 12 and we have chosen α = 4, which gives us, instead of (12 × 11)/2 = 66, 43 translation vectors out of which 23 are original. So, each original vector f appears as a label of a leaf and is followed by a list C(f) giving the starting positions of such vector f in T. Note, for instance, that t ₅ at position 〈3, 4〉 does not appear in the list for translation vector 〈4, 0〉 although $t_5 + \langle 4,0 \rangle = \langle 7,4 \rangle = t_{11} \in T,$ because it does not fit in the window (11 − 5 > α + 1).

In the following, we develop eight lossless filters {Filter K}, $k \in \{0,1,\ldots ,7\},$ all sharing the same structure:

• Select candidate positions Examine some intra-pattern vectors f and their starting positions C(f) in the database. This step takes O(g _k (m)logn + i _k ) time, where g _k () is a function depending on FilterK and i _k is the amount of intermediate candidate positions, i.e, the number of the starting positions examined to produce the final set of candidates of size c _k .

• Check candidates Use algorithm PI or PII locally to check the candidate positions for real occurrences in time O(mc _k ) or O(mc _k logn), respectively.

All the filters are lossless: the c _k candidate positions contain all the s real occurrences. The goal is to minimize c _k , yet, keeping the running time O(g _k (m)logn + i _k ) of the selection process reasonable. This creates a tradeoff, which we try to cover with the eight choices for the filter.

3.1 Solving P1

To solve the problem P1 we consider four straightforward filters. The simplicity of these filters is due to the fact that all the points (and therefore all the intra-pattern vectors) need to find their counterparts within the database. Thus, to find candidate occurrences, we may consider occurrences of any of the intra-pattern vectors.

In Filter0 we choose a random intra-pattern vector f = p _j  − p _i . The candidate list to be checked is C(f) containing thus c ₀ = |C(f)| candidates. For Filter1 and Filter2 we collect statistics about the frequency of distinct intra-database vectors. Filter1 chooses the intra-pattern vector $f^{\ast}=p_j-p_i$ that occurs the least in the database, i.e., for which the $c_1=|C(f^{\ast})|$ is smallest. In Filter2, we consider the two intra-pattern vectors $f^{\ast}=p_j-p_i$ and $f^{\ast\ast}=p_l-p_k$ that have the least occurrences within the database, i.e., for which $i_2=|C(f^{\ast})|+|C(f^{\ast\ast})|$ is smallest (see Fig. 4). Then the set

$$ S=\left\{i^{\prime\prime} \mid t_{i^{\prime}}-t_{i^{\prime\prime}}=p_i-p_1, i^{\prime} \in C(f^{\ast}), t_{k^{\prime}}-t_{i^{\prime\prime}}=p_k-p_1, k^{\prime} \in C(f^{\ast\ast})\right\} $$

(1)

contains the candidates for starting positions of the pattern, such that both $f^{\ast}$ and $f^{\ast\ast}$ are included in each such occurrence.

For instance, consider the example depicted in Fig. 4. Let us assume that the two illustrated intra pattern vectors are selected by the algorithm. Then we know that $p_i=p_2=\langle 2,3 \rangle;\,p_k = p_1=\langle 1,1 \rangle;\,f^{\ast}=\langle 2,-1 \rangle;\,C(f^{\ast})=\{\langle 3,4 \rangle, \langle 4,6 \rangle \};\,f^{\ast\ast}=\langle 4,0 \rangle;$ and $C(f^{\ast\ast})=\{\langle 2,2 \rangle,\langle 2,5 \rangle \}.$ Now the candidate positions are given by the Eq. 1:

$$ S = \left\{i^{\prime\prime} \mid t_{i^{\prime}}-t_{i^{\prime\prime}}=p_i-p_1, i^{\prime} \in C(f^{\ast}),t_{k^{\prime}}-t_{i^{\prime\prime}}=p_k-p_1, k^{\prime} \in C(f^{\ast\ast})\right\} $$

(2)

$$ = \left\{i^{\prime\prime} \mid t_{i^{\prime}}-t_{i^{\prime\prime}}=\langle 1,2 \rangle, i^{\prime} \in \{ \langle 3,4 \rangle, \langle 4,6 \rangle \}, t_{k^{\prime}}-t_{i^{\prime\prime}}=\langle 0,0 \rangle, k^{\prime} \in \{ \langle 2,2 \rangle, \langle 2,5 \rangle\} \right\} $$

(3)

$$ = \left\{i^{\prime\prime} \mid \{t_5-t_{i^{\prime\prime}}=\langle 1,2 \rangle, t_6-t_{i^{\prime\prime}}=\langle 1,2 \rangle \} \land \{t_3-t_{i^{\prime\prime}}=\langle 0,0 \rangle, t_4-t_{i^{\prime\prime}}=\langle 0,0 \rangle\} \right\} $$

(4)

$$ =\left\{i^{\prime\prime} \mid \{t_{i^{\prime\prime}}=t_3 \lor t_{i^{\prime\prime}}=t_5\} \land \{t_{i^{\prime\prime}}=t_3 \lor t_{i^{\prime\prime}}=t_4\}\right\} $$

(5)

$$ = \{3,5\} \bigcup \{3,4\} $$

(6)

$$ = \{3\} $$

(7)

Note that after line 3 we know that $t_{\langle 3,4 \rangle}=t_5; t_{\langle 4,6 \rangle}=t_6; t_{\langle 2,2 \rangle}=t_3; {\hbox {and}} \; t_{\langle 2,5 \rangle} = t_4.$

Thus, given the window length α = 4, in this case we have found only one candidate to be checked that resides at position t ₃.

For the running time, Filter0 uses O(logn) time to locate the candidate list. Filter1 and Filter2 execute at most O(m ²) additional inquiries each taking O(logn) time. Filter2 needs also O(i ₂) time for intersecting the two occurrence lists into the candidate list S, with i ₂ = |S|; notice that values i″ can be scanned from left to right simultaneously to the scanning of lists C($f^{\ast}$) and C($f^{\ast\ast}$) from left to right, taking amortized constant time at each step of the intersection.

With all the filters we could consider only translations between consecutive points within the pattern. In this way we would somewhat compromise on the potential filtration power, but the ‘reach constant’ α above would get an intuitive interpretation: it tells how many intervening points are allowed to be in the database between any two points that match with the consecutive pattern points.

For long patterns, the search for the intra-pattern vector that occurs the least in T may dominate the running time. Hence, we have Filter3 that is Filter2 with a random set of intra-pattern vectors as the input.

The correctness (losslessness) of these four filters follows directly from their derivations.

3.2 Solving P2

The same preprocessing as above is used for solving P2, but the search phase needs to be modified in order to find partial matches. We will concentrate on the case where a threshold k is set for the minimum size of a partial match. Since any pattern point can be outside the partial match of interest, one could in principle check the existence of all the O(m ²) vectors among the intra-database vectors, store these candidate positions in a multiset S, and run the checking on each candidate position in S with algorithm PII. More formally, the multiset S contains position i″ for each intra-pattern vector f = p _j  − p _i such that i′ ∈ C(f) and $p_{i}-p_{1}=t_{i^{\prime}}-t_{i^{\prime\prime}}.$ ⁴ However, this basic filter can be trivially sped up by noticing that sorting the multiset S implements the voting algorithm; if a candidate position i″ occurs at least k times in S, then it is a real occurrence and no more testing with PII is necessary. For fluency reasons, we call this lossless filter Filter4, although it is in fact directly a solution to P2. We will also consider a lossy variant Filter5, where for each pattern point p only one half of the intra-pattern vectors (those that are least frequent in the database) having p as an endpoint is chosen. Let i ₄ and i ₅ be the number of candidate positions in S for the two filters, the running times become O(m ²logn + i ₄logm) and O(m ²logn + i ₅logm), respectively, since the required sorting phase can be implemented by merging the O(m ²) ordered lists.

The pigeon hole principle can be used to reduce the amount of intra-pattern vectors to check: if the pattern is split into (m − k + 1) distinct subsets, then at least one subset must be present in any partial occurrence of the complete pattern. Therefore, it is enough to run the filters derived for P1 on each subset independently and then check the complete set of candidates. The total amount of intra-subset vectors is bound by $O((m-k+1)(\frac{m} {m-k+1})^2)=O(\frac{m^2} {m-k+1}).$ This is O(m) whenever k is chosen as a fraction of m. The filters Filter0–Filter2 each select constant number of vectors among each subset, so the total number of candidate lists produced by each filter is O(m − k + 1). Hence, this way the filtration efficiency (number of candidates produced) seems to depend linearly on the number of errors m − k allowed in the pattern. This is an improvement to the trivial approach of checking all O(m ²) intra-pattern vectors.

Notice that these pigeon hole filters are lossless if all the intra-database vectors are stored. However, the approach works only for relatively small error-levels, as each subset needs to contain at least two points in order to make filtering possible. Let us focus on how to optimally use Filter1 for the subsets in the partition, as Filter0 and Filter2 are less relevant for this case. The splitting approach gives the freedom to partition the pattern into subsets in an arbitrary way. For optimal filtering efficiency, one should partition the pattern so that the sum of least frequent intra-subset vectors is minimized. This sub-problem can be solved by finding the minimum weight maximum matching in the graph whose nodes are the points of P, edges are the intra-pattern vectors, and edge weights are the frequencies of the intra-pattern vectors in the database. In addition, a set of dummy nodes are added each having an edge of zero weight to all pattern points. These edges are present in any minimum weight matching, so their amount can be chosen so that the rest of the matched edges define the m − k non-intersecting intra-pattern vectors whose frequency sum is minimum. Figure 5 illustrates the reduction.

Fig. 5

Reducing pattern splitting into minimum weight maximum matching with m = 5 and k = 4 (i.e. k = m − 1). The numbered points represent the nodes created from pattern; the 6th point is the added dummy node. Dashed edges are drawn between each pair of nodes, and their weights (frequencies) are listed to the right of the graph. The optimal matching (solid edges) covering all nodes induces two intra-pattern vectors and one dummy edge. These intra-pattern vectors are the two (= (m − k + 1)) distinct vectors whose summed frequency in the database is minimum, and hence provide the best filtration efficiency for the splitting strategy

We use an O(m ³) time minimum weight maximum matching algorithm to select the m − k + 1 intra-pattern vectors in our filter. Some experiments were also done with an O(m ²) time greedy selection. We call this algorithm Filter6 in the experiments.

Since Filter6 is the most advanced of the filters, we give its pseudocode (Fig. 6) and prove its correctness formally. The analyses of the other (simpler) filters follow with similar arguments.

Fig. 6

Filter6

Theorem 3

Filter6 solves problem P2 correctly.

Proof

Consider the pseudocode of Fig. 6. First, we need to show that matching M contains m − 2(m − k + 1) edges leading to dummy nodes $d_1, d_2, \ldots, d_{m-2(m-k+1)}.$ Let us call these dummy edges. For contradiction, assume that M has no dummy edge to some dummy node d _k′. We can obtain a matching M′ with smaller weight than M by replacing some positive weight edge, say e = (p _i , p _j ) ∈ M, with a dummy zero weight edge (p _′, d _k′), which gives the contradiction. (The degenerate case with w(M) = 0, i.e. with no positive weight edge, can be handled separately). Hence, m − 2(m − k + 1) pattern points are included in dummy edges, which leaves 2(m − k + 1) points to be matched to each others. These are the endpoints of the remaining (m − k + 1) edges in M. Let us call these split edges. We can now consider a splitting of the pattern into (m − k + 1) subsets each containing two pattern points from a distinct split edge, and the pattern points of dummy edges distributed to the subsets in an arbitrary way. Now, list L contains all real occurrence positions in the database, since all position are considered that match one of the split edges; a position that does not match any of the split edges can have no more than m − (m − k + 1) = k − 1 points in common with the pattern, and is no occurrence with the threshold k for the minimum size partial match. □

Filter6 is also optimal (produces least candidate positions) in the family of filters that examine m − k + 1 candidate lists.

3.3 Solving P2′

We consider the modified version of the partial match problem P2 where the user is allowed to mark points that have to be included in a match. Our solution assumes that at least one point is marked; if the user does not mark any, the first pattern point gets marked by default. When the reach constant α is used with the intra-database vectors, we use a suchlike constant β with the intra-pattern vectors in order to avoid the problem with losses. Constant β indicates how many points within the pattern can be jumped over by a intra-pattern vector. In this case, however, the jumps are allowed to go backwards, as well. That is, given a marked point j (1 ≤ j ≤ m), we need to consider intra-pattern vectors from $j-\beta-1,\ldots, j-1$ to j and from j to $j+1, \ldots, j+\beta+1$ (0 ≤ β ≤ min{m − j − 1, j − 2}).

For the filtering phase we now have two cases. In the first case the user has marked exactly one point (or we have the default instance) and the filter considers all intra-pattern vectors, possibly limited by the constant β, starting from it or ending to it. The occurrences of these vectors can be found obvious ways without or with an indexing structure. Finally, the found candidates are checked by executing PII.

In the second case we have at least two marked notes. The pattern is divided into two subpatterns P ^m and P ^r. Subpattern P ^m contains all the marked points while P ^r contains the remainder. In this case, P ^m is considered as the search pattern and for the filter we use Filter1. The checking phase becomes two-pronged. In the first subphase PI considers P ^m as the pattern and all candidate locations given by the filter need to be checked. The output of this phase consists of pairs (π, ϕ) where π gives the location of the occurrence and ϕ the used translation vector. Please note also that the output contains each and every of the true occurrences. What remains to be done, is to complete the found occurrences so that they become maximal. To this end, in the second checking phase, PII is executed at every found occurrence π checking whether the occurrence could be expanded with pattern P ^r using translation ϕ.

The filter phases are easy to analyse. In the first case we need to execute m searches in the index structure. Thus O(n) space and O(mlogn) time is needed for the filtration. In the second case O(logn) time suffices. The checking phase of the second case is interesting. Under any reasonable note distribution we may expect the first checking phase to fail, which means that at every candidate location PI will be executed but not PII. So, the expected running time for the checking phase is O(s), the worst case being O(smlogm), where s, s ≤ n, is the number of checked candidates.

In the experiments, these P2′ filters are called Filter7 and the filter variations are separable by the number of marked notes.

3.4 Summary

All the filters described above share in common the indexing phase; a subset of the intra-database vectors is stored in a binary search tree, each vector associated with their occurrence positions. Then, based on searching for a carefully selected subset of intra-pattern vectors from the binary search tree, each filter decides which are the candidate positions among the stored intra-database vectors that need to be further checked using an exact verification algorithm. The differences come in the way the candidates are selected and in the choice of the verification algorithm. The P2′ filtering algorithm (Filter7) uses a reduction to Filter1 and slightly modified checking phase, as described earlier. The properties of the different filters are summarized in Table 1.

Table 1 Properties of the different filters proposed

The parameters can be set into a partial order by analyzing how the filters work: $c_2\leq c_1 \leq i_2\leq i_3\leq i_4,$ c ₃ ≤ c ₀ (by expectation), c ₆ ≤ i ₄, and i ₅ ≤ i ₄.

4 Experiments

We set the new algorithms against the original Ukkonen et. al.’s PI and PII (Ukkonen et al. 2003). In the experiments the window length within the database (the reach constant α) was set to 50, the window length within the pattern in Filters 0–3, 6 to 5, and in Filters 4–5 to 12. In Filter6, we experimented with different values of k in range ${\lceil}\frac{1}{2}m{\rceil}$ to ${\lceil}{\frac{15}{16}}m{\rceil}.$ The selection of k has a great effect on the speed and accuracy of Filter6. Overall, these settings are a compromise between search time, index memory usage and search accuracy for difficult queries. Larger window lengths may be required for good accuracy depending on the level of polyphony and the type of expected queries.

We also compare with Clifford et. al.’s (2006) MsM ⁵ and Fredriksson and Grabowski’s (2008) Fg6 algorithm [Alg. 6.].⁶ The latter solves a slightly different problem; the time information is ignored (due to string representation of music, as discussed in Sect. 2), and the pitch values can differ by δ ≥ 0 after transposition. We set δ = 0 to make the setting as close to ours as possible. We also tested other algorithms in Fredriksson and Grabowski (2008) but Alg. 6 was constantly fastest among them in our setting.

To measure running times we experimented both on the length of the pattern and the database. Reported times are median values of more than 20 trials using randomly picked patterns. As substantial variations in the running times are characteristic to the filtering methods, we have depicted this phenomenon in one set of experiments by using box-whiskers: The whisker below a box represents the first quartile, while the second begins at the lower edge and ends at the median; the borders of third and fourth quartiles are given by the median, the upper edge of the box and the upper whisker, respectively.

We also wanted to measure how robust the PII-based methods (Filters 4–6) are against errors (effectively deletions) and noise (insertions), and calculated mean average precision and precision-against-recall plots in various settings. Here we reported the mean values of a 25-trial experiment in which the set of occurrences found by PII was considered as the ground truth. All the experiments were carried out with the MUTOPIA database;⁷ at the time it consisted of 1.9 million notes stored in 2270 MIDI files. All speed comparisons were run on a desktop PC with a 3 GHz Intel Pentium 4 HT processor and 1 GB of RAM. The C/C++ algorithm implementations were compiled with GCC 4.1, with most of the compiler optimizations enabled (-O3 -march = pentium4 etc.).

4.1 Experimenting on P1

First we experimented on the pattern size with the algorithms solving the P1 problem. The variations in the running times of the filters are depicted in Fig. 7a. Out of the four filters, Filter2 performed most stably while Filter0 had the greatest variation. The figure also shows that all our filtering methods constantly outperform both the original PI and the FG6 algorithm. With pattern sizes $|P| \,\lesssim\, 300,$ Filters 1 and 2 are the fastest ones, but with longer patterns Filter3 starts to dominate the results.

Fig. 7

Solving P1. Search time as function of pattern a (to the left) and database b (to the right) sizes. The database used for pattern experiments was the complete MUTOPIA collection with 1.9 million notes. Database size experiments were done with a pattern size of 64 notes. Note the logarithmic scales

The evident variation in our filters is caused by difficult patterns that only contain relatively frequently appearing indexed vectors. In our experiments, Filters 1–3 had search times of at most 2 ms. It is possible to generate patterns that have much longer search times, especially if the database is very monotonic or narrow windows are used. However, in practice these filters are at least 10 times faster than PI and 200 times faster than FG6 for every pattern of less than 1000 notes.

When experimenting on the size of the database as shown in Fig. 7b, execution times of online algorithms PI and FG6 increase linearly in the database size. Also Filter0’s search time increases at the same rate due to the poor filtering efficiency. Filters 1–3 have much lower slope because only few potential matches need to be verified after filtering (see Sect. 4.3 for more information on execution time allocation within Filter2). Figure 7b also depicts the construction time of the index structure for the filters. Remember that this costly operation needs to be executed only once for any database.

4.2 Experimenting on P2

Figure 8 shows the experimentally measured search times for the P2 filters, PII and MsM. When varying the size of the pattern, our PII-based filters clearly outperformed MsM in all practical cases (Fig. 8a): MsM becomes faster than PII only when |P| > 400 and faster than Filter4 when |P| > 1000. In this experiment Filter6 performs the best until $|P| \, > rsim \,250$ after which Filter5 starts to dominate. However, with a different setting of the parameters Filter6 can run faster, as the greedy version did in this experiment with $k={\frac{15}{16}}m.$

Fig. 8

Solving P2. Search time as function of pattern a (to the left) and database b (to the right) sizes. Database and pattern sizes as in Fig. 7

The results of the experiments on the length of the database are rather similar (Fig. 8b), exceptions being that MsM is constantly outperformed by the others and that Filter6 performs the best throughout the experiment. Again, a greedy version of Filter6 is the fastest: it is nearly 100 times faster than the basic Filter6 and over million times faster than MsM.

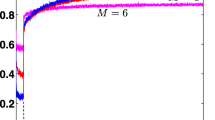
As Filter6 seems to perform the best on problem P2, we carried out a further experiment on the value of the parameter k. Figure 9 shows that the selection can affect the speed by two orders of magnitude. When searching for almost exact matches, using high values of k can shorten search times radically. Furthermore, greedy selection of pattern vectors seems to be more useful than searching for a perfect minimum-weight matching with high k values $(k={\frac{15}{16}}m)$ because searching for a graph matching starts to have an effect on the overall search time. On the other hand, better filtering efficiency of perfect matchings halves the search time at low k values $(k={\frac{1}{2}}m),$ compared to that of the greedy selection.

Fig. 9

Median search times of P2 Filter6 with different parameter values and varying pattern and database sizes. Database size in a was 1.9 million notes and pattern size in b was 64 notes

4.2.1 Comparing whole musical works

Clifford et al. (2006), carried out experiments for partial music matching and concluded that their algorithm is faster than PII when two whole documents are to be matched against each other. Figure 10 depicts results of our experiment using their setting but including also Filters 4–6. In our experiment, MsM becomes faster than PII when $|P|=|T| \, > rsim\, 600$ and dominates Filters 4 and 5 when the size of the matched documents exceeds 1000 and 5000 notes, respectively. Depending on the value of k, MsM becomes faster than Filter6 at document sizes larger than 1500–20,000 notes. However, in this specific task algorithms would be expected to return matches that are relatively poor if measured as a ratio between the matched notes and pattern size. Solving the task by using Filter6 with $k={\frac{15}{16}}$ would not give good results, but Filters 4, 5 and Filter6 with $k={\frac{1}{2}}m$ are comparable with MsM, as we will show below.

Fig. 10

Matching whole musical works against each other (|P| = |T|)

This experiment shows the foundational difference between P2-based algorithms and MsM: the first ones are to be used when dealing with musical pattern matching, MsM when comparing large musical works against each other.

4.2.2 Precision and recall

We wanted to experiment also on the robustness against pattern variations and noise. In the P2 problem, a change in onset or pitch of a note in the pattern or an occurrence will reduce the number of matched notes by one. The original PII algorithm finds all occurrences of a pattern where at least two notes match. However, our Filters 5–6 and MsM introduce lossy approximations and therefore some of the occurrences may be missed.

To measure the precision and recall of our filters against PII and MsM, we randomly picked 25 patterns from the database, created 25 variations of each and inserted the resulting 625 variations to random locations within the database. The specific pattern modifications were changed note onsets or pitches (errors) and inserted additional notes (noise). A change in note onset can be considered as a deletion with an accompanying insertion. PII is oblivious to insertions, but they reduce the accuracy of our filters when the insertion rate approaches the index reach constant α.

In each run, a maximum pattern error rate and noise level (number of added noise notes per each pattern note) was chosen and a list of occurrences was retrieved for all the 25 patterns with the original PII implementation. This ground truth was further trimmed by removing poor matches that exceeded the chosen maximum error rate. The same search was then executed with all the P2 filters and MsM, and their resulting occurrence lists were compared to the ground truth.

The resulting Precision–Recall curves at error rates 0.25, 0.5 and 0.75, with 16 added noise notes for each pattern note, can be seen in Fig. 11. For basic evaluation of the measurements, one can consider the area below a curve: the larger the area the better the accuracy and robustness of the corresponding algorithm. Filters 4–5 perform much better than MsM in all three tests, and with $k={\frac{1}{2}}m$ Filter6 is nearly lossless. By using higher values of k, Filter6 can be made much faster at the cost of accuracy, as the greedy version run with $k={\frac{15}{16}}m$ shows. Apparently MsM returns many false positives as its ordering of the results is inferior to that of the filters that verify the matches with a PII-based check.

Fig. 11

Precision–Recall graphs at database error rates 0.25, 0.5 and 0.75, with 16 noise notes added for each pattern note in the database

The most relevant information of the Precision–Recall graphs can be expressed in a tighter format by using Mean Average Precision (MAP) that represents the average precisions of a number of ranked queries. Figure 12a and b show the Mean Average Precision as a function of the maximum error rate at noise levels 0 and 20, respectively. These results reveal that MsM performs as well as Filters 5 and 6 at very high error rates, but again, it has problems ordering the results.

Fig. 12

Mean Average Precision of the P2 filters and on-line algorithms as compared to PII. a and b show MAP as a function of the ratio of changed notes in the database. In the second experiment (b), we also added 20 noise notes for each pattern note. In c MAP is a function of added noise notes

Noise level also affects the accuracy of our filters and MsM greatly, as can be seen in Fig. 12c. All filters are clearly constrained by the selected reach constant α = 50. Moreover, Filter6 is very vulnerable to noise at high values of k. The Mean Average Precision of MsM decreases more linearly and the algorithm overtakes Filters 5 and 6 when the noise level approaches α.

4.2.3 Experimenting on P2′

As the last search speed comparison, we measured how much a user may speedup the searching process with P2′-based algorithms by marking up notes that he/she is sure to be correct. P2 Filter6 was used as the point of comparison. Figure 13 depicts that when one note is marked, an indexing algorithm has a comparable performance to that of Filter6. When |P| > 300, pointing at least two notes makes the online algorithm more than 10 times faster than Filter6; the speedup with the P2′ index filters is at least thousandfold when more than one points are marked.

Fig. 13

Search times of P2′ online algorithm and filters (Filter7) compared to P2 Filter6. Database size in a was 1.9 million notes and pattern size in b was 64 notes. P2′ algorithm and filter variations are separated by the number of marked notes

4.3 Index filter execution time profiles

In addition to the comparisons between different algorithms, we measured time allocation profiles within two index filters: P1 Filter2 and P2 Filter6, with $k={\frac{1}{2}}m$ set for the latter. Results are shown in Fig. 14. This information can be used to improve the filtering algorithms and our implementations. For example, match verification dominates the execution time of Filter6 and therefore it could be improved by further optimizing the verification function or by retrieving less irrelevant matches in the actual filtering phase.

Fig. 14

Execution time profiles of P1 Filter2 (a, b) and P2 Filter6 (c, d) as function of pattern size (a, c, database size was 1.9 million notes) and database size (b, d, pattern size was 64 notes)

5 Conclusions

We considered three point pattern matching problems applicable to content-based music retrieval and showed how they can be solved using index-based filters. Given a point pattern P of m points, the problems are to find complete and partial matches of P within a database T of n points. The presented filters are lossless if O(n ²) space is available for indexing. We also introduced a more practical, linear size structure and sketched how the filters based on this structure become virtually lossless.

After the preprocessing of the database, the proposed filters f use O(g _f (m)logn + i _f ) time to produce c _f , c _f  ≤ i _f , candidate positions that are consequently checked for real occurrences with the existing online algorithms. The filters vary on the complexity of g _f (m), on the number of intermediate candidate positions i _f , and on the output size c _f . Since the filtering power of the proposed filters is hard to characterize theoretically, we ran several experiments to study the practical performance on typical inputs.

The experiments with the filters showed that they perform much faster than the existing online algorithms on typical content-based music retrieval scenarios. Only in the application of comparing large musical works in their entirety, the existing MsM algorithm (Clifford et al. 2006) is faster than our new filters.

A negative founding was that the proposed filters are not very stable; on all the filters the speed varies heavily depending on the properties of the pattern.

Since the guarantee of losslessness in the filters is only valid on limited search settings (number of mismatches allowed, constants limiting maximal reach, etc.), it was important to study also the precision and recall. This comparison was especially fruitful against MsM, that is an approximation algorithm, and can hence be considered as a lossy filter as well. The experiments showed that our filters typically outperform MsM in this respect.

As a future work, we plan to study the extensions of the filters to approximate point pattern matching; in addition to allowing partial matching, we could allow matching a point to some ε-distance from its target. Such setting gives a more robust way to model the query-by-humming application. Although it is straightforward to extend the filters to consider the candidate lists of all intra-database vectors within the given ε-threshold from any intra-pattern vector, the overall amount of candidate positions to check grows fast as the threshold is loosen. Therefore, finding better strategies for filtering in this scenario is an important future challenge.