A Unifying View on SMT-Based Software Verification

Abstract

After many years of successful development of new approaches for software verification, there is a need to consolidate the knowledge about the different abstract domains and algorithms. The goal of this paper is to provide a compact and accessible presentation of four SMT-based verification approaches in order to study them in theory and in practice. We present and compare the following different “schools of thought” of software verification: bounded model checking, k-induction, predicate abstraction, and lazy abstraction with interpolants. Those approaches are well-known and successful in software verification and have in common that they are based on SMT solving as the back-end technology. We reformulate all four approaches in the unifying theoretical framework of configurable program analysis and implement them in the verification framework CPAchecker. Based on this, we can present an evaluation that thoroughly compares the different approaches, where the core differences are expressed in configuration parameters and all other variables are kept constant (such as parser front end, SMT solver, used theory in SMT formulas). We evaluate the effectiveness and the efficiency of the approaches on a large set of verification tasks and discuss the conclusions.

1 Introduction

In recent years, advances in automatic methods for software verification have lead to an increased effort towards applying software verification to industrial systems, in particular operating-systems code [5, 8, 24, 56]. Predicate abstraction [47] with counterexample-guided abstraction refinement (CEGAR) [34] and lazy abstraction [51], lazy abstraction with interpolants [61], large-block encoding [11, 21], and k-induction with auxiliary invariants [13, 41] are some of the concepts that helped scale verification technology from simple example programs to real-world software. In the 6th International Competition on Software Verification (SV-COMP’17) [10], nine out of the 15 candidates participating in category Overall used some of these techniques, and out of the remaining six, four are bounded model checkers [26]. Considering this apparent success, we revisit an earlier work that presented a unifying algorithm for lazy predicate abstraction (Blast-like) and lazy abstraction with interpolants (Impact-like) and showed that both techniques perform similarly [25]. We extend this unifying framework to bounded model checking and k-induction  and conduct a comparative evaluation of bounded model checking, k-induction, lazy predicate abstraction, and lazy abstraction with interpolants. We observe that the previously drawn conclusions about the two lazy-abstraction techniques still hold today and show that even though abstraction is often necessary for scalability, k-induction has the potential to outperform the other two techniques. We restrict our presentation to safety properties; however, the techniques that we present can be used also for checking liveness [67].

Unfortunately, there is not much work available on rigorous comparison of algorithms. General overviews over methods for reasoning [9] and of approaches for software model checking [53] exist, but no systematic comparison of the algorithms in a common setting. This paper formulates four widely used SMT-based approaches for software verification in a common theoretical framework and tool implementation and compares their effectiveness and efficiency. Figure 1 tries to classify the approaches; in the following we use this structure also to give pointers to other implementations of the approaches.

Fig. 1

Classification of approaches

1.1 Bounded Model Checking

Many software bugs can be found by a bounded search through the state space of the program. Bounded model checking [26] for software encodes all program paths that result from a bounded unrolling of the program in an SMT formula that is satisfiable if the formula encodes a feasible program path from the program entry to a violation of the specification. Several implementations were demonstrated to be successful in improving software quality by revealing program bugs (especially on short paths), for example Cbmc [35], Esbmc [37], Llbmc [69], and Smack [64]. The characteristics to quickly verify even a large portion of the state space of many types of programs without the need of computing expensive abstractions made the technique a basis component in many verification tools (cf. Table 4 in the report for SV-COMP’17 [10]).

1.2 Unbounded without Abstraction¹

² The idea of bounded model checking (to encode portions of a program as SMT formula, even if they are large) can be used also for unbounded verification by using an induction argument [68], i.e., checking whether the safety property is implied by all paths from the program entry to the loop head and after assuming the safety property at the loop head (induction hypothesis) by all paths through the loop body. Because the safety property is often not inductive, the more general k-induction principle [70] is used. The approach of k-induction is implemented in Cbmc [35], CPAchecker [13], Esbmc [65], PKind [55], and 2ls [66]. The approach of strengthening k-induction proofs with continuously refining invariant generation [13] was independently reproduced later in 2ls [29].

1.3 Unbounded with Abstraction

A completely different approach is to compute an overapproximation of the state space, using insights from data-flow analysis [1, 57, 63]. While overapproximation can be a useful technique for mitigating the problem of state-space explosion, a too coarse level of abstraction may cause false alarms. Therefore, state-space abstraction is often combined with counterexample-guided abstraction refinement (CEGAR) [34] and lazy abstraction refinement [51]. Several verifiers implement a predicate abstraction [47]: for example, Slam [6], Blast [15], and CPAchecker [20]. A safe inductive invariant is computed by iteratively refining the abstract states, where new predicates are discovered during each CEGAR step. Interpolation [38, 60] is a successful method to obtain useful predicates from infeasible error paths; path invariants [17] can be used to obtain loop invariants for path programs.

Instead of using predicate abstraction, it is possible to construct the abstract state space directly from interpolants using the Impact algorithm [61].

1.4 Structure

In the remainder of this article, we first describe some necessary background in Sect. 2 and define a configurable program analysis as the foundation for unifying SMT-based approaches for software verification in Sect. 3. In Sect. 4, we express the four approaches within our framework and explain their core concepts and respective differences. Section 5 contains an experimental study of the effectiveness and efficiency of the presented approaches on a large set of verification tasks.

2 Background

2.1 Program Representation

In this section we provide basic definitions from the literature [15]. For simplicity, we restrict the presentation to a simple imperative programming language, where all operations are either assignments or assume operations, and all variables range over integers.³ Such a program can be represented using a control-flow automaton (CFA), which is a directed graph with program operations attached to its edges. A CFA ${A = ( L , { l _ INIT }, G)}$ consists of a set $L$ of program locations, an initial location ${ l _ INIT }\in L$ that represents the program entry point, and a set $G \subseteq ( L \times Ops\times L )$ of edges between program locations, each labeled with an operation that is executed when the control flows along the edge. The set of all program variables that occur in the operations of a CFA is denoted by $X$. A concrete data state $c: X\rightarrow \mathbb {Z}$ is a mapping from program variables to integers. A set of concrete data states is called region. We represent regions using first-order formulas $\psi$ over variables from X such that the set $[\![ \psi ]\!]$ of concrete data states that is represented by $\psi$ is defined as $\{c\mid c\models \psi \}$. A concrete state $(c, l): (X\rightarrow \mathbb {Z}) \times L$ is a pair of a concrete data state and a location.

An operation $op \in Ops$ can either be an assignment of the form $x := e$ with a variable $x\in X$ and a (side-effect free) arithmetic expression e over variables from X, or an assume operation [p] with a predicate p over variables from X. The semantics of an operation $op$ is defined by the strongest-postcondition operator ${\mathsf {SP}_{ op }({\cdot })}$. For a formula $\psi$ and an assignment $x:= e$, it is defined as ${\mathsf {SP}_{x:=e}({\psi })} = \exists \widehat{x}:\psi _{[x\rightarrow \widehat{x}]}\wedge (x = e_{[x\rightarrow \widehat{x}]})$, and for an assume operation [p] as ${\mathsf {SP}_{[p]}({\psi })} = \psi \wedge p$. Note that in the implementation we can avoid the existential quantifier in the strongest-postcondition operator for assignments by skolemization.

A path $\sigma = {\langle ( l _i, op _i, l _j),( l _j, op _j, l _k),\ldots ,( l _m, op _m, l _n) \rangle }$ is a sequence of consecutive edges from G. A path is called program path if it starts in the initial location ${ l _ INIT }$. The semantics of a path is defined by the iterative application of ${\mathsf {SP}_{ op }({\cdot })}$ for each operation of the path: ${\mathsf {SP}_{\sigma }({\psi })} = {\mathsf {SP}_{ op _m}({\ldots ({\mathsf {SP}_{ op _i}({\psi })})\ldots })}$. A path $\sigma$ is called feasible if ${\mathsf {SP}_{\sigma }({ true })}$ is satisfiable and infeasible otherwise. A location $l$ is called reachable if there exists a feasible path from ${ l _ INIT }$ to $l$.

A verification task consists of a CFA $A = ( L ,{ l _ INIT },G)$ and an error location ${{ l _ ERR }\in L }$, with the goal to show that ${ l _ ERR }$ is unreachable in A, or to find a feasible error path (i.e., a feasible program path to ${ l _ ERR }$) otherwise.

Fig. 2

An example C program (a) and its CFA (b)

2.2 Configurable Program Analysis

A configurable program analysis (CPA) [18] specifies the abstract domain that is used for a program analysis. By using the concept of CPAs we can define the abstract domain independently from the analysis algorithm: the CPA algorithm is an algorithm for reachability analysis that can be used with any CPA. Furthermore, CPAs can be combined to compositions of CPAs. The CPAs defined in this work make use of the extension CPA+ (dynamic precision adjustment) [19], but for simplicity we continue to name them CPAs.

A CPA $\mathbb {D}= (D, {\varPi }, \rightsquigarrow , \mathsf {merge}, \mathsf {stop}, \mathsf {prec})$ consists of an abstract domain D, a set ${\varPi }$ of precisions, a transfer relation $\rightsquigarrow$, and the operators $\mathsf {merge}$, $\mathsf {stop}$, and $\mathsf {prec}$. The abstract domain $D = (C, \mathcal {E}, [\![ \cdot ]\!])$ consists of a set C of concrete states, a semilattice $\mathcal {E}= (E, \sqsubseteq )$ over a set $E$ of abstract-domain elements (i.e., abstract states) and a partial order $\sqsubseteq$ (the join $\sqcup$ of two elements and the join $\top$ of all elements are unique), and a concretization function $[\![ \cdot ]\!]$ that maps each abstract-domain element to the represented set of concrete states. We call an abstract state $e\in E$ an abstract error state if it represents a concrete state at the error location ${ l _ ERR }$, i.e., if $\exists c \in (X\rightarrow \mathbb {Z}): (c,{ l _ ERR }) \in [\![ e ]\!]$. The transfer relation $\rightsquigarrow \subseteq E\times E\times {\varPi }$ computes abstract successor states under a precision. The merge operator $\mathsf {merge}: E\times E\times {\varPi }\rightarrow E$ specifies if and how to merge two abstract states when control flow meets under a given precision. The stop operator $\mathsf {stop}: E\times 2^E\times {\varPi }\rightarrow \mathbb {B}$ determines whether an abstract state is covered by a given set of abstract states. The precision-adjustment operator $\mathsf {prec}: E\times {\varPi }\times 2^{E\times {\varPi }} \rightarrow E\times {\varPi }$ allows adjusting the analysis precision dynamically depending on the current set of reachable abstract states. The operators $\mathsf {merge}$, $\mathsf {stop}$, and $\mathsf {prec}$ can be chosen appropriately to influence the abstraction level of the analysis. Common choices include $\mathsf {merge}^ sep (e,e',\pi ) = e'$ (which does not merge abstract states), $\mathsf {stop}^ sep (e,R,\pi ) = (\exists e' \in R: e \sqsubseteq e')$ (which determines coverage by checking whether the given abstract state is less than or equal to any other reachable abstract state according to the semilattice), and $\mathsf {prec}^{id}(e,\pi ,\cdot ) = (e,\pi )$ (which keeps abstract state and precision unchanged).

2.2.1 CPA Algorithm

CPAs can be used by the CPA algorithm for reachability analysis (cf. Algorithm 1), which gets as input a CPA and an initial abstract state with precision. The algorithm does a classic fixed-point iteration by looping until the set $\mathsf {waitlist}$ is empty (all abstract states have been completely processed) and returns the set of reachable abstract states. In each iteration, the algorithm takes one abstract state $e$ with precision $\pi$ from the waitlist, passes them to the precision-adjustment operator $\mathsf {prec}$, computes all abstract successors, and processes each of the successors. The algorithm checks if there is an existing abstract state with precision in the set of reached states with which the successor abstract state is to be merged (e.g., at join points where control flow meets after completed branching). If this is the case, then the new, merged abstract state with precision substitutes the existing abstract state with precision in both sets $\mathsf {reached}$ and $\mathsf {waitlist}$. The stop operator ensures that a new abstract state is inserted into the work sets only if this is needed, i.e., the abstract state is not already covered by an abstract state in the set $\mathsf {reached}$.

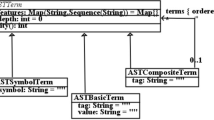
2.2.2 Composite CPA

Several CPAs can be combined (Composite pattern) using a Composite CPA [18]. The abstract states of the Composite CPA are tuples of one abstract state from each component CPA, the precisions of the Composite CPA are tuples of one precision from each component CPA, and the operators of the Composite CPA delegate to the component CPAs’ operators accordingly.

The effect of such a combination of CPAs is that all used CPAs work together in eliminating infeasible paths during the program analysis: one CPA might be able to prove some specific paths infeasible, whereas other CPAs might rule out other infeasible paths. The analysis will only find paths which all used CPAs agree to be feasible. Note that this effect already occurs without any form of communication or information exchange between the component CPAs, and neither does any of the component CPAs need to know anything about the others. However, for an even higher precision, information exchange is possible if desired using the strengthen operator $\mathord {\downarrow }$ [18] and precision-adjustment operator $\mathsf {prec}$ [19] of the Composite CPA.

2.2.3 Basic CPAs

The possibility to combine CPAs by using a Composite CPA allows us to separate different concerns: we extract certain common analysis components into separate CPAs and reuse them in flexible combinations with other CPAs, instead of having to redefine them for every analysis from scratch.

For example, for most kinds of program analyses it is necessary to track the program counter, and it is often efficient to track the program counter explicitly rather than symbolically. Thus, we use the Location CPA $\mathbb {L}$ [19], which tracks exactly the program counter (with a flat lattice over all program locations, a constant precision, and the operators $\mathsf {merge}^ sep$, $\mathsf {stop}^ sep$, and $\mathsf {prec}^{id}$), and we use this CPA in addition to other CPAs whenever explicit tracking of the program counter is necessary.

Furthermore, in order to track the abstract reachability graph (ARG) over the abstract states in the (flat) set $\mathsf {reached}$, we define an additional ARG CPA $\mathbb {A}$, which stores the predecessor–successor relationship between abstract states. The ARG CPA allows us to reconstruct abstract paths in the ARG: An abstract path is a sequence ${\langle e_0,\ldots ,e_n \rangle }$ of abstract states such that for any pair $(e_i,e_{i+1})$ with $i\in \{0, \ldots , n-1\}$ either $e_{i+1}$ is an abstract successor of $e_{i}$, or $e_{i+1}$ is the result of merging an abstract successor of $e_{i}$ with some other abstract state(s). If both the Location CPA and the ARG CPA are used, we can reconstruct from an abstract path the path that it represents in the CFA.

2.3 Counterexample-Guided Abstraction Refinement (CEGAR)

Counterexample-guided abstraction refinement (CEGAR) [34] is an approach for iteratively finding an analysis precision that is strong enough to prove the program safe and coarse enough to allow for an efficient analysis. Starting with a coarse initial precision (typically an empty set of facts, e.g., predicates), an abstract model that is an overapproximation of the program is created by the underlying reachability analysis. If an abstract state that belongs to the error location is found in the abstract model, the concrete program path that leads to this state is reconstructed from the ARG and checked for feasibility. If the error path is feasible, the program is unsafe and the analysis terminates. Otherwise, the error path is infeasible, and we refine the precision of the analysis to be precise enough to eliminate this infeasible error path from the ARG. Then the analysis is restarted, and the steps are repeated until either a concrete error path is found, or the abstract model (and thus the program) is proven safe.

CEGAR is often combined with lazy abstraction [51], which makes this approach more efficient by increasing the precision only selectively in parts of the state space where it is needed and by not restarting the analysis from scratch after each refinement. We use the CPA algorithm for the creation of the abstract model in the CEGAR approach and let the refinement influence the precision of the used CPA(s).

3 Predicate CPA

Our goal is to define a configurable and flexible framework for predicate-based approaches that is helpful both in theory (by simplifying development and studying of approaches) as well as in practice (by being customizable for different use cases). In addition, a mature and efficient implementation of this framework should allow reliable scientific experiments and application in practice of the approaches that are integrated now or in the future.

The core of our framework is defined as a CPA for predicate-based analyses, which we name the Predicate CPA $\mathbb {P}$. It is an extension of an existing CPA for predicate abstraction with adjustable-block encoding (ABE) [21], and a preliminary version was already published [25]. The Predicate CPA $\mathbb {P}= (D_\mathbb {P}, {\varPi }_\mathbb {P}, \rightsquigarrow _\mathbb {P}, \mathsf {merge}_\mathbb {P}, \mathsf {stop}_\mathbb {P}, \mathsf {prec}_\mathbb {P})$ consists of the abstract domain $D_\mathbb {P}$, the set ${\varPi }_\mathbb {P}$ of precisions, the transfer relation $\rightsquigarrow _\mathbb {P}$, the merge operator $\mathsf {merge}_\mathbb {P}$, the stop operator $\mathsf {stop}_\mathbb {P}$, and the operator $\mathsf {prec}_\mathbb {P}$ for dynamic precision adjustment. Additionally, we will define an operator $\mathsf {fcover}_\mathbb {P}$ for Impact-style forced covering and an operator $\mathsf {refine}_\mathbb {P}$ for refinements. In the following, we will define and describe these parts in more details. We also provide an extended version of the CPA algorithm, and in the next section we will describe how to express various algorithms for software verification using the concepts defined here. The examples in this section illustrate some cases that occur when verifying the running example program given in Fig. 2 using one of these algorithms from Sect. 4.

3.1 Abstract Domain, Precisions, and CPA Operators

The abstract domain $D_\mathbb {P}= (C, \mathcal {E}_\mathbb {P}, [\![ \cdot ]\!]_\mathbb {P})$ consists of the set C of concrete states, the semilattice $\mathcal {E}_\mathbb {P}$ over abstract states, and the concretization function $[\![ \cdot ]\!]_\mathbb {P}$. The semilattice $\mathcal {E}_\mathbb {P}= (E_\mathbb {P}, \sqsubseteq _\mathbb {P})$ consists of the set $E_\mathbb {P}$ of abstract states and the partial order $\sqsubseteq _\mathbb {P}$.

3.1.1 Abstract States

Because of the use of adjustable-block encoding [21], an abstract state $e\in E_\mathbb {P}$ of the Predicate CPA is a triple $(\psi ,{{l^\psi }^{}_{\!\!}},\varphi )$ of an abstraction formula $\psi$, the abstraction location ${{l^\psi }^{}_{\!\!}}$ (the program location where $\psi$ was computed), and a path formula $\varphi$. Both formulas are first-order formulas over predicates over the program variables from the set $X$, and an abstract state represents all concrete states that satisfy their conjunction: $[\![ (\psi ,{{l^\psi }^{}_{\!\!}},\varphi ) ]\!]_\mathbb {P}= \{(c,\,\cdot ) \in C\mid c \models (\psi \wedge \varphi )\}$. The partial order $\sqsubseteq _\mathbb {P}$ is defined as $(\psi _1,{{l^\psi }^{}_{\!\!1}},\varphi _1) \sqsubseteq _\mathbb {P}(\psi _2,{{l^\psi }^{}_{\!\!2}},\varphi _2) = \left( (\psi _1\wedge \varphi _1) \Rightarrow (\psi _2\wedge \varphi _2)\right)$, i.e., an abstract state is less than or equal to another state if the conjunction of the formulas of the first state implies the conjunction of the formulas of the other state. Abstract states where the path formula $\varphi$ is $true$ are called abstraction states, other abstract states are intermediate states. The transfer relation produces only intermediate states, and at the end of a block of program operations the operator $\mathsf {prec}$ computes an abstraction state from an intermediate state. The initial abstract state is the abstraction state $( true , l _ INIT , true )$.

The path formula of an abstract state is always represented syntactically as an SMT formula. The representation of the abstraction formula, however, can be configured. We can either use a binary-decision diagram (BDD) [31], as in classic predicate abstraction [15, 47], or an SMT formula similar to the path formula. Using BDDs allows performing cheap entailment checks between abstraction states at the cost of an increased effort for constructing the BDDs.

3.1.2 Precisions

A precision $\pi \in {\varPi }_\mathbb {P}$ of the Predicate CPA is a mapping from program locations to sets of predicates over the program variables. This allows using a different abstraction level at each location in the program (lazy abstraction). The initial precision is typically the mapping $\pi ( l ) = \emptyset$, for all $l \in L$. The Predicate CPA does not use dynamic precision adjustment [19] during an execution of the CPA algorithm: instead the precision is adjusted only during a refinement step, if the predicate refinement strategy is used. The only operation that changes its behavior based on the precision is the predicate abstraction that may be computed at block ends by the operator $\mathsf {prec}_\mathbb {P}$.

3.1.3 Transfer Relation

The transfer relation $(\psi ,{{l^\psi }^{}_{\!\!}},\varphi ) \rightsquigarrow ((\psi ,{{l^\psi }^{}_{\!\!}},\varphi '),\pi )$ for a CFA edge $(l_i, op _i, l_j)$ produces a successor state $(\psi ,{{l^\psi }^{}_{\!\!}},\varphi ')$ such that the abstraction formula and location stay unchanged and the path formula $\varphi '$ is created by applying the strongest-postcondition operator for the current CFA edge to the previous path formula: $\varphi ' = {\mathsf {SP}_{ op _i}({\varphi })}$. Note that this is an inexpensive, purely syntactical operation that does not involve any actual solving, and that it is a precise operation, i.e., it does not perform any form of abstraction.

3.1.4 Merge Operator

The merge operator $\mathsf {merge}_\mathbb {P}$ combines intermediate states that belong to the same block (their abstraction formula and location is the same) and keeps any other abstract states separate:

$$\begin{aligned}&\mathsf {merge}_\mathbb {P}\left( \left( \psi _1,{{l^\psi }^{}_{\!\!1}},\varphi _1\right) , \left( \psi _2,{{l^\psi }^{}_{\!\!2}},\varphi _2\right) , \pi \right) \\&\quad {=} {\left\{ \begin{array}{ll} \left( \psi _2, {{l^\psi }^{}_{\!\!2}}, \varphi _1 \vee \varphi _2\right) &{} \text {if}\quad (\psi _1 = \psi _2) \wedge \left( {{l^\psi }^{}_{\!\!1}} = {{l^\psi }^{}_{\!\!2}}\right) \\ \left( \psi _2,{{l^\psi }^{}_{\!\!2}},\varphi _2\right) &{} \text {otherwise} \end{array}\right. } \end{aligned}$$

This definition is common for analyses based on adjustable-block encoding (ABE) [21]. By merging abstract states inside each block, the number of abstract states in the ARG is kept small, and no precision is lost due to merging, because the path formula of an abstract state exactly represents the path(s) from the block start without abstraction. At the same time the loss of information that would lead to a path-insensitive analysis if states would be merged across blocks is avoided. The result is that the ARG, if projected to contain only abstraction states, forms an abstract-reachability tree (ART) like in a path-sensitive analysis without ABE. This is necessary for being able to reconstruct abstract paths, for example during refinement and for reporting concrete error paths.

3.1.5 Stop Operator

The stop operator $\mathsf {stop}_\mathbb {P}$ checks coverage only for abstraction states and always returns $false$ for intermediate states:

$$\begin{aligned}&\mathsf {stop}_\mathbb {P}((\psi ,{{l^\psi }^{}_{\!\!}},\varphi ), R, \pi ) \\&\quad {=} {\left\{ \begin{array}{ll} \exists (\psi ',{{l^\psi }^{}_{\!\!}}',\varphi ') \in R: \varphi '= true \wedge (\psi ,{{l^\psi }^{}_{\!\!}},\varphi ) \sqsubseteq _\mathbb {P}(\psi ',{{l^\psi }^{}_{\!\!}}',\varphi ') &{}\text {if}\quad \varphi = true \\ false &{} \text {otherwise} \end{array}\right. } \end{aligned}$$

Because the path formula of an abstraction state is always $true$, the first case is equivalent to checking if there exists an abstraction state $(\psi ',\cdot , true )$ in the set R whose abstraction formula $\psi '$ is implied by the abstraction formula $\psi$ of the current abstraction state $(\psi , {{l^\psi }^{}_{\!\!}}, \varphi )$. If abstraction formulas are represented by BDDs, this is an efficient operation, otherwise a potentially costly SMT query is required. The coverage check for intermediate states is omitted for efficiency, because it would always need to involve (potentially many) SMT queries. Note that this implies that infinitely long sequences of intermediate states must be avoided, otherwise the analysis would not terminate.

3.1.6 Precision-Adjustment Operator

The precision-adjustment operator $\mathsf {prec}_\mathbb {P}$ either returns the input abstract state and precision, or converts an intermediate state into an abstraction state performing predicate abstraction. The decision is made by the block-adjustment operator $\mathsf {blk}$ [21], which returns $true$ or $false$ depending on whether the current block ends at the current abstract state and thus an abstraction should be computed. The decision can be based on the current abstract state as well as on information about the current program location. We define the following common choices for $\mathsf {blk}$: $\mathsf {blk}^{{ lf}}$ returns $true$ at loop heads, function calls/returns, and at the error location ${ l _ ERR }$, leading to a behavior similar to large-block encoding (LBE) [11]. $\mathsf {blk}^{l}$ returns $true$ only at loop heads and at the error location ${ l _ ERR }$. The abstraction at the error location is needed for detecting the reachability of abstract error states due to the satisfiability check that is implicitly done by the abstraction computation if the precision is not empty. $\mathsf {blk}^ never$ always returns $false$. This will prevent all abstractions and (due to how $\mathsf {stop}_\mathbb {P}$ is defined) also prevents coverage between abstract states. This means that an analysis with $\mathsf {blk}^ never$ will unroll the CFA endlessly until other reasons prevent this. We will show a meaningful application of $\mathsf {blk}^ never$ in Sect. 4.1 (BMC).

The boolean predicate abstraction [7] $({\varphi })^{\rho }_{\mathbb {B}}$ of a formula $\varphi$ for a set $\rho$ of predicates is the strongest boolean combination of predicates from $\rho$ that is implied by $\varphi$. It can be computed using an SMT solver by solving $\varphi \wedge \bigwedge _{p_i\in \rho } (v_{p_i} \Leftrightarrow p_i)$ and enumerating all its models with respect to the fresh boolean variables $v_{p_1},\ldots ,v_{p_{|\rho |}}$. For each model we create a conjunction over the predicates from $\rho$, with each predicate $p_i$ being negated if the model maps the corresponding variable $v_{p_i}$ to $false$. The result of $({\varphi })^{\rho }_{\mathbb {B}}$ is the disjunction of all these conjunctions. To create an abstraction state from an intermediate state $(\psi ,{{l^\psi }^{}_{\!\!}},\varphi )$ at program location $l$ (which is tracked by another CPA that runs in parallel to the Predicate CPA as a sibling component within the same Composite CPA and from which the location can be retrieved), we compute the boolean predicate abstraction $({\psi \wedge \varphi })^{\pi ( l )}_{\mathbb {B}}$ for the formula $\psi \wedge \varphi$ and the set $\pi ( l )$ of predicates from the precision, after adjusting the variable names of $\psi$ to match those of $\varphi$ (because the variables from $\psi$ need to match the ’oldest’ variables in $\varphi$). Thus, we can define the precision-adjustment operator as

$$\begin{aligned} \mathsf {prec}_\mathbb {P}\left( \left( \psi ,{{l^\psi }^{}_{\!\!}},\varphi \right) ,\pi ,R\right) = {\left\{ \begin{array}{ll} \left( \left( ({\psi \wedge \varphi })^{\pi ( l )}_{\mathbb {B}}, l , true \right) , \pi \right) &{} \text {if}\quad \mathsf {blk}\left( \left( \psi ,{{l^\psi }^{}_{\!\!}},\varphi \right) , l\right) \\ \left( \left( \psi ,{{l^\psi }^{}_{\!\!}},\varphi \right) , \pi \right) &{}\text {otherwise } \end{array}\right. } \end{aligned}$$

Note that, if an abstraction is going to be computed, the current path formula $\varphi$ precisely represents all the paths within this block (i.e., from the last abstraction state to the current abstract state). Thus, we name this path formula the block formula for the block ending in the current abstract state. If the precision is empty for the current program location, the outcome of the abstraction computation will always simply be $true$ and no SMT queries are necessary. If the precision for the current program location is $\{ false \}$, the abstraction computation will be equivalent to a simple satisfiability check, and the outcome will always be either $true$ or $false$.

3.2 Refinement

The refinement operator $\mathsf {refine}_\mathbb {P}$ takes as input two sets $\mathsf {reached}\subseteq E\times {\varPi }$ of reached abstract states and $\mathsf {waitlist}\subseteq E\times {\varPi }$ of frontier abstract states and expects $\mathsf {reached}$ to contain an abstract error state at error location ${ l _ ERR }$ that represents a specification violation. $\mathsf {refine}$ either returns the sets unchanged (if the abstract error state is reachable, i.e., there is a feasible error path), or modified such that the sets can be used for continuing the state-space exploration with an increased precision (if the error path is infeasible). The operator works in four steps.

3.2.1 Abstract-Counterexample Construction

The first step is to construct the set of abstract paths between the initial abstract state and the abstract error state. Traditionally, in an abstract reachability tree, there would exist exactly one such abstract path. Because we use ABE, however, intermediate states can be merged, and thus the abstract states form an abstract reachability graph, where several paths can exist from the initial abstract state to the abstract error state. All these abstract paths to the abstract error state contain the same sequence of abstraction states with varying sequences of intermediate states in between. This is due to the fact that abstraction states are never merged, and intermediate states are merged only locally within a block. Thus, the ARG, if projected to the abstraction states, still forms a tree. The initial abstract state is always an abstraction state by definition, and our choices of the block-adjustment operator $\mathsf {blk}$ ensure that all abstract error states are also abstraction states. Thus, we define as abstract counterexample the sequence ${\langle e_0,\ldots ,e_n \rangle }$ that begins with the initial abstract state ($e_0 = e_ INIT$), ends with the abstract error state $e_n$, and contains all abstraction states $e_1,\ldots ,e_{n-1}$ on paths between these two abstract states. This sequence can be reconstructed from the ARG by following a single arbitrary abstract path backwards from the abstract error state (using the information tracked by the ARG CPA), without needing to explicitly enumerate all (potentially exponentially many) abstract paths between the initial abstract state and the abstract error state.

3.2.2 Feasibility Check

From an abstract counterexample ${\langle e_0,\ldots ,e_n \rangle }$ we can create a sequence ${\langle \varphi _1,\ldots ,\varphi _n \rangle }$ of block formulas where each $\varphi _i$ represents all paths between $e_{i-1}$ and $e_i$. Note that each $\varphi _i$ is also exactly the same formula as the path formula that was used as input when computing the abstraction for state $e_i$. Then we check whether there exists a feasible concrete path that is represented by one of the abstract paths of the abstract counterexample by checking the counterexample formula $\bigwedge _{i=1}^n \varphi _i$ for satisfiability in a single SMT query. If satisfiable, the analysis has found a violation of the specification and terminates. Otherwise, i.e., if all abstract paths to the abstract error state are infeasible under the concrete program semantics, we say that the abstract counterexample is spurious, and a refinement of the abstract model is necessary to eliminate this infeasible error path from the ARG.

3.2.3 Interpolation

To refine the abstract model, $\mathsf {refine}_\mathbb {P}$ uses Craig interpolation [38] to discover abstract facts that allow eliminating the infeasible error path. Given a sequence ${\widehat{\varphi }={\langle \varphi _1,\ldots ,\varphi _n \rangle }}$ of formulas whose conjunction is unsatisfiable, a sequence ${\langle \tau _0,\ldots ,\tau _n \rangle }$ is an inductive sequence of interpolants for $\widehat{\varphi }$ if

• 1. $\tau _0 = true$ and $\tau _n = false$,

• 2. $\forall i\in \{1,\ldots ,n\} : \tau _{i-1}\wedge \varphi _i \Rightarrow \tau _i$, and

• 3. for all $i\in \{1,\ldots ,n-1\}$, $\tau _i$ references only variables that occur in $\bigwedge _{j=1}^i \varphi _i$ as well as in $\bigwedge _{j=i+1}^n \varphi _i$.

Note that every interpolation sequence starts with no assumption ($\tau _0 = true$) and ends with a contradiction ($\tau _n = false$), and that $\tau _i\Rightarrow \lnot \bigwedge _{j=i+1}^n \varphi _j$ follows from the definition, for all $i\in \{1,\ldots ,n\}$. For many common SMT theories, interpolants are guaranteed to exist and can be computed using off-the-shelf SMT solvers from a proof of unsatisfiability for $\bigwedge _{i=1}^n \varphi _i$. Note that in general there exist many possible sequences of interpolants for a single infeasible error path.

3.2.4 Refinement Strategies

Lastly, $\mathsf {refine}_\mathbb {P}$ needs to refine the precision of the analysis such that afterwards the analysis is guaranteed to not encounter the same error path again. A refinement strategy uses the current spurious abstract counterexample ${\langle e_0,\ldots ,e_n \rangle }$ and the corresponding sequence ${\langle \tau _0,\ldots ,\tau _n \rangle }$ of interpolants to modify the sets $\mathsf {reached}$ and $\mathsf {waitlist}$. For this step, two common approaches exist. Afterwards, the refinement is finished, the modified sets $\mathsf {reached}$ and $\mathsf {waitlist}$ are returned to the analysis, and the analysis continues with building the abstract model (which will now be more precise).

Fig. 3

Sketches of the process of rechecking coverage relations after Impact refinement. Squiggly arrows represent paths between abstraction states and hide intermediate states

Impact Refinement.  One refinement strategy is to perform a refinement similar to the function Refine of the Impact algorithm [61]. The Impact refinement strategy takes each abstraction state $\psi _i$ of the abstract counterexample and conjoins to its abstraction formula the corresponding interpolant $\tau _i$. If an abstract state is actually strengthened by this (i.e., the previous abstraction formula did not already imply the interpolant), we also need to recheck all coverage relations of this abstract state. Figure 3a outlines such a situation: an abstract state $e_i'$ previously covered by another abstract state $e_i$ is now no longer covered, because the abstraction formula of $e_i$ was strengthened by the refinement. In this case, we uncover and readd all leaf abstract states in the subgraph of the ARG that starts with the uncovered abstract state $e_i'$ to the set $\mathsf {waitlist}$. We also check for each of the strengthened abstract states whether it is now covered by any other abstract state at the same program location. If this is successful, i.e., if a strengthened abstract state $e_j$ is now covered by another abstract state $e_j'$ as shown in Fig. 3b, we mark the subgraph that starts with that strengthened abstract state $e_j$ as covered and remove all leafs therein from $\mathsf {waitlist}$ (we do not need to expand covered abstract states). The only change to the set $\mathsf {reached}$ is the removal of all abstract states whose abstraction formula is now equivalent to $false$ and their successors. Due to the properties of interpolants, this is guaranteed to be the case for at least the abstract error state.

Predicate Refinement. Another refinement strategy is used for traditional lazy predicate abstraction. It extracts the atoms of the interpolants as predicates, creates a new precision $\pi$ with these predicates, and restarts (a part of) the analysis with a new precision that is extended by $\pi$.

The precision $\pi$ is a mapping from program locations to sets of predicates, and we add predicates to the precision only for program locations where they are necessary. Assuming that, starting from an abstract counterexample ${\langle e_0,\ldots ,e_n \rangle }$ with abstraction states at program locations ${\langle l _0,\ldots , l _n \rangle }$ we obtained a sequence ${\langle \tau _0,\ldots ,\tau _n \rangle }$ of interpolants and extracted a sequence ${\langle \rho _0,\ldots ,\rho _n \rangle }$ of sets of predicates. Then we add each predicate to the precision for the program location that corresponds to the point in the abstract counterexample where the predicate appears in the interpolant, i.e., $\pi ( l ) = \bigcup _{i=0}^n (\rho _i\text { if } l = l _i\text { else }\emptyset )$. Note that due to the properties of interpolants, $\pi ({ l _ ERR })$ will always be $\{ false \}$. We take the precision $\pi$ with the new predicates and the existing precision $\pi _n$ that is associated in the set $\mathsf {reached}$ with the abstract error state $e_n$ and join them element-wise to create the new precision $\pi '$ with $\forall l \in L : \pi '( l ) = \pi _n( l ) \cup \pi ( l )$ that will be used in the subsequent analysis.

Finally, the sets $\mathsf {reached}$ and $\mathsf {waitlist}$ are prepared for continuing with the analysis. We remove only those parts of the ARG for which the new predicates are necessary. For this, we determine the first abstract state of the abstract counterexample for which the new precision $\pi '$ would lead to more predicates being used in the abstraction computation than the originally used predicates and call this the pivot abstract state. Then we remove the subgraph of the ARG that starts with the pivot abstract state from the sets $\mathsf {reached}$ and $\mathsf {waitlist}$, as well as all abstract states that were covered by one of the removed abstract states. To ensure that the removed parts of the ARG get re-explored, we take all remaining parents of removed abstract states, replace the precision with which they are associated in $\mathsf {reached}$ with the new precision $\pi '$, and add them to the set $\mathsf {waitlist}$. This has not only the effect of avoiding the re-exploration of unchanged parts of the ARG, but also leads to the new predicates being used only in the relevant part of the ARG, with other parts of the program state space being explored with different (possibly more abstract and thus more efficient) precisions.

3.3 Forced Covering

Forced coverings were introduced for lazy abstraction with interpolants (Impact) [61] for a faster convergence of the analysis. Typically, when the CPA algorithm creates a new successor abstract state for an Impact analysis, this new abstract state is too abstract to be covered by existing abstract states, since the Impact refinement strategy is used, which leads to all new abstraction states being equivalent to $true$. If an abstract state cannot be covered, the analysis needs to further create successors of it, leading to more abstract states and possibly more refinements. The idea of forced covering is to strengthen new abstract states such that they are covered by existing abstract states immediately if possible.

We define an operator $\mathsf {fcover}_\mathbb {P}: 2^{E\times {\varPi }} \times E\times {\varPi }\rightarrow 2^{E\times {\varPi }}$ that takes as input the set $\mathsf {reached}$ of reachable abstract states and an abstract state $e$ with precision $\pi$ and returns an updated set $\mathsf {reached}'$ of reachable abstract states. The operator may replace $e$ and other abstract states in $\mathsf {reached}$ with strengthened versions, if it can guarantee that this is sound and if afterwards the strengthened version of $e$ is covered by another abstract state in $\mathsf {reached}'$. A trivial implementation of this operator is $\mathsf {fcover}^ id (\mathsf {reached}, e, \pi ) = \mathsf {reached}$, which does not strengthen abstract states and returns the set $\mathsf {reached}$ unchanged.

An alternative implementation is $\mathsf {fcover}^{\textsc {Impact}}$, which adopts the strategy for forced coverings presented for lazy abstraction with interpolants [61]. We extend this approach here to support adjustable-block encoding. Because the Predicate CPA does not attempt to cover intermediate states (only abstraction states), we also only attempt forced coverings for abstraction states. Figure 4 shows a sketch of the concept of forced covering in Impact to help visualize the following explanation: Given an abstraction state $e$ that should be covered if possible, the candidate abstract states for covering are those abstraction states that belong to the same location, were created before $e$, and are not covered themselves. For each candidate $e'$, we first determine the nearest common ancestor abstraction state $\hat{e}$ of $e$ and $e'$ (using the information tracked by the ARG CPA). Now let us denote the abstraction formulas of $e'$ and $\hat{e}$ with $\psi '$ and $\hat{\psi }$, respectively, and let $\varphi$ be the path formula that represents the paths from $\hat{e}$ to $e$. We then determine whether $\psi '$ also holds for $e$ by checking if $\hat{\psi } \wedge \varphi \implies \psi '$ holds, i.e., whether it is impossible to reach a concrete state that is not represented by $\psi '$ when starting at $\hat{e}$ and following the paths to $e$. If this holds, we can strengthen the abstraction formula of $e$ with $\psi '$ (which immediately lets us cover $e$ by $e'$). Furthermore, if there are abstraction states along the paths from $\hat{e}$ to $e$, we need to strengthen these states, too, in order to keep the ARG well-formed. We can do so by computing interpolants at the appropriate locations along the paths for the query that we have just solved and strengthen the abstract states with the interpolants. If the query does not hold, we switch to the next candidate abstract state and try again. Finally, $\mathsf {fcover}^{\textsc {Impact}}$ returns an updated set $\mathsf {reached}$ with strengthened abstract states, or the original set $\mathsf {reached}$ if forced covering was unsuccessful for each of the candidates. Note that this forced-covering strategy is similar to interpolation-based refinement with the Impact refinement strategy, just that we attempt to prove that $\psi '$ instead of $false$ holds at the end of the path, and that the refined path does not start at the initial abstract state but at $\hat{e}$.

Fig. 4

Concept sketch for  $\mathsf {fcover}^{\textsc {Impact}}$, blue parts are added on successful forced covering, i.e.,  if $\hat{\psi }\wedge \varphi \Rightarrow \psi '$

3.4 An Extended CPA Algorithm

In order to be able to use all the features of the Predicate CPA and support approaches such as lazy abstraction, we also need to slightly extend the CPA algorithm. The extended version, which we call the CPA++ algorithm, is shown as Algorithm 2. Compared to the original version (Algorithm 1), it has the following differences:

• 1. CPA++ gets $\mathsf {reached}$ and $\mathsf {waitlist}$ as input and returns updated versions of both of them, instead of getting an initial abstract state and returning a set of reachable abstract states.

• 2. CPA++ calls a function $\mathsf {abort}$ to determine whether it should abort early for each found abstract state (lines 16–17).

• 3. CPA++ calls the precision-adjustment operator immediately for each new abstract state (line 7) instead of only before expanding an abstract state.

• 4. CPA++ attempts a forced covering by calling $\mathsf {fcover}$ before expanding an abstract state (lines 3–5).

The first two changes allow calling CPA++ iteratively and keep expanding the same set of abstract states, which is necessary for CEGAR with lazy abstraction (where we want to abort as soon as we find an abstract error state and continue after refinement without restarting from scratch; $\mathsf {abort}(e)$ is typically implemented to return $true$ if $e$ is an abstract state at error location ${ l _ ERR }$). The new position of the call to the precision-adjustment operator is necessary because previously the resulting abstract states ($\widehat{e}$ in Algorithm 1) were never put into $\mathsf {reached}$. However, we need the abstract states resulting from $\mathsf {prec}$ to be in $\mathsf {reached}$, because among them are the abstraction states of the Predicate CPA, which are necessary for refinement.

Similar changes to the CPA algorithm have been used previously [22, 25]; we now combine them in order to provide an all-encompassing algorithm for reachability that we can use as building block for our unifying framework for predicate-based software verification.

4 Unifying SMT-Based Approaches for Software Verification

In this section, we will give a unifying overview of four widely used approaches to software verification: bounded model checking (BMC), k-induction, predicate abstraction, and the Impact algorithm. We reformulate the approaches in our theoretical framework from the previous section and illustrate their differences using our example program.

In the following, the Predicate CPA $\mathbb {P}$ is always combined with at least the CPA $\mathbb {L}$ for program-counter tracking and the ARG CPA $\mathbb {A}$ for tracking the predecessor–successor as well as coverage relations between ARG nodes. We show relations between ARG nodes graphically in the figures and omit them for ease of presentation when notating abstract states as tuples. For path formulas, we use a skolemized notation based on SSA indices [39], which is easier to read than existential quantification of many variables. Index addition and removal is done implicitly when converting between abstraction formulas and path formulas.

4.1 Bounded Model Checking

For bounded model checking, we set the ABE block size to infinite (we call this whole-program encoding) by using the block operator $\mathsf {blk}^{{ never}}$, and we use $\mathsf {fcover}^{{ id}}$ (i.e., no forced coverings). Additionally, we combine the Predicate CPA with a CPA for bounding the state space besides the typical basic CPAs.

The Loop-Bound CPA $\mathbb {LB}$ tracks in its abstract states for every loop of the program how often the loop body was traversed on the current program path. It associates each loop-head location with a counter that starts with −1 and is incremented by the transfer relation whenever the respective location is reached. The precision is the loop bound k: $\pi = k$, with $k>0$. The transfer relation of the Loop-Bound CPA is unsound on purpose: it does not produce any successor abstract states for abstract states in which one of the counters for the loop-head locations is equal to the loop bound k in the precision and thus prevents the analysis from exploring any paths for more than k loop iterations. Apart from that, the Loop-Bound CPA uses the standard operators $\mathsf {merge}^ sep$, $\mathsf {stop}^ sep$, and $\mathsf {prec}^{{ id}}$.

This configuration leads to an analysis without abstraction computations, expensive coverage checks, and refinements. Instead, the CPA++  algorithm simply unrolls the CFA (within the loop bound), and each abstract state contains a path formula that exactly represents the paths from the initial location to this abstract state. We wrap the CPA++  algorithm in another algorithm that checks satisfiability of the path formula of each abstract error state after the CPA++  algorithm has finished (we can use Algorithm 3, which is discussed in Sect. 4.2, for this by omitting lines 15–23). If at least one path formula is satisfiable (for efficiency, we check the disjunction of all path formulas at once in line 10 of Algorithm 3), then there exists a feasible path to the error location, i.e., the specification is violated.

We can also implement a forward-condition check [44] by making an additional SMT query for the satisfiability of the path formulas of all those abstract states for which the Loop-Bound CPA has unsoundly restricted the successor abstract states. If none of these path formulas is satisfiable, the specification is proven to hold for the program. If for a given loop bound k the result was inconclusive (i.e., no specification violation found but the forward-condition check was unsuccessful, too), we can repeat the bounded model check with a higher k.

Fig. 5

ARG for applying BMC to the example of Fig. 2

4.2 k-Induction

For ease of presentation, we assume here that the loop head is not reachable from the error location ${ l _ ERR }$ and that the analyzed program has exactly one loop whose loop-head location is $l _{{ LH}}$. In practice, k-induction can be applied to programs with many loops [13].

k-Induction, like BMC, is an approach that at its core does not rely on abstraction techniques. We present an algorithm for k-induction-based verification based on the Predicate CPA as Algorithm 3. This algorithm supports iterative deepening and injection of continuously refined invariants. We can use this algorithm in combination with (external) standard invariant-generation techniques, such as data-flow analysis [57, 63] and template-based approaches [16, 36]. This is necessary, because often the safety property of a verification task is not directly k-inductive for any k, but only relative to some auxiliary invariant, so that plain k-induction cannot succeed in proving safety. Strengthening the hypothesis of the inductive-step case with auxiliary invariants may allow the algorithm to prove such properties as well.

Algorithm 3 gets as input initial and maximal values for the loop bound and a function that computes the next loop bound after each iteration (this function can for example increase the value by one, or double it). Additionally we give the algorithm a combination of CPAs (as a composite CPA) that includes the Location CPA $\mathbb {L}$ (cf. Sect. 2.2), our Predicate CPA $\mathbb {P}$ in the configuration for bounded model checking, and the Loop-Bound CPA $\mathbb {LB}$ (cf. Sect. 4.1). Thus, each abstract state is a tuple of the current program counter $l$ (this is an abstract state of $\mathbb {L}$), a predicate abstract state (which is itself a tuple of an abstraction formula, an abstraction location, and a path formula), and a mapping of loop heads to loop counters (this is an abstract state of $\mathbb {LB}$).

For each value of the loop bound k as determined by the initial and maximal values and the increment function, the algorithm performs the checks for base case, forward condition, and step case. For the base case (lines 6–11), which is identical to bounded model checking, we set the bound of the Loop-Bound CPA to k and use the CPA++ algorithm (Algorithm 2) to unroll the program with an abstract state $e_ INIT$ at the initial program location as initial abstract state and the precision $\pi _ INIT$ as initial precision (the Location CPA has an empty precision, the Predicate CPA has a precision that maps all program locations to an empty set of predicates, and the Loop-Bound CPA has a precision that consists of the single constant value k). Then we create a disjunction of the path formulas of all resulting abstract states at the error location. Because of the configuration of the Predicate CPA and the Loop-Bound CPA, this formula represents all paths from ${ l _ INIT }$ to ${ l _ ERR }$ that visit the loop body at most k times. If this formula is feasible, ${ l _ ERR }$ is reachable and the algorithm terminates.

For the forward condition (lines 12–14), we check in a similar manner whether the loop-head location $l _{{ LH}}$ is reachable at the start of the $k+1^{\mathrm{st}}$ loop iteration. If this is not the case, this implies that the error location is also not reachable in the $k+1^{\mathrm{st}}$ loop iteration (or later on), and thus the program is safe and the algorithm terminates.

For the inductive-step case (lines 15–23), we again use the CPA++ algorithm to unroll the program, though this time with a loop bound of $k+1$ and an abstract state at the loop head as initial abstract state. For the following satisfiability check, we use the disjunction of the path formulas of all abstract states at the error location and with a loop-counter value of k (i.e., in the $k+1^{\mathrm{st}}$ loop iteration). Note that because we assume that the loop body cannot be reached from the error location ${ l _ ERR }$, this formula represents all paths with k safe loop iterations and a specification violation in the $k+1^{\mathrm{st}}$ iteration. Additionally, we strengthen the hypothesis of the inductive-step case with the currently known loop invariant that is produced by the concurrently running (external) invariant generator. The invariant obtained from the invariant generator is an SMT formula that is guaranteed to hold at the loop-head location. If the invariant generator produces a stronger loop invariant while the inductive-step case is running, we immediately try again with the new invariant (this can be done efficiently using an incremental SMT solver). If the inductive-step case succeeds, the program is safe and the algorithm terminates. Otherwise, we repeat with a larger value of k, which is called iterative deepening.

Fig. 6

ARG for the inductive-step case of k-induction applied to the example of Fig. 2

4.3 Lazy Predicate Abstraction

Predicate abstraction with counterexample-guided abstraction refinement (CEGAR) does not use a loop bound, but attempts to converge by determining whether new abstract states are covered by any existing abstract state. In order to make the coverage checks efficient, the abstraction formula of an abstract state overapproximates the reachable concrete states using a boolean combination of predicates over program variables from a given mapping from program locations to sets of predicates (the precision $\pi$). This abstraction is computed by an SMT solver and the result (the abstraction formula $\psi$) is stored as a BDD, which can be efficiently checked for entailment. With ABE, the abstraction computations and coverage checks are done only at block ends. For the CPA++ algorithm to terminate it has to be ensured that all ABE blocks do not contain potentially infinite paths, e.g., by using $\mathsf {blk}^{l}$ to let blocks end at loop-head locations. For predicate abstraction we do not use forced coverings.

Furthermore, we wrap our CPA++  algorithm (Algorithm 2) inside Algorithm 4, which implements CEGAR by alternately calling the CPA++  algorithm in order to expand the abstract model and a refinement operator in order to refine the precision of the analysis. We give it a composite CPA that consists of the Location CPA $\mathbb {L}$, the ARG CPA $\mathbb {A}$ (necessary for constructing abstract paths during refinement), and the Predicate CPA $\mathbb {P}$. Using CEGAR and the predicate-refinement strategy of the refinement operator $\mathsf {refine}_\mathbb {P}$, it is often possible to find a suitable precision automatically, starting with an empty initial precision. First, CEGAR uses the CPA++ algorithm in order to create the abstract model of the program. If the analysis encounters an abstract state at error location ${ l _ ERR }$, we pause the state-space exploration done by CPA++ algorithm (via the function $\mathsf {abort}_ ERR$) and start the refinement using $\mathsf {refine}_\mathbb {P}$. As described in Sect. 3.2, this operator reconstructs the concrete program path leading to the abstract state at ${ l _ ERR }$ and checks the path for feasibility using an SMT solver. If the concrete error path is feasible, we terminate the analysis. Otherwise, the precision is refined (by employing an SMT solver to compute Craig interpolants [38] for the locations on the error path), and the CPA++ algorithm is restarted with adjusted sets $\mathsf {reached}$ and $\mathsf {waitlist}$. Due to the refined precision, it is guaranteed that the previously identified infeasible error paths are not encountered again. This process is iterated until either a feasible concrete error path is found, or the CPA++ algorithm terminates proving the program safe.

Fig. 7

ARG for predicate abstraction applied to the example of Fig. 2; highlighted nodes are abstraction states

4.4 Lazy Abstraction with Interpolants (Impact)

Lazy abstraction with interpolants [61], more commonly known as the Impact algorithm due to its first implementation in the tool Impact, was originally presented as an algorithm that repeatedly executes the steps Expand (discovery of new abstract states), Refine (strengthening of abstract states using interpolation), and Cover (detecting coverage between abstract states). Later on it was reformulated in a unified framework together with predicate abstraction and enhanced with ABE [25]. Our description here is based on this reformulation, which was shown to behave similarly to the original algorithm. Like for predicate abstraction, for Impact we use CEGAR (Algorithm 4), the CPA++ algorithm, and the Predicate CPA, however, we configure the latter differently. Compared to predicate abstraction, $\pi$ stays always empty because the Impact refinement strategy of $\mathsf {refine}_\mathbb {P}$ is used. Thus, the abstraction computation at block ends always trivially returns $true$. The Impact refinement strategy, however, makes use of the fact that interpolants are guaranteed to hold at their specific location in the error path and directly strengthens the abstraction formulas of abstract states along the error path with the respective interpolants. The abstract error state is removed during refinement and all coverage relations involving the strengthened abstract states are rechecked after refinement. Furthermore, the abstraction formulas $\psi$ are stored syntactically and coverage is checked using an SMT solver, instead of BDD entailment. If desired, we can configure $\mathsf {fcover}_\mathbb {P}$ to perform interpolation-based forced covering as an optimization (cf. Sect. 3.3). Impact avoids the costly abstraction computations and rediscovery of abstract states, at the expense of more costly coverage checks.

Fig. 8

Final ARG for applying the Impact approach to the example of Fig. 2; highlighted nodes are abstraction states

4.5 Summary

We showed how to express four approaches to software verification with our framework for predicate-based analyses and illustrated how they work on the example from Fig. 2. Table 1 summarizes the choices that need to be made for each of the approaches. While BMC is limited in its capacity of proving correctness, it is also the most straightforward of the four approaches, because k-induction requires an auxiliary-invariant generator to be applicable in practice, and predicate abstraction and Impact require interpolation techniques. While the invariant generator and the interpolation engine are usually treated as black box in the description of these approaches, the efficiency and effectiveness of the techniques depends on the quality of these modules.

4.5.1 Further Algorithms

There are other approaches for software verification besides the four that we unify in this work, and of course, the best features of all approaches can be combined into new, “hybrid” methods, such as implemented in CPAchecker [71], SeaHorn [48], and Ufo [3]. The focus of this article is not to find the best possible combination, but to study the approaches in isolation. In the following, we briefly discuss the most important SMT-based approaches, ordered roughly accordingly to how similar they are to the approaches that we have discussed so far.

The Ufo algorithm [2] combines the Impact algorithm with predicate abstraction. Ufo is similar to Impact, but implements a choice between performing predicate-abstraction computation when creating fresh abstract states and initializing them with $true$ as Impact does. Refinement is done using interpolation, and the interpolants can be used to either strengthen the abstract states (pure Impact behavior), or to update the set of predicates (pure predicate-abstraction behavior), or do both. This approach can be seen as an instantiation of our framework with a refinement operator that uses both the Impact- and the predicate-refinement strategies (cf. Sect. 3.2).

Symbolic execution [58] follows each path in the program separately and interprets its operations; the abstract states track explicit and symbolic values of program variables in a symbolic store as well as constraints over the symbolic values. If a variable is assigned a nondeterministic value, a fresh symbolic value is stored; if an explicit value can be determined by the analysis, then the explicit value is stored. Constraints that are encountered along a path are tracked and checked for satisfiability, using the symbolic store as interpretation, whenever the feasibility of the path needs to be determined (e.g., if an error location is reached). The framework presented in this work can be configured as an analysis that behaves similarly to symbolic execution (just without symbolic store) by using the CPA algorithm with the Predicate CPA configured to use $\mathsf {blk}^{{ never}}$ and $\mathsf {merge}^ sep$ instead of $\mathsf {merge}_\mathbb {P}$. The operator $\mathsf {blk}^{{ never}}$ has the effect of disabling abstraction computations and thus accumulating the semantics of all program operations of a path in the path formula of abstract states during traversal (as for BMC). The operator $\mathsf {merge}^ sep$ has the effect of preventing all merges between abstract states and thus keeping all paths separate, forming a reachability tree. Note that differently from symbolic execution this configuration tracks all values syntactically.

Table 1 Configuration of the predicate CPA $\mathbb {P}$ for the four approaches

Slicing abstractions [30, 43] (a.k.a. “state splitting”) starts with an abstract-reachability graph in which all abstract states are labeled with $true$. The algorithm iteratively searches for an infeasible error path in this graph and computes interpolants for the respective path. The strategy for refining the abstract model consists of duplicating each abstract state for which an interpolant was found (including its edges) and conjoining the interpolant to one of the resulting abstract states and the negated interpolant to the other one (“state splitting”). Then all edges of both resulting states are checked for feasibility. This always results in enough edges being removed such that the current infeasible error path no longer exists in the abstract-reachability graph. This is repeated (CEGAR) until either no infeasible error path exists anymore, or a feasible error path is found. The approach of splitting abstract states has also been extended to a combination of predicate abstraction and explicit-value analysis [49], similar to the combination of lazy predicate abstraction and explicit-value analysis [22].

Trace abstraction [50] is a CEGAR-based approach in which the iteratively refined abstract model of the program is not a set of abstract states, but instead an automaton that represents an overapproximation of the feasible paths of the program. Every time a spurious counterexample is detected, a trace automaton that represents a set of infeasible paths including the current counterexample is created using interpolation, and this trace automaton is subtracted from the current abstract model.

Software proof-based abstraction with counterexample-based refinement (SPACER) [59] is an approach that combines CEGAR with its dual, proof-based abstraction (PBA) [62]. While CEGAR maintains an overapproximation of the program and refines it using infeasible error paths, PBA maintains an underapproximation and refines it if it finds a safety proof that holds only for the underapproximation but not for the original system. SPACER follows the PBA approach but uses an abstraction of the underapproximation to allow handling infinite-state systems and refines this abstraction using CEGAR.

Model checking modulo theories (MCMT) [45, 46] is an approach that focuses on verifying infinite-state systems that use arrays. It is based on a backwards-reachability analysis and SMT solving for theories that fulfill certain conditions. MCMT has been combined with CEGAR and interpolation to define an analysis that can be described as a backwards variant of Impact and applied to software model checking [4]. This approach uses interpolation to compute quantifier-free interpolants for a restricted class of formulas with arrays and can prove universally quantified properties over arrays automatically.

IC3 [28], which is also known as property-directed reachability (PDR) [42], is an algorithm for model checking finite-state systems. It aims at producing an inductive invariant that is strong enough to prove safety by incrementally learning clauses that are inductive with regard to the previously learned clauses. Such clauses are derived by generalizing from counterexamples to induction proofs. PDR was originally designed for boolean transition systems and based on SAT solving. It has been generalized from boolean systems to SMT [52] and applied to software in various ways [27, 32, 33, 54], which we discuss in the following. If PDR is combined with an explicit (instead of symbolic) tracking of the program counter, this lets the algorithm produce an abstract-reachability tree [32]. In fact, because the sets of clauses that PDR learns fulfill the properties of interpolants, this tree-based PDR can even be seen as a version of Impact, just with a different way of producing interpolants. A hybrid approach that uses both a regular interpolation engine as well as PDR for producing interpolants is also possible [32]. It would be an interesting extension of our Predicate CPA to adopt the clause-learning strategy of PDR as an alternative to using interpolation during refinement (cf. Sect. 3.2). Another approach for software verification using PDR is to define a boolean abstract model of the program using predicate abstraction and use an almost unchanged PDR algorithm for verifying the abstract model [33]. The abstraction is refined using typical predicate-discovery strategies (e.g., interpolation) whenever an infeasible error path is found. CTIGAR [27] is an approach for applying PDR to software that does not rely on CEGAR (i.e., using error paths for refinement), but uses counterexamples to induction (CTI) for abstraction refinement. CTIGAR computes abstract CTIs from the concrete CTIs of PDR by using predicate abstraction and refines the abstraction using interpolation if it finds a clause that is inductive with regard to the previously learned clauses, but its abstract version is not. PDR can also be extended from standard induction to property-directed k-induction [54]. This allows it to more easily verify programs for which useful 1-inductive invariants are cumbersome and difficult to find, while more concise k-inductive invariants exist.

Loop invariants that are strong enough to verify program safety can also be computed via abduction [40]. Similar to the PDR-based approaches, a candidate invariant is strengthened until it becomes inductive. However, while PDR starts from facts that are known to hold, the abductive approach starts from the conjecture it wants to prove and asks an abduction engine to generate candidate strengthenings that would allow the conjecture to hold. Then it needs to check whether one of the candidates holds, which may need further recursive strengthenings with backtracking. As abduction engine, it is possible to use for example quantifier elimination in Presburger arithmetic.

5 Evaluation

We evaluate BMC,  k-induction, predicate abstraction, and Impact on a large set of verification tasks and compare the approaches.

5.1 Benchmark Set

As benchmark set we use the verification tasks from the 2017 Competition on Software Verification (SV-COMP’17) [10]. We used only verification tasks where the property to verify is the reachability of a program location (excluding the properties for memory safety, overflows, and termination, which are not in our scope). From the remaining set of verification tasks, we excluded the categories ReachSafety-Arrays, ReachSafety-Floats, ReachSafety-Recursive, and ConcurrencySafety, each of which is not supported by at least one of our implementations of the approaches. The resulting set of categories consists of a total of 5287 verification tasks from the subcategory DeviceDriversLinux64_ReachSafety of the category SoftwareSystems and from the following subcategories of the category ReachSafety: Bitvectors, ControlFlow, ECA, Floats, Heap, Loops, ProductLines, and Sequentialized. A total of 1374 tasks in the benchmark set contain a known specification violation, while the rest of the tasks is assumed to be free of violations.

5.2 Experimental Setup

Our experiments were conducted on machines with one 3.4GHz CPU (Intel Xeon E3-1230 v5) with 8 processing units and 33GB of RAM each. The operating system was Ubuntu 16.04 (64 bit), using Linux 4.4 and OpenJDK 1.8. Each verification task was limited to two CPU cores, a CPU run time of 15 min, and a memory usage of 15GB. We used the benchmarking framework BenchExec ⁴ [23] to perform our experiments. We used version 1.6.18-jar17 of CPAchecker, with MathSAT5 as solver for all SMT queries. We configured CPAchecker to use the SMT theories of equality with uninterpreted functions, bit vectors, and floats. For Impact and predicate abstraction, an ABE block size needs to be chosen: we used $\mathsf {blk}^l$ to let blocks end at loop heads. For Impact we also activated the forced-covering optimization with $\mathsf {fcover}^{\textsc {Impact}}$. For BMC we used a configuration with forward-condition checking [44]. For BMC and k-induction, we used an initial bound of $k=1$ and an increment function ${ inc}(n)=n+1$. Auxiliary invariants are provided to k-induction using a continuously refining data-flow analysis from existing work [14] that uses disjunctions of intervals as its abstract domain. We configure CPAchecker to avoid false alarms by validating the feasibility of each found error path using Cbmc 5.6. Time results are rounded to two significant digits.

5.3 Reproducibility

All presented approaches are implemented in the open-source verification framework CPAchecker [20], which is available under the Apache 2.0 license. All experiments are based on publicly available benchmark verification tasks [10]. Tables with our detailed experimental results are available on the supplementary web page.⁵

5.4 Experimental Validity

5.4.1 Internal Validity

We implemented all evaluated approaches using the same software-verification framework: CPAchecker. This allows us to compare the actual algorithms instead of comparing different tools with different front ends and different utilities, thus eliminating influences on the results caused by implementation differences that are unrelated to the actual algorithms.

To ensure technical accuracy, we used the open-source benchmarking framework BenchExec ⁶ [23] for conducting our experiments.

5.4.2 External Validity

We perform our experiments on the largest, most diverse, and publicly available collection of verification tasks,⁷ which is also used by the international competition on software verification.

Table 2 Experimental results of the approaches for all 5287 verification tasks, 1374 of which contain bugs, while the other 3913 are considered to be safe

Fig. 9

Quantile plots for all correct proofs and alarms

5.5 Results Overall

Table 2 shows the number of correctly solved verification tasks for each of the approaches, as well as the time that was spent on producing these results. None of the approaches reported incorrect proofs⁸ or incorrect alarms. When an algorithm exceeds its time or memory limit, it is terminated inconclusively. Other inconclusive results occur, for example, if the implementation encounters an unsupported feature, such as recursion, or if during an SMT query, an error occurs in the SMT solver. When comparing k-induction to the other techniques, there is sometimes a chance that the other techniques must give up due to an unsupported feature, while k-induction is not encountering the unsupported feature because it is waiting for the invariant generator to generate a strong invariant. Therefore, k-induction has fewer other inconclusive results but instead more timeouts than predicate abstraction and Impact. The quantile plots in Fig. 9 show the accumulated number of successfully solved verification tasks within a given amount of CPU time. A data point (x, y) of a graph means that for the respective configuration, x is the number of correctly solved tasks with a CPU run time of less than or equal to y seconds.

5.5.1 BMC

As expected, BMC produces both the fewest correct proofs and the most correct alarms, confirming BMC’s reputation as a technique that is well suited for finding bugs. Having the fewest solved tasks, BMC also accumulates the lowest total CPU time for correct results. Its average CPU time spent on correct results is also lower than for the other techniques: for proofs, BMC often fails to provide a correct result while the other approaches spend a lot of time on successfully finding a proof; for finding bugs, its straightforward approach outperforms the abstraction techniques while k-induction unnecessarily invests time in generating auxiliary invariants. On average, BMC spends 1.2 s on formula creation, 3.5 s on SMT-checking the forward condition, and 7.4 s on SMT-checking the feasibility of error paths.

5.5.2 k-Induction

The slowest technique is k-induction with continuously refined invariant generation, which is the only technique that effectively uses both available cores by running the auxiliary-invariant generation in parallel to the k-induction procedure, thus spending significantly more CPU time than the other techniques, while the wall time it spends is comparable to the wall time spent by the abstraction techniques for correct proofs. Compared to BMC, k-induction spends additional time on building the step-case formula and generating auxiliary invariants, but can often prove safety by induction without unrolling loops. Considering that over the whole benchmark set, k-induction generates the highest overall number of correct results, the additional effort appears to be mostly well spent. On average, k-induction spends 1.2 s on formula creation in the base case, 2.5 s on SMT-checking the forward condition, 3.0 s on SMT-checking the feasibility of error paths, 9.3 s on creating the step-case formula, 14 s on SMT-checking inductivity, and 20 s on generating auxiliary invariants, which shows that the inductive-step case requires much more effort than the base case and also about 3 s more than for invariant generation. For tasks containing actual bugs, however, this effort is wasted, which explains why k-induction spends not only more CPU time but also significantly more wall time on correct alarms than the other techniques.

5.5.3 Predicate Abstraction and Impact

Predicate abstraction and Impact both perform similarly for finding proofs, which matches the observations from earlier work [25]. An interesting difference is that Impact finds more bugs. We attribute this observation to the fact that abstraction in Impact is lazier than with predicate abstraction, which allows Impact to explore larger parts of the state space in a shorter amount of time than predicate abstraction, causing Impact to find bugs sooner. For verification tasks without specification violations, however, the more eager predicate-abstraction technique pays off, because it avoids many SMT-checks for determining coverage. Although in total, both abstraction techniques have to spend similar effort, this effort is distributed differently across the various steps: While, on average, predicate abstraction spends more time on computing abstractions (23 s) than the Impact algorithm spends on deriving its abstraction by interpolation (9.0 s), the latter requires the relatively expensive forced-covering step (12 s).

Fig. 10

Quantile plots for some of the categories

5.6 Results on Selected Categories

Although the plot in Fig. 9a suggests that k-induction with continuously refined invariants outperforms the other techniques in general for finding proofs, a closer look at the results in individual SV-COMP categories reveals that the performance of an algorithm strongly depends on the type of verification task, but also reconfirms the observation of Fig. 9b that BMC consistently performs well for finding bugs.

For example, on the safe tasks of the category on Linux device drivers, k-induction performs worse than predicate abstraction and Impact (Fig. 10a). These device drivers are often large in size, containing pointer arithmetic and complex data structures. The interval-based auxiliary-invariant generator that we used for k-induction is not a good fit for this kind of problems, and a lot of effort is wasted, while the abstraction techniques are often able to quickly determine that many operations on pointers and complex data structures are irrelevant for the safety property. We did not include the plot for the correct alarms in the category on device drivers, because each of the approaches only solves about 30 tasks, i.e., there is not enough data among the correct alarms to draw any further conclusions.

The quantile plot for the correct proofs in the category of event condition action systems (ECA) is displayed in Fig. 10b. BMC is hardly visible in this figure, because there is only a single task in the category that it could unroll exhaustively. Each of these tasks only consists of a single loop, but these loops contain complex branching structures over many different integer variables, which leads to an exponential explosion of paths, such that checking satisfiability of an SMT formula representing an unwinding of such a loop is often expensive in terms of time and memory. Also, because in many tasks of this category almost all of the variables are in some way relevant to the reachability of the error location within this complex branching structure, the abstraction techniques are unable to come up with useful abstractions and perform poorly. The interval-based auxiliary-invariant generator that we use for k-induction, however, appears to provide useful invariants for handling the complexity of the control structures, and the state-machine-like nature of these tasks requires the consideration of many different cases and their interaction across consecutive loop iterations, such that k-induction performs much better than all other techniques in this category. We did not include the plot for the correct alarms in this category, because the abstraction techniques were not able to detect a single bug, and only BMC and k-induction detect one single bug for the same task, namely Problem10_label46_false-unreach-call.c.

Figure 10c shows the quantile plot for correct proofs in the category on product lines. In this category, as in Fig. 9a, k-induction slightly outperforms the other techniques in the number of found proofs but it also becomes even more apparent than in other categories how much slower than the other techniques it is (on average for correct results). Figure 10d shows the quantile plot for correct alarms in the same category. It is interesting to observe that Impact distinctly outperforms predicate abstraction on the tasks that require over 40 s of CPU time, whereas in the previous plots, the differences between the two abstraction techniques were either hardly visible or Impact performed worse than predicate abstraction. While, as shown in Fig. 10c, both techniques report almost the same amount of correct proofs (317 for predicate abstraction, 315 for Impact), Impact detects 130 bugs, whereas predicate abstraction detects only 125. This seems to indicate that the state space spanned by the different product-line features can be explored more quickly by lazy abstraction of Impact than with the more eager predicate abstraction.

5.7 Results on Selected Verification Tasks Showing Individual Strengths

The previous discussion showed that while overall, the approaches perform rather similar (apart from BMC being inappropriate for finding proofs, which is expected), each of them has some strengths due to which it outperforms the other approaches on certain programs. In the following, we will list some examples from various categories of SV-COMP that were each solved by one of the approaches, but not by the others, and give a short explanation of the reasons.

5.7.1 BMC

Only BMC finds a bug in task const_false-unreach-call1.i (23 s, Category Loops), and only BMC proves, by exhaustively unrolling a loop, safety for the task pals_opt-floodmax.4_true-unreach-call.ufo.BOUNDED-8.pals_true -termination.c (310 s, Category Sequentialized). Both of these tasks have in common that they contain bounded loops. The bounded loops are a good fit for BMC and enable it to prove correctness; k-induction, which in theory is at least as powerful as BMC, spends too much time trying to generate auxiliary invariants and exceeds the CPU time limit before solving these tasks.

5.7.2 k-Induction

k-Induction outperforms the other techniques on many of the state-machine-like tasks of the category on event condition action systems (ECA). Only k-induction proves correctness of the task Problem14_label00_true-unreach-call.c (14 s, Category ECA), which, like all tasks in that category, encodes a complex state machine, i.e., a loop over switch statements with many cases, which in turn modify the variable that is considered by the switch statement. The loop is unbounded, such that BMC cannot exhaustively unroll it, and the loop invariants that are required to prove correctness of the task need to consider the different cases and their interaction across consecutive loop iterations, which is beyond the scope of the abstraction techniques but easy for k-induction (cf. [13] for a detailed discussion of a similar example).

5.7.3 Predicate Abstraction

Only predicate abstraction solves verification task toy_true-unreach-call_false- termination.cil.c (65 s, Category Sequentialized). The task consists of an unbounded loop that contains a complex branching structure over integer variables, most of which only ever take the values 0, 1 or 2. Interpolation quickly discovers the abstraction predicates over these variables that are required to solve the task, but in this example, predicate abstraction profits from eagerly computing a sufficiently precise abstraction early after only 10 refinements while the lazy refinement technique used by Impact exceeds the time limit after 165 refinements, and the invariant generator used by k-induction fails to find the required auxiliary invariants before reaching the time limit.

5.7.4 Impact

Only Impact solves Problem05_label50_true-unreach-call.c (190 s, Category ECA). BMC fails on this task due to the unbounded loop, and the invariant generator used by k-induction does not come up with any meaningful auxiliary invariant before exceeding the time limit. Predicate abstraction exceeds the time limit after only four refinements, and up to that point, 90% of its time is spent on eagerly computing abstractions. The lazy abstraction performed by Impact, however, allows it to progress quickly, and the algorithm finishes after 9 refinements.

6 Conclusion

This paper presents a comparative study of four state-of-the-art approaches for SMT-based software verification. First, we define a configurable program analysis for the predicates domain, which serves as the unifying core component of our comparison framework. Second, we express each approach in our framework by a specific set of parameters and illustrate the effect on how the state-space exploration is performed. Third, we provide the results of a thorough experimental study on a large number of verification tasks, in order to show the effect and performance of the different approaches, including a detailed discussion of particular verification tasks that can be solved by one approach while all others fail. In conclusion, there is no clear winner: there are disadvantages and advantages for each approach. We hope that our conceptual and experimental overview is useful and contributes to understanding the difference of the approaches and the potential application areas.