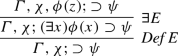Skip to main content
SpringerLink
Log in

Human-Centered Automated Proof Search

  • Published:
Journal of Automated Reasoning Aims and scope Submit manuscript

Abstract

Human-centered automated proof search aims to capture structures of ordinary mathematical proofs and discover human strategies that are used (implicitly) in their construction. We analyze the ways of two theorem provers for approaching that goal. One, the G&G-prover, is presented in Ganesalingam and Gowers (J Autom Reason 58(2):253–291, 2017); the other, Sieg’s AProS system, is described in Sieg and Walsh (Rev Symb Logic 1-35, 2019). Both systems make explicit, via their underlying logical calculi, the goal-directedness and bi-directionality of proof construction. However, the calculus for the G&G-prover is a weak fragment of minimal first-order logic, whereas AProS uses complete calculi for intuitionist and classical first-order logic. The strategies for the construction of proofs are dramatically different as well. The G&G-prover uses a waterfall strategy and is thus restricted to problems that can be solved without backtracking. The AProS strategies, by contrast, support a complete search procedure with backtracking. These divergences are rooted in the fact that the concrete goals of the systems are different: The G&G-prover is to yield write-ups indistinguishable from good mathematical writing; AProS is to yield humanly intelligible formal proofs by logically and mathematically motivated strategies. In our final Programmatic remarks, we sketch a plausible, but difficult project for achieving more fully G&G’s broad goals by radically separating proof search from proof translation: one could use AProS for the proof search and then exploit the strategic structure of the completed proof as the deterministic underpinning for its translation into a natural language.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

Notes

  1. See Harrison et al. [20] for a more comprehensive view on the history of interactive theorem proving.

  2. On the discovery of this problem, which Hilbert did not include in the official Paris list, see [55].

  3. For Gowers, there was also a deep educational motivation that was forcefully expressed in an interview with the Notices of the American Mathematical Society reported in Diaz Lopez [11]. Sieg’s AProS project originally had a more restricted educational goal; for reaching even that goal, a human-centered proof search procedure was needed; see Sieg [46]. These matters are briefly discussed in our concluding Programmatic remarks.

  4. That point was made vivid to WS through [40] and Andrews’ efforts in [1] to associate natural deduction proofs with mating proofs. (WS served on Pfenning’s thesis committee and conducted a seminar on automated proof search with Andrews in the early 1990s.) According to (Andrews [2], p. 285), it was Larry Wos in [60] who “drew attention to the importance of investigating mappings between (a) clause representation and natural deduction representation of proofs and (b) corresponding search strategies”.

  5. These NI calculi are situated properly between sequent and natural deduction calculi. Their rules are formulated in Appendix 1. The general idea of “bi-directional” is that of “forward” and “backward chaining”. The precise meaning of the term depends on the graphical representation of proofs. In case of the tree-representation of NIC proofs, the directions are “left to right” and “right to left”, whereas in the Fitch-representation they are “top down” and “bottom up”. See Sect. 2, but also Sect. 4, where the (direction of) distinct strategic steps are discussed in detail.

  6. The proof of the other theorem, obtained by AProS, is presented in the second appendix of Sieg and Walsh [53]. That ”other” proof was given in Ganesalingam and Gowers [14].

  7. The methodological reason is a parallelism to Hilbert [23], where groups of axioms were formulated for each basic notion. The significance of derived rules for capturing argumentation is emphasized in Hilbert and Bernays ([26], p. 139) and is explicit in Bernays [4], where rule-based formulations of the sentential calculus of Principia Mathematica are given. Gentzen ([18], p. 514) calls inference rules the “formal counterpart” of an informal reasoning step.

  8. Cf. [58] and [47]. The Urdissertation was probably written in the fall or winter of 1932. The real dissertation [17] was submitted for publication on 21. July 1933.

  9. Gentzen repeats these remarks almost literally in (Gentzen [17], p. 176) and re-asserts on p.183, “Wir wollen einen Formalismus aufstellen, der möglichst genau das wirkliche logische Schließen bei mathematischen Beweisen wiedergibt.”

  10. Here is the German text of the quotation: Die Formalisierung des logischen Schliessens bei Russell, Hilbert, Heyting (für das intuit. Schliessen) u.a. entfernt sich ziemlich weit von der Art des Schliessens, wie sie in Wirklichkeit (etwa bei zahlentheoretischen Beweisen) geübt wird. Dafür werden beträchtliche formale Vorteile erzielt. Ich will zunächst einmal einen Formalismus (“Kalkül N1J”) aufstellen, der dem wirklichen Schliessen möglichst nahe kommt. Es ist doch anzunehmen, dass auch ein solcher gewisse Vorteile hat, und ich glaube, auf Grund meiner weiteren Ergebnisse behaupten zu können, dass dies der Fall ist.

  11. (Gentzen [17], p. 177). Gentzen continues by claiming that the Hauptsatz is valid for both intuitionist and classical logic, but for stating and proving it in a “convenient form” he had to introduce a special calculus, the sequent calculus. “Hierzu erwies sich der natürliche Kalkül nicht als geeignet. Zwar weist er schon die für die Gültigkeit des Hauptsatzes wesentlichen Eigenschaften auf, doch nur in seiner intuitionistischen Form, während der Satz vom ausgeschlossenen Dritten, ..., im Hinblick auf diese Eigenschaften eine Sonderstellung einnimmt.”

  12. Here is the German text of the quotation: Der Hauptsatz besagt, daß sich jeder rein logische Beweis auf eine bestimmte, übrigens keineswegs eindeutige, Normalform bringen läßt. Die wesentlichsten Eigenschaften eines solchen Normalbeweises lassen sich etwa so ausdrücken: Er macht keine Umwege. Es werden in ihm keine Begriffe eingeführt, welche nicht in seinem Endergebnis enthalten sind und daher zu dessen Gewinnung notwendig verwendet werden müssen.

  13. Prawitz [43] establishes the Hauptsatz or the normalization theorem also for (a subtly restricted, but equivalent form of) classical logic. There are further remarkable results in that work. Let us mention two: (1) “branches” in normal proofs can be uniquely divided into E- and I-parts, where only elimination rules are used in the E-part and only introduction rules in the I-part; (2) “contradictory pairs” of formulae are restricted to pairs with the negated component being a positive subformula of an assumption. Those features inform the AProS strategies for proof search in a crucial way.

  14. For example, Melvin Fitting wrote in his (Fitting [13], p. 95): “Hilbert systems are inappropriate for automated theorem proving. The same applies to natural deduction, since Modus Ponens is a rule in both.” Only a few intrepid philosophical and psychological souls tried to use natural deduction calculi for automated proof search; among them were Pelletier, Pollock, and Rips; see [37, 42] and [44]. The special issue of Studia Logica [41] was devoted to natural deduction; at the time, that was the best we could do to reflect work relating natural deduction and theorem proving.

  15. See [8, 10, 45, 49, 52], and [50].

  16. Troelstra and Schwichtenberg remark in their (Troelstra and Schwichtenberg [56], pp. 32, 60) that normality of natural deduction derivations is a “global property” as it involves “the order in which the rules are applied.” They took this fact as a reason for considering and investigating sequent calculi. We take it as a reason for locally exploiting the constraints on rule applications in (automated) proof search.

  17. Prawitz ([43], Appendix C, section 1) points to Jaśkowski [30] as a second root for natural deduction calculi. Jaskowski, inspired by a question of Lukasiewicz in 1926, reports in his [30] that he answered the question by putting the “method of an arbitrary supposition” under the “form of structural rules” and settling the relation to the standard “theory of deduction”, i.e., proving the equivalence of his calculus with a standard axiomatic one. For another, complementary perspective, see [38, 39] and [21].

  18. Jaskowski claims in a footnote of (Jaśkowski [30], p. 7) that he had used boxes in 1926 to articulate his method of supposition. He gives in that very footnote, as an example, the proof we will construct next.

  19. The use of the \(\perp \) symbol is discussed in Appendix 1. Let us mention here that \(\perp \) is used only in proofs to note that a pair of contradictory formulae is to be proved. As we are searching for normal proofs, the choice of contradictory pairs can be restricted to those that have as their “negative” part a formula that has a positive occurrence in an assumption or premise (on which the line with \(\perp \) depends).

  20. Here is the German text: Beim wirklichen Schliessen überspringt man oft eine Reihe von Schlüssen, die durch lange Gewohnheit selbstverständlich geworden sind. Dies soll bei der folgenden Formalisierung nicht nachgemacht werden, sondern jeder Schritt eines ”Beweises” soll einzeln wiedergegeben werden, da es darauf ankommt, die Grundbestandteile des logischen Schliessens aufzudecken.

  21. In AProS there are generic introduction and elimination rules for definitions, \(\mathtt {Def}\)-\(\mathtt {I}\) and \(\mathtt {Def}\)-\(\mathtt {E}\). These generic rules use the correct definition automatically.

  22. At the end of his [33], Mac Lane emphasized: “There remains the real question of the actual structure of mathematical proofs and their strategy. It is a topic long given up by mathematical logicians, but one which still—properly handled—might give us some real insight.” (p. 66)—Mac Lane expressed the very radical aspirations of the thesis in letters to his mother, written when working on the thesis; for example, on April 20, 1933, he asserted: “Perhaps I have time to tell you about my new discovery. It is a new symbolic logic for mathematical proof. It applies, as far as I can see, to all proofs in all branches of mathematics (a rather large order). It makes it possible to write down the proof of a theorem in a very much shorter space than the usual method and at the same time it makes the proof of the theorem much clearer. In essence, it eliminates practically all the long mechanical operations necessary to prove a theorem. It is only necessary to give in sequence the leading ideas of the proof. In fact, once these leading ideas are given—together with a few directions—then it becomes possible to compute from the leading ideas just what the proof of the theorem will be. In other words, once the leading ideas are given, all the rest is a purely mechanical sort of job.” (Mac Lane [34], pp. 60–61)

  23. The analysis of the mathematical frame for the proof of the Pythagorean theorem in Book I and the analogy to the proof of the Cantor–Bernstein Theorem are both found in [48], Sect. 4 that is entitled Local Axiomatics.

  24. We follow G&G and do not include sequences of variables in the definition of boxes. They assert, “we suppress the variables as they tend to clutter the exposition” (l.c., p. 268). For us there is also a second reason. These variables are involved in choosing instantiations of existentially quantified statements; that problem is addressed by AProS in a quite different way. It is discussed below.

  25. G&G introduce in this context a more general concept of “formula corresponding to a box”; that can be defined easily by recursion on the very concept of box and target: if a target is a list of boxes then the formulae associated with them are joined into a disjunction.

  26. Our remark conflicts, of course, with G&G’s rather dismissive observation on page 262, where they distinguish sharply between their “sequents” and the ordinary sequents of, well, of Gentzen’s sequent calculi: only one formula as a succedent or consequent. They write: “Consequents [interpreted disjunctively] may be more attractive from a logical point of view for symmetry reasons, but the convention we adopt ...is in our judgment closer to how humans would think of ‘the current state of play’ when they are in the middle of solving a problem, and that is more important to us than logical neatness.” This remark is only applicable to the sequent calculus for classical logic; in the case of intuitionist logic the consequent is either empty or consists of one formula. As G&G treat only intuitionist logic, the difference in the basic form does not matter at all. It is the completely different “meaning” of the sequents that is significant here; see Appendix 2.

  27. There are two additional tactics that allow the deletion of assumptions, namely, deleteDangling and deleteUnmatchable; the assumptions to be deleted have been previously used and “ have no obvious use”, (l.c., p. 272). The general purpose of these tactics is described in G&G’s section 3.3 on pp. 264–265 and will be discussed below.

  28. Much more could be said about the use of these rules through deep extraction using an extended subformula property when the definiens is viewed as the “subformula” of the definiendum. If a disjunction or an existentially quantified is discovered as a positive subformula, conversion or division might be triggered.

  29. In [3], the role of the Mizar mathematical library in interactive theorem proving is described in great detail and with a good deal of overlap. The general spirit we expressed for the mathematical frame is expressed then for the Mizar mathematical library (on p. 23), namely, that it “was considered an experiment of practical formal modeling of mathematics.”

  30. Logic&Proofs has been offered as a fully web-based course, in various stages of development, since 2007. It has been successfully completed by more than 12000 students at many different institutions. For more information, see AProS Site (http://www.phil.cmu.edu/projects/apros/) and Logic&Proofs Course(https://oli.cmu.edu/courses/logic-proofs-copy/).

References

  1. Andrews, P.B.: Transforming matings into natural deduction proofs. In: Bibel, W., Kowalski, R., (eds.) 5-th Conference on Automated Deduction, Lecture Notes in Computer Science, pp. 281–292. Springer (1980)

  2. Andrews, P.B.: More on the problem of finding a mapping between clause representation and natural-deduction representation. J. Autom. Reason. 7(2), 285–286 (1991)

    Article  Google Scholar 

  3. Bancerek, G., Byliński, C., Grabowski, A., Korniłowicz, A., Matuszewski, R., Naumowicz, A., Pak, K.: The role of the Mizar mathematical library for interactive proof development in Mizar. J. Autom. Reason. 61(1–4), 9–32 (2018)

    Article  MathSciNet  Google Scholar 

  4. Bernays, P.: Beiträge zur axiomatischen Behandlung des Logik-Kalküls. Georg-August-Universität Göttingen, Habilitation (1918)

    Google Scholar 

  5. Bledsoe, W.: Non-resolution theorem proving. Artif. Intell. 9(1), 1–35 (1977)

    Article  MathSciNet  Google Scholar 

  6. Bledsoe, W.: The UT natural deduction prover. Technical Report, Department of Computer Science, University of Texas at Austin (1983)

  7. Byrne, O.: The First Six Books of the Elements of Euclid. Pickering, London (1847)

    Google Scholar 

  8. Byrnes, J.: Proof search and normal forms in natural deduction. PhD thesis, Carnegie Mellon University (1999)

  9. Church, A.: An unsolvable problem of elementary number theory. Am. J. Math. 58(2), 345–363 (1936)

    Article  MathSciNet  Google Scholar 

  10. Cittadini, S.: Intercalation calculus for intuitionistic propositional logic. Technical Report PHIL-29, Philosophy, Methodology, and Logic, Carnegie Mellon University (1992)

  11. Diaz Lopez, A.: Sir Timothy Gowers interview. Not. Am. Math. Soc. 63(9), 1026–1028 (2016)

    Article  MathSciNet  Google Scholar 

  12. Fitch, F.B.: Symbolic Logic: An Introduction. Ronald Press, New York (1952)

    MATH  Google Scholar 

  13. Fitting, M.: First-Order Logic and Automated Theorem Proving. Springer, Berlin (1990)

    Book  Google Scholar 

  14. Ganesalingam, M., Gowers, W.T.: A fully automatic problem solver with human-style output. arXiv:1309.4501 (2013)

  15. Ganesalingam, M., Gowers, W.T.: A fully automatic theorem prover with human-style output. J. Autom. Reason. 58(2), 253–291 (2017)

    Article  MathSciNet  Google Scholar 

  16. Gentzen, G.: Urdissertation, Wissenschaftshistorische Sammlung, Eidgenössische Technische Hochschule. Zürich, Bernays Nachlass, Ms ULS (A detailed description of the manuscript is found in (von Plato 2009) (1932-3)

  17. Gentzen, G.: Untersuchungen über das logische Schließen I, II. Mathematische Zeitschrift 39(1):176–210, 405–431 (1934-5)

  18. Gentzen, G.: Die Widerspruchsfreiheit der reinen Zahlentheorie. Mathematische Annalen 112(1), 493–565 (1936)

    Article  MathSciNet  Google Scholar 

  19. Gentzen, G.: Neue Fassung des Widerspruchsfreiheitsbeweises für die reine Zahlentheorie. Forschung zur Logik und zur Grundlegung der exakten Wissenschaften. Neue Folge 4, S Hirzel:19–44 (1938)

  20. Harrison, J., Urban, J., Wiedijk, F.: History of interactive theorem proving. Comput. Logic 9, 133–214 (2014)

    MathSciNet  MATH  Google Scholar 

  21. Hazen, A.P., Pelletier, F.J.: Gentzen and Jaśkowski on natural deduction: Fundamentally similar but importantly different. Stud. Logica. 102(6), 1103–1142 (2014)

    Article  Google Scholar 

  22. Heule, M.J., Kullmann, O.: The science of brute force. Commun. ACM 60(8), 70–79 (2017)

    Article  Google Scholar 

  23. Hilbert, D.: Grundlagen der Geometrie. Teubner, Stuttgart (1899)

    MATH  Google Scholar 

  24. Hilbert, D.: Axiomatisches Denken. Mathematische Annalen 78:405–415, this paper is translated in: From Kant to Hilbert, W.B. Ewald, editor, Oxford University Press 1996, 1107–1115 (1918)

  25. Hilbert, D.: Die Grundlagen der Mathematik. Abhandlungen aus dem mathematischen Seminar der Hamburgischen Universität (6):65–85 (1927)

  26. Hilbert, D., Bernays, P.: Prinzipien der Mathematik. In: Ewald, W.B., Sieg, W. (eds.) David Hilbert’s Lectures on the Foundations of Arithmetic and Logic 1917–1933, pp. 64–214 . Springer (2013) (1917–1918)

  27. Hilbert, D., Bernays, P.: Grundlagen der Mathematik. In: Ewald, W.B., Sieg, W. (eds) David Hilbert’s Lectures on the Foundations of Arithmetic and Logic 1917–1933, pp. 431–518. Springer (2013) (1921–1922)

  28. Hilbert, D., Bernays, P.: Grundlagen der Mathematik, vol. I. Springer, Berlin (1934)

    MATH  Google Scholar 

  29. Hilbert, D., Bernays, P.: Grundlagen der Mathematik, vol. II. Springer, Berlin (1939)

    MATH  Google Scholar 

  30. Jaśkowski, S.: On the rules of suppositions in formal logic. Stud. Logica. 1, 5–32 (1934)

    MATH  Google Scholar 

  31. Mac Lane, S.: Abgekürzte Beweise im Logikkalkul [sic]. Dissertation, Georg-August-Universität Göttingen (1934)

  32. Mac Lane, S.: A logical analysis of mathematical structure. The Monist 45(1), 118–130 (1935)

    Article  Google Scholar 

  33. Mac Lane, S.: A late return to a thesis in logic. In: Kaplansky, I. (ed) Saunders Mac Lane-Selected Papers, pp. 63–66. Springer (1979)

  34. Mac Lane, S.: Saunders Mac Lane: A Mathematical Autobiography. A.K, Peters (2005)

    Book  Google Scholar 

  35. Mac Kenzie, D.: The automation of proof: a historical and sociological exploration. IEEE Ann. Hist. Comput. 17(3), 7–29 (1995)

    Article  MathSciNet  Google Scholar 

  36. Newell, A., Simon, H.A.: The logic theory machine a complex information processing system. Technical report, (No .P-868) The Rand Corporation (1956)

  37. Pelletier, F.J.: Automated natural deduction in THINKER. Stud. Logica 60(1), 3–43 (1998)

    Article  MathSciNet  Google Scholar 

  38. Pelletier, F.J.: A brief history of natural deduction. Hist. Philos. Logic 20(1), 1–31 (1999)

    Article  MathSciNet  Google Scholar 

  39. Pelletier, F.J., Hazen, A.P.: A history of natural deduction. In: Gabbay, D., Pelletier, F.J., Woods, J. (eds.) Handbook of the History of Logic, vol. 11, pp. 341–414. Elsevier, London (2012)

    Google Scholar 

  40. Pfenning, F.: Proof transformations in higher-order logic. PhD thesis, Carnegie Mellon University (1987)

  41. Pfenning, F., Sieg, W. (eds): Natural deduction. Special Issue of Studia Logica 60 (1998)

  42. Pollock, J.: Skolemization and unification in natural deduction. unpublished paper available at http://www.uarizonaedu/~pollock (1997)

  43. Prawitz, D.: Natural Deduction—A Proof-Theoretical Study. Almqvist & Wiksell, Stockholm (1965)

    MATH  Google Scholar 

  44. Rips, L.J.: The Psychology of Proof—Deductive Reasoning in Human Thinking. MIT Press, London (1994)

    Book  Google Scholar 

  45. Sieg, W.: Mechanisms and Search—Aspects of Proof Theory, vol. 14. Associazione Italiana di Logica e sue Applicazioni (1992)

  46. Sieg, W.: The AProS project: Strategic thinking and computational logic. Logic J. IGPL 15(4), 359–368 (2007)

    Article  Google Scholar 

  47. Sieg, W.: Review of (von Plato 2008). Mathematical Reviews 2413304 (2009)

  48. Sieg, W.: Searching for proofs (and uncovering capacities of the mathematical mind). In: Feferman, S., Sieg, W. (eds.) Proof, Categories and Computations, pp. 189–215. College Publications, New York (2010)

    MATH  Google Scholar 

  49. Sieg, W., Byrnes, J.: Normal natural deduction proofs (in classical logic). Stud. Logica 60(1), 67–106 (1998)

    Article  MathSciNet  Google Scholar 

  50. Sieg, W., Cittadini, S.: Normal natural deduction proofs (in non-classical logics). In: Mechanizing Mathematical Reasoning. Lecture Notes in Computer Science 2605, pp. 169–191. Springer (2005)

  51. Sieg, W., Field, C.: Automated search for Gödel’s proofs. Ann. Pure Appl. Logic 133, 319–338 (2005)

  52. Sieg, W., Scheines, R.: Searching for proofs (in sentential logic). In: Burkholder, L. (ed.) Philosophy and the Computer, pp. 137–159. Westview Press, Nashville (1992)

    Google Scholar 

  53. Sieg, W., Walsh, P.: Natural formalization: Deriving the Cantor–Bernstein theorem in ZF. Rev. Symb. Logic 1–35 (2019)

  54. Stefferud, E.: The logic theory machine: A model heuristic program (Memorandum No. RM-3731-CC). The Rand Corporation (1963)

  55. Thiele, R.: Hilbert’s twenty-fourth problem. Am. Math. Mon. 110(1), 1–24 (2003)

  56. Troelstra, A.S., Schwichtenberg, H.: Basic Proof Theory, vol. 43. Cambridge University Press, Cambridge (2000)

    Book  Google Scholar 

  57. Turing, A.M.: On computable numbers, with an application to the Entscheidungsproblem. Proc. Lond. Math Soc. 42, 230–265 (1936)

    MathSciNet  MATH  Google Scholar 

  58. Von Plato, J.: Gentzen’s proof of normalization for natural deduction. Bull. Symb. Logic 14(2), 240–257 (2008)

  59. Wang, H.: Toward mechanical mathematics. IBM J. Res. Dev. 4(1), 2–22 (1960)

    Article  MathSciNet  Google Scholar 

  60. Wos, L.: The problem of finding a mapping between clause representation and natural-deduction representation. J. Autom. Reason. 6(2), 211–212 (1990)

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Philosophy, Carnegie Mellon University, Pittsburgh, USA

    Wilfried Sieg & Farzaneh Derakhshan

Authors
  1. Wilfried Sieg
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Farzaneh Derakhshan
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Wilfried Sieg.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendices

Appendix 1

Here are the rules of the NI calculus. We present first the elimination rules; they are to be read “upward” as one is taking a “gap-closing” or intercalating step. This continues the description of the NI calculus from toward the end of Sect. 1; in particular, we do not repeat the role of extraction sequences for the elimination rules.

figure aj

The I-rules for these connectives are the usual ones; see (Gentzen [17], p. 186) or (Prawitz [43], p. 20). The rules for \(\perp \) and negation are formulated next.

figure ak

This is, without \(\lnot E\), “exactly” the formulation for intuitionist logic given in (Gentzen [17], p. 186). Unfortunately, Gentzen called \(\bot I\), “Negationsbeseitigung” and expanded this calculus to its classical form by adding, for example, the law of the excluded middle \(\phi \vee \lnot \phi \) or the rule of double negation elimination. Dropping \(\bot \,E\) leads to minimal logic.

Appendix 2

We discussed most of the tactics used by the G&G-prover already in Sect. 3. Let us look here at a few more examples on how tactics can be mimicked by rules of the NI calculus, i.e., can be viewed as derived rules.

A Tidying Tactic: peelAndSplitUniversalonditionalTarget

figure al

An Applying Tactic:

  • expandPreExistentialHypothesis.

    Let \(\chi \) be by definition \((\exists x) \phi (x)\);

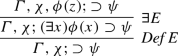
  • backwardsLibraryReasoning.

    Let \((\forall u) (P(u) \rightarrow Q(u))\) be a lemma; this is reflected by backward reasoning in our setting using the lemma as a rule:

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Sieg, W., Derakhshan, F. Human-Centered Automated Proof Search. J Autom Reasoning 65, 1153–1190 (2021). https://doi.org/10.1007/s10817-021-09594-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10817-021-09594-z

Keywords

Search

Navigation