Linear semi-supervised projection clustering by transferred centroid regularization

Abstract

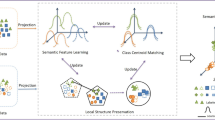
We propose a novel method, called Semi-supervised Projection Clustering in Transfer Learning (SPCTL), where multiple source domains and one target domain are assumed. Traditional semi-supervised projection clustering methods hold the assumption that the data and pairwise constraints are all drawn from the same domain. However, many related data sets with different distributions are available in real applications. The traditional methods thus can not be directly extended to such a scenario. One major challenging issue is how to exploit constraint knowledge from multiple source domains and transfer it to the target domain where all the data are unlabeled. To handle this difficulty, we are motivated to construct a common subspace where the difference in distributions among domains can be reduced. We also invent a transferred centroid regularization, which acts as a bridge to transfer the constraint knowledge to the target domain, to formulate this geometric structure formed by the centroids from different domains. Extensive experiments on both synthetic and benchmark data sets show the effectiveness of our method.

Appendix

Definition 1

(Lee and Seung 2001) Z(h,h′) is an auxiliary function for F(h) if the conditions

$$ \begin{array}{rll} Z(h,{h^{\prime}}) &\ge& F(h) \\ Z(h,h) &=& F(h) \end{array} $$

are satisfied.

Lemma 1

(Lee and Seung 2001) If Z is an auxiliary function for F , then F is non-increasing under the update

$$ {h^{(t + 1)}} = \arg \mathop { \min }\limits_h Z(h,{h^{(t)}}) $$

Proof

By construction, we have F(h ^(t + 1)) ≤ Z(h ^(t + 1),h ^t) ≤ Z(h ^t,h ^t) = F(h ^(t)). Thus, F(h ^(t)) is monotone decreasing.□

We write objective function (19) as

$$ \begin{array}{rll} F_{\mathbf{H}} &=& \textrm{tr}(\mathbf{H}^T \mathbf{A}\mathbf{H}) \\ &\rm{s.t.}& \mathbf{H} \ge 0 \end{array} $$

(28)

where H = L _s . From Lemma 1, in order to prove objective function (28) to be a non-increasing function, we need to construct an appropriate Z(h ^(t + 1),h ^t) and derive its global minimum.

Lemma 2

Given the objective function (28) where all elements in H are nonnegative, the following function

$$ Z(\mathbf{H}, \mathbf{H}^{\prime}) = \sum\limits_{ik} {\frac{{{{({\mathbf{A}}^{+}{{\mathbf{H}}^{\prime}})}_{ik}}{\mathbf{H}}_{ik}^2}}{{{\mathbf{H}}^{\prime}_{ik}}}} - \sum\limits_{ikl} {{{\mathbf{A}}^{-}_{il} }\mathbf{H}^{\prime}_{lk} \mathbf{H}^{\prime}_{ik} \left(1 + \log \frac{{{\mathbf{H}_{lk}}} {{\mathbf{H}_{ik}}} }{{{\mathbf{H}^{\prime}_{lk}}} {\mathbf{H}^{\prime}_{ik}} }\right)} $$

(29)

is an auxiliary function for F _H . Furthermore, it is a convex function in H and its global minimum is

$$ \mathbf{H}_{ij} = \mathbf{H}^{\prime}_{ij} \sqrt {\frac{{\left[{\bf{A}}^{-}\mathbf{H}^{\prime}\right]_{ij} }}{{\left[{\bf{A}}^{+}\mathbf{H}^{\prime} \right]_{ij} }}} $$

(30)

Proof

We rewrite (28) as

$$ F_\mathbf{H} = \textrm{tr}(\mathbf{H}^T \mathbf{A}^{+}\mathbf{H} - \mathbf{H}^T \mathbf{A}^{-}\mathbf{H}) $$

We find an upper bound for the first term and an lower bound for the second term. Using Lemma 3 (see below) and setting D ←I, C ←A ⁺, we obtain an upper bound

$$ \textrm{tr}(\mathbf{H}^T \mathbf{A}^{+}\mathbf{H}) \le \sum\limits_{i = 1}^n {\sum\limits_{k = 1}^p {\frac{{{{({\mathbf{A}}^{+}{{\mathbf{H}}^{\prime}})}_{ik}}{\mathbf{H}}_{ik}^2}}{{{\mathbf{H}}^{\prime}_{ik}}}} } $$

To obtain the lower bound for the second term, we use inequality z ≥ 1 + logz, which holds for any z > 0, and derive

$$ \frac{{{\mathbf{H}_{lk}}} {{\mathbf{H}_{ik}}} }{{\mathbf{H}^{\prime}_{lk}} {\mathbf{H}^{\prime}_{ik}}} \ge 1 + \log \frac{{{\mathbf{H}_{lk}}} {{\mathbf{H}_{ik}}} }{{{\mathbf{H}^{\prime}_{lk}}} {\mathbf{H}^{\prime}_{ik}} } $$

(31)

From (31), the second term is bounded by

$$ \textrm{tr}(\mathbf{H}^T \mathbf{A}^{-}\mathbf{H}) \ge \sum\limits_{ikl} {{{\mathbf{A}}^{-}_{il} }\mathbf{H}^{\prime}_{lk} \mathbf{H}^{\prime}_{ik} \left(1 + \log \frac{{{\mathbf{H}_{lk}}} {{\mathbf{H}_{ik}}} }{{{\mathbf{H}^{\prime}_{lk}}} {\mathbf{H}^{\prime}_{ik}} }\right)} $$

(32)

Collecting two bounds, we obtain Z(H, H′) as shown in (29). It is obvious that F _H  ≤ Z(H, H′) and F _H  ≤ Z(H, H) . To find the minimum of Z(H, H′), we take

$$ \frac{{\partial Z(\mathbf{H}, \mathbf{H}^{\prime})}}{{\partial \mathbf{H}_{ik}}} = \frac{2(\mathbf{A}^{+}\mathbf{H}^{\prime})_{ik} \mathbf{H}_{ik}}{\mathbf{H}^{\prime}_{ik}} - \frac{2(\mathbf{A}^{-}\mathbf{H}^{\prime})_{ik} \mathbf{H}^{\prime}_{ik}}{\mathbf{H}_{ik}} $$

(33)

The Hessian matrix of Z(H, H′), which contains the second derivatives,

$$ \frac{{\partial^2 Z(\mathbf{H}, \mathbf{H}^{\prime})}}{{\partial \mathbf{H}_{ik}}{\partial \mathbf{H}_{jl}}} = \delta_{ij} \delta_{kl}\left( \frac{2(\mathbf{A}^{-} \mathbf{H}^{\prime})_{ik} \mathbf{H}^{\prime}_{ik}}{\mathbf{H}^{2}_{ik}} + \frac{2(\mathbf{A}^{+} \mathbf{H}^{\prime})_{ik} }{\mathbf{H}^{\prime}_{ik}} \right) $$

(34)

is a diagonal matrix with positive entries. Therefore, Z(H, H′) is a convex function of H. We then obtain the global minimum by setting $\frac{{\partial Z(\mathbf{H}, \mathbf{H}^{\prime})}}{{\partial \mathbf{H}_{ik}}} = 0$ and solving for H, from which we can get (23).□

Lemma 3

(Ding et al. 2010) For any nonnegative matrix C ∈ ℝ^{n ×n} , D ∈ ℝ^{p ×p} , S ∈ ℝ^{n ×p} , S′ ∈ ℝ^{n ×k} , and C , D are symmetric, the following inequality holds.

$$ \sum\limits_{i = 1}^n {\sum\limits_{k = 1}^p {\frac{{{{({\mathbf{C}}{{\mathbf{S}}^{\prime}}{\mathbf{D}})}_{ik}}{\mathbf{S}}_{ik}^2}}{{{\mathbf{S}}^{\prime}_{ik}}}} } \ge tr({{\mathbf{S}}^T}{\mathbf{CSD}}) $$