Dynamic pricing for non-instantaneous deteriorating items

Abstract

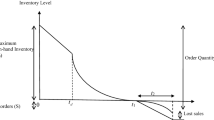
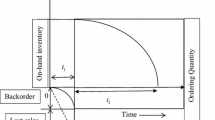
An optimal dynamic pricing strategy for non-instantaneous deteriorating items exhausted in a sales period without replenishment is explicitly characterized. Originally, the inventory level of the items reduces simply as a result of customer demand, and subsequently decreases owing to both demand and deterioration. This paper formulates a dynamic pricing model to maximize the enterprise’s profit. The optimal dynamic pricing strategy is obtained by solving the optimization problem based on Pontryagin’s maximum principle. Two static pricing models, including a uniform pricing model and a two-stage pricing model, are carried out to compare with the dynamic pricing model to show the significant advantage of the dynamic strategy. Furthermore, numerical examples, together with sensitivity analysis of the optimal solution with respect to major parameters, are provided to illustrate the effectiveness of the proposed method.

Appendix

Proof

As for Case 1, if $\lambda (0)\ge -\frac{\alpha }{\beta }$, which yields $h\le \frac{\alpha \theta }{\beta }\frac{1+{e}^{\theta (t_{d}-T)}}{1-{e}^{\theta (t_{d}-T)}+\theta t_{d}}$ known from (11), the optimal pricing strategy is shown as

$$\begin{aligned} \begin{array}{ll} P^{*}(t)=\left\{ \begin{array}{ll} \displaystyle \frac{1}{2}\left( h(t{-}t_{d}){+}M{e}^{\theta (t_{d}-T)}+N\right) ,&{}\quad 0\le t\le t_{d}\\ \displaystyle \frac{1}{2}\left( M{e}^{\theta (t-T)}+N\right) ,&{}\quad t_{d}<t\le T.\\ \end{array}\right. \end{array}\nonumber \\ \end{aligned}$$

(35)

Substituting (35) into (1), one can obtain the inventory with $I(0)=I_{0}$ as

$$\begin{aligned}&I^{*}(t)=\nonumber \\&\quad \left\{ \begin{array}{ll} \displaystyle \frac{h\beta t^{2}}{4}+\frac{\beta M}{2}\left( {e}^{\theta (t_{d}-T)}-1\right) t-\frac{h\beta t_{d}}{2}t+I_{0}, &{}\quad 0\le t\le t_{d}\\ \displaystyle \frac{\beta M}{4\theta }{e}^{\theta (t-T)}-\displaystyle \frac{\beta M}{2\theta }{+}C_{11}{e}^{-\theta t},&{}\quad t_{d}<t\le T,\\ \end{array}\right. \end{aligned}$$

(36)

where

$$\begin{aligned} C_{11}&= {e}^{\theta t_{d}}\left( I_{0}-\frac{h\beta t_{d}^{2}}{4}+\frac{\beta M}{2}\left( \frac{1}{\theta }-t_{d}\right) \right. \\&\quad \left. +\frac{\beta M}{2}\left( t_{d}-\frac{1}{2\theta }\right) {e}^{\theta (t_{d}-T)}\right) . \end{aligned}$$

To satisfy $I(T)=0, T$ should meet the condition shown in (16).

As for Case 2, if $\lambda (t_{d})\ge -\frac{\alpha }{\beta }$ and $\lambda (0)<-\frac{\alpha }{\beta }$, which yield $\frac{\alpha \theta }{\beta }\frac{1+{e}^{\theta (t_{d}-T)}}{1-{e}^{\theta (t_{d}-T)}+\theta t_{d}}<h\le \frac{\alpha \theta }{\beta }\frac{1+{e}^{\theta (t_{d}-T)}}{1-{e}^{\theta (t_{d}-T)}}$ known from (11), the optimal pricing strategy is shown as

$$\begin{aligned} P^{*}(t)=\left\{ \begin{array}{ll} 0,&{}\quad 0{\le } t\le t_{1}\\ \displaystyle \frac{1}{2}\left( h(t{-}t_{d}){+}M{e}^{\theta (t_{d}-T)}{+}N\right) ,&{}\quad t_{1}<t\le t_{d}\\ \displaystyle \frac{1}{2}\left( M{e}^{\theta (t{-}T)}{+}N\right) ,&{}\quad t_{d}<t\le T,\\ \end{array}\right. \nonumber \\ \end{aligned}$$

(37)

where $t_{1}=t_{d}-\displaystyle \frac{1}{h}\left( N+M{e}^{\theta (t_{d}-T)}\right)$ derived from $\lambda (t_{1})=-\displaystyle \frac{\alpha }{\beta }$.

By virtue of (1), (37) and $I(0)=I_{0}$, the inventory is given by

$$\begin{aligned} I^{*}(t)=\left\{ \begin{array}{ll} -\alpha t+I_{0},&{}\quad 0\le t\le t_{1}\\ \displaystyle \frac{h\beta t^{2}}{4}+\frac{\beta M}{2}\left( {e}^{\theta (t_{d}-T)}-1\right) t&{}\\ \quad -\frac{h\beta t_{d}}{2}t+C_{21}, &{}\quad t_{1}<t\le t_{d}\\ \displaystyle \frac{\beta M}{4\theta }{e}^{\theta (t-T)}-\frac{\beta M}{2\theta }+C_{22}{e}^{-\theta t}, &{}\quad t_{d}<t\le T, \end{array}\right. \nonumber \\ \end{aligned}$$

(38)

where

$$\begin{aligned} C_{21}&= I_{0}-\alpha t_{d}+\frac{h\beta t_{d}^{2}}{4}+\frac{\beta N^{2}}{4h}+\frac{\beta M t_{d}}{2}\\&\quad +\frac{\beta M}{2}\left( \frac{N}{h}-t_{d}\right) {e}^{\theta (t_{d}-T)}+\frac{\beta M^{2}}{4h}{{e}}^{2\theta (t_{d}-T)}, \end{aligned}$$

and

$$\begin{aligned} C_{22}&= \left( I_{0}-\alpha t_{d}+\frac{\beta M}{2\theta }+\frac{\beta N^{2}}{4h}+\frac{\beta M^{2}}{4h}{e}^{2\theta (t_{d}-T)}\right. \\&\quad \left. +\frac{\beta M}{2}\left( \frac{N}{h}-\frac{1}{2\theta }\right) {e}^{\theta (t_{d}-T)}\right) {{e}}^{\theta t_{d}}. \end{aligned}$$

With $I_{2}(T)=0, T$ should satisfy Eq. (18).

As for Case 3, if $\lambda (t_{d})<-\frac{\alpha }{\beta }$, which yields $h>\frac{\alpha \theta }{\beta }\frac{1+{e}^{\theta (t_{d}-T)}}{1-{e}^{\theta (t_{d}-T)}}$ known from (11), the optimal pricing strategy is shown as

$$\begin{aligned} \begin{array}{ll} P^{*}(t)=\left\{ \begin{array}{ll} 0,&{}\quad 0\le t\le t_{2}\\ \displaystyle \frac{1}{2}\left( M{e}^{\theta (t-T)}+N\right) ,&{}\quad t_{2}<t\le T,\\ \end{array}\right. \end{array} \end{aligned}$$

(39)

where $t_{2}=T+\frac{1}{\theta }\ln (-\frac{N}{M})$ derives from $\lambda (t_{2})=-\frac{\alpha }{\beta }$.

According to (1) and $I(0)=I_{0}$, the inventory is given by

$$\begin{aligned} I^{*}(t)=\left\{ \begin{array}{ll} -\alpha t+I_{0},&{}\quad 0\le t\le t_{d}\\ \displaystyle \frac{1}{\theta }\left( C_{31}{e}^{-\theta t}-\alpha \right) ,&{} \quad t_{d}<t\le t_{2}\\ \displaystyle \frac{\beta M}{4\theta }{e}^{\theta (t-T)}-\frac{\beta M}{2\theta }+C_{32}{e}^{-\theta t}, &{}\quad t_{2}<t\le T, \end{array}\right. \nonumber \\ \end{aligned}$$

(40)

where

$$\begin{aligned} C_{31}={e}^{\theta t_{d}}(\theta I_{0}-\alpha \theta t_{d}+\alpha ), \end{aligned}$$

and

$$\begin{aligned} C_{32}=\left( I_{0}-\alpha t_{d}+\frac{\alpha }{\theta }\right) {e}^{\theta t_{d}}+\frac{\beta N^{2}}{4M\theta }{e}^{\theta T}. \end{aligned}$$

To satisfy $I(T)=0, T$ should meet the condition shown in (20).

As for Case 4, if $\lambda (0)\ge -\frac{\alpha }{\beta }$, which is equivalent to $h\le \frac{2\alpha }{\beta T}$ known from (15), the pricing strategy is shown as

$$\begin{aligned} P^{*}(t)=\displaystyle \frac{1}{2}h(t-T)+\frac{\alpha }{\beta },\quad 0\le t\le T. \end{aligned}$$

(41)

With $I(0)=I_{0}$, the inventory is consequently given by

$$\begin{aligned} I^{*}(t)=\frac{h\beta }{4}t^{2}-\frac{h\beta T}{2}t+I_{0}, \quad 0\le t\le T. \end{aligned}$$

(42)

Note that $I(T)=0. T$ should meet the condition shown in (22), making $h\le \frac{2\alpha }{\beta T}$, i.e., $h\le \frac{\alpha ^{2}}{\beta I_{0}}$.

As for Case 5, if $\lambda (0)<-\frac{\alpha }{\beta }$, which yields $h>\frac{2\alpha }{\beta T}$ known from (15), the pricing strategy is shown as

$$\begin{aligned} P^{*}(t)=\left\{ \begin{array}{l@{\quad }l} 0,&{} 0\le t\le t_{3}\\ \displaystyle \frac{1}{2}h(t-T)+\frac{\alpha }{\beta },\quad &{}t_{3}<t\le T,\\ \end{array}\right. \end{aligned}$$

(43)

where $t_{3}=T-\displaystyle \frac{2\alpha }{h\beta }$.

Considered $I(0)=I_{0}$, it follows that

$$\begin{aligned} I^{*}(t)=\left\{ \begin{array}{ll} -\alpha t+I_{0},&{} 0\le t\le t_{3}\\ \displaystyle \frac{h\beta }{4}t^{2}-\frac{h\beta T}{2}t+I_{0}-\alpha T&{}\\ \quad +\frac{\alpha ^{2}}{h\beta }+\frac{h\beta }{4}T^{2}, &{}t_{3}<t\le T. \end{array}\right. \end{aligned}$$

(44)

Further, to satisfy $I(T)=0, T$ should meet the condition shown in (24), making $h>\frac{2\alpha }{\beta T}$, i.e., $h>\frac{\alpha ^{2}}{\beta I_{0}}$. The proof is complete.