A heuristic master planning algorithm for recycling supply chain management

Abstract

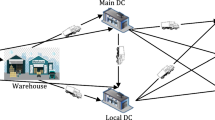
This study focuses on solving a multi-objective master planning (MP) problem for a recycling supply chain, including collectors, disassemblers, shredders, reconditioners and garbage handlers. An MP problem for a recycling supply chain is solved to determine the optimal transporting and processing operations, while considering multiple product structures, multiple discrete planning periods, and multiple demands, stocking and garbage handling quantities. To solve the MP problem, we propose a multiple-goal mixed integer programming model with two objectives: minimize the total delay cost and minimize the sum of processing cost, transportation cost, holding cost, setup cost and garbage handling cost. To improve the effectiveness and efficiency of the solution process, we propose a heuristic algorithm, RPMPA, which consists of three phases: preliminary works, demand grouping and sorting algorithm, and the Recycling Process Path Selection Algorithm. We built a prototype based on RPMPA, and constructed a scenario analysis to show the effectiveness and efficiency of RPMPA.

Appendix

The following indices and parameters were defined prior to constructing the MIP model.

Indices: $h, i$, and $j$ are nodes where $h, i, j = 1, 2, {\ldots }, {\vert }V{\vert }$ given $V$ is the set of nodes in a recycling supply chain network; $r$ represents demands where $r = 1, 2,{\ldots }, d;\, t$ is the time bucket where $t = 1, 2,{\ldots }, T$; and $m$ and $n$ are items or materials where $m,\, n = 1, 2,{\ldots },{\vert }M{\vert }$ given $M$ is the set of items and materials that flow within the recycling supply chain.

Parameters:

$V$::

Set of nodes in a recycling supply chain network.

$V$’::

Set of nodes in $V$ except for the Start (source) and End (destination) nodes.

$V^{W}$::

Set of nodes where $W$ representing $C$: collector, $D$: disassembler, $S$: shredder, $R$: reconditioner, and $G$: garbage handling nodes.

$L$::

Set of links in the network.

$DL$::

Set of internal links between disassembler nodes.

$M$::

Set of items and materials that flow within the recycling supply chain.

$P$::

Set of recycled items and materials that are in demand which is the subset of $M$.

$Q$::

Set of returned goods that are collected from consumers which is the subset of $M$.

$DUE_{rm}$::

Due date (in time buckets) for item or material $m$ of demand $r$ where $1\le r \le d$ and $m\in P$.

$DEM_{rm}$::

Demand quantity for item or material $m$ of demand $r$ where $1\le r \le d$ and $m \in P$.

$DC_{rm}$::

Unit delay penalty per unit time bucket for item or material $m$ of demand $r$ where $1\le r \le d$ and $m\in P$.

$Demand(t)$::

Set of demands with due date $t$ where $1\le t \le T$.

$Parent(n)$::

Set of parent items of $n$ where $n \in M$.

$RUSE_{mn}$::

Quantity of recycled items $n$ reprocessed from item $m$ per unit where $m \in Parent(n)$ and $n \in M$.

$CX_{it}$::

Capacity limit of node $i$ at time bucket $t$ where $i \in V^{{\prime }}-V^{G}$ and $1\le t \le T$.

$Cx_{im}$::

Capacity needed at node $i$ when processing (decomposing for disassemblers and shredders) one unit of $m$ where $i \in V^{{\prime }}-V^{G}$ and $m \in M$.

$FC_{it}$::

Setup fixed cost for node $i$ at time bucket $t$ where $i\in V^{{\prime }}$ and $1\le t \le T$.

$PC_{im}$::

Unit processing cost for item $m$ at node $i$ where $i \in V^{{\prime }}-V^{G}$ and $m\in M$.

$PCG_{i}$::

Unit processing cost for garbage at node $i$ where $i \in V^{G}$.

$HC_{im}$::

Unit holding cost for item $m$ at node $i$ where $i \in V^{{\prime }}-V^{G}$ and $m\in M$.

$TC_{ijm}$::

Unit cost for shipping item $m$ from node $i$ to node $j$ where $(i, j) \in L - DL$ and $m\in M$, or the unit cost of holding item $m$ from node $i$ to node $j$ where $(i, j) \in DL$ and $m\in M$.

$LT_{ijm}$::

Lead Time (in time buckets) needed to transfer item $m$ through link $(i,\, j)$ where $(i,\, j) \in L$ and $m\in M$.

$Weight(m)$::

Weight of item or material $m$ where $m \in M$.

$Maxwaste^{W}$::

Upper limit of garbage volume generated by $W$ in a time bucket where $W=C$: collector, $D$: disassembler, $S$: shredder, $R$: reconditioner.

Big_M::

A very large positive number.

Decision variables:

$X_{imt}$::

Production quantity of item $m$ processed at node $i$ in time bucket $t$ where $i \in V ^{{\prime }}-V^{G},\, m \in M$, and $1\le t \le T$.

$S_{ijmt}$::

Quantity of item $m$ to be shipped from node $i$ to node $j$ in time bucket $t$ where $(i, j) \in L,\, m \in M$, and $1\le t \le T$.

$I_{imt}$::

Inventory quantity of item $m$ held at node $i$ in time bucket $t$ where $i \in V^{{\prime }}-V^{G},\, m \in M$, and $1\le t \le T$.

$Z_{rmt}$::

Quantity of item $m$ to fill demand $r$ in time bucket $t$ where $1\le r \le d,\, m \in P$, and $1\le t \le T$.

$Y_{it}$::

A binary variable that indicates whether or not node $i$ operates at time bucket $t$ where $i \in V ^{{\prime }}$ and $1\le t \le T$. If yes, $Y_{it} = 1$. Otherwise, $Y_{it} =0$.

Capacity constraints: Constraint (1) represents the process capacity limitations for all recycled materials at all the nodes, except the garbage handling node, in each time bucket. That is, the total number of items processed at node $i$ in time bucket $t$ cannot exceed the capacity of node $i$.

$$\begin{aligned} \sum \limits _{m=1}^M {Cx_{im} \times X_{imt} \le CX_{it} }\quad \forall i\in V^{{\prime }}-V^{G}, 1\le t\le T \end{aligned}$$

(1)

Demand constraints: There are three sets of constraints associated with demand. Constraint (2) ensures the distribution quantities of recycled item $m$ shipped from reconditioners in time bucket $t$ to be equal to the quantity of produced item $m$ that used to fulfill demand $r$ in that time bucket. Constraint (3) ensures that the total quantity produced of recycled item $m$ of fulfilling demand $r$ through the entire planning horizon is satisfied. Constraint (4) enforces the shipment for each demand after its due date (i.e., no early shipment).

$$\begin{aligned}&\sum \limits _{r=1}^d {Z_{rmt} }=\sum \limits _{(h,END)\in L\wedge h\in V^{R}}{S_{h(END)m(t-LT_{h(END)m} )}}\nonumber \\&\qquad \qquad \qquad \,\,\forall m\in P, 1\le t\le T\end{aligned}$$

(2)

$$\begin{aligned}&\sum \limits _{t=1}^T {Z_{rmt} } =DEM_{rm} \quad \forall 1\le r\le d,m\in P\end{aligned}$$

(3)

$$\begin{aligned}&\sum \limits _{t=1}^{DUE_{rm} -1} {Z_{rmt} } =0\quad \forall 1\le r\le d,m\in P \end{aligned}$$

(4)

Inventory constraints: For each node, the inventory of item $m$ at the end of time bucket $t$ is equal to the produced/received quantity plus the inventory in time bucket $t$-1 minus the quantity shipped out/consumed. Corresponding to different types of nodes, there are three sets of constraints. Constraint (5) is the inventory balancing equation for each recycled item at each collector node in each time bucket. Constraints (6) are the inventory balancing equations for each recycled item at each node of disassembler, shredder, and reconditioner in each time bucket. Take a disassembler as an example, closing inventory at time = Opening stock at time + flow in quantity + quantity obtained from decomposing parent items – flow out quantity – quantity used for decomposition. Constraint (7) is the inventory balancing equation for each scrap item at the garbage handling node.

$$\begin{aligned}&I_{im(t-1)} -\sum \limits _{(i,j)\in L} {S_{ijmt} } +X_{imt}\nonumber \\&\quad =I_{imt} \,\forall i\in V^{C},m\in Q, 1\le t\le T\end{aligned}$$

(5)

$$\begin{aligned}&I_{in(t-1)} +\sum \limits _{m\in Parent(n)} {(X_{imt} \times RUSE_{mn} )}\nonumber \\&\quad -\sum \limits _{(i,j)\in L} {S_{ijnt} } -X_{\mathrm{int}} =I_{\mathrm{int}} \end{aligned}$$

(6)

$$\begin{aligned}&\forall i\in V^{D}\cup V^{S}\cup V^{R},n\in M, 1\le t\le LT_{hin} \hbox { and} \nonumber \\&I_{in(t-1)} +\sum \limits _{(h,i)\in L} {S_{hin(t-LT_{hin} )} }\nonumber \\&\quad +\sum \limits _{m\in Parent(n)} {(X_{imt} \times RUSE_{mn} )}\nonumber \\&\quad -\sum \limits _{(i,j)\in L} {S_{ijnt} } -X_{\mathrm{int}} =I_{\mathrm{int}} \nonumber \\&\forall i\in V^{D}\cup V^{S}\cup V^{R},n\in M, LT_{hin} \le t\le T \nonumber \\&\sum \limits _{(h,i)\in L} {S_{him(t-LT_{him} )} }\nonumber \\&\quad =\sum \limits _{(i,END)\in L} {S_{ijmt}} \,\forall i\in V^{G},m\in M,\,LT_{him} \le t\le T\nonumber \\ \end{aligned}$$

(7)

Setup constraints: Constraints (8) and (9) set the relationship between the processing quantity and the binary variable for the setup in each time bucket at collectors, disassemblers, shredders, and reconditioners (i.e., constraint (8)), and garbage nodes (i.e., constraint (9)), respectively.

$$\begin{aligned}&X_{imt} \le Big\_M\times Y_{it} \,\forall i\in V^{{\prime }}-V^{G},m\in M,\, 1\le t\le T\nonumber \\ \end{aligned}$$

(8)

$$\begin{aligned}&\sum \limits _{(h,i)\in L} {S_{him(t-LT_{him} )} }\nonumber \\&\le Big\_M\times Y_{it} \,\forall i\in V^{G},m\in M,\,LT_{him} \le t\le T \end{aligned}$$

(9)

Garbage Volume Limitation: Constraints (10)$\sim$(13) limits the garbage volumes generated at each collector, disassembler, shredder, and reconditioner in each time bucket.

$$\begin{aligned}&\sum \limits _{i\in V^{G}} {\sum \limits _{m\in M} {[S_{himt} \times Weight(m)]} }\nonumber \\&\quad \le Maxwaste^{C}\,\forall h\in V^{C}\hbox {, }1\le t\le T\end{aligned}$$

(10)

$$\begin{aligned}&\sum \limits _{i\in V^{G}} {\sum \limits _{m\in M} {[S_{himt} \times Weight(m)]} }\nonumber \\&\quad \le Maxwaste^{D}\,\forall h\in V^{D},\,1\le t\le T\end{aligned}$$

(11)

$$\begin{aligned}&\sum \limits _{i\in V^{G}} {\sum \limits _{m\in M} {[S_{himt} \times Weight(m)]} }\nonumber \\&\quad \le Maxwaste^{S}\,\forall h\in V^{S},\,1\le t\le T\end{aligned}$$

(12)

$$\begin{aligned}&\sum \limits _{i\in V^{G}} {\sum \limits _{m\in M} {[S_{himt} \times Weight(m)]} }\nonumber \\&\quad \le Maxwaste^{R}\,\forall h\in V^{R},\,1\le t\le T \end{aligned}$$

(13)

Other constraints: Constraint (14) sets the initial inventory at each node in time bucket 0 equal to 0. Constraint (15) sets the initial transportation quantity at each link in time bucket 0 equal to 0. Constraints (16) to (19) show the non-negative requirement for each decision variable. Constraint (20) shows the binary requirement for each binary decision variable.

$$\begin{aligned}&I_{im0} =0\quad \forall i\in V^{{\prime }}-V^{G},m\in M\end{aligned}$$

(14)

$$\begin{aligned}&S_{ijm0} =0 \quad \forall (i,j)\in L,m\in M\end{aligned}$$

(15)

$$\begin{aligned}&X_{imt} \ge 0\quad \forall i\in V^{{\prime }}-V^{G},m\in M,\,1\le t\le T\end{aligned}$$

(16)

$$\begin{aligned}&I_{imt} \ge 0\quad \forall i\in V^{{\prime }}-V^{G},m\in M,\,1\le t\le T\end{aligned}$$

(17)

$$\begin{aligned}&S_{ijmt} \ge 0\quad \forall (i,j)\in L,m\in M,\,1\le t\le T\end{aligned}$$

(18)

$$\begin{aligned}&Z_{rmt} \ge 0\quad \forall 1\le r\le d,m\in P,\,1\le t\le T\end{aligned}$$

(19)

$$\begin{aligned}&Y_{it} \in \{0,1\}\quad \forall i\in V^{{\prime }},\,1\le t\le T \end{aligned}$$

(20)

Multiple Objective Functions

In this study, a multi-phase optimization process was used to this study to solve the problem. Two objective functions had to be accomplished: (1) Minimize the total delay cost (TDC) and (2) Minimize the total operations cost of processing, transportation, inventory holding and setup (TOC) under the total delay cost (TDC) has been minimized.

Objective 1: Minimize the total delay cost, TDC.

$$\begin{aligned}&Min\,TDC=\sum \limits _{r=1}^d \left[ \sum \limits _{m\in M} DC_{rm}\times \sum \limits _{k=DUE_{rm} }^{T-1} \left( DEM_{rm}\right. \right. \\&\quad \left. \left. -\sum \limits _{t=1}^k {Z_{rmt} } \right) \right] s.t.\hbox { Constraints (1) to (20)} \end{aligned}$$

Objective 2: Minimize the total operations cost of processing, transportation, inventory holding and setup, TOC given TDC. TOC consists of six terms: (1) transportation costs between external nodes, (2) processing costs at nodes except garbage handling nodes, (3) garbage handling costs, (4) inventory holding costs at nodes except garbage handling nodes, (5) transportation costs between internal nodes, and (6) setup costs at nodes.

$$\begin{aligned}&Min\,TOC =\sum \limits _{(i,j)\in L-DL} {\sum \limits _{m\in M} {\left( TC_{ijm} \times \sum \limits _{t=1}^T {S_{ijmt}}\right) }}\nonumber \\&\quad +\sum \limits _{i\in V^{\prime }-V^{G}} \sum \limits _{m\in M} \left( PC_{in} \times \sum \limits _{t=1}^T {X_{imt}}\right) \nonumber \\&\quad +\sum \limits _{i\in V^{G}} \sum \limits _{m\in M} \left[ PCG_i \times Weight(m) \right. \nonumber \\&\quad \left. \times \sum \limits _{t=1}^T \sum \limits _{(h,i)\in L} {S_{him(t-LT_{him} )} } \right] \nonumber \\&\quad +\sum \limits _{i\in V^{\prime }-V^{G}} {\sum \limits _{m\in M} {\left( HC_{im} \times \sum \limits _{t=1}^T {I_{imt} } \right) } }\nonumber \\&\quad +\sum \limits _{(i,j)\in DL} {\sum \limits _{m\in M} {\left( {TC_{ijm} \times \sum \limits _{t=1}^T {S_{ijmt} } } \right) } }\nonumber \\&\quad +\sum \limits _{i\in V^{\prime }} {\sum \limits _{t=1}^T {(Y_{it} } \times FC_{it} )}\nonumber \\&s.t.\hbox { Constraints (1) to (20) and }\sum \limits _{r=1}^d \left[ \sum \limits _{m\in M} DC_{rm}\right. \nonumber \\&\quad \left. \times \sum \limits _{k=DUE_{rm} }^{T-1} \left( {DEM_{rm} -\sum \limits _{t=1}^k {Z_{rmt} } } \right) \right] =TDC \end{aligned}$$

(21)

In the recycling supply chain, we assumed that there are $c$ collector nodes, $d$ disassembler nodes, $s$ shredder nodes, $r$ reconditioner nodes and $g$ garbage nodes. Also there are $M$ items and material in the given product structure, $P$ recycled items and material that are in demand, $Q$ returned goods collected from customers, $O$ demands, and $T$ time buckets in the planning time horizon. In the worst case, the complexity of the recycling model will have a supply chain network with (c+d+s+r+g) nodes and $c(d+s+r+g)+d(s+r+g)+s(r+g)$+rg links. Thus, the number of decision variables and constraints can be summarized as follows.

Number of decision variables:

• 1. $X_{imt}:\, (c+d+s+r) \times M \times T$,

• 2. $S_{ijmt}:\, [c \times (d+s+r+g)+d \times (s+r+g)+s \times (r+g) +s \times g]\times M \times T$,

• 3. $I_{imt}:\, (c+d+s+r) \times M \times T$,

• 4. $Z_{rmt}:\, (O \times P \times T)$, and

• 5. $Y_{it}: \,(c+d+s+r+g)\times T$. Please note that $Y_{it}$ is a binary variable.

Number of constraints:

• 1. Constraint (1): $(c+d+s+r) \times T$,

• 2. Constraint (2): $(P \times T)$,

• 3. Constraints (3) and (4): $(O \times P)$,

• 4. Constraint (5): $(c \times Q \times T)$,

• 5. Constraint (6): $(d+s+r) \times M \times T$,

• 6. Constraint (7): $(g \times M \times T)$,

• 7. Constraint (8): $(c+d+s+r) \times M \times T$,

• 8. Constraint (9): $(g \times M \times T)$,

• 9. Constraints (10)–(13): $(c \times T),\, (d \times T),\, (s \times T)$, and $(r \times T)$,

• 10. Constraint (14): $(c+d+s+r) \times M$,

• 11. Constraint (15): $[c \times (d+s+r+g)+d \times (s+r+g)+s \times (r+g) +r \times g]\times M$,

• 12. Constraints (16) and (17): $(c+d+s+r) \times M \times T$,

• 13. Constraint (18): $[c \times (d+s+r+g)+d \times (s+r+g)+s \times (r+g) +r \times g]\times M$,

• 14. Constraint (19): $(O \times P \times T)$, and

• 15. Constraint (20): $(c+d+s+r+g)\times T$.