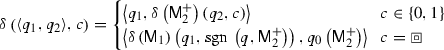Skip to main content
SpringerLink
Log in

Some Properties of Iterated Languages

  • Published:
Journal of Logic, Language and Information Aims and scope Submit manuscript

Abstract

A special kind of substitution on languages called iteration is presented and studied. These languages arise in the application of semantic automata to iterations of generalized quantifiers. We show that each of the star-free, regular, and deterministic context-free languages are closed under iteration and that it is decidable whether a given regular or determinstic context-free language is an iteration of two such languages. This result can be read as saying that the van Benthem/Keenan ‘Frege Boundary’ is decidable for large subclasses of natural language quantifiers. We also determine the state complexity of iteration of regular languages.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

Notes

  1. Dekker (2003) generalizes these results to handle more than one iteration.

  2. Many alternative characterizations exist: acceptance by a non-deterministic finite-state automaton and generation by a regular expression, for example. See Hopcroft and Ullman (1979) for details.

  3. See Diekert and Gastin (2007) for a self-contained presentation of this equivalence and others.

  4. Barwise and Cooper (1981) pioneered this approach. See Peters and Westerståhl (2006) for a comprehensive overview. Szabolcsi (2010) is an overview of quantifiers from a linguistic perspective, including some problems for the generalized quantifier approach.

  5. Note that I am using the symbols \(\forall \) and \(\exists \) to denote type \(\langle 1, 1 \rangle \) generalized quantifiers whereas they are standardly used to denote type \(\langle 1 \rangle \) quantifiers. They are, however, intimately related: the \(\langle 1, 1 \rangle \) ones here are the relativizations of the normal type \(\langle 1 \rangle \) quantifiers. See §4.4 of Peters and Westerståhl (2006).

  6. Conservativity states that \(\langle M, A , B \rangle \in Q\) iff \(\langle M, A, A \cap B \rangle \in Q\). Extension states that if \(\langle M , A , B \rangle \in Q\), then \(\langle M^\prime , A , B \rangle \in Q\) for any \(M^\prime \supseteq M\).

  7. See McMillan et al. (2005) for a neuroimaging experiment and Szymanik and Zajenkowski (2010) for a behavioral one. Clark (2011) is a useful overview of this literature.

  8. That is: \(\sigma _{L_2}\left( \varepsilon \right) = \varepsilon \), \(\sigma _{L_2}\left( aw \right) = \sigma _{L_2}\left( a \right) \sigma _{L_2}\left( w \right) \) and \(\sigma _{L_2}\left[ L_1 \right] = \bigcup _{w \in L_1} \sigma _{L_2}\left( w \right) \).

  9. See Steinert-Threlkeld and Icard III (2013) and references therein. The present definition of iteration can be seen as a more concise representation of their Definition 8.

  10. Szymanik et al. (2013) contains a preliminary experiment looking at processing consequences of semantic automata for iterated quantifiers.

  11. This definition can be re-written in more traditional function notation:

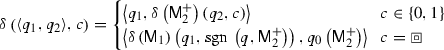
    Some readers may find this definition easier to comprehend.

  12. Thanks to Makoto Kanazawa for suggesting this proof.

  13. The ‘can’ here reflects that the present definition defines nondeterministic PDAs which, unlike in the finite-state case, are strictly more powerful than their deterministic counterparts, to be discussed below.

  14. These languages can equally be characterized as those generated by a context-free grammar.

  15. Theorem 6 of Steinert-Threlkeld and Icard III (2013) states this result as a full closure result for context-free languages. This is because in that paper, the authors assumed—in addition to conservativity and extension—the isomorphism closure of quantifiers, which has the result that all of the languages discussed were permutation-closed. While this assumption is often made, natural language determiners like ‘the first five’ and ‘every other’ seem to be counterexamples.

  16. As presently defined, a DPDA may not read the entire input. However, for every DPDA \({\mathsf {M}}\), there is another DPDA \({\mathsf {M}}^\prime \) that does read the entire input such that \(L\left( {\mathsf {M}} \right) = L\left( {\mathsf {M}}^\prime \right) \). See Lemma 10.3 (p. 236) of Hopcroft and Ullman (1979). Because of this, in what follows we will assume that all DPDAs read the entire input.

  17. McWhirter (2014) has obtained this result independently. My exposition of this result has improved greatly from reading her work.

  18. See Giammarresi and Restivo (1997) for details.

References

  • Barwise, J., & Cooper, R. (1981). Generalized quantifiers and natural language. Linguistics and Philosophy, 4(2), 159–219.

    Article  Google Scholar 

  • Clark, R. (2011). Generalized quantifiers and number sense. Philosophy Compass, 6(9), 611–621.

    Article  Google Scholar 

  • Cui, B., Gao, Y., Kari, L., & Sheng, Y. (2012). State complexity of combined operations with two basic operations. Theoretical Computer Science, 437, 82–102. doi:10.1016/j.tcs.2012.02.030.

    Article  Google Scholar 

  • Dekker, P. (2003). Meanwhile, within the Frege boundary. Linguistics and Philosophy, 26(5), 547–556.

    Article  Google Scholar 

  • Diekert, V., & Gastin, P. (2007). First-order definable languages. In J. Flum, E. Grädel, & T. Wilke (Eds.), Logic and automata: History and perspectives, Texts in Logic and Games (pp. 261–306). Amsterdam: Amsterdam University Press.

    Google Scholar 

  • Giammarresi, D., & Restivo, A. (1997). Two-dimensional languages. In G. Rozenberg & A. Salomaa (Eds.), Handbook of formal languages (vol 3): Beyond words (Vol. 3, pp. 215–268). Berlin: Springer.

    Chapter  Google Scholar 

  • Hopcroft, J. E., & Ullman, J. D. (1979). Introduction to automata theory, languages, and computation. Reading: Addison-Wesley.

    Google Scholar 

  • Kanazawa, M. (2013). Monadic Quantifiers Recognized by Deterministic Pushdown Automata. In M. Aloni, M. Franke, & F. Roelofsen (Eds.), Proceedings of the 19th Amsterdam Colloquium (pp. 139–146).

  • Keenan, E. L. (1992). Beyond the Frege boundary. Linguistics and Philosophy, 15(2), 199–221.

    Article  Google Scholar 

  • Keenan, E. L. (1996). Further beyond the Frege boundary. In J. van der Does & J. van Eijck (Eds.), Quantifiers, logic, and language, volume 54 of CSLI Lecture Notes (pp. 179–201). Stanford: CSLI Publications.

    Google Scholar 

  • Lindström, P. (1966). First order predicate logic with generalized quantifiers. Theoria, 32(3), 186–195.

    Google Scholar 

  • McMillan, C. T., Clark, R., Moore, P., Devita, C., & Grossman, M. (2005). Neural basis for generalized quantifier comprehension. Neuropsychologia, 43(12), 1729–1737. doi:10.1016/j.neuropsychologia.2005.02.012.

    Article  Google Scholar 

  • McNaughton, R., & Papert, S. A. (1971). Counter-free automata, volume 65 of MIT Research Monographs. Cambridge: The MIT Press.

    Google Scholar 

  • McWhirter, S. (2014). An automata-theoretic perspective on polyadic quantification in natural language. Masters of logic thesis, Universiteit van Amsterdam.

  • Mostowski, A. (1957). On a generalization of quantifiers. Fundamenta Mathematicae, 44(2), 12–36.

    Google Scholar 

  • Mostowski, M. (1998). Computational semantics for monadic quantifiers. Journal of Applied Non-classical Logics, 8(1–2), 107–121.

    Article  Google Scholar 

  • Peters, S., & Westerståhl, D. (2006). Quantifiers in language and logic. Oxford: Clarendon Press.

    Google Scholar 

  • Sénizergues, G. (1997). The equivalence problem for deterministic pushdown automata is decidable. In P. Degano, R. Gorrieri, & A. Marchetti-Spaccamela (Eds.), Automata, Languages and Programming, Volume 1256 of Lecture Notes in Computer Science (pp. 671–681). Berlin: Springer.

    Google Scholar 

  • Sénizergues, G. (2001). L(A) = L(B)? Decidability results from complete formal systems. Theoretical Computer Science, 251(1–2), 1–166.

    Article  Google Scholar 

  • Sénizergues, G. (2002). L(A) = L(B)? A simplified decidability proof. Theoretical Computer Science, 281(1–2), 555–608.

    Article  Google Scholar 

  • Steinert-Threlkeld, S. (2014). On the decidability of iterated languages. In Oleg, P. (Ed.), Proceedings of philosophy, mathematics, linguistics: Aspects of interaction (PhML2014), (pp. 215–224).

  • Steinert-Threlkeld, S., & Icard III, T. F. (2013). Iterating semantic automata. Linguistics and Philosophy, 36(2), 151–173. doi:10.1007/s10988-013-9132-6.

    Article  Google Scholar 

  • Szabolcsi, A. (2010). Quantification. Research surveys in linguistics. Cambridge: Cambridge University Press.

  • Szymanik, J., & Zajenkowski, M. (2010). Comprehension of simple quantifiers: Empirical evaluation of a computational model. Cognitive Science, 34(3), 521–532. doi:10.1111/j.1551-6709.2009.01078.x.

    Article  Google Scholar 

  • Szymanik, J., Steinert-Threlkeld, S., Zajenkowski, M., Icard III, T. F. (2013). Automata and complexity in multiple-quantifier sentence verification. In Proceedings of the 12th international conference on cognitive modeling.

  • van Benthem, J. (1986). Essays in logical semantics. Dordrecht: D. Reidel Publishing Company.

    Book  Google Scholar 

  • van Benthem, J. (1989). Polyadic quantifiers. Linguistics and Philosophy, 12(4), 437–464. doi:10.1007/BF00632472.

    Article  Google Scholar 

  • Yu, S., Zhuang, Q., & Salomaa, K. (1994). The state complexities of some basic operations on regular languages. Theoretical Computer Science, 125(2), 315–328. doi:10.1016/0304-3975(92)00011-F.

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Philosophy, Stanford University, Stanford, CA, USA

    Shane Steinert-Threlkeld

Authors
  1. Shane Steinert-Threlkeld
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Shane Steinert-Threlkeld.

Additional information

I thank Johan van Benthem, Thomas Icard, Makoto Kanazawa, Christopher Potts, and Jakub Szymanik for helpful discussions. Two anyonymous referees provided very helpful comments. An earlier version of this paper was presented at Philosophy, Mathematics, Linguistics: Aspects of Interaction (PhML2014) in St. Petersburg, Russia (see Steinert-Threlkeld 2014). I am grateful to the organizers and participants there. In particular, I must express deep gratitude to the late Grisha Mints, whose love of logic was matched by his warmth of heart and sense of humor. You were an inspiration.

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Steinert-Threlkeld, S. Some Properties of Iterated Languages. J of Log Lang and Inf 25, 191–213 (2016). https://doi.org/10.1007/s10849-016-9239-6

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10849-016-9239-6

Keywords

Search

Navigation