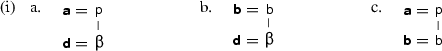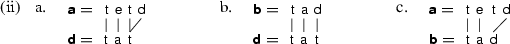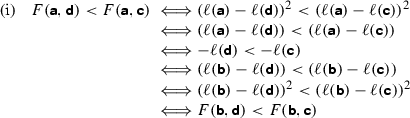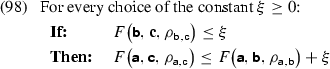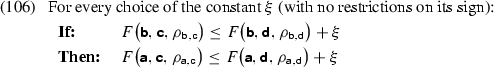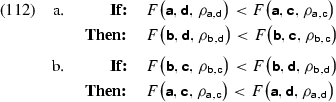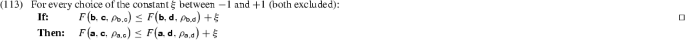Abstract
Idempotency requires any phonotactically licit forms to be faithfully realized. Output-drivenness requires any discrepancies between underlying and output forms to be driven exclusively by phonotactics. These formal notions are relevant for phonological theory (they capture counter-feeding and counter-bleeding opacity) and play a crucial role in learnability. Tesar (Output-driven phonology: theory and learning. Cambridge studies in linguistics, 2013) and Magri (J of Linguistics, 2017) provide tight guarantees for OT output-drivenness and idempotency through conditions on the faithfulness constraints. This paper derives analogous faithfulness conditions for HG idempotency and output-drivenness and develops an intuitive interpretation of the various OT and HG faithfulness conditions thus obtained. The intuition is that faithfulness constraints measure the phonological distance between underlying and output forms. They should thus comply with a crucial axiom of the definition of distance, namely that any side of a triangle is shorter than the sum of the other two sides. This intuition leads to a faithfulness triangle inequality which is shown to be equivalent to the faithfulness conditions for idempotency and output-drivenness. These equivalences hold under various assumptions, crucially including McCarthy’s (Phonology 20(1):75–138, 2003b) generalization that (faithfulness) constraints are all categorical.
Similar content being viewed by others
Notes
Properties of the candidate set also play a crucial role in shaping a typology. This introductory section offers only an informal preview of the main results and thus omits various candidate conditions which will be discussed in the rest of the paper.
Correspondence relations might want to distinguish between multiple occurrences of the same segment in a string. Thus, correspondence relations cannot be defined simply as relations between the two sets of underlying and surface segments. To keep the presentation straightforward, the paper will follow common practice and ignore these subtleties.
The operation of composition between two relations is usually denoted by “\(\circ \)”. In the rest of the paper, I write more succinctly \(\rho _{{{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{b}}}}}} \rho _{{{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{c}}}}}}\) instead of \(\rho _{{{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{b}}}}}} \circ \rho _{{{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{c}}}}}}\).
Besides the triangle inequality, the abstract definition of distance requires two additional axioms. The first axiom is symmetry, which requires the distance between two points to be insensitive to their order. The second axiom is the identity of the indiscernibles, which requires two points to coincide if and only if they have zero distance. Together with the triangle inequality, these axioms ensure the non-negativity of a distance. Symmetry fails for core faithfulness constraints such as Max and Dep. Half of the identity of the indiscernibles is enforced by the definitional condition (8) of faithfulness constraints: if the underlying and surface forms coincide (and the correspondence relation is the identity), their faithfulness violations are equal to zero. But the other half of the identity of the indiscernibles fails, as faithfulness constraints are satisfied by less than perfect string identity.
As stressed by a reviewer, the triangle inequality is applied here to each faithfulness constraint individually, rather than to some aggregation (e.g., a weighted sum) of their number of violations.
For any two strings \({{\mathbf {\mathsf{{a}}}}}\) and \({{\mathbf {\mathsf{{b}}}}}\), the notation \({{\mathbf {\mathsf{{a}}}}}\subseteq {{\mathbf {\mathsf{{b}}}}}\) indicates that \({{\mathbf {\mathsf{{a}}}}}\) is a subsequence of \({{\mathbf {\mathsf{{b}}}}}\): \({{\mathbf {\mathsf{{a}}}}}\) is obtained from \({{\mathbf {\mathsf{{b}}}}}\) by replacing some symbols of \({{\mathbf {\mathsf{{b}}}}}\) with the empty symbol.
In other words,
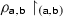 is the set of those pairs \(({\textsf {a}}', {\textsf {b}}')\) in \(\rho _{{{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{b}}}}}}\) such that \({\textsf {a}}' = {\textsf {a}}\). Once the underlying string \({{\mathbf {\mathsf{{a}}}}}\) is restricted to a single segment \({\textsf {a}}\), the correspondence relation \(\rho _{{{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{b}}}}}}\) must necessarily be restricted to
is the set of those pairs \(({\textsf {a}}', {\textsf {b}}')\) in \(\rho _{{{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{b}}}}}}\) such that \({\textsf {a}}' = {\textsf {a}}\). Once the underlying string \({{\mathbf {\mathsf{{a}}}}}\) is restricted to a single segment \({\textsf {a}}\), the correspondence relation \(\rho _{{{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{b}}}}}}\) must necessarily be restricted to 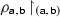 . In fact, the triplet \(({\textsf {a}}, {{\mathbf {\mathsf{{b}}}}}, \rho _{{{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{b}}}}}})\) (with the singleton underlying segment \({\textsf {a}}\) and the original correspondence relation \(\rho _{{{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{b}}}}}}\)) does not count as a candidate according to the assumption (2) that correspondence relations hold between the segments of the two strings in the candidate.
. In fact, the triplet \(({\textsf {a}}, {{\mathbf {\mathsf{{b}}}}}, \rho _{{{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{b}}}}}})\) (with the singleton underlying segment \({\textsf {a}}\) and the original correspondence relation \(\rho _{{{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{b}}}}}}\)) does not count as a candidate according to the assumption (2) that correspondence relations hold between the segments of the two strings in the candidate.A subsequence needs not consist of contiguous elements, contrary to a substring: itk is both a subsequence and a substring of pitkol, while ptkl is a subsequence but not a substring. It might be possible to define I-additivity in terms of a sum over sub-strings of contiguous segments, rather than over sub-sequences of possibly non-contiguous strings. For Linearity-type constraints, this modification would capture Heinz’s (2005) proposal that only immediate precedence matters in the definition of the faithfulness constraints. Switching from sub-sequences to sub-strings would also have implications for Adjacency-type constraints. They have been defined in (15) and (17) as counting over corresponding pairs, whereby they qualify as C-categorical. An alternative definition of, say, I-Adjacency would be the following: it assigns to a candidate \(({{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{b}}}}}, \rho _{{{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{b}}}}}})\) a number of violations equal to the number of underling adjacent pairs of segments which have no adjacent surface correspondents. If I-additivity is redefined in terms of sub-strings, then I-Adjacency qualifies as I-additive (it would not count as I-additive according to the definition in terms of sub-sequences).
This implies that the shared correspondence relation must hold between the shared surface string \({{\mathbf {\mathsf{{b}}}}}\) and the “smaller” underlying string \({{\mathbf {\mathsf{{a}}}}}\).
The alternative definition of I-Adjacency in footnote 8 makes it I-additive. Crucially, it is also O-monotone: adding surface segments can only disrupt surface adjacency and thus increase the number of violations. Analogous considerations hold for O-Adjacency.
The assumption that a grammar G maps an underlying form to a single candidate is not crucial: the analyses developed here extend to a framework where G maps an underlying form to a set of candidates, thus modeling phonological variation.
As noted in footnote 11, I assume that grammars map an underlying form to a single candidate. This condition holds in OT provided the constraint set is sufficiently rich relative to the candidate set: for any two candidates \(({{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{b}}}}}, \rho _{{{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{b}}}}}})\) and \(({{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{c}}}}}, \rho _{{{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{c}}}}}})\) which share the underlying form \({{\mathbf {\mathsf{{a}}}}}\), the constraint set contains a constraint C which prefers one of the two.
MCarthy and Prine’s (1995) definition of I-/O-Contiguity makes them binary.
A close look at the proof of Proposition 3 shows that, if the faithfulness constraint F is I-categorical of order \(\ell \,{=}\,1\), the one-to-one assumption can be weakened to the assumption that no correspondence relation coalesces any two underlying segments into a single surface segment. If the faithfulness constraint F is O-categorical of order \(\ell =1\), the one-to-one assumption can be weakened to the assumption that no correspondence relation breaks any underlying segment into two surface segments. If the faithfulness constraint F is instead C-categorical, the one-to-one assumption cannot be weakened, not even in the case \(\ell =1\).
In fact, assume that the quantity \(F({{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{c}}}}}, \rho _{{{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{b}}}}}} \rho _{{{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{c}}}}}})\) in the left-hand side of the inequality in the consequent of the FIC\(_{\text {comp}}^{\text {OT}}\) is larger than 0 (otherwise, the inequality trivially holds). This means that \({{\mathbf {\mathsf{{c}}}}}\) has length 1. The antecedent \(F({{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{c}}}}}, \rho _{{{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{c}}}}}} )=0\) of the FIC\(_{\text {comp}}^{\text {OT}}\) thus requires every segment of \({{\mathbf {\mathsf{{b}}}}}\) to have a correspondent in \({{\mathbf {\mathsf{{c}}}}}\). Since correspondence relations are one-to-one, the string \({{\mathbf {\mathsf{{b}}}}}\) must consist of a single segment which is put in correspondence by \(\rho _{{{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{c}}}}}}\) with the single segment of \({{\mathbf {\mathsf{{c}}}}}\). It then follows that every underlying segment \({\textsf {a}}\) of \({{\mathbf {\mathsf{{a}}}}}\) which violates F relative to the composition candidate \(({{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{c}}}}}, \rho _{{{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{b}}}}}} \rho _{{{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{c}}}}}})\) also violates F relative to the candidate \(({{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{b}}}}}, \rho _{{{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{b}}}}}})\), thus establishing the inequality in the consequent of the FIC\(_{\text {comp}}^{\text {OT}}\).
Analogous considerations hold for Integrity (which is I-categorical and O-monotone) and Uniformity (which is O-categorical and I-monotone). I ignore these two constraints here, because Proposition 4 requires correspondence relations to be one-to-one.
The implication (45) trivially holds also for \(\xi < 0\), because the antecedent is always false in that case, due to the non-negativity of constraint violations.
The second FODC\(^{\text {OT}}\) implication (58b) is trivially satisfied in the special case where \(({{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{d}}}}}, \rho _{{{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{d}}}}}}) = ({{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{b}}}}}, \mathbb {I}_{{{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{b}}}}}})\), because its antecedent \(F({{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{c}}}}}, \rho _{{{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{c}}}}}}) < F({{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{d}}}}}, \rho _{{{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{d}}}}}})\) becomes \(F({{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{c}}}}}, \rho _{{{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{c}}}}}}) < 0\), which contradicts the non-negativity of constraint violations.
This means that there exists a mapping from the segments of \({{\mathbf {\mathsf{{b}}}}}\) deleted relative to \(({{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{d}}}}}, \rho _{{{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{d}}}}}})\) to the segments of \({{\mathbf {\mathsf{{a}}}}}\) deleted relative to \(({{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{d}}}}}, \rho _{{{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{d}}}}}})\) such that two different deleted segments of \({{\mathbf {\mathsf{{b}}}}}\) correspond to two different deleted segments of \({{\mathbf {\mathsf{{a}}}}}\). In other words, \(({{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{d}}}}}, \rho _{{{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{d}}}}}})\) has at least as many deleted segments as \(({{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{d}}}}}, \rho _{{{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{d}}}}}})\).
This failure of output-drivenness comes, as expected, with a failure of the FODC\(^{\text {OT}}\). Indeed, the first FODC\(^{\text {OT}}\) (58a) fails for \(F = \text{ Ident }_{\text {[voice]}}\): \(\text{ Id }({{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{d}}}}}) = 0\) and \(\text{ Id }({{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{c}}}}}) = 1\), so that the antecedent of the first FODC\(^{\text {OT}}\) (58a) holds; yet \(\text{ Id }({{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{d}}}}}) = \text{ Id }({{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{c}}}}}) = 0\), so that its consequent fails. Other choices of the correspondence relation \(\rho _{{{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{c}}}}}}\) yield analogous failures. For instance, suppose that \(\rho _{{{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{c}}}}}}\) establishes no correspondence between the codas of \({{\mathbf {\mathsf{{a}}}}}\) and \({{\mathbf {\mathsf{{c}}}}}\). In this case, the second FODC\(^{\text {OT}}\) (58b) fails for \(F = \text{ Max }\): \(\text{ Max }({{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{c}}}}}) = 0\) and \(\text{ Max }({{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{d}}}}}) = 1\), so that the antecedent of the second FODC\(^{\text {OT}}\) (58b) holds; yet \(\text{ Max }({{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{c}}}}}) = \text{ Max }({{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{d}}}}}) = 1\), so that its consequent fails.
Tesar defines the similarity order concretely in terms of (identity, deletion, and insertion) disparities between strings and correspondence relations in order for the resulting notion of output-drivenness to be framework-independent and thus to be able to bridge rule-based and constraint-based phonology. Yet, I submit that a disparity is really nothing else than a new technical term to denote a faithfulness constraint violation. Furthermore, Tesar does not shy away from correspondence relations, although they also are strictly speaking not framework-independent, but rather a representational device needed in constraint-based phonology to get around the lack of phonological derivations. Yet, Tesar (p. 34) objects that, “while in linguistics the terminology of correspondence is perhaps found most explicitly in the OT literature, the concept is equally important to any generative theory. There is a correspondence relation implicit in every SPE-style rule.” I submit that the same argument applies to faithfulness constraints: although they were only formalized in OT, faithfulness considerations are plausibly intrinsic to phonology, no matter the framework. I conclude that there is no impediment against rephrasing Tesar’s definition of the similarity order in terms of faithfulness constraints.
Consider again the candidates \(({{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{d}}}}}, \rho _{{{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{d}}}}}})\) and \(({{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{d}}}}}, \rho _{{{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{d}}}}}})\) in (55), repeated below in (ia) and (ib). In order to secure the argument made in Sect. 5.1.3, we need to secure the similarity inequality \(({{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{d}}}}}, \rho _{{{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{d}}}}}}) \le _{\text {sim}}^{\mathcal {F}} ({{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{d}}}}}, \rho _{{{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{d}}}}}})\) with \(\mathcal {F}= \{ \text{ Ident }_{\text {[voice]}}, \text{ Ident }_{\text {[cont]}}\}\). Indeed, condition (68) holds for both faithfulness constraints in \(\mathcal {F}\) when the candidate \(({{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{b}}}}}, \rho _{{{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{b}}}}}})\) in the additional term of (68) is defined as in (ic).
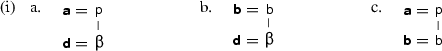
Consider next the candidates \(({{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{d}}}}}, \rho _{{{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{d}}}}}})\) and \(({{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{d}}}}}, \rho _{{{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{d}}}}}})\) in (56), repeated below in (iia) and (iib). In order to secure the argument made in Sect. 5.2.1, we need to secure the similarity inequality \(({{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{d}}}}}, \rho _{{{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{d}}}}}}) \le _{\text {sim}}^\mathcal {F} ({{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{d}}}}}, \rho _{{{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{d}}}}}})\) with \(\mathcal {F}= \{ \text{ Ident }_{\text {[voice]}}, \text{ Ident }_{\text {[low]}} \}\). Indeed, condition (68) holds for both faithfulness constraints in \(\mathcal {F}\) when the candidate \(({{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{b}}}}}, \rho _{{{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{b}}}}}})\) in the additional term in (68) is defined as in (iic).
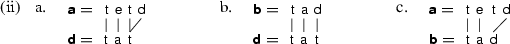
Consider the first FODC\(_{\text {comp}}^{\text {OT}}\) implication (74a). Its antecedent and consequent are shown to be equivalent in (i), using the fact that \(x < y\) iff \(x^2 < y^2\), for any \(x, y\ge 0\)
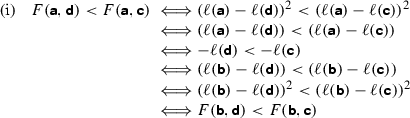
An analogous reasoning holds for the second FODC\(_{\text {comp}}^{\text {OT}}\) implication (74b).
In fact \(F({{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{c}}}}}) = ( \ell ({{\mathbf {\mathsf{{a}}}}}) - \ell ({{\mathbf {\mathsf{{c}}}}}) )^2 = [ ( \ell ({{\mathbf {\mathsf{{a}}}}}) - \ell ({{\mathbf {\mathsf{{b}}}}}) ) + ( \ell ({{\mathbf {\mathsf{{b}}}}}) - \ell ({{\mathbf {\mathsf{{c}}}}}) ) ]^2\ge ( \ell ({{\mathbf {\mathsf{{a}}}}}) - \ell ({{\mathbf {\mathsf{{b}}}}}) )^2 + ( \ell ({{\mathbf {\mathsf{{b}}}}}) - \ell ({{\mathbf {\mathsf{{c}}}}}) )^2= F({{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{b}}}}}) + F({{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{c}}}}})\), contradicting the FTI\(_{\text {comp}}\).
I am assuming that the correspondence relation \(\rho _{{{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{b}}}}}}\) in the candidate \(({{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{b}}}}}, \rho _{{{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{b}}}}}}) = (\text{/p/ }, \text{[b] })\) does put the singleton underlying and surface segments in correspondence. If that is not the case, then the inequality (79) would indeed succeed for \(F = \text{ Ident }_{\text {[voice]}} \vee \text{ Ident }_{\text {[cont]}}\) but it would fail for \(F = \text{ Max }\) and \(F = \text{ Dep }\).
As explained in footnote 17, it makes no difference whether the constant \(\xi \) in (45)/(82) is restricted to be non-negative or allowed to be negative. That is of course not the case for (80): the fact that \(\xi \) is allowed to be negative makes it a stronger condition.
References
Blaho, S., Bye, P., & Krämer, M. (2007). Freedom of analysis?. Berlin: Mouton de Gruyter.
Bolognesi, R. (1998). The phonology of Campidanian Sardinian: A unitary account of self-organizing structure. Ph.D. thesis, University of Amsterdam, Amsterdam.
Buccola, B. (2013). On the expressivity of Optimality Theory versus ordered rewrite rules. In G. Morrill & M. Nederhof (Eds.), Proceedings of formal grammar 2012 and 2013, Lecture notes in computer science. Springer, Heidelberg.
Carpenter, A. (2002). Noncontiguous metathesis and Adjacency. In A. Carpenter, A. Coetzee, & P. de Lacy (Eds.), Papers in optimality theory (Vol. 2, pp. 1–26). Amherst, MA: GLSA.
Casali, R. F. (1997). Vowel elision in hiatus contexts: Which vowel goes? Language, 73, 493–533.
Casali, R. F. (1998). Resolving Hiatus. Outstanding dissertations in Linguistics, Garland, New York
Downing, L. J. (1998). On the prosodic misalignment of onsetless syllables. Natural Language and Linguistic Theory, 16, 1–52.
Downing, L. J. (2000). Morphological and prosodic constraints on Kinande verbal reduplication. Phonology, 17, 1–38.
Flack, K. (2007). Inducing functionally grounded constraints. In M. Becker (Ed.), Papers in theoretical and computational phonology, UMOP (University of Massachusetts Occasional Papers) 36 (pp. 13–44). GLSA: Amherst, MA.
Hayes, B. (2004). Phonological acquisition in optimality theory: The early stages. In R. Kager, J. Pater, & W. Zonneveld (Eds.), Constraints in Phonological Acquisition (pp. 158–203). Cambridge: Cambridge University Press.
Heinz, J. (2005). Reconsidering linearity: Evidence from CV metathesis. In J. Alderete, C. Han, & A. Kochetov (Eds.), Proceedings of WCCFL 24 (pp. 200–208). Somerville, MA: Cascadilla Press.
Keller, F. (2000). Gradience in grammar. Experimental and computational aspects of degrees of grammaticality. Ph.D. thesis, University of Edinburgh, England
Kubozono, H., Ito, J., & Mester, A. (2008). Consonant gemination in Japanese loanword phonology. In Current issues in unity and diversity of languages. Collection of papers selected from the 18th international congress of linguists (pp. 953–973). Dongan-gu: Dongam Publishing Co.
Legendre, G., Miyata, Y., & Smolensky, P. (1990a). Harmonic grammar: A formal multi-level connectionist theory of linguistic well-formedness: An application. In M. A. Gernsbacher & S. J. Derry (Eds.), Annual conference of the Cognitive Science Society 12 (pp. 884–891). Mahwah, NJ: Lawrence Erlbaum Associates.
Legendre, G., Miyata, Y., & Smolensky, P. (1990b). Harmonic grammar: A formal multi-level connectionist theory of linguistic well-formedness: Theoretical foundations. In M. A. Gernsbacher & S. J. Derry (Eds.), Annual conference of the Cognitive Science Society 12 (pp. 388–395). Mahwah, NJ: Lawrence Erlbaum.
Legendre, G., Sorace, A., & Smolensky, P. (2006). The optimality theory/harmonic grammar connection. In P. Smolensky & G. Legendre (Eds.), The harmonic mind (pp. 903–966). Cambridge, MA: MIT Press.
Lombardi, L. (2001). Why place and voice are different: Constraint interactions and feature faithfulness in optimality theory. In L. Lombardi (Ed.), Segmental phonology in optimality theory: Constraints and representations (pp. 13–45). Cambridge: Cambridge University Press.
Łubowicz, A. (2002). Derived environment effects in oprimality theory. Lingua, 112, 243–280.
Łubowicz, A. (2011). Chain shifts. In M. van Oostendorp, C. Ewen, E. Hume, & K. Rice (Eds.), Companion to phonology (pp. 1717–1735). New York: Wiley.
Magri, G. (2017). Idempotency in optimality theory. Journal of Linguistics. doi:10.1017/S0022226717000019.
Magri, G. (to appear b). A note on phonological similarity in Tesar’s (2013) theory of output-drivenness. Journal of Logic and Computation.
Magri, G. (to appear c). Output-drivenness and partial phonological features. Linguistic Inquiry.
McCarthy, J. J. (1994). Comparative markedness (long version). In A. Carpenter, A. Coetzee & P. de Lacy (Eds.), Papers in Optimality Theory II. University of Massachusetts Occasional Papers in Linguistics (Vol. 26). Graduate Linguistic Students’ Association, Umass.
McCarthy, J. J. (2003a). Comparative markedness. Theoretical Linguistics, 29, 1–51.
McCarthy, J. J. (2003b). OT constraints are categorical. Phonology, 20(1), 75–138.
McCarthy, J. J., & Prince, A. (1995). Faithfulness and reduplicative identity. In J. Beckman, S. Urbanczyk, & L. Walsh Dickey (Eds.), University of Massachusetts occasional papers in linguistics 18: Papers in optimality theory (pp. 249–384). Amherst: GLSA.
Moreton, E. (2004). Non-computable functions in optimality theory. In J. J. McCarthy (Ed.), Optimality theory in phonology: A reader (pp. 141–163). Malden, MA: Wiley.
Moreton, E., & Smolensky, P. (2002). Typological consequences of local constraint conjunction. In L. Mikkelsen & C. Potts (Eds.), WCCFL 21: Proceedings of the 21st annual conference of the West Coast conference on formal linguistics (pp. 306–319). Cambridge, MA: Cascadilla Press.
Prince, A. (2007). The pursuit of theory. In P. de Lacy (Ed.), The Cambridge handbook of phonology (pp. 33–60). Cambridge: Cambridge University Press.
Prince, A., & Smolensky, P. (2004). Optimality theory: Constraint interaction in generative grammar. Blackwell, Oxford, as Technical Report CU-CS-696-93, Department of Computer Science, University of Colorado at Boulder, and Technical Report TR-2, Rutgers Center for Cognitive Science, Rutgers University, New Brunswick, NJ, 1993. Also available as ROA 537 version.
Prince, A., & Tesar, B. (2004). Learning phonotactic distributions. In R. Kager, J. Pater, & W. Zonneveld (Eds.), Constraints in phonological acquisition (pp. 245–291). Cambridge: Cambridge University Press.
Rudin, W. (1953). Principles of mathematical analysis. New York City: McGraw-Hill Book Company.
Smolensky, P. (1995). On the internal structure of the constraint component of UG. http://roa.rutgers.edu/article/view/87, colloquium presented at the University of California, Los Angeles, April 7, 1995. Handout available as ROA-86 from the Rutgers Optimality Archive.
Smolensky, P., & Legendre, G. (2006). The harmonic mind. Cambridge, MA: MIT Press.
Tesar, B. (2013). Output-driven phonology: Theory and Learning. Cambridge studies in linguistics.
Walker, R. (1999). Esimbi vowel height shift: Implications for faith and markedness. http://roa.rutgers.edu/article/view/346. University of Southern California. Available as ROA-336 from the Rutgers Optimality Archive.
Wheeler, M. W. (2005). Cluster reduction: Deletion or coalescence? Catalan Journal of Linguistics, 4, 57–82.
White, J. (2013). Bias in phonological learning: Evidence from saltation. Ph.D. thesis, UCLA.
Author information
Authors and Affiliations
Corresponding author
Additional information
The research reported in this paper has been supported by a Marie Curie Intra European Fellowship (Grant Agreement Number: PIEF-GA-2011-301938) and by an MIT-France seed Grant. Parts of this paper have been presented at WCCFL 33 in March 2015; at the EPG (Experimental Phonology Group) seminar at Utrecht University in June 2015; at the LSA Workshop on Computational Phonology and Morphology at the University of Chicago in July 2015; at the Rutgers Optimality Research Group in September 2015; at OCP 13 in January 2016; and at MIT in April 2016. Feedback from those audiences is gratefully acknowledged. Finally, I would like to thank Bruce Tesar for very useful comments on earlier versions of this paper.
A Proofs
A Proofs
Throughout this appendix, I consider four strings \({{\mathbf {\mathsf{{a}}}}}\), \({{\mathbf {\mathsf{{b}}}}}\), \({{\mathbf {\mathsf{{c}}}}}\), and \({{\mathbf {\mathsf{{d}}}}}\), whose generic segments are denoted by \({\textsf {a}}\), \({\textsf {b}}\), \({\textsf {c}}\), \({\textsf {d}}\). For readability, I use statements such as “for every/some segment \({\textsf {a}}\)” as a shorthand for “for every/some segment \({\textsf {a}}\) of the string \({{\mathbf {\mathsf{{a}}}}}\)”, thus leaving the domain of the quantifier implicit.
1.1 A.1 Proof of Proposition 3
-
Proposition 3 Assume the candidate set (2) satisfies the transitivity axiom (6) and only contains one-to-one correspondence relations. Consider a faithfulness constraint F which is C-categorical; or I-categorical and O-monotone; or O-categorical and I-monotone. F satisfies the FIC \(_{\text {comp}}^{\,\text {OT}}\) if and only if it satisfies the FTI \(_{\text {comp}}\). \(\square \)
Proof
As shown in Sect. 3.3.1, the FTI\(_{\text {comp}}\) entails the FIC\(_{\text {comp}}^{\text {OT}}\) in the general case. To prove the reverse entailment, consider a faithfulness constraint F which satisfies the FIC\(_{\text {comp}}^{\text {OT}}\) repeated in (87) for any two candidates \(( {{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{b}}}}}, \rho _{{{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{b}}}}}} )\) and \(( {{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{c}}}}}, \rho _{{{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{c}}}}}} )\) and their composition candidate \(({{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{c}}}}}, \rho _{{{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{b}}}}}}\rho _{{{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{c}}}}}})\), and let me show that F then satisfies the FTI\(_{\text {comp}}\) repeated in (88).

For concreteness, the rest of the proof considers the case where F is I-categorical of order \(\ell \) and O-monotone, so that it satisfies the I-additivity condition repeated in (89); the cases where F is instead C-categorical or O-categorical and I-monotone are treated analogously.

The I-additivity condition (89) entails that F assigns zero violations to candidates whose underlying string is shorter than \(\ell \), as the sum on the right-hand side is empty in this case (there are no subsequences of length \(\ell \)). The FTI\(_{\text {comp}}\) (88) thus trivially holds when its string \({{\mathbf {\mathsf{{a}}}}}\) is shorter than \(\ell \), because its left-hand side \(F ( {{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{c}}}}}, \rho _{{{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{b}}}}}}\rho _{{{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{c}}}}}} )\) is equal to zero. From now on, I assume therefore that the string \({{\mathbf {\mathsf{{a}}}}}\) has length at least \(\ell \).
Consider a subsequence \({\textsf {a}}_1 \cdots {\textsf {a}}_\ell \) of \({{\mathbf {\mathsf{{a}}}}}\) of length \(\ell \). Let \({{\mathbf {\mathsf{{b}}}}}_{{\textsf {a}}_1\cdots {\textsf {a}}_\ell }\) be the subsequence in \({{\mathbf {\mathsf{{b}}}}}\) which is the surface correspondent of the underlying subsequence \({\textsf {a}}_1 \cdots {\textsf {a}}_\ell \) relative to the correspondence relation \(\rho _{{{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{b}}}}}}\) (namely, \({{\mathbf {\mathsf{{b}}}}}_{{\textsf {a}}_1\cdots {\textsf {a}}_\ell }\) is the subsequence of \({{\mathbf {\mathsf{{b}}}}}\) consisting of all and only the segments which are in correspondence with one of the segments \({\textsf {a}}_1,\ldots , {\textsf {a}}_\ell \)). The operations of composition and restriction over correspondence relations commute in the sense of the identity (90): the restriction of the composition correspondence relation \(\rho _{{{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{b}}}}}} \rho _{{{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{c}}}}}}\) to the pair of strings \(({\textsf {a}}_1\cdots {\textsf {a}}_\ell , {{\mathbf {\mathsf{{c}}}}})\) coincides with the composition of the restrictions of the relations \(\rho _{{{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{b}}}}}}\) and \(\rho _{{{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{c}}}}}}\) to the pairs of strings \(({\textsf {a}}_1\cdots {\textsf {a}}_\ell , {{\mathbf {\mathsf{{b}}}}}_{{\textsf {a}}_1 \cdots {\textsf {a}}_\ell })\) and \(({{\mathbf {\mathsf{{b}}}}}_{{\textsf {a}}_1\cdots {\textsf {a}}_\ell }, {{\mathbf {\mathsf{{c}}}}})\).

The identity (90) says that the candidate (91c) is the composition of the two candidates (91a) and (91b).

The hypothesis that F satisfies the FIC\(_{\text {comp}}^{\text {OT}}\) (87) for these two candidates (91a) and (91b) and their composition candidate (91c) becomes:

Since F is I-categorical of order \(\ell \) and since the underlying string \({\textsf {a}}_1 \cdots {\textsf {a}}_\ell \) has length \(\ell \), the left-hand side of the inequality in the consequent of (92) is equal to either 0 or 1. By reasoning as in Sect. 3.3.2, the FIC\(_{\text {comp}}^{\text {OT}}\) (92) thus entails the FTI\(_{\text {comp}}\) (93).

The rest of the proof obtains the FTI\(_{\text {comp}}\) (88) by summing the inequality (93) over all subsequences \({\textsf {a}}_1\cdots {\textsf {a}}_\ell \) of length \(\ell \) of the underlying string \({{\mathbf {\mathsf{{a}}}}}\).
To start, the definition of I-additivity of order \(\ell \) applied to the composition candidate \(( {{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{c}}}}}, \rho _{{{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{b}}}}}}\rho _{{{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{c}}}}}} )\) immediately yields the expression (94) for the sum of the terms (93a) over all subsequences \({\textsf {a}}_1\cdots {\textsf {a}}_\ell \) of the underlying string \({{\mathbf {\mathsf{{a}}}}}\).

The sum of the terms (93b) over all subsequences \({\textsf {a}}_1\cdots {\textsf {a}}_\ell \) of the underlying string \({{\mathbf {\mathsf{{a}}}}}\) can be upper bounded as in (95). In step (95a), I have used the hypothesis that F is O-monotone (together with the obvious fact that \({{\mathbf {\mathsf{{b}}}}}_{{\textsf {a}}_1\cdots {\textsf {a}}_\ell }\) is a subsequence of \({{\mathbf {\mathsf{{b}}}}}\)). Step (95b) follows from the fact that the restriction of \( \rho _{{{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{b}}}}}}\) to the string pair \(({\textsf {a}}_1\cdots {\textsf {a}}_\ell , \, {{\mathbf {\mathsf{{b}}}}}_{{\textsf {a}}_1\cdots {\textsf {a}}_\ell })\) is identical to its restriction to the string pair \(({\textsf {a}}_1\cdots {\textsf {a}}_\ell , \, {{\mathbf {\mathsf{{b}}}}})\), because \({{\mathbf {\mathsf{{b}}}}}_{{\textsf {a}}_1\cdots {\textsf {a}}_\ell }\) is the subsequence of \({{\mathbf {\mathsf{{b}}}}}\) consisting of those segments which are in correspondence with one of the segments \({\textsf {a}}_1, \dots , {\textsf {a}}_\ell \). Step (95c) follows again from the hypothesis that F is I-additive of order \(\ell \).

Finally, let me bound the sum of the terms (93c) over all subsequences \({\textsf {a}}_1\cdots {\textsf {a}}_\ell \) of the underlying string \({{\mathbf {\mathsf{{a}}}}}\). To this end, I note that the implication (96) holds for any two subsequences \({\textsf {a}}_1\cdots {\textsf {a}}_\ell \) and \(\widehat{{\textsf {a}}}_1\cdots \widehat{{\textsf {a}}}_\ell \) and their surface correspondent subsequences \({{\mathbf {\mathsf{{b}}}}}_{{\textsf {a}}_1\cdots {\textsf {a}}_\ell }\) and \({{\mathbf {\mathsf{{b}}}}}_{\widehat{{\textsf {a}}}_1\cdots \widehat{{\textsf {a}}}_\ell }\) of \({{\mathbf {\mathsf{{b}}}}}\).

In fact, assume by contradiction that the antecedent holds but the consequent fails. Since the surface correspondent string \({{\mathbf {\mathsf{{b}}}}}_{{\textsf {a}}_1\cdots {\textsf {a}}_\ell }\) has length at least \(\ell \) and since the correspondence relation \(\rho _{{{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{b}}}}}}\) cannot break any underlying segment into two or more surface segments (because it is one-to-one), each underlying segment \({\textsf {a}}_i\) of \({\textsf {a}}_1\cdots {\textsf {a}}_\ell \) must have a surface correspondent in \({{\mathbf {\mathsf{{b}}}}}_{{\textsf {a}}_1\cdots {\textsf {a}}_\ell }\). The hypothesis \({\textsf {a}}_1\cdots {\textsf {a}}_\ell \ne \widehat{{\textsf {a}}}_1\cdots \widehat{{\textsf {a}}}_\ell \) means that there exists at least one segment \({\textsf {a}}_i\) which belongs to \({\textsf {a}}_1\cdots {\textsf {a}}_\ell \) but not to \(\widehat{{\textsf {a}}}_1\cdots \widehat{{\textsf {a}}}_\ell \). Let \({\textsf {b}}\) be the surface correspondent of \({\textsf {a}}_i\) in \({{\mathbf {\mathsf{{b}}}}}_{{\textsf {a}}_1\cdots {\textsf {a}}_\ell }\). Because of the contradictory assumption that the consequent of (96) fails, \({{\mathbf {\mathsf{{b}}}}}_{{\textsf {a}}_1\cdots {\textsf {a}}_\ell } = {{\mathbf {\mathsf{{b}}}}}_{\widehat{{\textsf {a}}}_1\cdots \widehat{{\textsf {a}}}_\ell }\). This means that \({\textsf {b}}\) also belongs to \({{\mathbf {\mathsf{{b}}}}}_{\widehat{{\textsf {a}}}_1\cdots \widehat{{\textsf {a}}}_\ell }\), namely must correspond to some segment \(\widehat{{\textsf {a}}}_j\) of \(\widehat{{\textsf {a}}}_1\cdots \widehat{{\textsf {a}}}_\ell \). Since \({\textsf {a}}_i\) does not belong to \(\widehat{{\textsf {a}}}_1\cdots \widehat{{\textsf {a}}}_\ell \), then \({\textsf {a}}_i\) and \(\widehat{{\textsf {a}}}_j\) must be different. The conclusion that both \(({\textsf {a}}_i, {\textsf {b}})\) and \((\widehat{{\textsf {a}}}_j, {\textsf {b}})\) belong to \(\rho _{{{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{b}}}}}}\) despite the fact that \({\textsf {a}}_i\ne \widehat{{\textsf {a}}}_j\) contradicts the hypothesis that \(\rho _{{{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{b}}}}}}\) does not coalesce any two underlying segments.
Let me now go back to the goal of bounding the sum of the terms (93c) over all subsequences \({\textsf {a}}_1\cdots {\textsf {a}}_\ell \) of the underlying string \({{\mathbf {\mathsf{{a}}}}}\). Since \({\textsf {a}}_1\cdots {\textsf {a}}_\ell \) has length \(\ell \) and since the correspondence relation \(\rho _{{{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{b}}}}}}\) cannot break any underlying segment (because it is one-to-one), the surface correspondent string \({{\mathbf {\mathsf{{b}}}}}_{{\textsf {a}}_1\cdots {\textsf {a}}_\ell }\) has length \(\ell \) or smaller. If \({{\mathbf {\mathsf{{b}}}}}_{{\textsf {a}}_1\cdots {\textsf {a}}_\ell }\) has length smaller than \(\ell \), the corresponding term (93c) is null, because F is I-additive of order \(\ell \) and thus assigns zero violations to candidates whose underlying string is shorter than \(\ell \), as noted at the beginning. The sum can thus be restricted to candidates whose underlying form \({{\mathbf {\mathsf{{b}}}}}_{{\textsf {a}}_1\cdots {\textsf {a}}_\ell }\) has length exactly \(\ell \), as in step (97a). Condition (96) says that the mapping from the subsequences \({\textsf {a}}_1\cdots {\textsf {a}}_\ell \) to the corresponding surface subsequences \({{\mathbf {\mathsf{{b}}}}}_{{\textsf {a}}_1\cdots {\textsf {a}}_\ell }\) (of length \(\ell \)) is an injection, thus guaranteeing step (97b). Step (97c) follows again from the hypothesis that F is I-additive of order \(\ell \).

The FTI\(_{\text {comp}}\) (88) follows by summing the inequality (93) over all subsequences \({\textsf {a}}_1\cdots {\textsf {a}}_\ell \) of length \(\ell \) of the string \({{\mathbf {\mathsf{{a}}}}}\), using the three expressions (94), (95), and (97) for the sums over the three terms (93a), (93b), and (93c). \(\square \)
1.2 A.2 Proof of Proposition 5
-
Proposition 5 Assume that, for any two candidates \(({{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{b}}}}}, \rho _{{{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{b}}}}}})\) and \(({{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{c}}}}}, \rho _{{{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{c}}}}}})\), the candidate set also contains a candidate \(({{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{c}}}}}, \rho _{{{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{c}}}}}})\) such that the FIC \(^{\,\text {HG}}\) repeated in (98) holds for any faithfulness constraint F in the constraint set.
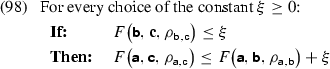
Then, the HG grammar corresponding to any weighting of the constraint set is idempotent, no matter what the markedness constraints look like. \(\square \)
Proof
Suppose that the HG grammar \(G_{\varvec{\theta }}\) corresponding to some weighting \(\varvec{\theta }\) fails at the idempotency implication (32) for some candidate \(({{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{b}}}}}, \rho _{{{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{b}}}}}})\), as stated in (99): \(G_{\varvec{\theta }}\) maps the underlying form \({{\mathbf {\mathsf{{a}}}}}\) to \(({{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{b}}}}}, \rho _{{{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{b}}}}}})\), as required by the antecedent of the idempotency implication; but it fails to map the underlying form \({{\mathbf {\mathsf{{b}}}}}\) to the identity candidate \(({{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{b}}}}}, \mathbb {I}_{{{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{b}}}}}})\), as required by the consequent.

Condition (99b) means that the grammar \(G_{\varvec{\theta }}\) maps the underlying form \({{\mathbf {\mathsf{{b}}}}}\) to a candidate \(({{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{c}}}}}, \rho _{{{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{c}}}}}})\) different from \(({{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{b}}}}}, \mathbb {I}_{{{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{b}}}}}})\). This means that either the two strings \({{\mathbf {\mathsf{{b}}}}}\) and \({{\mathbf {\mathsf{{c}}}}}\) differ or else \({{\mathbf {\mathsf{{b}}}}}\) and \({{\mathbf {\mathsf{{c}}}}}\) coincide but the two correspondence relations \(\rho _{{{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{c}}}}}}\) and \(\mathbb {I}_{{{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{b}}}}}}\) differ. The latter option is impossible, because the candidate \(({{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{b}}}}}, \rho _{{{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{b}}}}}})\) with \(\rho _{{{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{b}}}}}}\ne \mathbb {I}_{{{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{b}}}}}}\) is harmonically bounded by the candidate \(({{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{b}}}}}, \mathbb {I}_{{{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{b}}}}}})\): faithfulness constraints cannot prefer the former candidate, by (8); and markedness constraints cannot distinguish between the two candidates, by (7). The two strings \({{\mathbf {\mathsf{{b}}}}}\) and \({{\mathbf {\mathsf{{c}}}}}\) must therefore differ and condition (99) becomes (100).

By assumption, the two candidates \(({{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{b}}}}}, \rho _{{{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{b}}}}}})\) and \(({{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{c}}}}}, \rho _{{{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{c}}}}}})\) come with a companion candidate \(({{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{c}}}}}, \rho _{{{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{c}}}}}})\). The “if-and-only-if” statement (100) can thus be weakened to the “if” statement (101). In fact, if the grammar \(G_{\varvec{\theta }}\) maps the underlying form \({{\mathbf {\mathsf{{a}}}}}\) to the candidate \(({{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{b}}}}}, \rho _{{{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{b}}}}}})\) as stated in (100a), the weights \(\varvec{\theta }\) prefer this candidate \(({{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{b}}}}}, \rho _{{{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{b}}}}}})\) to the candidate \(({{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{c}}}}}, \rho _{{{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{c}}}}}})\), as stated in (101a). Furthermore, if the grammar \(G_{\varvec{\theta }}\) maps the underlying form \({{\mathbf {\mathsf{{b}}}}}\) to the candidate \(({{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{c}}}}}, \rho _{{{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{c}}}}}})\) as stated in (101b), the weights \(\varvec{\theta }\) prefer this candidate \(({{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{c}}}}}, \rho _{{{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{c}}}}}})\) to the identity candidate \(({{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{b}}}}}, \mathbb {I}_{{{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{b}}}}}})\), as stated in (101b).

Condition (101) can be made explicit as in (102) in terms of the number of constraint violations. These sums run over a generic markedness constraint M with weight \(\theta _M\) and a generic faithfulness constraint F with weight \(\theta _F\). The faithfulness constraints do not appear on the right-hand side of (102b) because \(F({{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{b}}}}}, \mathbb {I}_{{{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{b}}}}}}) = 0\) for every faithfulness constraint F, by (8).

Let the constant \(\xi \) be defined as \(\xi = \sum _{M} \theta _M M({{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{b}}}}}, \mathbb {I}_{{{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{b}}}}}}) - \sum _{M} \theta _M M({{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{c}}}}}, \rho _{{{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{c}}}}}})\). Since markedness constraints are blind to underlying forms by (7), then also \(\xi = \sum _{M} \theta _M M({{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{b}}}}}, \rho _{{{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{b}}}}}}) - \sum _{M} \theta _M M({{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{c}}}}}, \rho _{{{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{c}}}}}})\). Condition (102) thus becomes:

In conclusion, idempotency holds for the HG grammar corresponding to any weighting of the constraint set provided the two conditions (103a) and (103b) can never be both satisfied , no matter the choice of the weights \(\theta _F\) and the constant \(\xi \). In other words, it suffices to assume that, for every two candidates \(( {{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{b}}}}}, \rho _{{{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{b}}}}}} )\) and \(( {{\mathbf {\mathsf{{b}}}}}, \mathbf{c}, \rho _{{{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{c}}}}}} )\), there exists some candidate \(( {{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{c}}}}}, \rho _{{{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{c}}}}}} )\) such that:

To conclude the proof, I need to show that (104) is equivalent to the FIC\(^{\text {HG}}\) (106). To start, let me show that (98) entails (104). In fact, suppose that the antecedent of the implication (104) holds. For every faithfulness constraint F, let \(\xi _F\) be defined as in (105a). The antecedent of the implication (104) can thus be restated as in (105b). I can assume without loss of generality that the weights \(\theta _F\) are all different from zero. The position (105a) thus entails (105c). Since the implication (98) holds by hypothesis, (105c) entails (105d). The consequent of the implication (104) thus follows from (105b) by taking the weighted average of the inequalities (105d) over all faithfulness constraints.

Let me now show that (104) vice versa entails (98). In fact, suppose that the antecedent of the implication (98) holds, namely that \(F({{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{c}}}}}, \rho _{{{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{c}}}}}})\le \xi \). Let me distinguish two cases, depending on whether \(\xi \) is an integer or not. To start, assume that \(\xi \) is not an integer. The assumption \(F({{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{c}}}}}, \rho _{{{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{c}}}}}})\le \xi \) (with the loose inequality) is thus equivalent to the assumption \(F({{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{c}}}}}, \rho _{{{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{c}}}}}}) < \xi \) (with the strict inequality), because constraint violations are integers. The antecedent of the implication (104) thus holds with all the weights set equal to zero but for the weight \(\theta _F\) corresponding to the faithfulness constraint F considered, which is equal to 1. The consequent of the implication (104) must therefore hold as well, which is in turn identical to the consequent of the implication (98) with this special choice of the weights. If instead the antecedent of (98) holds with \(\xi \) equal to an integer, let \(\widehat{\xi } = \xi + 1/2\). By reasoning as above, I conclude that the consequent of the implication (98) holds for \(\widehat{\xi }\). Since constraint violations are integers, the latter entails in turn that the consequent of the implication (98) holds for \(\xi \). \(\square \)
1.3 A.3 Proof of Proposition 12
-
Proposition 12 Assume that, for any two candidates \(({{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{d}}}}}, \rho _{{{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{d}}}}}})\) and \(({{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{d}}}}}, \rho _{{{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{d}}}}}})\) such that \(({{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{d}}}}}, \rho _{{{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{d}}}}}}) \le _{\text {sim}} ({{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{d}}}}}, \rho _{{{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{d}}}}}})\), for every candidate \(({{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{c}}}}}, \rho _{{{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{c}}}}}})\) different from \(({{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{d}}}}}, \rho _{{{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{d}}}}}})\), the candidate set also contains a candidate \(({{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{c}}}}}, \rho _{{{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{c}}}}}})\) different from \(({{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{d}}}}}, \rho _{{{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{d}}}}}})\) such that the FODC \(^{\,\text {HG}}\) repeated in (106) holds for any faithfulness constraint F.
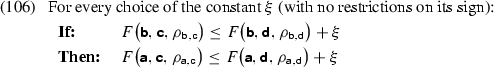
Then, the HG grammar corresponding to any weighting of the constraint set is output-driven relative to the similarity order \(\le _{\text {sim}}\). \(\square \)
Proof
The proof is similar to the proof of Proposition 5 in Appendix A.2. Suppose that the HG grammar \(G_{\varvec{\theta }}\) corresponding to some weighting \(\varvec{\theta }\) fails at the output-drivenness implication (51) for two candidates \(({{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{d}}}}}, \rho _{{{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{d}}}}}})\) and \(({{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{d}}}}}, \rho _{{{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{d}}}}}})\), as stated in (107): the grammar \(G_{\varvec{\theta }}\) maps the underlying form \({{\mathbf {\mathsf{{a}}}}}\) to the candidate \(({{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{b}}}}}, \rho _{{{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{b}}}}}})\) with less internal similarity, as required by the antecedent of (51); but it fails to map the underlying form \({{\mathbf {\mathsf{{b}}}}}\) to the candidate \(({{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{d}}}}}, \rho _{{{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{d}}}}}})\) with more internal similarity, as required by the consequent of (51).

By assumption, the candidate \(({{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{c}}}}}, \rho _{{{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{c}}}}}})\) different from \(({{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{d}}}}}, \rho _{{{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{d}}}}}})\) comes with a companion candidate \(({{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{c}}}}}, \rho _{{{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{c}}}}}})\) different from \(({{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{d}}}}}, \rho _{{{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{d}}}}}})\). The “if-and-only-if” statement (107) can thus be weakened into the “if” statement (108).

Condition (108) can be made explicit as in (109) in terms of the numbers of constraint violations. The sums run over a generic markedness constraint M with weight \(\theta _M\) and a generic faithfulness constraint F with weight \(\theta _F\).

Taking advantage of the fact that markedness constraints are blind to underlying forms by (7), condition (109) can be rewritten as in (110) with the position \(\xi = \sum _{M} \theta _M M({{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{d}}}}}, \rho _{{{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{d}}}}}}) - \sum _{M} \theta _M M({{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{c}}}}}, \rho _{{{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{c}}}}}}) = \sum _{M} \theta _M M({{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{d}}}}}, \rho _{{{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{d}}}}}}) - \sum _{M} \theta _M M({{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{c}}}}}, \rho _{{{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{c}}}}}})\).

In conclusion, output-drivenness holds for the HG grammar corresponding to any constraint weighting provided the two conditions (110a) and (110b) can never be satisfied both, no matter the choice of the weights \(\theta _F\) and the constant \(\xi \). In other words, it suffices to assume that for every candidate \(( {{\mathbf {\mathsf{{b}}}}}, \mathbf{c}, \rho _{{{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{c}}}}}} )\) different from \(({{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{d}}}}}, \rho _{{{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{d}}}}}})\) there exists a candidate \(( {{\mathbf {\mathsf{{a}}}}}, \mathbf{c}, \rho _{{{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{c}}}}}} )\) different from \(({{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{d}}}}}, \rho _{{{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{d}}}}}})\) such that:

To conclude the proof, condition (111) can be shown to be equivalent to the FODC\(^{\text {HG}}\) (106) by reasoning as at the end of the proof of Proposition 5 to show that condition (104) is equivalent to the FIC\(^{\text {HG}}\) (98). \(\square \)
1.4 A.4 Proof of Proposition 13
-
Proposition 13 The two FODC \(^{\, OT}\) implications repeated in (112)
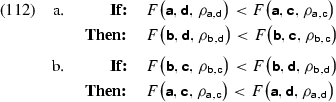
are jointly equivalent to the following condition:
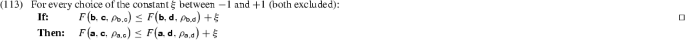
Proof
Let me show that the two FODC\(^{\text {OT}}\) implications (112) jointly entail the implication (113). Thus, assume that the antecedent of the latter implication holds for some \(\xi \). I distinguish two cases, depending on whether \(\xi \) is (strictly) smaller than 0 or not. Let me start with the former case, stated in (114a).

Since \(\xi \) is strictly negative, (114a) entails the strict inequality (114b). The latter in turn coincides with the antecedent of the second FODC\(^{\text {OT}}\) implication (112b), which therefore ensures that its consequent holds as well, repeated in (114c). Since \(\xi \) is larger than \(-1\) and constraint violations are integers, (114c) in turn entails (114d), which is the desired consequent of the implication (113). Note that this reasoning has used only the second FODC\(^{\text {OT}}\) implication (112b).
Consider next the complementary case where the antecedent of the implication (113) holds with a nonnegative \(\xi \), as stated in (115a).

Since \(\xi \) is smaller than \(+1\) and constraint violations are integers, (114a) entails (114b). The latter in turns says that the consequent of the first FODC\(^{\text {OT}}\) implication (112a) fails. The antecedent must therefore fail as well, as stated in (114c). Since \(\xi \) is nonnegative, the latter in turn entails (114d), which is the desired consequent of the implication (113). Note that this reasoning has used only the first FODC\(^{\text {OT}}\) implication (112a).
Next, let me show that condition (113) with \(0< \xi < +1\) in turn entails the first FODC\(^{\text {OT}}\) implication (112a). In fact, suppose that the antecedent of the latter implication holds, namely that \(F ( {{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{d}}}}}, \rho _{{{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{d}}}}}} ) < F({{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{c}}}}}, \rho _{{{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{c}}}}}})\). Since \(\xi \) is smaller than \(+1\) and constraint violations are integers, the latter entails that \(F ( {{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{d}}}}}, \rho _{{{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{d}}}}}} ) + \xi < F ({{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{c}}}}}, \rho _{{{\mathbf {\mathsf{{a}}}}}, {{\mathbf {\mathsf{{b}}}}}} \rho _{{{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{c}}}}}})\). The consequent of the implication (113) thus fails. Its antecedent must therefore fail as well, namely \(F ( {{\mathbf {\mathsf{{b}}}}}, \mathbf{c}, \rho _{{{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{c}}}}}} )\ge F ( {{\mathbf {\mathsf{{b}}}}}, \mathbf{d}, \rho _{{{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{d}}}}}} ) + \xi \). The latter entails that \(F ( {{\mathbf {\mathsf{{b}}}}}, \mathbf{c}, \rho _{{{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{c}}}}}} ) > F ( {{\mathbf {\mathsf{{b}}}}}, \mathbf{d}, \rho _{{{\mathbf {\mathsf{{b}}}}}, {{\mathbf {\mathsf{{d}}}}}} )\), establishing the consequent of the first FODC\(_{\text {comp}}^{\text {OT}}\) implication (112a). An analogous reasoning shows that condition (113) with \(-1< \xi < 0\) entails the second FODC\(_{\text {comp}}^{\text {OT}}\) implication (112b). \(\square \)
Rights and permissions
About this article
Cite this article
Magri, G. Idempotency, Output-Drivenness and the Faithfulness Triangle Inequality: Some Consequences of McCarthy’s (2003) Categoricity Generalization. J of Log Lang and Inf 27, 1–60 (2018). https://doi.org/10.1007/s10849-017-9256-0
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10849-017-9256-0



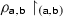 is the set of those pairs
is the set of those pairs 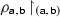 . In fact, the triplet
. In fact, the triplet