Models and solution techniques for production planning problems with increasing byproducts

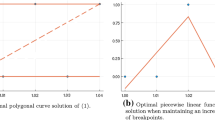
Abstract

We consider a production planning problem where the production process creates a mixture of desirable products and undesirable byproducts. In this production process, at any point in time the fraction of the mixture that is an undesirable byproduct increases monotonically as a function of the cumulative mixture production up to that time. The mathematical formulation of this continuous-time problem is nonconvex. We present a discrete-time mixed-integer nonlinear programming (MINLP) formulation that exploits the increasing nature of the byproduct ratio function. We demonstrate that this new formulation is more accurate than a previously proposed MINLP formulation. We describe three different mixed-integer linear programming (MILP) approximation and relaxation models of this nonconvex MINLP, and we derive modifications that strengthen the linear programming relaxations of these models. We also introduce nonlinear programming formulations to choose piecewise-linear approximations and relaxations of multiple functions that share the same domain and use the same set of break points in the domain. We conclude with computational experiments that demonstrate that the proposed formulation is more accurate than the previous formulation, and that the strengthened MILP approximation and relaxation models can be used to obtain provably near-optimal solutions for large instances of this nonconvex MINLP. Experiments also illustrate the quality of the piecewise-linear approximations produced by our nonlinear programming formulations.

Appendices

Appendix 1

1.1 Production functions

We normalized the range of the total production function so that the cumulative production variable $v$ has takes values in $[0,1]$. We used bounded, concave production functions of the form $f(x) = r_0 + r_1x + r_2x^2$ with $r_2 < 0$. We randomly generated $f(\cdot )$ by choosing $r_0 \sim \hbox {U}(15,25), r_2 \sim \hbox {U}(-50,0)$ and $r_0 + r_1 + r_2 \sim \hbox {U}(-15,0)$. This procedure was repeated to generate independently and identically distributed samples of production functions $f_i(\cdot )$ for each facility $i \in \mathcal {I}$. The family of functions generated by this procedure always ensures that $f(\cdot )$ is concave.

For each product $p \in \mathcal {P}$, we must generate either a monotonically increasing or decreasing function. Additionally, we must ensure that $\sum _{p \in \mathcal {P}}g_{p}(v) = 1, \forall v \in [0,1]$. We simulated such functions by scaling and translating a randomly generated function from a family of functions. One such family of monotonically increasing functions is $\hat{g}(v) = \int \nolimits _0^v u^k(1-u)^k du / \int \nolimits _0^1 u^k (1-u)^k du, k=\{1,2,3\}$. We chose this family of functions because (a) it was rich enough to express productions functions of different kinds, (b) these functions are monotonically increasing, and (c) these functions satisfy $\hat{g}(0) =0$ and $\hat{g}(1) = 1$. We then obtain functions $g_p(v), p \in \mathcal {P}$ by choosing positive real numbers $a_p$ and $b_p$ for $p \in \mathcal {P}$ and then setting

$$\begin{aligned} g_{p}(v) = a_p + (b_p - a_p) \hat{g}(v) \quad \forall p \in \mathcal {P}. \end{aligned}$$

Since the family of generated functions must satisfy $\sum _{p \in \mathcal {P}}g_{p}(v) = 1, \forall v \in [0,1]$, we require

$$\begin{aligned}&\sum _{p \in \mathcal {P}^{+}}a_p + \sum _{p \in \mathcal {P}^{-}}a_p = 1 \end{aligned}$$

(33a)

$$\begin{aligned}&\sum _{p \in \mathcal {P}^{+}}b_p + \sum _{p \in \mathcal {P}^{-}}b_p = 1 \end{aligned}$$

(33b)

where $a_p = g_p(0)$ and $b_p = g_p(1)$. Additionally, we must also ensure that

$$\begin{aligned} a_p&> b_p \quad \forall p \in \mathcal {P}^{+} \end{aligned}$$

(33c)

$$\begin{aligned} a_p&< b_p \quad \forall p \in \mathcal {P}^{-} \end{aligned}$$

(33d)

which makes the useful product ratio functions decreasing and the byproduct ratio function increasing. The following sampling procedure generates product ratio functions which satisfy all the required conditions.

• We sampled $\hat{a}_p \sim \hbox {U}(0.8,1), p \in \mathcal {P}^{+}$ and $\hat{a}_p \sim \hbox {U}(0,0.2), p \in \mathcal {P}^{-}$.

• We normalized the above samples so that $a_p = \frac{\hat{a}_p}{\sum _{p \in \mathcal {P}}\hat{a}_p}, \forall p \in \mathcal {P}$ which ensures that condition (33a) is satisfied.

• Next, we sampled $\hat{b}_p \sim \hbox {U}( 0, \frac{a_p}{2}) \ p \in \mathcal {P}^{+}$ and $\hat{b}_p \sim \hbox {U}( 2a_p,1) \ p \in \mathcal {P}^{-}$ which ensures that conditions (33c) and (33d) are satisfied.

• We normalized the above samples so that $b_p = \frac{\hat{b}_p}{\sum _{p \in \mathcal {P}}\hat{b}_p}, \forall p \in \mathcal {P}$ which ensures that condition (33b) is satisfied.

1.2 Customer demands

We generated increasing demand profiles as follows. For each customer $j \in \mathcal {J}$ and product $p \in \mathcal {P}$, we randomly generated a demand time frame uniformly from start-time between $[1, \frac{T}{3}]$ and end-time between $[\frac{2T}{3},T]$. We generated demands $\{d_{jpt}\} \sim \hbox {U}(0.8,1.2)$ for each time period within the demand time frame, sorted them in increasing order and scaled them by $\frac{\sum _{i \in \mathcal {I}} \sum _{p \in \mathcal {P}^{+}}h_{ip}(1)}{3|\mathcal {J}|}$. Here, $h_{i,p}(1)$ is the cumulative production of each useful product $p \in \mathcal {P}^{+}$ from a facility $i \in \mathcal {I}$. The scaling ensures that the total demand across all customers is roughly a third of the total possible production of useful products over all facilities.

1.3 Costs

We used the following procedure to generate the four different types of costs incurred at each facility. This procedure ensured that at the end of the planning horizon, the total facility opening cost is of the same order as the sum of operating, production and penalty costs. For each customer $j \in \mathcal {J}$, facility $i \in \mathcal {I}$ and product $p \in \mathcal {P}$ during the first time period, we generated operating costs $\beta _{i,p,1} \sim \hbox {U}(0.8, 1.2)$, transportation costs $\gamma _{ijp1} \sim \hbox {U}(0.8, 1.2)$, penalty costs $\delta _{j,p,1} \sim \hbox {U}(16, 24)$ and fixed costs $\alpha _{i1} \sim \frac{\sum _{p \in \mathcal {P}^{+}}h_{ip}(1)}{3|\mathcal {J}|}\hbox {U}(0.8, 1.2)$. We discounted costs at 5  % for subsequent time periods.

Appendix 2: Detailed computational results

We now provide additional details of the computational results described in Sect. 5 of the manuscript. Tables 7, 8, 9 and 10 provide detailed computational results for the experiments performed on the 36 large instances of $PP$-$\mathrm {MINLP2}$. Tables 7 and 8 illustrate the effect of formulation strengthening on the linear programming relaxation gaps of the MILP formulations of $\mathrm {MINLP2}$, and were used to generate the summary statistics displayed in Fig. 9 and Table 3 of the manuscript, respectively. Table 9 shows feasible solution quality of the MILP approximation and relaxation schemes ($\mathrm{PLA}\text {-}\mathrm{SS}, \mathrm{SEC}\text {-}\mathrm{S}$ and $k\text {-}\mathrm{SEC}\text {-}\mathrm{SS}$) by measuring the percentage gap to the best known solution bound of $PP$-$\mathrm {MINLP2}$. Table 10 measures solution bound quality of the MILP relaxation schemes ($\mathrm{SEC}\text {-}\mathrm{S}$ and $k\text {-}\mathrm{SEC}\text {-}\mathrm{SS}$) using the percentage gap to the best known solution feasible solutions of $PP$-$\mathrm {MINLP2}$. Tables 9 and 10 were used to construct summary statistics for Table 4 in the manuscript.

Table 7 Terminal MILP optimality gaps for MILP formulations $\mathrm {MINLP2}$ with and without strengthening while solving 36 large instances of $PP$-$\mathrm {MINLP2}$

Table 8 Linear programming relaxation gaps for MILP formulations of $\mathrm {MINLP2}$ with and without strengthening while solving 36 large instances of $PP$-$\mathrm {MINLP2}$

Table 9 Best found feasible solution statistics for MILP formulations of $\mathrm {MINLP2}$ while solving 36 large instances of $PP$-$\mathrm {MINLP2}$

Table 10 Solution bound statistics for MILP relaxations of $\mathrm {MINLP2}$ while solving 36 large instances of $PP$-$\mathrm {MINLP2}$