The joint replenishment problem with trade credits

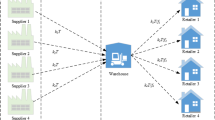
Abstract

It is a widespread financial practice in procurement management for a supplier aiming to attract customers to offer trade credits when customers make inquiries about the sold products. In this paper, we examine the joint replenishment problem considering trade credits (JRP-TC) under the power-of-two (PoT) policy. We formulate a mathematical model and conduct an analysis that reveals insights into the properties of the optimal objective function. From there, we propose an effective search algorithm that obtains the global optimal solution for the JRP-TC under the PoT policy. Our complexity analysis shows that the JRP-TC and the conventional joint replenishment problem under the PoT policy are pseudo-polynomial time solvable.

Appendix

1.1 Proof of Proposition 1

Proof

• (1) The first derivative of ${\phi }_i^{1}(T)$ is

  $$\begin{aligned} \displaystyle \frac{d}{dT}\left( e_i^1T+f_i^1+\frac{g_i^1}{T}\right) =e_i^1-\frac{g_i^1}{T^2}=\displaystyle \frac{D_i(h_i+p_iI_i^d)}{2}-\frac{A_i}{T^2}. \end{aligned}$$

  The second derivative of ${\phi }_i^{1}(T)$ is

  $$\begin{aligned} \displaystyle \frac{d^2}{(dT)^2}\left( e_i^1T+f_i^1+\frac{g_i^1}{T}\right) =\frac{2g_i^1}{T^3}=\displaystyle \frac{2A_i}{T^3} \end{aligned}$$

  which is strictly positive for $T>0$. And the result: $\displaystyle \frac{d^2}{(dT)^2}{\phi }_i^{1}(T) >0$ implies that ${\phi }_i^1(T)$ is a strictly convex function and its minimum occurs at the stationary point $\displaystyle \sqrt{\frac{g_i^1}{e^1_i}}=\sqrt{\frac{2A_i}{D_i(h_i+p_iI_i^d)}}$, i.e. $\displaystyle {\overline{T}}_i^1=\sqrt{\frac{g_i^1}{e^1_i}}=\sqrt{\frac{2A_i}{D_i(h_i+p_iI_i^d)}}$. The first derivative of ${\phi }_i^{2}(T)$ is

  $$\begin{aligned} \displaystyle \frac{d}{dT}\left( e_i^2T+f_i^2+\frac{g_i^2}{T}\right) =e_i^2-\frac{g_i^2}{T^2}=\frac{D_i(h_i+p_iI_i^c)}{2}-\frac{2A_i+p_iD_iM_i^2(I_i^c-I_i^d)}{2T^2}. \end{aligned}$$

  The second derivative of ${\phi }_i^{2}(T)$

  $$\begin{aligned} \displaystyle \frac{d^2}{(dT)^2}\left( e_i^2T+f_i^2+\frac{g_i^2}{T}\right) =\frac{2g_i^2}{T^3}=\frac{2A_i+p_iD_iM_i^2(I_i^c-I_i^d)}{T^3}. \end{aligned}$$

  and it is strictly positive for $T>0$. $\displaystyle \frac{d^2}{(dT)^2} {\phi }_i^{2}(T)>0$ implies that ${\phi }_i^2(T)$ is a convex function and its minimum occurs at the stationary point $\displaystyle \sqrt{\frac{g_i^2}{e^2_i}}=\sqrt{\frac{2A_i+p_iD_i(M_i)^2(I_i^c-I_i^d)}{D_i(h_i+p_iI_i^c)}}$, i.e. $\displaystyle {\overline{T}}_i^2\sqrt{\frac{g_i^2}{e^2_i}}=\sqrt{\frac{2A_i+p_iD_i(M_i)^2(I_i^c-I_i^d)}{D_i(h_i+p_iI_i^c)}}$.

• (2) The long-run average total cost function ${\phi }_i(T)$ is differentiable because

  $$\begin{aligned} \displaystyle \lim _{T\rightarrow (M_i)^{-}}\frac{{\phi }_i(T)-{\phi }_i(M_i)}{T-M_i}= & {} \displaystyle \lim _{T\rightarrow (M_i)^{-}}\frac{e_1^1T+f_i^1+\frac{g_i^1}{T}-e_i^1M_i-f_i^1-\frac{g_i^1}{M_i}}{T-M_i} \\= & {} \displaystyle \lim _{T\rightarrow (M_i)^{-}}\frac{e_1^1\left( T-M_i\right) +g_i^1\left( \frac{1}{T}-\frac{1}{M_i}\right) }{T-M_i} \\= & {} \displaystyle \lim _{T\rightarrow (M_i)^{-}}e_1^1-\frac{g_i^1}{TM_i} \\= & {} \displaystyle e_1^1-\frac{g_i^1}{M_i^2} \\= & {} \displaystyle \frac{-A_i}{M_i^2}+\frac{D_i(h_i+p_iI_i^d)}{2} \end{aligned}$$

  and

  $$\begin{aligned} \displaystyle \lim _{T\rightarrow (M_i)^+}\frac{{\phi }_i(T)-{\phi }_i(M_i)}{T-M_i}= & {} \displaystyle \lim _{T\rightarrow (M_i)^+}\frac{e_i^2T+f_i^2+\frac{g_i^2}{T}-e_i^1M_i-f_i^1-\frac{g_i^1}{M_i}}{T-M_i}\\= & {} \displaystyle \lim _{T\rightarrow (M_i)^+}\frac{e_i^2T-e_i^1M_i}{T-M_i}+\frac{f_i^2-f_i^1}{T-M_i}+\frac{\frac{g_i^2}{T}-\frac{g_i^1}{M_i}}{T-M_i}\\= & {} \displaystyle \lim _{T\rightarrow (M_i)^+}\frac{D_ih_i}{2}-\frac{A_i}{TM_i}+\frac{D_ip_i(I_i^cT-I_i^dM_i)}{2(T-M_i)}\\&\displaystyle +\frac{D_ip_iM_i(I_i^d-I_i^c)}{T-M_i}+\frac{D_ip_iM_i^2(I_i^d-I_i^c)}{2T(T-M_i)}\\= & {} \displaystyle \lim _{T\rightarrow (M_i)^+}\frac{D_ih_i}{2}-\frac{A_i}{TM_i}+\frac{D_ip_i\left( I_i^dM_i+I_i^c\left( T-M_i\right) \right) }{2T}\\= & {} \displaystyle \frac{D_i(h_i+p_iI_i^d)}{2}-\frac{A_i}{M_i^2}. \end{aligned}$$

  The long-run average total cost function ${\phi }_i(T)$ is strictly convex since $\displaystyle \frac{d}{dT}{\phi }_i(T)$ is strictly increasing from

  • $\displaystyle \frac{d}{dT}{\phi }_i(T)=\displaystyle \frac{d}{dT}{\phi }_i^1(T)$ is strictly increasing on $\left( 0,M_i\right]$;

  • $\displaystyle \frac{d}{dT}{\phi }_i(T)=\displaystyle \frac{d}{dT}{\phi }_i^2(T)$ is strictly increasing on $\left[ M_i,\infty \right)$;

  • $\displaystyle \frac{d}{dT}{\phi }_i^1(M_i)=\frac{d}{dT}{\phi }_i^2(M_i)$.

• (3) The function ${\phi }_i(T)$ is strictly convex, hence it has only one stationary point. We only need to verify that

  $$\begin{aligned} \left. \frac{d}{dT}{\phi }_i(T)\right| _{T={\overline{T}}_i}=0. \end{aligned}$$

  There are three cases: ${\overline{T}}_i^1< M_i$, ${\overline{T}}_i^1 = M_i$ and ${\overline{T}}_i^1>M_i$.

  • (a) If ${\overline{T}}_i^1< M_i$, then ${\overline{T}}_i={\overline{T}}_i^1$. Since

    $$\begin{aligned} \displaystyle \frac{d}{dT}{\phi }_i(T)=\left\{ \begin{array}{ll} \displaystyle \frac{d}{dT}{\phi }_i^1(T) &{}\hbox { if }T<M_i\\ \displaystyle \frac{d}{dT}{\phi }_i^2(T) &{}\hbox { if }T>M_i\\ \end{array} \right. , \end{aligned}$$

    we obtain

    $$\begin{aligned} \left. \frac{d}{dT}{\phi }_i(T)\right| _{T={\overline{T}}_i}=\left. \frac{d}{dT}{\phi }_i^1(T)\right| _{T={\overline{T}}_i}=\left. \frac{d}{dT}{\phi }_i^1(T)\right| _{T={\overline{T}}_i^1}=0. \end{aligned}$$

  • (b) If ${\overline{T}}_i^1= M_i$, then ${\overline{T}}_i={\overline{T}}_i^1=M_i$. Since

    $$\begin{aligned} \left. \displaystyle \frac{d}{dT}{\phi }_i(T)\right| _{T={\overline{T}}_i^1}=\frac{-A_i}{M_i^2}+\frac{D_i(h_i+p_iI_i^d)}{2}=\left. \frac{d}{dT}{\phi }_i^1(T)\right| _{T={\overline{T}}_i^1}, \end{aligned}$$

    we obtain

    $$\begin{aligned} \left. \frac{d}{dT}{\phi }_i(T)\right| _{T={\overline{T}}_i}=\left. \frac{d}{dT}{\phi }_i^1(T)\right| _{T={\overline{T}}_i^1}=0. \end{aligned}$$

  • (c) If ${\overline{T}}_i^1 > M_i$, then ${\overline{T}}_i={\overline{T}}_i^2$. Since

    $$\begin{aligned} \displaystyle \frac{d}{dT}{\phi }_i(T)=\left\{ \begin{array}{ll} \displaystyle \frac{d}{dT}{\phi }_i^1(T) &{}\hbox { if }T<M_i\\ \displaystyle \frac{d}{dT}{\phi }_i^2(T) &{}\hbox { if }T>M_i\\ \end{array} \right. , \end{aligned}$$

    we obtain

    $$\begin{aligned} \left. \frac{d}{dT}{\phi }_i(T)\right| _{T={\overline{T}}_i}=\left. \frac{d}{dT}{\phi }_i^2(T)\right| _{T={\overline{T}}_i}=\left. \frac{d}{dT}{\phi }_i^2(T)\right| _{T={\overline{T}}_i^2}=0. \end{aligned}$$

$\square$

1.2 Lemma 1 and its proof

Lemma 1

Suppose $B_i^1$ is satisfied

$$\begin{aligned} {\phi }_i(B_i^1)-{\phi }_i(2B_i^1)=0. \end{aligned}$$

(27)

Then

• (1) the solution $B_i^1$ is unique;

• (2) there exists a $\delta >0$ such that

  $$\begin{aligned} \frac{d}{dB} {\phi }_i(B)<0\hbox { and } \frac{d}{dB} {\phi }_i(2B)>0 \end{aligned}$$

  $\forall B\in (B^1_i-\delta , B^1_i+\delta )$;

• (3) the inequality holds:

  $$\begin{aligned} {\phi }_i(B) < {\phi }_i(2B)\hbox { for }B> B_i^1; \end{aligned}$$

  (28)

• (4) the inequality holds:

  $$\begin{aligned} {\phi }_i(B) > {\phi }_i(2B)\hbox { for }B < B_i^1. \end{aligned}$$

  (29)

Proof

• (1) Suppose ${\overline{T}}_i$ is the minimal solution of ${\phi }_i(T)$ on $(0,\infty )$. Let $G(B)={\phi }_i(B)-{\phi }_i(2B)$. Since the minimum of ${\phi }_i(2T)$ occurs at $\displaystyle \frac{{\overline{T}}_i}{2}$, we have

  $$\begin{aligned} {\phi }_i(2{\overline{T}}_i)>{\phi }_i\left( 2\cdot \frac{{\overline{T}}_i}{2}\right) . \end{aligned}$$

  Hence

  $$\begin{aligned} G\left( {\overline{T}}_i\right) ={\phi }_i\left( {\overline{T}}_i\right) -{\phi }_i\left( 2{\overline{T}}_i\right) ={\phi }_i\left( 2\cdot \frac{{\overline{T}}_i}{2}\right) -{\phi }_i\left( 2{\overline{T}}_i\right) <0. \end{aligned}$$

  On the other hand, since the minimum of ${\phi }_i(T)$ occurs on ${\overline{T}}_i$,

  $$\begin{aligned} {\phi }_i\left( \frac{{\overline{T}}_i}{2}\right) >{\phi }_i\left( {\overline{T}}_i\right) . \end{aligned}$$

  Hence

  $$\begin{aligned} G\left( \frac{{\overline{T}}_i}{2}\right) ={\phi }_i\left( \frac{{\overline{T}}_i}{2}\right) -{\phi }_i\left( {\overline{T}}_i\right) ={\phi }_i\left( \frac{{\overline{T}}_i}{2}\right) -{\phi }_i\left( {\overline{T}}_i\right) >0. \end{aligned}$$

  Since $\displaystyle G\left( {\overline{T}}_i\right) \cdot G\left( \frac{{\overline{T}}_i}{2}\right) <0$, and G(T) is continuous on $\displaystyle \left[ \frac{{\overline{T}}_i}{2}, {\overline{T}}_i\right]$, by Intermediate Value Theorem, there exists a $\displaystyle \overline{{\overline{T}}}\in \displaystyle \left( \frac{{\overline{T}}_i}{2}, {\overline{T}}_i\right)$ such that $G(\overline{{\overline{T}}})=0$. Now, we are going to prove the uniqueness of $B_{i}^{1}$. Suppose on the contrary.

  • If there would exist $\displaystyle T^0\in \left( 0, \displaystyle \frac{{\overline{T}}}{2}\right]$ such that $G(T^0)={\phi }_i(T^0)-{\phi }_i(2T^0)=0$. Since $T^0\in \left( 0, \displaystyle \frac{{\bar{T}}}{2}\right]$, we can obtain $T^0 < 2T^0\le {\overline{T}}$. Then $T^0 < 2T^0\le {\overline{T}}$ and ${\phi }_i(T^0)={\phi }_i(2T^0)$ contradicts to that ${\phi }_i(T)$ is an strictly decreasing function on $\left( 0, {\overline{T}}\right]$.

  • If there would exist $T^0\in \left[ {\overline{T}}, \infty \right)$ such that ${\phi }_i(T^0)-{\phi }_i(2T^0)=0$. Since $T^0\in [{\overline{T}}, \infty )$, we obtain ${\overline{T}}\le T^0< 2T^0$. Then ${\overline{T}}\le T^0< 2T^0$ and ${\phi }_i(T^0)={\phi }_i(2T^0)$ contradict to that ${\phi }_i(T)$ is strictly increasing function on $[{\overline{T}}, \infty )$.

  Therefore, there are no $T\in \displaystyle \left( 0,\frac{{\overline{T}}_i}{2}\right) \cup \left( {\overline{T}}_i,\infty \right)$ such that $G(T)=0$.

• (2) Next, we would prove that $\exists \delta >0, \forall B\in \left( \overline{{\overline{T}}}-\delta , \overline{{\overline{T}}}+\delta \right)$ such that

  $$\begin{aligned} {\phi }_i'(B)<0 \hbox { and } {\phi }_i'(2B)>0 \end{aligned}$$

  (30)

  • (a) $\displaystyle \overline{{\overline{T}}}< {\overline{T}}_i$ implies ${\phi }_i'\left( \overline{{\overline{T}}}\right) <0$. Because ${\phi }_i(T)$ is convex, if we choose $\displaystyle \delta _1={\overline{T}}_i-\overline{{\overline{T}}}$, then $\displaystyle B\in \left( \overline{{\overline{T}}}-\delta _1, \overline{{\overline{T}}}+\delta _1\right)$ implies that $\displaystyle {\phi }_i'(B)<0$.

  • (b) $\displaystyle \frac{{\overline{T}}_i}{2}< \overline{{\overline{T}}}$ implies ${\phi }_i'(2\overline{{\overline{T}}})>0$. Because ${\phi }_i(T)$ is convex, if we choose $\displaystyle \delta _2=\overline{{\overline{T}}}-\frac{{\overline{T}}_i}{2}$, then $\displaystyle B\in \left( \overline{{\overline{T}}}-\delta _2, \overline{{\overline{T}}}+\delta _2\right)$ implies that $\displaystyle 2{\phi }_i'(2B)>0$

  Let $\delta =\min \left\{ \delta _1, \delta _2\right\}$, then we obtain (30).

• (3), (4) By (2), there exists a $\delta >0$ such that the derivative

  $$\begin{aligned} \displaystyle \frac{d}{dB}\left( {\phi }_i(B)-{\phi }_i(2B)\right) \end{aligned}$$

  is negative for all $B\in (B_i^1-\delta ,B_i^1+\delta )$. Hence, if $B\in (B_i^1,B_i^1+\delta )$, then ${\phi }_i(B)-{\phi }_i(2B)<0$. If $B\in (B_i^1-\delta ,B_i^1)$, then ${\phi }_i(B)-{\phi }_i(2B)>0$. Moreover, with the uniqueness of $B_i^1$, the sign of ${\phi }_i(B)-{\phi }_i(2B)$ will never change again. Therefore, we obtain that

  $$\begin{aligned} {\phi }_i(B)< {\phi }_i(2B)\hbox { if }B> B_i^1 \\ {\phi }_i(B) > {\phi }_i(2B)\hbox { if }B < B_i^1. \end{aligned}$$

$\square$

1.3 Proof of Theorem 2

Proof

With the uniqueness of $B_i^1$, the sign of ${\phi }_i(B)-{\phi }_i(2B)$ will never change again. Therefore, we obtain that

$$\begin{aligned} {\phi }_i(B)< {\phi }_i(2B)\hbox { if }B> B_i^1 \\ {\phi }_i(B) > {\phi }_i(2B)\hbox { if }B < B_i^1. \end{aligned}$$

Then

$$\begin{aligned} \begin{array}{l} \min \{{\phi }_i(B),{\phi }_i(2B) \}= \left\{ \begin{array}{ll} {\phi }_i(B) &{} \hbox { if }B> B_i^1\\ {\phi }_i(2B) &{} \hbox { if }B < B_i^1. \end{array} \right. \\ \end{array} \end{aligned}$$

Moreover, because of $B_i^{2^j}\triangleq \displaystyle \frac{B_i^1}{2^j}$ for $j\in \{1,2,\ldots \}$ and ${\phi }_i(B_i^1)-{\phi }_i(2B_i^1)=0$, we obtain that ${\phi }_i(2^{j}B_i^{2^j})={\phi }_i(2^{j+1}B_i^{2^j})$ for $j\in \{1,2,\ldots \}$. From

$$\begin{aligned} {\phi }_i(B) < {\phi }_i(2B)\hbox { if }B> B_i^1 \end{aligned}$$

and

$$\begin{aligned} {\phi }_i(B) > {\phi }_i(2B)\hbox { if }B < B_i^1, \end{aligned}$$

we obtain

$$\begin{aligned} {\phi }_i(2^{j}B)< {\phi }_i(2^{j+1}B)\hbox { if } 2^{j}B> B_i^{1} \end{aligned}$$

and

$$\begin{aligned} {\phi }_i(2^{j}B)> {\phi }_i(2^{j+1}B)\hbox { if } 2^{j}B< B_i^{1}. \end{aligned}$$

Hence if $B> B_i^{2^{j}},\forall j\in \{1,2,\ldots \}$, then

$$\begin{aligned} {\phi }_i(2^{j}B)< {\phi }_i(2^{j+1}B); \end{aligned}$$

if $B< B_i^{2^{j}},\forall j\in \{1,2,\ldots \}$, then

$$\begin{aligned} {\phi }_i(2^{j}B)> {\phi }_i(2^{j+1}B). \end{aligned}$$

• (1) Since $B>B_i^1$ implies that $B>B_i^{2^l}$ for all $l\in \{0,1,\ldots \}$, we obtain the following inequalities

  $$\begin{aligned} {\phi }_i(B)< {\phi }_i(2B)< \cdots<{\phi }_i(2^{l}B)<{\phi }_i(2^{l+1}B)<\cdots . \end{aligned}$$

  Hence

  $$\begin{aligned} \min _{k_i}{\phi }_i(k_iB)={\phi }_i(B). \end{aligned}$$

• (2) Since $B_i^{2^{j}}< B < B_i^{2^{j-1}}$ implies that

  $$\begin{aligned} \cdots<B_i^{2^{j+1}}<B_i^{2^{j}}<B< B_i^{2^{j-1}}<B_i^{2^{j-2}}<\cdots <B_i^{1}, \end{aligned}$$

  we obtain the following inequalities

  $$\begin{aligned} {\phi }_i(2^{j}B)< {\phi }_i(2^{j+1}B) < \cdots \end{aligned}$$

  and

  $$\begin{aligned} {\phi }_i(2^{j}B)< {\phi }_i(2^{j-1}B)< \cdots <{\phi }_i(B). \end{aligned}$$

  Hence

  $$\begin{aligned} \min _{k_i}{\phi }_i(k_iB)={\phi }_i\left( 2^{j}B\right) . \end{aligned}$$

• (3) From (1), if $B>B_i^1$, then $\displaystyle \min _{k_i}{\phi }_i(k_iB)={\phi }_i(B)$ is a strictly convex function on $\left( B_i^1,\infty \right)$. From (2), if $B_i^{2^{j}}< B < B_i^{2^{j-1}}$ for some $j\in \{1,2,\ldots \}$, then $\displaystyle \min _{k_i}{\phi }_i(k_iB)={\phi }_i\left( 2^{j}B\right)$ is a strictly convex function on $\left( B_i^{2^{j}}, B_i^{2^{j-1}}\right)$. Hence $\min _{k_i}{\phi }_i(k_iB)$ is piecewise-convex on $(0,\infty )$.

$\square$

1.4 Lemma 2 and its proof

Lemma 2

• 1. If ${\overline{g}}_i\le 0$, then ${\overline{f}}_i-\sqrt{\left( {\overline{f}}_i\right) ^2-2{\overline{e}}_i\,{\overline{g}}_i} \le 0.$

• 2. $\displaystyle \frac{{\overline{f}}_i-\sqrt{\left( {\overline{f}}_i\right) ^2-2{\overline{e}}_i\,{\overline{g}}_i}}{2{\overline{e}}_i}\notin \left[ \frac{M_i}{2},M_i\right] .$

Proof

• 1. The values of ${\overline{e}}_i$ and ${\overline{f}}_i$ are strictly positive since

  $$\begin{aligned} {\overline{e}}_i=2e_i^2-e_i^1=D_i(h_i+p_iI_c)-\frac{D_i(h_i+p_iI_d)}{2} =\frac{D_i(h_i-p_iI_d+2p_iI_c)}{2}>0 \end{aligned}$$

  and

  $$\begin{aligned} {\overline{f}}_i=f_i^1-f_i^2=-p_iD_iI_dM_i+p_iD_iI_cM_i=p_iD_iM_i(I_c-I_d)>0. \end{aligned}$$

  Hence

  $$\begin{aligned}&{\overline{g}}_i\le 0 \\&\quad \Rightarrow ({\overline{f}}_i)^2-2{\overline{e}}_i\,{\overline{g}}_i\ge ({\overline{f}}_i)^2\\&\quad \Rightarrow \sqrt{({\overline{f}}_i)^2-2{\overline{e}}_i\,{\overline{g}}_i} \ge \sqrt{({\overline{f}}_i)^2}=|{\overline{f}}_i|={\overline{f}}_i\\&\quad \Rightarrow {\overline{f}}_i-\sqrt{({\overline{f}}_i)^2-2{\overline{e}}_i\,{\overline{g}}_i}\le 0.\\ \end{aligned}$$

• 2. By (1), we can ignore the case: ${\overline{g}}_i \le 0$. Assume ${\overline{g}}_i > 0$. Since

  $$\begin{aligned} x-\sqrt{x^2-yz}<\sqrt{yz} \end{aligned}$$

  holds for $x>0$, $y>0$, $z>0$, $x^2-yz>0$, we obtain

  $$\begin{aligned} \displaystyle \frac{{\overline{f}}_i-\sqrt{({\overline{f}}_i)^2-2{\overline{e}}_i\,{\overline{g}}_i}}{2{\overline{e}}_i}< \displaystyle \frac{\sqrt{2{\overline{e}}_i\,{\overline{g}}_i}}{2{\overline{e}}_i} =\sqrt{\frac{{\overline{g}}_i}{2{\overline{e}}_i}}. \end{aligned}$$

  Moreover, the inequality $\displaystyle \sqrt{\frac{{\overline{g}}_i}{2{\overline{e}}_i}}<\frac{M_i}{2}$ holds because

  $$\begin{aligned}&\frac{{\overline{g}}_i}{2{\overline{e}}_i}-\frac{(M_i)^2}{4}=\frac{-4A_i-(M_i)^2h_iD_i-(M_i)^2D_ip_iI_i^d}{8{\overline{e}}_i}<0. \end{aligned}$$

  Hence $\displaystyle \frac{{\overline{f}}_i-\sqrt{({\overline{f}}_i)^2-2{\overline{e}}_i\,{\overline{g}}_i}}{2{\overline{e}}_i} <\frac{M_i}{2}$ and

  $$\begin{aligned} \displaystyle \frac{{\overline{f}}_i-\sqrt{({\overline{f}}_i)^2-2{\overline{e}}_i\,{\overline{g}}_i}}{2{\overline{e}}_i}\notin \left[ \frac{M_i}{2},M_i\right] . \end{aligned}$$

$\square$

1.5 Proof of Proposition 3

Proof

• (1) Suppose $\displaystyle T_i^{\alpha }\in \left( 0,\frac{M_i}{2}\right]$. Then

  $$\begin{aligned}&{\phi }_i(T_i^{\alpha })-{\phi }_i\left( 2T_i^{\alpha }\right) \\&\quad ={\phi }_i^1(T_i^{\alpha })-{\phi }_i^1\left( 2T_i^{\alpha }\right) \left( \because T_i^{\alpha }\le \frac{M_i}{2}\Rightarrow T_i^{\alpha }<M_i\right) \\&\quad =e_i^1T_i^{\alpha }+f_i^1+\frac{g_i^1}{T_i^{\alpha }}-2e_i^1T_i^{\alpha }-f_i^1-\frac{g_i^1}{2T_i^{\alpha }}\\&\quad =-e_i^1T_i^{\alpha }+\frac{g_i^1}{T_i^{\alpha }}-\frac{g_i^1}{2T_i^{\alpha }}\\&\quad =-e_i^1\sqrt{\frac{g_i^1}{2e_i^1}}+g_i^1\sqrt{\frac{2e_i^1}{g_i^1}}-\frac{g_i^1}{2}\sqrt{\frac{2e_i^1}{g_i^1}}=0\\ \end{aligned}$$

• (2) Suppose $T_i^{\beta }\in \left[ \frac{M_i}{2},M_i\right]$. Then

  $$\begin{aligned}&{\phi }_i(T_i^{\beta })-{\phi }_i\left( 2T_i^{\beta }\right) \\&\quad ={\phi }_i^1(T_i^{\beta })-{\phi }_i^2\left( 2T_i^{\beta }\right) \left( \because \frac{M_i}{2}\le T_i^{\beta }\le M_i\right) \\&\quad =e_i^1T_i^{\beta }+f_i^1+\frac{g_i^1}{T_i^{\beta }}-2e_i^2T_i^{\beta }-f_i^2-\frac{g_i^2}{2T_i^{\beta }}\\&\quad =T_i^{\beta }\left( e_i^1-2e_i^2\right) +\left( f_i^1-f_i^2\right) +\left( \frac{2g_i^1-g_i^2}{2T_i^{\beta }}\right) \\&\quad =-{\overline{e}}_iT_i^{\beta }+{\overline{f}}_i+\left( \frac{-{\overline{g}}_i}{2T_i^{\beta }}\right) =0 \end{aligned}$$

• (3) Suppose $T_i^{\gamma }\ge M_i$. Then

  $$\begin{aligned}&{\phi }_i(T_i^{\gamma })-{\phi }_i\left( 2T_i^{\gamma }\right) \\&\quad ={\phi }_i^2(T_i^{\gamma })-{\phi }_i^2\left( 2T_i^{\gamma }\right) \left( \because T_i^{\gamma }\ge M_i\Rightarrow T_i^{\gamma }>\frac{M_i}{2}\right) \\&\quad =e_i^2T_i^{\gamma }+f_i^2+\frac{g_i^2}{T_i^{\gamma }}-2e_i^2T_i^{\gamma }-f_i^2-\frac{g_i^2}{2T_i^{\gamma }}\\&\quad =-e_i^2T_i^{\gamma }+\frac{g_i^2}{T_i^{\gamma }}-\frac{g_i^2}{2T_i^{\gamma }}\\&\quad =-e_i^2\sqrt{\frac{g_i^2}{2e_i^2}}+g_i^2\sqrt{\frac{2e_i^2}{g_i^2}}-\frac{g_i^1}{2}\sqrt{\frac{2e_i^1}{g_i^1}}\\&\quad =-\sqrt{\frac{e_i^2g_i^2}{2}}+2\sqrt{\frac{e_i^2g_i^2}{2}}-\sqrt{\frac{e_i^2g_i^2}{2}}\\&\quad =0 \end{aligned}$$

• (4) If one of the conditions $\displaystyle T_i^{\alpha }\in \left( 0,\frac{M_i}{2}\right]$, $\displaystyle T_i^{\beta }\in \left[ \frac{M_i}{2},M_i\right]$, $\displaystyle T_i^{\gamma }\ge M_i$ holds, then, from (1)–(3), there are at least two of $T_i^{\alpha }$, $T_i^{\beta }$, $T_i^{\gamma }$ are $B^1_i$ which contradicts to the uniqueness of $B^1_{i}$ in Proposition 1.

• (5) From (1)–(4), we can obtain the result.

$\square$

1.6 Proof of Proposition 4

Proof

By the definition of ${\overline{J}}_1,{\overline{J}}_2,\ldots ,{\overline{J}}_{n-1}$, we have

$$\begin{aligned} B_{\tau _{n}}^1\in \left[ B_{i}^{2^{{\overline{J}}_i+1}}, B_{i}^{2^{{\overline{J}}_i}}\right) , \forall i\in \{1,2,\ldots ,n-1\} \end{aligned}$$

(31)

After sorting the set $\left\{ B_{\tau _n}^{1},B_{{n-1}}^{2^{{\overline{J}}_{n-1}}}, B_{{n-2}}^{2^{{\overline{J}}_{n-2}}}, \cdots , B_{{1}}^{2^{{\overline{J}}_{1}}}\right\}$, we obtain a bijective function $\sigma :\Lambda \rightarrow \Lambda$ such that

$$\begin{aligned} B_{\sigma _{n}}^{2^{{\overline{J}}_{\sigma _{n}}}} \le B_{\sigma _{n-1}}^{2^{{\overline{J}}_{\sigma _{n-1}}}} \le B_{\sigma _{n-2}}^{2^{{\overline{J}}_{\sigma _{n-2}}}} \le \cdots \le B_{\sigma _{1}}^{2^{{\overline{J}}_{\sigma _{1}}}}. \end{aligned}$$

(32)

Note that $B_{\sigma _{n}}^{2^{{\overline{J}}_{\sigma _{n}}}}=B_{\tau _n}^{1}$. For short notation, we define

$$\begin{aligned} {\widetilde{B}}_i=B_{\sigma _{i}}^{2^{{\overline{J}}_{\sigma _{i}}}},\forall i\in \Lambda . \end{aligned}$$

Then combining (31) with (32), we obtain

$$\begin{aligned} \frac{{\widetilde{B}}_1}{2} \le {\widetilde{B}}_n \le {\widetilde{B}}_{n-1} \le {\widetilde{B}}_{n-2} \le \cdots \le {\widetilde{B}}_{1}. \end{aligned}$$

(33)

Since $B_{\tau _n}^{1}$ is smaller than the junction points $B_{\sigma _{i}}^{2^{j}}$ for all $i\in \{1,2,\ldots n-1\}$ and $j\in \{0,1,\ldots ,{\overline{J}}_{\sigma _{i}}\}$, we obtain $w_{{\bar{l}}}=B_{\tau _n}^{1}={\widetilde{B}}_n$ and $w_{{\bar{l}}+1}=\displaystyle \frac{{\widetilde{B}}_1}{2}$ where

$$\begin{aligned} \displaystyle {\bar{l}}=1+\sum _{i=1}^{n-1}(1+{\overline{J}}_{\sigma _{i}})=n+\sum _{i=1}^{n-1}{\overline{J}}_{\sigma _{i}}=n-1+\sum _{i=1}^{n}{\overline{J}}_{\sigma _{i}}=n-1+\sum _{i=1}^{n}{\overline{J}}_{i}. \end{aligned}$$

Moreover, the inequalities (33) can be extended to

$$\begin{aligned} \frac{{\widetilde{B}}_1}{2^{l'+1}} \le \frac{{\widetilde{B}}_{n}}{2^{l'}} \le \frac{{\widetilde{B}}_{n-1}}{2^{l'}} \le \frac{{\widetilde{B}}_{n-2}}{2^{l'}} \le \cdots \le \frac{{\widetilde{B}}_{1}}{2^{l'}}, \forall l'\in \{1,2,\ldots \}. \end{aligned}$$

(34)

Since $w_{{\bar{l}}+1}=\displaystyle \frac{{\widetilde{B}}_1}{2}$, we have $w_{{\bar{l}}+(l'-1)n+i}=\displaystyle \frac{{\widetilde{B}}_{i}}{2^{l'}}$ and $w_{{\overline{l}}}=2w_{{\overline{l}}+n}$. Suppose $l\ge {\overline{l}}+1$, then there exist $l'\in \{1,2,\ldots \}$ and $i\in \Lambda$ such that $l={\overline{l}}+(l'-1)n+i$. The equalities

$$\begin{aligned} w_{l}=w_{{\overline{l}}+(l'-1)n+i}=\displaystyle \frac{{\widetilde{B}}_{i}}{2^{l'}}=2\frac{{\widetilde{B}}_{i}}{2^{l'+1}}=2w_{{\overline{l}}+l'n+i}=2w_{l+n}. \end{aligned}$$

hold. Therefore, $w_{l}=2w_{l+n}$ hold for all $l\ge {\overline{l}}$.

• (i) Suppose $B\in [w_{{\bar{l}}+(l'-1)n+i+1},w_{{\bar{l}}+(l'-1)n+i})$ for some $l'\in \{1,2,\ldots \}$ and $i\ne n$. Then $\displaystyle B\in \left[ \frac{{\widetilde{B}}_{i+1}}{2^{l'}},\frac{{\widetilde{B}}_{i}}{2^{l'}}\right)$ and $2^{l'} B\in \left[ {\widetilde{B}}_{i+1},{\widetilde{B}}_{i}\right)$.

  • Given $r\in \{1,2,\ldots ,i\}$. Then $\displaystyle 2^{l'}B\in \left[ \frac{{\widetilde{B}}_{r}}{2},{\widetilde{B}}_{r}\right)$ holds, since

    $$\begin{aligned} \frac{{\widetilde{B}}_{r}}{2}\le \cdots \le \frac{{\widetilde{B}}_{1}}{2}\le {\widetilde{B}}_{n}\le \cdots \le {\widetilde{B}}_{i+1}\le {\widetilde{B}}_{i} \le {\widetilde{B}}_{r}. \end{aligned}$$

    Moreover,

    $$\begin{aligned}&\displaystyle 2^{l'}B\in \left[ \frac{{\widetilde{B}}_{r}}{2},{\widetilde{B}}_{r}\right) \Rightarrow B\in \left[ \frac{{\widetilde{B}}_{r}}{2^{l'+1}},\frac{{\widetilde{B}}_{r}}{2^{l'}}\right) \Rightarrow \left\{ \begin{array}{ll} B\in \left[ B_{\sigma _{r}}^{2^{{\overline{J}}_{\sigma _{r}}+l'+1}},B_{\sigma _{r}}^{2^{{\overline{J}}_{\sigma _{r}}+l'}}\right) \\ \displaystyle \frac{B}{2}\in \left[ B_{\sigma _{r}}^{2^{{\overline{J}}_{\sigma _{r}}+l'+2}},B_{\sigma _{r}}^{2^{{\overline{J}}_{\sigma _{r}}+l'+1}}\right) \\ \end{array} \right. \\&\quad \Rightarrow \left\{ \begin{array}{ll} \displaystyle {\overline{k}}_{\sigma _r}(B)={2^{{\overline{J}}_{\sigma _{r}}+l'+1}}\\ \displaystyle {\overline{k}}_{\sigma _r}\left( \frac{B}{2}\right) ={2^{{\overline{J}}_{\sigma _{r}}+l'+2}}\\ \end{array} \right. \Rightarrow {\overline{k}}_{\sigma _r}(B)=\frac{1}{2}{\overline{k}}_{\sigma _r}\left( \frac{B}{2}\right) . \end{aligned}$$

  • Given $r\in \{i+1,i+2,\ldots ,n\}$. Then $2^{l'}B\in \left[ {\widetilde{B}}_{r},2{\widetilde{B}}_{r},\right)$ holds, since

    $$\begin{aligned} {\widetilde{B}}_{r} \le {\widetilde{B}}_{i+1}\le {\widetilde{B}}_{i} \le {\widetilde{B}}_{1} \le 2{\widetilde{B}}_{n} \le 2{\widetilde{B}}_{r}. \end{aligned}$$

    Moreover,

    $$\begin{aligned}&\displaystyle 2^{l'}B\in \left[ {\widetilde{B}}_{r},2{\widetilde{B}}_{r}\right) \Rightarrow B\in \left[ \frac{{\widetilde{B}}_{r}}{2^{l'}},\frac{{\widetilde{B}}_{r}}{2^{l'-1}}\right) \Rightarrow \left\{ \begin{array}{ll} B\in \left[ B_{\sigma _{r}}^{2^{{\overline{J}}_{\sigma _{r}}+l'}},B_{\sigma _{r}}^{2^{{\overline{J}}_{\sigma _{r}}+l'-1}}\right) \\ \displaystyle \frac{B}{2}\in \left[ B_{\sigma _{r}}^{2^{{\overline{J}}_{\sigma _{r}}+l'+1}},B_{\sigma _{r}}^{2^{{\overline{J}}_{\sigma _{r}}+l'}}\right) \\ \end{array} \right. \\&\quad \Rightarrow \left\{ \begin{array}{ll} \displaystyle {\overline{k}}_{\sigma _r}(B)={2^{{\overline{J}}_{\sigma _{r}}+l'}}\\ \displaystyle {\overline{k}}_{\sigma _r}\left( \frac{B}{2}\right) ={2^{{\overline{J}}_{\sigma _{r}}+l'+1}}\\ \end{array} \right. \Rightarrow {\overline{k}}_{\sigma _r}(B)=\frac{1}{2}{\overline{k}}_{\sigma _r}\left( \frac{B}{2}\right) . \end{aligned}$$

• (ii) Suppose $B\in [w_{{\bar{l}}+(l'-1)n+i+1},w_{{\bar{l}}+(l'-1)n+i})$ for some $l\in \{1,2,\ldots \}$ and $i= n$. Then $\displaystyle B\in \left[ \frac{{\widetilde{B}}_{1}}{2^{l'+1}},\frac{{\widetilde{B}}_{n}}{2^{l'}}\right)$ and $\displaystyle 2^{l'} B\in \left[ \frac{{\widetilde{B}}_{1}}{2},{\widetilde{B}}_{n}\right)$.

  • Given $r\in \{1,2,\ldots ,n\}$. Then $\displaystyle 2^lB\in \left[ \frac{{\widetilde{B}}_{r}}{2},{\widetilde{B}}_{r}\right)$ holds, since

    $$\begin{aligned} \frac{{\widetilde{B}}_{r}}{2}\le \cdots \le \frac{{\widetilde{B}}_{1}}{2}\le {\widetilde{B}}_{n}\le \cdots \le {\widetilde{B}}_{r}. \end{aligned}$$

    Moreover,

    $$\begin{aligned}&\displaystyle 2^{l'}B\in \left( \frac{{\widetilde{B}}_{r}}{2},{\widetilde{B}}_{r}\right) \Rightarrow B\in \left( \frac{{\widetilde{B}}_{r}}{2^{l'+1}},\frac{{\widetilde{B}}_{r}}{2^{l'}}\right) \Rightarrow \left\{ \begin{array}{ll} B\in \left[ B_{\sigma _{r}}^{2^{{\overline{J}}_{\sigma _{r}}+l'+1}},B_{\sigma _{r}}^{2^{{\overline{J}}_{\sigma _{r}}+l'}}\right) \\ \displaystyle \frac{B}{2}\in \left[ B_{\sigma _{r}}^{2^{{\overline{J}}_{\sigma _{r}}+l'+2}},B_{\sigma _{r}}^{2^{{\overline{J}}_{\sigma _{r}}+l'+1}}\right) \\ \end{array} \right. \\&\quad \Rightarrow \left\{ \begin{array}{ll} \displaystyle {\overline{k}}_{\sigma _r}(B)={2^{{\overline{J}}_{\sigma _{r}}+l'+1}}\\ \displaystyle {\overline{k}}_{\sigma _r}\left( \frac{B}{2}\right) ={2^{{\overline{J}}_{\sigma _{r}}+l'+2}}\\ \end{array} \right. \Rightarrow {\overline{k}}_{\sigma _r}(B)=\frac{1}{2}{\overline{k}}_{\sigma _r}\left( \frac{B}{2}\right) . \end{aligned}$$

Therefore, (18) holds for $\displaystyle {\bar{l}}=n-1+\sum _{i=1}^{n}{\overline{J}}_i$. $\square$

1.7 Proof of Theorem 5

Proof

By Proposition 4, for all $l\ge {\bar{l}}$,

$$\begin{aligned} w_{l}=2w_{l+n} \end{aligned}$$

and

$$\begin{aligned} {\overline{k}}_i(B)=\frac{1}{2}{\overline{k}}_i(B/2), \forall i\in \Lambda , B\in (0,w_{{\overline{l}}+1}). \end{aligned}$$

Assume $B\in (0,w_{{\overline{l}}+1})$. Then $\displaystyle B{\overline{k}}_i(B)=\left( \frac{B}{2}\right) \left( 2{\overline{k}}_i\left( B\right) \right) =\left( \frac{B}{2}\right) \left( {\overline{k}}_i\left( \frac{B}{2}\right) \right)$ for all $i\in \Lambda$. Hence

$$\begin{aligned} {\phi }_i(B{\overline{k}}_i(B))={\phi }_i\left( {\overline{k}}_i\left( \frac{B}{2}\right) \left( \frac{B}{2}\right) \right) \end{aligned}$$

for all $i\in \Lambda$. Therefore,

$$\begin{aligned} \frac{A_0}{B/2}+\sum _{i=1}^{n}{\phi }_i\left( {\overline{k}}_i\left( \frac{B}{2}\right) \left( \frac{B}{2}\right) \right) \gvertneqq \frac{A_0}{B}+\sum _{i=1}^{n}{\phi }_i(B{\overline{k}}_i(B)), \forall B<w_{{\overline{l}}} \end{aligned}$$

implies that the optimal solution $B^*$ must be greater than $w_{{\overline{l}}+n}$. Similarly, this result can be extended such that the optimal solution $B^*$ must be greater than $w_{{\overline{l}}+1}$. $\square$

1.8 Proof of Proposition 6

Proof

• (1) If $w_{l-1}\le \displaystyle \frac{M_{\rho _{n}}}{{\overline{k}}_{\rho _{n}}^{l}}$, then there are no break points in the interval $[w_{l},w_{l-1}]$ and for all $i\in \Lambda$

  $$\begin{aligned} B\le w_{l-1} \Rightarrow B< \frac{M_{\rho _{i}}}{{{\overline{k}}_{\rho _{i}}^{l}}} \Rightarrow {\overline{k}}_{\rho _{i}}^{l} B < M_{\rho _{i}}. \end{aligned}$$

  (35)

  The explicit form of the objective function $\displaystyle \frac{A_0}{B}+\sum _{i=1}^{n}{\phi }_i({\overline{k}}_i(B) B)$ is

  $$\begin{aligned} \begin{array}{rcl} \displaystyle \frac{A_0}{B}+\sum _{i=1}^{n}{\phi }_i({\overline{k}}_i(B) B)&{}=&{}\displaystyle \frac{A_0}{B}+\sum _{i=1}^{n}{\phi }_{\rho _{i}}({\overline{k}}_{\rho _i}(B) B)\\ &{}=&{}\displaystyle \frac{A_0}{B}+\sum _{i=1}^{n}{\phi }_{\rho _{i}}({\overline{k}}_{\rho _{i}}^{l} B)\\ &{}=&{}\displaystyle \sum _{i=1}^{n}{\phi }_{\rho _{i}}^1({\overline{k}}_{\rho _{i}}^{l} B)\quad (\because (35))\\ &{}=&{}\displaystyle E_{n}^lB+F_{n}^l+\frac{G_{n}^l}{B}.\\ \end{array} \end{aligned}$$

• (2) If $\displaystyle \frac{M_{\rho _{1}}}{{{\overline{k}}_{\rho _{1}}^{l}}}<w_{l}$, then there are also no break points in the interval $[w_{l},w_{l-1}]$ and for all $i\in \Lambda$

  $$\begin{aligned} w_{l}\le B\Rightarrow \frac{M_{\rho _{i}}}{{{\overline{k}}_{\rho _{i}}^{l}}}< B \Rightarrow M_{\rho _{i}}<{\overline{k}}_{\rho _{i}}^{l}B \end{aligned}$$

  (36)

  The explicit form of the objective function $\displaystyle \frac{A_0}{B}+\sum _{i=1}^{n}{\phi }_i({\overline{k}}_i(B) B)$ is

  $$\begin{aligned} \begin{array}{rcl} \displaystyle \frac{A_0}{B}+\sum _{i=1}^{n}{\phi }_i({\overline{k}}_i(B) B)&{}=&{}\displaystyle \frac{A_0}{B}+\sum _{i=1}^{n}{\phi }_{\rho _{i}}({\overline{k}}_{\rho _{i}}^{l} B)\\ &{}=&{}\displaystyle \frac{A_0}{B}+\sum _{i=1}^{n}{\phi }_{\rho _{i}}^2({\overline{k}}_{\rho _{i}}^{l} B)\quad (\because (36))\\ &{}=&{}\displaystyle E_{0}^lB+F_{0}^l+\frac{G_{0}^l}{B}.\\ \end{array} \end{aligned}$$

• (3) If $w_{l-1}\ge \displaystyle \frac{M_{\rho _{n}}}{{{\overline{k}}_{\rho _{n}}^{l}}}$, we define $\displaystyle {\underline{j}}$ as the smallest index $i\in \Lambda$ such that $\displaystyle \frac{M_{\rho _{i}}}{{{\overline{k}}_{\rho _{i}}^l}}\le w_{l-1}$, i.e.,

  $$\begin{aligned} \displaystyle {\underline{j}} = \min _{i\in \Lambda }\left\{ i\left| \displaystyle \frac{M_{\rho _{i}}}{{{\overline{k}}_{\rho _{i}}^{l}}}\le w_{l-1}\right. \right\} . \end{aligned}$$

  If $\displaystyle \frac{M_{\rho _{1}}}{{\overline{k_{\rho _{1}}^{l}}}}\ge w_{l}$, we define $\displaystyle {\overline{j}}$ as the largest index $i\in \Lambda$ such that $\displaystyle w_{l}\le \frac{M_{\rho _{i}}}{{{\overline{k}}_{\rho _{i}}^{l}}}$, i.e.,

  $$\begin{aligned} \displaystyle {\overline{j}} = \max _{i\in \Lambda }\left\{ i\left| \displaystyle w_{l}\le \frac{M_{\rho _{i}}}{{{\overline{k}}_{\rho _{i}}^{l}}}\right. \right\} . \end{aligned}$$

  Hence if $w_{l-1}\ge \displaystyle \frac{M_{\rho _{n}}}{{{\overline{k}}_{\rho _{n}}^{l}}}$ and $\displaystyle \frac{M_{\rho _{1}}}{{{\overline{k}}_{\rho _{1}}^{l}}}\ge w_{l}$, then there are

  $$\begin{aligned} {\overline{j}}-{\underline{j}}+1 \end{aligned}$$

  break points in the interval $[w_{l},w_{l-1}]$. Hence we consider the following ${\overline{j}}-{\underline{j}}+2$ subintervals

  $$\begin{aligned} \displaystyle \left( \frac{M_{\rho _{{\underline{j}}}}}{{\overline{k}}_{\rho _{{\underline{j}}}}^{l}}, w_{l-1}\right) , \left\{ \displaystyle \left( \frac{M_{\rho _{{\underline{j}}+j-1}}}{{\overline{k}}_{\rho _{{\underline{j}}+j-1}}^{l}} , \frac{M_{\rho _{{\underline{j}}+j-2}}}{{\overline{k}}_{\rho _{{\underline{j}}+j-2}}^{l}} \right) \right\} _{j\in \{2,3,\ldots ,{\overline{j}}-{\underline{j}}+1\}}, \displaystyle \left( w_{l}, \frac{M_{\rho _{{\overline{j}}}}}{{\overline{k}}_{\rho _{{\overline{j}}}}^{l}}\right) \end{aligned}$$

  (37)

  of $[w_{l},w_{l-1}]$. Similar to the cases: $w_{l-1}<\displaystyle \frac{M_{\rho _{n}}}{{{\overline{k}}_{\rho _{n}}^{l}}}$ and $\displaystyle \frac{M_{\rho _{1}}}{{{\overline{k}}_{\rho _{1}}^{l}}}<w_{l}$, in every subinterval of (37), we describe the explicit form of the objective function $\displaystyle \frac{A_0}{B}+\sum _{i=1}^{n}{\phi }_i({\overline{k}}_i(B) B)$ as follows.

  • Suppose $B\in \displaystyle \left( \frac{M_{\rho _{{\underline{j}}}}}{{\overline{k}}_{\rho _{{\underline{j}}}}}, w_{l-1}\right)$. Hence, if $i\le {\underline{j}}-1$, then ${\phi }_{\rho _{i}}({\overline{k}}_{\rho _{i}}^{l} B)={\phi }_{\rho _{i}}^1({\overline{k}}_{\rho _{i}}^{l} B)$. Otherwise, ${\phi }_{\rho _{i}}({\overline{k}}_{\rho _{i}}^{l} B)={\phi }_{\rho _{i}}^2({\overline{k}}_{\rho _{i}}^{l} B)$. Therefore,

  $$\begin{aligned} \begin{array}{rcl} \displaystyle \frac{A_0}{B}+\sum _{i=1}^{n}{\phi }_i({\overline{k}}_i(B) B) &{}=&{}\displaystyle \frac{A_0}{B}+\sum _{i=1}^{{\underline{j}}-1}{\phi }_{\rho _{i}}^{1}({\overline{k}}_{\rho _{i}}^{l} B) +\sum _{i={\underline{j}}}^{n} {\phi }_{\rho _{i}}^{2}({\overline{k}}_{\rho _{i}}^{l} B)\\ &{}=&{}\displaystyle E_{{\underline{j}}-1}^{l}B+F_{{\underline{j}}-1}^{l}+\frac{G_{{\underline{j}}-1}^{l}}{B}.\\ \end{array} \end{aligned}$$

  • Suppose $j\in \{2,3,\ldots ,{\overline{j}}-{\underline{j}}+1\}$ and $B\in \displaystyle \left( \frac{M_{\rho _{{\underline{j}}+j-1}}}{{\overline{k}}_{\rho _{{\underline{j}}+j-1}}} , \frac{M_{\rho _{{\underline{j}}+j-2}}}{{\overline{k}}_{\rho _{{\underline{j}}+j-2}}} \right)$. Hence, if $i\le {\underline{j}}+j-2$, then ${\phi }_{\rho _{i}}({\overline{k}}_{\rho _{i}}^{l} B)={\phi }_{\rho _{i}}^1({\overline{k}}_{\rho _{i}}^{l} B)$. Otherwise, ${\phi }_{\rho _{i}}({\overline{k}}_{\rho _{i}}^{l} B)={\phi }_{\rho _{i}}^2({\overline{k}}_{\rho _{i}}^{l}B)$. Therefore,

  $$\begin{aligned} \begin{array}{rcl} \displaystyle \frac{A_0}{B}+\sum _{i=1}^{n}{\phi }_i({\overline{k}}_i(B) B)&{}=&{}\displaystyle \frac{A_0}{B}+\sum _{i=1}^{{\underline{j}}+j-2}{\phi }_{\rho _{i}}^{1}({\overline{k}}_{\rho _{i}}^{l} B) +\sum _{i={\underline{j}}+j-1}^{n} {\phi }_{\rho _{i}}^{2}({\overline{k}}_{\rho _{i}}^{l} B)\\ &{}=&{}\displaystyle E_{{\underline{j}}+j-2}^{l}B+F_{{\underline{j}}+j-2}^{l}+\frac{G_{{\underline{j}}+j-2}^{l}}{B}.\\ \end{array} \end{aligned}$$

  • Suppose $B\in \displaystyle \left( w_{l}, \frac{M_{\rho ({\overline{j}})}}{{\overline{k}}_{\rho ({\overline{j}})}}\right)$. Hence, if $i\le {\overline{j}}$, then ${\phi }_{\rho _{i}}({\overline{k}}_{\rho _{i}}^{l} B)={\phi }_{\rho _{i}}^1({\overline{k}}_{\rho _{i}}^{l} B)$. Otherwise, ${\phi }_{\rho _{i}}(\overline{k_{\rho _{i}}^{l} }B)={\phi }_{\rho _{i}}^2({\overline{k}}_{\rho _{i}}^{l} B)$. Therefore,

  $$\begin{aligned} \begin{array}{rcl} \displaystyle \frac{A_0}{B}+\sum _{i=1}^{n}{\phi }_i({\overline{k}}_i(B) B)&{}=&{}\displaystyle \frac{A_0}{B}+\sum _{i=1}^{{\overline{j}}}{\phi }_{\rho _{i}}^{1}({\overline{k}}_{\rho _{i}}^{l} B) +\sum _{i={\overline{j}}+1}^{n} {\phi }_{\rho _{i}}^{2}({\overline{k}}_{\rho _{i}}^{l} B)\\ &{}=&{}\displaystyle E_{{\overline{j}}}^{l}B+F_{{\overline{j}}}^{l}+\frac{G_{{\overline{j}}}^{l}}{B}.\\ \end{array} \end{aligned}$$

$\square$

1.9 Proof of Theorem 7

Proof

• (1) By Proposition 6,

  $$\begin{aligned}&w_{l-1}<\displaystyle \frac{M_{\rho {(n)}}}{{k_{\rho {(n)}}}} \Rightarrow \frac{A_0}{B}+\sum _{i=1}^{n}{\phi }_i({\overline{k}}_i(B) B)=E_n^{l}B+F_n^{l}+\frac{G_n^{l}}{B}\\&\quad \Rightarrow \frac{d}{dB}\left( \frac{A_0}{B}+\sum _{i=1}^{n}{\phi }_i({\overline{k}}_i(B) B) \right) =E_n^{l}-\frac{G_n^{l}}{B^2}. \end{aligned}$$

  Hence the stationary point of $\displaystyle \frac{A_0}{B}+\sum _{i=1}^{n}{\phi }_i({\overline{k}}_i(B) B)$ is $\displaystyle \sqrt{\frac{G_n^{l}}{E_n^{l}}}$.

• (1a) Since $\displaystyle \sqrt{\frac{G_n^{l}}{E_n^{l}}} <w_{l}$ and the objective function $\displaystyle \frac{A_0}{B}+\sum _{i=1}^{n}{\phi }_i({\overline{k}}_i(B) B)$ is strictly convex, the optimal solution of (24) is $w_{l}$.

• (1b) Since $\displaystyle \sqrt{\frac{G_n^{l}}{E_n^{l}}}\in [w_{l}, w_{l-1}]$ and the objective function $\displaystyle \frac{A_0}{B}+\sum _{i=1}^{n}{\phi }_i({\overline{k}}_i(B) B)$ is strictly convex, the optimal solution of (24) is $\sqrt{\frac{G_{n}^{l}}{E_{n}^{l}}}$.

• (1c) Since $\sqrt{\frac{G_{n}^{l}}{E_{n}^{l}}}> w_{l-1}$ and the objective function $\displaystyle \frac{A_0}{B}+\sum _{i=1}^{n}{\phi }_i({\overline{k}}_i(B) B)$ is strictly convex, the optimal solution of (24) is $w_{l-1}$.

• (2) By Proposition 6,

  $$\begin{aligned}&\displaystyle \frac{M_{\rho {(1)}}}{{k_{\rho {(1)}}}}<w_{l} \Rightarrow \frac{A_0}{B}+\sum _{i=1}^{n}{\phi }_i({\overline{k}}_i(B) B)=E_0^{l}B+F_0^{l}+\frac{G_0^{l}}{B}\\&\quad \Rightarrow \frac{d}{dB}\left( \frac{A_0}{B}+\sum _{i=1}^{n}{\phi }_i({\overline{k}}_i(B) B) \right) =E_0^{l}-\frac{G_0^{l}}{B^2}. \end{aligned}$$

  Hence the stationary point of $\displaystyle \frac{A_0}{B}+\sum _{i=1}^{n}{\phi }_i({\overline{k}}_i(B) B)$ is $\displaystyle \sqrt{\frac{G_0^{l}}{E_0^{l}}}$.

• (2a) Since $\displaystyle \sqrt{\frac{G_0^{l}}{E_0^{l}}} <w_{l}$ and the objective function $\displaystyle \frac{A_0}{B}+\sum _{i=1}^{n}{\phi }_i({\overline{k}}_i(B) B)$ is strictly convex, the optimal solution of (24) is $w_{l}$.

• (2b) Since $\displaystyle \sqrt{\frac{G_0^{l}}{E_0^{l}}}\in [w_{l}, w_{l-1}]$ and the objective function $\displaystyle \frac{A_0}{B}+\sum _{i=1}^{n}{\phi }_i({\overline{k}}_i(B) B)$ is strictly convex, the optimal solution of (24) is $\displaystyle \sqrt{\frac{G_{0}^{l}}{E_{0}^{l}}}$.

• (2c) Since $\displaystyle \sqrt{\frac{G_{0}}{E_{0}}}> w_{l-1}$ and the objective function $\displaystyle \frac{A_0}{B}+\sum _{i=1}^{n}{\phi }_i({\overline{k}}_i(B) B)$ is strictly convex, the optimal solution of (24) is $w_{l-1}$.

• (3a) The objective function $\displaystyle \frac{A_0}{B}+\sum _{i=1}^{n}{\phi }_i({\overline{k}}_i(B) B)$ is strictly convex, hence the derivative of the objective function at $w_{l-1}$ is negative implies the optimal solution of (24) is $w_{l-1}$.

• (3b) The objective function $\displaystyle \frac{A_0}{B}+\sum _{i=1}^{n}{\phi }_i({\overline{k}}_i(B) B)$ is strictly convex, hence the derivative of the objective function at $w_{l}$ is positive implies the optimal solution of (24) is $w_{l}$.

• (3c) If the derivative of the objective function at $w_{l}$ is negative and the derivative of the objective function at $w_{l-1}$ is positive, then there exists exactly one of the following subintervals

  $$\begin{aligned} \displaystyle \left[ \frac{M_{\rho _{{\underline{j}}}}}{{\overline{k}}_{\rho _{{\underline{j}}}}^{l}}, w_{l-1}\right] , \left\{ \displaystyle \left[ \frac{M_{\rho _{{\underline{j}}+j-1}}}{{\overline{k}}_{\rho _{{\underline{j}}+j-1}}^{l}} , \frac{M_{\rho _{{\underline{j}}+j-2}}}{{\overline{k}}_{\rho _{{\underline{j}}+j-2}}^{l}} \right] \right\} _{j\in \{2,3,\ldots ,{\overline{j}}-{\underline{j}}+1\}}, \displaystyle \left[ w_{l}, \frac{M_{\rho _{{\overline{j}}}}}{{\overline{k}}_{\rho _{{\overline{j}}}}^{l}}\right] \end{aligned}$$

  such that the derivative has opposite sign at the endpoints of this subinterval. Hence the optimal solution of (24) must occur on the interval between these two consecutive points of the sequence (26). Then by Proposition 6, the coefficients of $\displaystyle \frac{A_0}{B}+\sum _{i=1}^{n}{\phi }_i({\overline{k}}_i(B) B)$ on this subinterval can be determined, so the optimal solution of (24) also can be determined.

$\square$