Skip to main content
SpringerLink
Log in

hp-Version a priori Error Analysis of Interior Penalty Discontinuous Galerkin Finite Element Approximations to the Biharmonic Equation

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

Abstract

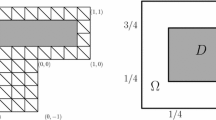
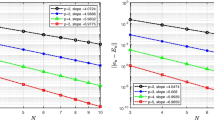
We consider the symmetric formulation of the interior penalty discontinuous Galerkin finite element method for the numerical solution of the biharmonic equation with Dirichlet boundary conditions in a bounded polyhedral domain in \(\mathbb{R}^d, d \geqslant 2\). For a shape-regular family of meshes consisting of parallelepipeds, we derive hp-version a priori bounds on the global error measured in the L2 norm and in broken Sobolev norms. Using these, we obtain hp-version bounds on the error in linear functionals of the solution. The bounds are optimal with respect to the mesh size h and suboptimal with respect to the degree of the piecewise polynomial approximation p. The theoretical results are confirmed by numerical experiments, and some practical applications in Poisson–Kirchhoff thin plate theory are presented.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Arnold D.N., Brezzi F., Cockburn B., Marini D. (2001). Unified analysis of discontinuous Galerkin methods for elliptic problems. SIAM J. Numer. Anal. 39(5): 1749–1779

    Article  MathSciNet  Google Scholar 

  2. Babuška I., Miller A. (1984). The post-processing approach in the finite element method—part 1: Calculation of displacements, stresses and other higher derivatives of the displacements. Int. J. Numer. Meth. Eng. 20(6): 1085–1109

    Article  Google Scholar 

  3. Babuška I., Miller A. (1984). The post-processing approach in the finite element method—part 2: The calculation of stress intensity factors. Int. J. Numer. Meth. Eng. 20(6): 1111–1129

    Article  Google Scholar 

  4. Babuška I., Miller A. (1984). The post-processing approach in the finite element method—part 3: A posteriori error estimates and adaptive mesh selection. Int. J. Num. Meth. Eng. 20(6): 2311–2325

    Article  Google Scholar 

  5. Babuška I., Suri M. (1987). The hp-version of the finite element method with quasiuniform meshes. Math. Model. Numer. Anal. 21: 199–238

    Google Scholar 

  6. Baker G. (1977). Finite element methods for elliptic equations using nonconforming . Math. Comp. 31: 44–59

    Google Scholar 

  7. Blum H., Rannacher R. (1980). On the boundary value problem of the biharmonic operator on domains with angular corners. Math. Meth. Appl. Sci. 2: 556–581

    MATH  MathSciNet  Google Scholar 

  8. Brenner S.C., Scott L.R.(2002). The Mathematical Theory of Finite Element Methods, 2nd edn. Spinger, Berlin

    MATH  Google Scholar 

  9. Brezzi F., Fortin M. (1991). Mixed and Hybrid Finite Element Methods. Springer, Berlin

    MATH  Google Scholar 

  10. Ciarlet P.G. (1991). Basic error estimates for elliptic problems. In: Ciarlet P., Lions J. (eds), Handbook of Numerical Analysis, Vol.2. North Holland, Amsterdam

    Google Scholar 

  11. Cockburn B., Karniadakis G.E., Shu C.-W. (eds) (2000). Discontinuous Galerkin Methods, LNCSE, Vol.11, Springer, Berlin

    Google Scholar 

  12. Douglas J.J., Dupont T. (1976). Interior penalty procedures for elliptic and parabolic Galerkin methods. Lectures Notes in Physics Vol.58. Springer-Verlag, Berlin

    Google Scholar 

  13. Engel G., Garikipati K., Hughes T., Larson M., Mazzei L., Taylor R. (2002). Continuous/discontinuous finite element approximations of fourth-order elliptic problems in structural and continuum mechanics with applications to thin beams and plates, and strain gradient elasticity. Comput. Meth. Appl. Mech. Eng. 191: 3669–3750

    Article  MATH  MathSciNet  Google Scholar 

  14. Georgoulis E.H., Süli E. (2005). Optimal error estimates for the hp-version interior penalty discontinuous Galerkin finite element method. IMA J. Numer. Anal. 25: 205–220

    Article  MATH  MathSciNet  Google Scholar 

  15. Girault V., Raviart P. (1986). Finite Element Methods for Navier-Stokes Equations, Theory and Algorithms. Spring-Verlag, Berlin

    MATH  Google Scholar 

  16. Grisvard P. (1992). Singularities in Boundary Value Problems. Research Notes in Applied Mathematics. Masson, Paris

    MATH  Google Scholar 

  17. Harriman K., Gavaghan D.J., and Süli E. (2004) The Importance of Adjoint Consistency in the Approximations of Linear Functionals Using the Discontinuous Galerkin Finite Element Method. Tech. Rep. 04/18, Oxford University Computing Laboratory.

  18. Harriman K., Houston P., Senior B., Süli E. (2002). hp-version Galerkin methods with interior penalty for partial differential equations with characteristic form. In: Shu C.-W., Tang T., Cheng S.-Y. (eds), Recent Advances in Scientific Computing and Partial Differential Equations, Contemporary Mathematics Vol. 330, AMS, 2003 pp. 89-119

  19. Kanschat G., Rannacher R. (2002). Local error analysis of the interior penalty discontinuous Galerkin method for second order elliptic problems. J. Numer. Math. 10(4): 249–274

    MATH  MathSciNet  Google Scholar 

  20. Kozlov V.A., Maz’ya, V.G. (1996). Singularities in solutions to mathematical physics problems in non-smooth domains. In: Cea J. et al. (ed), Partial Differential Equations and Functional Analysis. Proceedings of the conference held in November 1994 in memory of Pierre Grisvard. Progr. Nonlinear Differential Equations Appl., Vol. 22, Birkhäuser Boston, Boston MA. pp. 174–206

    Google Scholar 

  21. Larson M., Niklasson A. (2004). Analysis of a family of discontinuous Galerkin methods for elliptic problems: the one dimensional case. Numer. Math. 99(1): 113–130

    Article  MATH  MathSciNet  Google Scholar 

  22. Mozolevski I., Süli E. (2003). A priori error analysis for the hp-version of the discontinuous Galerkin finite element method for the biharmonic equation. Comput. Meth. Appl. Math. 3(4): 596–607

    MATH  Google Scholar 

  23. Oden J.T., Babuška I., Baumann C. (1998). The local discontinuous Galerkin finite element method for diffusion problems. J. Comput. Phys. 146: 491–519

    Article  MATH  MathSciNet  Google Scholar 

  24. Rivière B., Wheeler M.F., Girault V. (2001). A priori error estimates for finite element methods based on discontinuous approximation spaces for elliptic problems. J.Numer. Anal. 39(3): 902–931

    Article  MATH  MathSciNet  Google Scholar 

  25. Schwab C. (1998). p- and hp- Finite Element Methods. Theory and Applications to Solid and Fluid Mechanics. Oxford University Press, Oxford

    Google Scholar 

  26. Süli E., Mozolevski I. (2004). hp-version Interior Penalty DGFEMs for the Biharmonic Equation. Techinical Report 04/05, Oxford University Computing Laboratory. http://web.comlab.ox.ac.uk/oucl/publications/natr/na-04-05.html

  27. Timoshenko S.P., Woinowsky-Krieger S. (1984). Theory of plates and shells, 25edn. McGraw-Hill International Book Company, New york

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Mathematics Department, Federal University of Santa Catarina, Trindade, Florianópolis, SC- 88040-900, Brazil

    Igor Mozolevski

  2. Computing Laboratory, University of Oxford, Wolfson Building, Parks Road, Oxford, OX1 3QD, UK

    Endre Süli

  3. Applied Mathematics Department, IME, University of São Paulo, Rua do Matão 1010, São Paulo, SP- 05508-090, Brazil

    Paulo R. Bösing

Authors
  1. Igor Mozolevski
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Endre Süli
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Paulo R. Bösing
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Igor Mozolevski.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Mozolevski, I., Süli, E. & Bösing, P.R. hp-Version a priori Error Analysis of Interior Penalty Discontinuous Galerkin Finite Element Approximations to the Biharmonic Equation. J Sci Comput 30, 465–491 (2007). https://doi.org/10.1007/s10915-006-9100-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10915-006-9100-1

Keywords

Search

Navigation