Skip to main content
SpringerLink
Log in

An Analysis of the Dissipation and Dispersion Errors of the P N P M Schemes

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

Abstract

We examine the dispersion and dissipation properties of the P N P M schemes for linear wave propagation problems. P N P M scheme are based on P N discontinuous Galerkin base approximations augmented with a cell centered polynomial least-squares reconstruction from degree N up to the design polynomial degree M. This methodology can be seen as a generalized discretization framework, as cell centered high order finite volume schemes (N=0) and discontinuous Galerkin schemes (N=M) are included as special cases.

We show that with respect to the dispersion error, the pure discontinuous Galerkin variant gives typically the best accuracy for a defined number of points per wavelength. Regarding the dissipation behavior, combinations of N and M exist that result in slightly lower errors for a given resolution. An investigation of the influence of the stencil size on the accuracy of the scheme shows that the errors are smaller the smaller the stencil size for the reconstruction.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

References

  1. Ainsworth, M.: Dispersive and dissipative behaviour of high order discontinuous Galerkin finite element methods. J. Comput. Phys. 198(1), 106–130 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  2. Bassi, F., Rebay, S.: A high-order accurate discontinuous finite element method for the numerical solution of the compressible Navier-Stokes equations. J. Comput. Phys. 131, 267–279 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  3. Dumbser, M.: Arbitrary High Order Schemes for the Solution of Hyperbolic Conservation Laws in Complex Domains. Shaker Verlag, Aachen (2005)

    Google Scholar 

  4. Dumbser, M., Balsara, D.S., Toro, E.F., Munz, C.-D.: A unified framework for the construction of one-step finite-volume and discontinuous Galerkin schemes on unstructured meshes. J. Comput. Phys. 227, 8209–8253 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  5. Dumbser, M., Käser, M., Titarev, V.A., Toro, E.F.: Quadrature-free non-oscillatory finite volume schemes on unstructured meshes for nonlinear hyperbolic systems. J. Comput. Phys. 226, 204–243 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  6. Dumbser, M., Munz, C.-D.: Arbitrary high order discontinuous Galerkin schemes. In: Cordier, S., Goudon, T., Gutnic, M., Sonnendrucker, E. (eds.) Numerical Methods for Hyperbolic and Kinetic Problems. IRMA Series in Mathematics and Theoretical Physics, pp. 295–333. EMS Publishing House, Zurich (2005)

    Chapter  Google Scholar 

  7. Dumbser, M.: Arbitrary high order pnpm schemes on unstructured meshes for the compressible Navier-Stokes equations. Comput. Fluids 39(1), 60–76 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  8. Hu, F.Q., Hussaini, M.Y., Rasetarinera, P.: An analysis of the discontinuous Galerkin method for wave propagation problems. J. Comput. Phys. 151(2), 921–946 (1999)

    Article  MATH  Google Scholar 

  9. Lo, M., van Leer, B.: Analysis and implementation of recovery-based discontinuous Galerkin for diffusion. In: 19th AIAA Computational Fluid Dynamics Conference (AIAA-2009-3786), June (2009)

    Google Scholar 

  10. Luo, H., Luo, L., Nourgaliev, R., Mousseau, V.A., Dinh, N.: A reconstructed discontinuous Galerkin method for the compressible Navier-Stokes equations on arbitrary grids. J. Comput. Phys. 229(19), 6961–6978 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  11. Park, H., Nourgaliev, R., Mousseau, V., Knoll, D.: Recovery discontinuous Galerkin Jacobian-free Newton Krylov method for all-speed flows. Tech. rep. inl/con-08- 13822, Idaho National Laboratory (2008)

  12. Toro, E.F.: Riemann Solvers and Numerical Methods for Fluid Dynamics. Springer, Berlin (1999)

    MATH  Google Scholar 

  13. van Leer, B., Lo, M.: Unification of discontinuous Galerkin methods for advection and diffusion. In: 19th AIAA Computational Fluid Dynamics Conference (AIAA-2009-0400), June (2009)

    Google Scholar 

  14. van Leer, B., Lo, M., van Raalte, M.: Discontinuous Galerkin method for diffusion based on recovery. In: 18th AIAA Computational Fluid Dynamics Conference (AIAA-2007-4083), June (2007)

    Google Scholar 

  15. van Leer, B., Nomura, S.: Discontinuous Galerkin for diffusion. In: 17th AIAA Computational Fluid Dynamics Conference (AIAA-2005-5108), 6–9 June (2005)

    Google Scholar 

  16. van Raalte, M., van Leer, B.: Bilinear forms for the recovery-based discontinuous Galerkin method for the diffusion. Commun. Comput. Phys. 5, 683–693 (2009)

    MathSciNet  Google Scholar 

Download references

Acknowledgements

The author thanks the reviewers for their valuable comments. This project is kindly supported by the Deutsche Forschungsgemeinschaft (DFG) within SPP 1276: MetStroem and the research project IDIHOM within the European Research Framework Programme.

Author information

Authors and Affiliations

  1. Institute for Aerodynamics and Gasdynamics, University of Stuttgart, Pfaffenwaldring 21, 70550, Stuttgart, Germany

    Gregor J. Gassner

Authors
  1. Gregor J. Gassner
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Gregor J. Gassner.

Appendices

Appendix A: Dispersion Relation for the P N P M Schemes

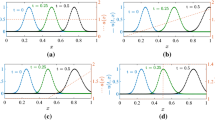
In this section, the dispersion relation plots for all combinations of N and M up to 4 are shown. Furthermore, the accuracy results of all combinations for given points per wavelength and the resulting convergence error behavior are listed in Tables 12–19 (Figs. 5, 6, 7, 8, 9).

Fig. 5
figure 5

Plot of the dispersion relation for M=1 for different polynomial degrees N with N≤M. Quantities with superscript ∗ are normalized with the corresponding value N+1

Full size image
Fig. 6
figure 6

Plot of the dispersion relation for M=2 for different polynomial degrees N with N≤M. Quantities with superscript ∗ are normalized with the corresponding value N+1

Full size image
Fig. 7
figure 7

Plot of the dispersion relation for M=3 for different polynomial degrees N with N≤M. Quantities with superscript ∗ are normalized with the corresponding value N+1

Full size image
Fig. 8
figure 8

Plot of the dispersion relation for M=4 for different polynomial degrees N with N≤M. Quantities with superscript ∗ are normalized with the corresponding value N+1

Full size image
Fig. 9
figure 9

Plot of the dissipation relation for M=1 for different polynomial degrees N with N≤M. Quantities with superscript ∗ are normalized with the corresponding value N+1

Full size image
Table 12 Dispersion error \(\delta:=|{\operatorname{Re}}(\varOmega (K)) - K|\) for the P N P M schemes with M=1 and different N≤M. The most accurate result in each row is marked in bold
Full size table
Table 13 Order of convergence of the dispersion error for the P N P M schemes with M=1 and different N≤M
Full size table
Table 14 Dispersion error \(\delta:=|{\operatorname{Re}}(\varOmega (K)) - K|\) for the P N P M schemes with M=2 and different N≤M. The most accurate result in each row is marked in bold
Full size table
Table 15 Order of convergence of the dispersion error for the P N P M schemes with M=2 and different N≤M
Full size table
Table 16 Dispersion error \(\delta:=|{\operatorname{Re}}(\varOmega (K)) - K|\) for the P N P M schemes with M=3 and different N≤M. The most accurate result in each row is marked in bold
Full size table
Table 17 Order of convergence of the dispersion error for the P N P M schemes with M=3 and different N≤M
Full size table
Table 18 Dispersion error \(\delta:=|{\operatorname{Re}}(\varOmega (K)) - K|\) for the P N P M schemes with M=4 and different N≤M. The most accurate result in each row is marked in bold
Full size table
Table 19 Order of convergence of the dispersion error for the P N P M schemes with M=4 and different N≤M
Full size table

Appendix B: Dissipation Relation for the P N P M Schemes

In this section, the dissipation relation plots for all combinations of N and M up to 4 are shown. Furthermore, the accuracy results of all combinations for given points per wavelength and the resulting convergence error behavior are listed in Tables 20–27 (Figs. 10, 11, 12).

Fig. 10
figure 10

Plot of the dissipation relation for M=2 for different polynomial degrees N with N≤M. Quantities with superscript ∗ are normalized with the corresponding value N+1

Full size image
Fig. 11
figure 11

Plot of the dissipation relation for M=3 for different polynomial degrees N with N≤M. Quantities with superscript ∗ are normalized with the corresponding value N+1

Full size image
Fig. 12
figure 12

Plot of the dissipation relation for M=4 for different polynomial degrees N with N≤M. Quantities with superscript ∗ are normalized with the corresponding value N+1

Full size image
Table 20 Dissipation error \(\delta:=|{\operatorname{Im}}(\varOmega (K))|\) for the P N P M schemes with M=1 and different N≤M. The most accurate result in each row is marked in bold
Full size table
Table 21 Order of convergence of the dissipation error for the P N P M schemes with M=1 and different N≤M
Full size table
Table 22 Dissipation error \(\delta:=|{\operatorname{Im}}(\varOmega (K))|\) for the P N P M schemes with M=2 and different N≤M. The most accurate result in each row is marked in bold
Full size table
Table 23 Order of convergence of the dissipation error for the P N P M schemes with M=2 and different N≤M
Full size table
Table 24 Dissipation error \(\delta:=|{\operatorname{Im}}(\varOmega (K))|\) for the P N P M schemes with M=3 and different N≤M. The most accurate result in each row is marked in bold
Full size table
Table 25 Order of convergence of the dissipation error for the P N P M schemes with M=3 and different N≤M
Full size table
Table 26 Dissipation error \(\delta:=|{\operatorname{Im}}(\varOmega (K))|\) for the P N P M schemes with M=4 and different N≤M. The most accurate result in each row is marked in bold
Full size table
Table 27 Order of convergence of the dissipation error for the P N P M schemes with M=4 and different N≤M
Full size table

Rights and permissions

Reprints and permissions

About this article

Cite this article

Gassner, G.J. An Analysis of the Dissipation and Dispersion Errors of the P N P M Schemes. J Sci Comput 54, 21–44 (2013). https://doi.org/10.1007/s10915-012-9600-0

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10915-012-9600-0

Keywords

Search

Navigation