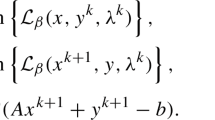Abstract
This short article analyzes an interesting property of the Bregman iterative procedure, which is equivalent to the augmented Lagrangian method, for minimizing a convex piece-wise linear function J(x) subject to linear constraints Ax=b. The procedure obtains its solution by solving a sequence of unconstrained subproblems of minimizing \(J(x)+\frac{1}{2}\|Ax-b^{k}\|_{2}^{2}\), where b k is iteratively updated. In practice, the subproblem at each iteration is solved at a relatively low accuracy. Let w k denote the error introduced by early stopping a subproblem solver at iteration k. We show that if all w k are sufficiently small so that Bregman iteration enters the optimal face, then while on the optimal face, Bregman iteration enjoys an interesting error-forgetting property: the distance between the current point \(\bar{x}^{k}\) and the optimal solution set X ∗ is bounded by ∥w k+1−w k∥, independent of the previous errors w k−1,w k−2,…,w 1. This property partially explains why the Bregman iterative procedure works well for sparse optimization and, in particular, for ℓ 1-minimization. The error-forgetting property is unique to J(x) that is a piece-wise linear function (also known as a polyhedral function), and the results of this article appear to be new to the literature of the augmented Lagrangian method.

Similar content being viewed by others
Notes
The different solvers use different stopping criteria. ISTA and FPC-BB compute the ℓ 2-distance between 0 and the subdifferential of (7), scaled by μ, and compare it with the tolerance. GPSR and SpaRSA use the same ℓ 2-distance except it is not scaled by μ but normalized by the ℓ 2-norm of x instead, along with other minor differences. Underlying Mosek is an interior-point algorithm, which uses stopping criteria based on primal and dual feasibility violations, the duality gap, and the relative complementarity gap. For more details, the interested reader is referred to the companion code of this example.
References
Osher, S., Burger, M., Goldfarb, D., Xu, J., Yin, W.: An iterative regularization method for total variation-based image restoration. Multiscale Model. Simul. 4(2), 460–489 (2005)
Yin, W., Osher, S., Goldfarb, D., Darbon, J.: Bregman iterative algorithms for ℓ 1-minimization with applications to compressed sensing. SIAM J. Imaging Sci. 1(1), 143–168 (2008)
Figueiredo, M., Nowak, R., Wright, S.J.: Gradient projection for sparse reconstruction: application to compressed sensing and other inverse problems. IEEE J. Sel. Top. Signal Process. 4(1), 586–597 (2007). Special Issue on Convex Optimization Methods for Signal Processing
Hale, E.T., Yin, W., Zhang, Y.: Fixed-point continuation for ℓ 1-minimization: methodology and convergence. SIAM J. Optim. 19(3), 1107–1130 (2008)
Wright, S.J., Nowak, R.D., Figueiredo, M.A.T.: Sparse reconstruction by separable approximation. IEEE Trans. Signal Process. 57(7), 2479–2493 (2009)
Xu, J., Osher, S.: Iterative regularization and nonlinear inverse scale space applied to wavelet-based denoising. IEEE Trans. Image Process. 16(2), 534–544 (2006)
Burger, M., Gilboa, G., Osher, S., Xu, J.: Nonlinear inverse scale space methods. Commun. Math. Sci. 4(1), 175–208 (2006)
Burger, M., Osher, S., Xu, J., Gilboa, G.: Nonlinear inverse scale space methods for image restoration. In: Variational, Geometric, and Level Set Methods in Computer Vision. Lecture Notes in Computer Science, vol. 3752, pp. 25–36 (2005)
He, L., Chang, T.-C., Osher, S., Fang, T., Speier, P.: MR image reconstruction by using the iterative refinement method and nonlinear inverse scale space methods. UCLA CAM Report 06-35 (2006)
Ma, S., Goldfarb, D., Chen, L.: Fixed point and Bregman iterative methods for matrix rank minimization. Math. Program. pp 1–33 (2009)
Guo, Z., Wittman, T., Osher, S.: L1 unmixing and its application to hyperspectral image enhancement. In: Proceedings of SPIE Algorithms and Technologies for Multispectral, Hyperspectral, and Ultraspectral Imagery XV, 7334:73341M (2009)
Bregman, L.: The relaxation method of finding the common points of convex sets and its application to the solution of problems in convex programming. U.S.S.R. Comput. Math. Math. Phys. 7, 200–217 (1967)
Cai, J.-F., Osher, S., Shen, Z.: Linearized Bregman iterations for compressed sensing. Math. Comput. 78(267), 1515–1536 (2008)
Cai, J.-F., Osher, S., Shen, Z.: Convergence of the linearized Bregman iteration for ℓ 1-norm minimization. Math. Comput. 78(268), 2127–2136 (2009)
Yin, W.: Analysis and generalizations of the linearized Bregman method. SIAM J. Imaging Sci. 3(4), 856–877 (2010)
Friedlander, M., Tseng, P.: Exact regularization of convex programs. SIAM J. Optim. 18, 4 (2007)
Lai, M.-J., Yin, W.: Augmented ℓ 1 and nuclear-norm models with a globally linearly convergent algorithm. Rice University CAAM Technical Report TR12-02 (2012)
Cai, J.-F., Candes, E., Shen, Z.: A singular value thresholding algorithm for matrix completion. SIAM J. Optim. 20(4), 2008 (1956–1982)
Hestenes, M.R.: Multiplier and gradient methods. J. Optim. Theory Appl. 4, 303–320 (1969)
Powell, M.J.D.: A method for nonlinear constraints in minimization problems. In: Fletcher, R. (ed.) Optimization, pp. 283–298. Academic Press, New York (1972)
Esser, E.: Applications of Lagrangian-based alternating direction methods and connections to split Bregman. UCLA CAM Report 09-31 (2009)
Bertsekas, D.P.: Combined primal-dual and penalty methods for constrained minimization. SIAM J. Control 13(3), 521–544 (1975)
Bertsekas, D.P.: Constrained Optimization and Lagrange Multiplier Methods. Scientific, Athena (1996)
Mosek ApS Inc.: The Mosek optimization tools, ver. 4 (2006)
Bertsekas, D.P.: Necessary and sufficient conditions for a penalty method to be exact. Math. Program. 9(1), 87–99 (1975)
Rockafellar, R.T.: Monotone operators and the proximal point algorithm. SIAM J. Control Optim. 14, 877–898 (1976)
Eckstein, J., Silva, P.J.S.: A practical relative error criterion for augmented Lagrangians. Math. Program. pp. 1–30 (2010)
Burger, M., Moller, M., Benning, M., Osher, S.: An adaptive inverse scale space method for compressed sensing. UCLA CAM Report 11-08 (2011)
Acknowledgements
The authors thank Professor Yin Zhang and two anonymous reviewers for their valuable comments.
Author information
Authors and Affiliations
Corresponding author
Additional information
Dedicated to the 70th birthday of Stanley Osher.
The authors’ work has been supported by NSF, ONR, DARPA, AFOSR, ARL and ARO.
Rights and permissions
About this article
Cite this article
Yin, W., Osher, S. Error Forgetting of Bregman Iteration. J Sci Comput 54, 684–695 (2013). https://doi.org/10.1007/s10915-012-9616-5
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10915-012-9616-5