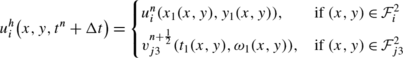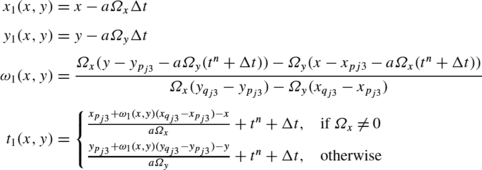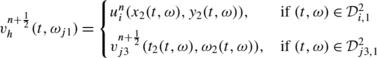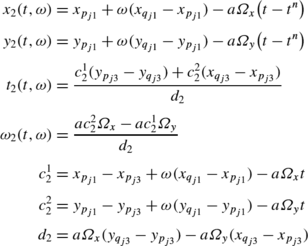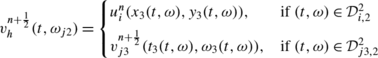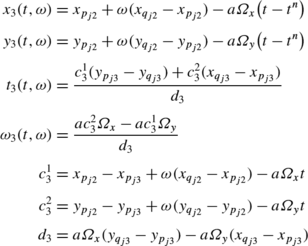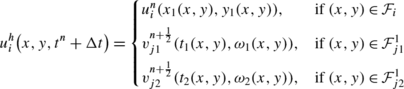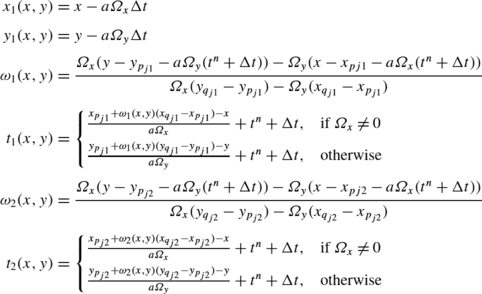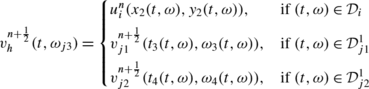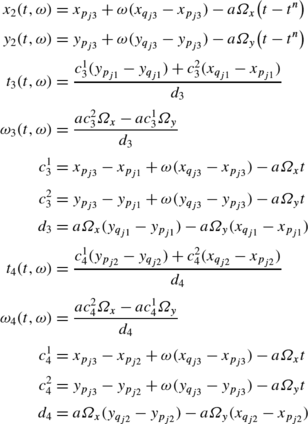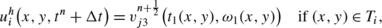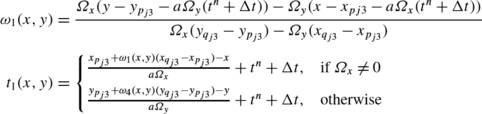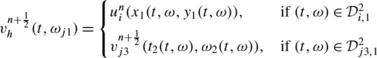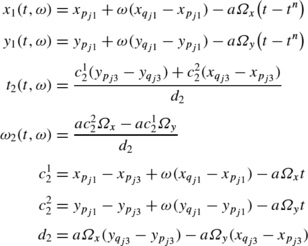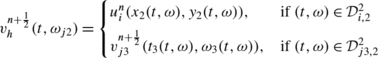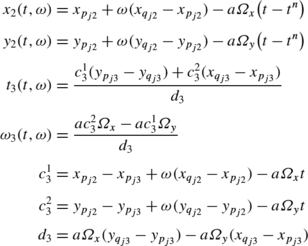Abstract
This work concerns high-order approximations of the linear advection equation in very long time. A GRP-type scheme of arbitrary high-order in space and time with no restriction on the time step is developed. In the usual GRP solvers, we consider a polynomial approximation of the solution in space in each cell at the initial time. Here, we add a second polynomial approximation of the solution in time in each interface. Thanks to this double approximation, the resulting scheme is compact. It is proved to be of order k+1 in space and time, where k is the degree of the polynomials. Thanks to the compactness of the scheme, a two-dimensional extension is detailed on unstructured meshes made of triangles. Several numerical test-cases and comparison with existing methods illustrate the excellent behaviour of the scheme.




















Similar content being viewed by others
References
Abgrall, R., Mezine, M.: Construction of second order accurate monotone and stable residual distribution schemes for unsteady flow problems. J. Comput. Phys. 188, 16–55 (2003)
Abgrall, R., Deconinck, H., Ricchiuto, M., Villedieu, N.: On uniformly high-order accurate residual distribution schemes for advection-diffusion. J. Comput. Appl. Math. 215(2), 547–556 (2008)
Abgrall, R., Larat, A., Ricchiuto, M., Tavé, C.: A simple construction of very high order non oscillatory compact schemes on unstructured meshes. Comput. Fluids 38(7), 1314–1323 (2009)
Ben-Artzi, M., Birman, A.: Application of the generalized Riemann problem method to 1-D compressible flows with material interfaces. J. Comput. Phys. 65(1), 170–178 (1986)
Ben-Artzi, M., Falcovitz, J.: Recent developments of the GRP method. JSME Int. J. Ser. B Fluids Therm. Eng. 38(4), 497–517 (1995)
Ben-Artzi, M., Falcovitz, J.: Generalized Riemann Problems in Computational Fluid Dynamics. Cambridge Monographs on Applied and Computational Mathematics. (2003)
Ben-Artzi, M., Li, J., Warnecke, G.: A direct Eulerian GRP scheme for compressible fluid flows. J. Comput. Phys. 218, 19–43 (2006)
Berthon, C., Turpault, R.: Asymptotic preserving HLL schemes. Numer. Methods Partial Differ. Equ. 27(6), 1396–1422 (2011)
Chalons, C., Coquel, F., Godlewski, E., Raviart, P.A., Seguin, N.: Godunov-type schemes for hyperbolic systems with parameter dependent source. The case of Euler system with friction. Math. Models Methods Appl. Sci. 20(11), 2109 (2010)
Chandrasekhar, S.: Radiative Transfer. Dover, New York (1950)
Cockburn, B., Shu, C.W.: TVD Runge-Kutta local projection discontinuous Galerkin finite element method for scalar conservation laws II: general framework. Math. Comput. 52, 411 (1989)
Cockburn, B., Shu, C.W.: The Runge-Kutta discontinuous Galerkin method for conservation laws V: multidimensional systems. J. Comput. Phys. 141(2), 199–224 (1998)
Dai, W.W., Woodward, P.R.: Moment preserving schemes for Euler equations. Comput. Fluids 46, 186–196 (2011)
Davidson, B.: Neutron Transport Theory. Clarendon, Oxford (1957)
Degond, P., Pareschi, L., Russo, G.: Modeling and Computational Methods for Kinetic Equations. Birkhäuser, Basel (2004)
Dumbser, M., Käser, M.: Arbitrary high order non-oscillatory finite volume schemes on unstructured meshes for linear hyperbolic systems. J. Comput. Phys. 221(2), 693–723 (2007)
Dumbser, M., Munz, C.D.: Arbitrary high-order discontinuous Galerkin schemes. In: Numerical Methods for Hyperbolic and Kinetic Problems, pp. 295–333 (2005)
Dumbser, M., Zanotti, O.: Very high order PNPM schemes on unstructured meshes for the resistive relativistic MHD equations. J. Comput. Phys. 228(18), 6991–7006 (2009)
Dumbser, M., Balsara, D., Munz, C.D., Toro, E.F.: A unified framework for the construction of one-step finite-volume and discontinuous Galerkin schemes on unstructured meshes. J. Comput. Phys. 227(18), 8209–8253 (2008)
Dumbser, M., Enaux, C., Toro, E.F.: Finite volume schemes of very high order of accuracy for Stiff hyperbolic balance laws. J. Comput. Phys. 227(8), 3971–4001 (2008)
Filbet, F., Jin, S.: An asymptotic preserving scheme for the ES-BGK model of the Boltzmann equation. J. Sci. Comput. 46, 204–224 (2011)
Frénod, E., Salvarani, F., Sonnendrücker, E.: Long time simulation of a beam in a periodic focusing channel via a two-scale PIC-method. Math. Models Methods Appl. Sci. 19(2), 175–197 (2009)
Gassner, G., Dumbser, M., Hindenlang, F., Munz, C.D.: Explicit one-step time discretizations for discontinuous Galerkin and finite volume schemes based on local predictors. J. Comput. Phys. 230, 4232–4247 (2011)
Glassey, R.T.: The Cauchy Problem in Kinetic Theory. SIAM, Philadelphia (1996)
Glimm, J., Marshall, G., Plohr, B.: A generalized Riemann problem for quasi-one-dimensional gas flows. Adv. Appl. Math. 5(1), 1–30 (1984)
Gosse, L., Toscani, G.: Asymptotic-preserving & well-balanced schemes for radiative transfer and the Rosseland approximation. Numer. Math. 98, 223–250 (2003)
Gottlieb, S., Shu, C.W.: Total variation diminishing Runge-Kutta schemes. Math. Comput. 67, 73–85 (1998)
Harten, A., Engquist, B., Osher, S., Chakravarthy, S.R.: Uniformly high-order accurate essentially non-oscillatory schemes, III. J. Comput. Phys. 71(2), 231–303 (1987)
Helffer, B., Nier, F.: Hypoelliptic Estimates and Spectral Theory for Fokker-Planck Operators and Witten Laplacians. Springer, Berlin (2005)
Hoteit, H., Ackerer, P., Mosé, R., Erhel, J., Philippe, B.: New two-dimensional slope limiters for discontinuous Galerkin methods on arbitrary meshes. Int. J. Numer. Methods Eng. 61(14), 2566–2593 (2004)
Jiang, G.S., Shu, C.W.: Efficient implementation of weighted ENO schemes. J. Comput. Phys. 126(1), 202–228 (1996)
Jin, S.: Efficient asymptotic-preserving (AP) schemes for some multiscale kinetic equations. SIAM J. Sci. Comput. 21, 441–454 (1999)
Klaij, C., van der Vegt, J.J.W., van der Ven, H.: Space-time discontinuous Galerkin method for the compressible Navier-Stokes equations. J. Comput. Phys. 217, 589–611 (2006)
Lemou, M., Mieussens, L.: Time implicit schemes and fast approximations of the Fokker-Planck-Landau equation. SIAM J. Sci. Comput. 27(3), 809–830 (2007)
LeVeque, R.J.: Finite Volume Methods for Hyperbolic Problems. Cambridge University Press, Cambridge (2002)
Liu, T.P., Osher, S., Chan, T.: Weighted essentially non-oscillatory schemes. J. Comput. Phys. 115, 200–212 (1994)
Lörcher, F., Gassner, G., Munz, C.D.: A discontinuous Galerkin scheme based on a space-time expansion. I. Inviscid compressible flow in one space dimension. J. Sci. Comput. 32(2), 175–199 (2007)
Lowrie, R.B., Roe, P.L., Van Leer, B.: A space-time discontinuous Galerkin method for the time accurate numerical solution of hyperbolic conservation laws. In: Proceedings of 12th AIAA CFD Conference, pp. 95–1658 (1995)
Mihalas, D., Weibel-Mihalas, B.: Foundations of Radiation Hydrodynamics. Dover, New York (1999)
Pomraning, G.C.: The Equations of Radiation Hydrodynamics. Pergamon, Elmsford (1973)
Toro, E.F.: Riemann Solvers and Numerical Methods for Fluid Dynamics. A Practical Introduction. Springer, Berlin (1999)
van der Vegt, J.J.W., van der Ven, H.: Space-time discontinuous Galerkin finite element method with dynamic grid motion for inviscid compressible flows I. General formulation. J. Comput. Phys. 182, 546–585 (2002)
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
Evolution Step
Case two targets (explicit):
-
∘
We know the solution \(u_{i}^{n}(x,y)\) in the cell T i at time t n and the solution \(v_{j3}^{n+\frac{1}{2}}(t,\omega)\) on the interface \(I_{j3}^{n+\frac{1}{2}}\) .
-
∘
We define θ 1 as the intersection between the characteristic line coming from \(s_{j3}^{n}\) and the segment \(s_{j1}^{n+1}\). We also define θ 2, the intersection between the characteristic line coming from \(s_{j3}^{n}\) and the segment \(s_{j2}^{n+1}\). Then we call M 1 the projection of θ 1 on \(s_{j1}^{n}\) and M 2 the projection of θ 2 on \(s_{j2}^{n}\) (see Fig. 21).
-
∘
The exact solution on the cell T i at time t n+1 is:
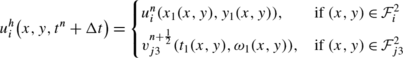
with:
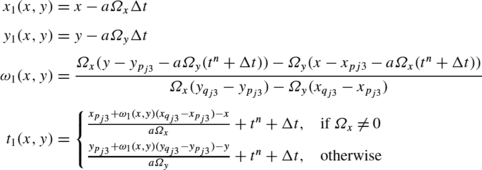
-
∘
The exact solution on the interface \(I_{j1}^{n+\frac{1}{2}}\) is:
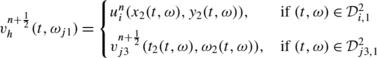
with:
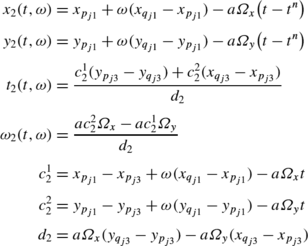
-
∘
The exact solution on the interface \(I_{j2}^{n+\frac{1}{2}}\) is:
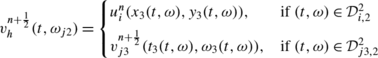
with:
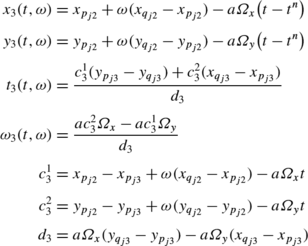
Case one target (explicit):
-
∘
We know the solution \(u_{i}^{n}(x,y)\) in the cell T i at time t n and the solutions \(v_{j1}^{n+\frac{1}{2}}(t,\omega)\) and \(v_{j2}^{n+\frac{1}{2}}(t,\omega)\) on the interfaces I j1 and \(I_{j2}^{n+\frac{1}{2}}\).
-
∘
We define θ 1 as the intersection between the characteristic line coming from the segment \(s_{j1}^{n}\) and the segment \(s_{j3}^{n+1}\) (i.e. such that \(d(s_{j3}^{n},s_{j1}^{n}) = a \Delta t\)). We also define θ 2 as the intersection between the characteristic line coming from the segment \(s_{j2}^{n}\) and the segment \(s_{j3}^{n+1}\) (i.e. such that \(d(s_{j3}^{n},s_{j2}^{n}) = a \Delta t\)). Then we call M 1 the projection of θ 1 on \(s_{j3}^{n}\) and M 2 the projection of θ 2 on \(s_{j3}^{n}\) (see Fig. 22).
-
∘
The exact solution on the cell T i at time t n+1 is:
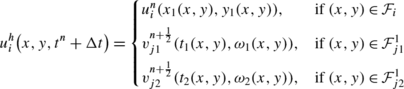
with:
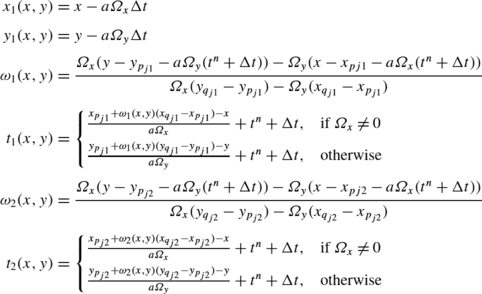
-
∘
The exact solution on the interface \(I_{j3}^{n+\frac{1}{2}}\) is:
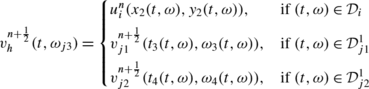
with:
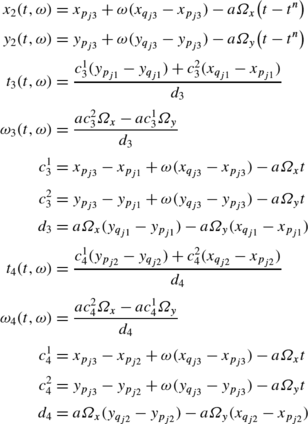
Case two targets (implicit):
-
∘
We know the solution \(u_{i}^{n}(x,y)\) in the cell T i at time t n and the solution \(v_{j3}^{n+\frac{1}{2}}(t,\omega)\) on the interface \(I_{j3}^{n+\frac{1}{2}}\) .
-
∘
We define θ 3 as the intersection between the characteristic line coming from \(s_{j3}^{n}\) and the segment [t n,t n+1] for (x,y)=(x j3,y j3) (see Fig. 23).
-
∘
The exact solution on the cell T i at time t n+1 is:
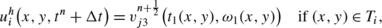
with:
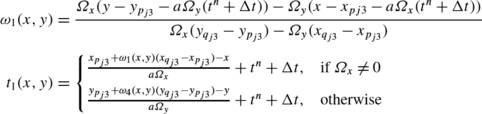
-
∘
The exact solution on the interface \(I_{j1}^{n+\frac{1}{2}}\) is:
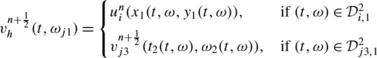
with:
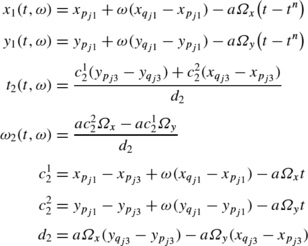
-
∘
The exact solution on the interface \(I_{j2}^{n+\frac{1}{2}}\) is:
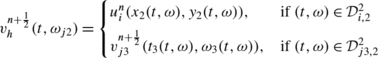
with:
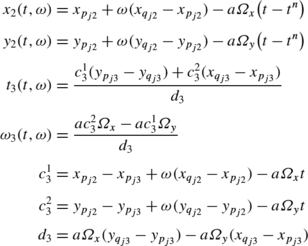
Projection Step
The exact solutions are respectively projected onto the spaces \(\mathbb {P}^{k}_{C}\) and \(\mathbb {P}^{k}_{I}\): in the cell T i at time t n+1, the exact solution is projected in \(\mathbb {P}^{k}_{C}\), and on the interfaces \(I_{j}^{n+\frac{1}{2}}\), the solution is projected in \(\mathbb {P}^{k}_{I}\). For the case n∘1 explicit, this leads to the two minimization problems:


for the case n∘2 explicit, it leads to the three minimization problems:



and for the case explicit two targets, it also leads to three minimization problems:



Thanks to the Petrov-Galerkin conditions, we can rewrite (20), (21) as:





Using the decomposition of the solutions in their corresponding basis:

the minimization problems (28), (29) are equivalent to solving the two following linear systems of size \(\frac{(k+1)(k+2)}{2}\):

and (30)–(32) are equivalent to solving three linear systems of size \(\frac{(k+1)(k+2)}{2}\):

The matrices are the same that in the case n∘1 implicit and the case n∘2 explicit. For the right hand sides, we have first for the case n∘1 explicit:

then for the case n∘2 implicit:

and for the case explicit two targets:

where the coefficients are given by:

Rights and permissions
About this article
Cite this article
Berthon, C., Sarazin, C. & Turpault, R. Space-time Generalized Riemann Problem Solvers of Order k for Linear Advection with Unrestricted Time Step. J Sci Comput 55, 268–308 (2013). https://doi.org/10.1007/s10915-012-9632-5
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10915-012-9632-5