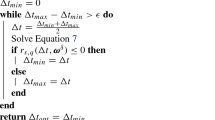Skip to main content
SpringerLink
Log in

Matrix-Free Polynomial-Based Nonlinear Least Squares Optimized Preconditioning and Its Application to Discontinuous Galerkin Discretizations of the Euler Equations

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

Abstract

We introduce a preconditioner that can be both constructed and applied using only the ability to apply the underlying operator. Such a preconditioner can be very attractive in scenarios where one has a highly efficient parallel code for applying the operator. Our method constructs a polynomial preconditioner using a nonlinear least squares (NLLS) algorithm. We show that this polynomial-based NLLS-optimized (PBNO) preconditioner significantly improves the performance of a discontinuous Galerkin (DG) compressible Euler equation model when run in an implicit–explicit time integration mode; note that IMEX methods are valuable only for low Mach number flows. The PBNO preconditioner achieves significant reduction in GMRES iteration counts and model wall-clock time, and significantly outperforms several existing types of generalized (linear) least squares polynomial preconditioners. Comparisons of the ability of the PBNO preconditioner to improve DG model performance when employing the Stabilized Biconjugate Gradient algorithm (BICGS) and the basic Richardson iteration are also included. In particular, we show that higher order PBNO preconditioning of the Richardson iteration (run in a dot product free mode) makes the algorithm competitive with GMRES and BICGS in a serial computing environment. Because the NLLS-based algorithm used to construct the PBNO preconditioner can handle both positive definite and complex spectra without any need for algorithm modification, we suggest that the PBNO preconditioner is, for certain types of problems, an attractive alternative to existing polynomial preconditioners based on linear least-squares methods.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12

Similar content being viewed by others

Notes

  1. In [16] it was shown that deriving the DG Schur-complement form for general boundary conditions remains an open problem.

  2. The DG-IMEX model used in this paper is a mature model that has already been presented in a series of papers in the literature. For this reason we do not show either spatial or temporal convergence rates since these have already been presented previously. E.g., see [5, 7, 12, 13] for the verification of the DG method and [9] for convergence rates of the IMEX time-integrators.

  3. The reason the matrix remains constant with time is due to some judicious choices we make. First, we linearize the nonlinear system about a spatially dependent, but time-independent basic state. Next, in our IMEX-RK approach we only use SDIRK methods which, in the Butcher tableau, have constant diagonal terms (see [9]).

  4. See Sect. 4.1 for the details of how \(\tilde{H}\) is constructed.

  5. For all cases in this paper we use \(\varvec{c}_0 = [1 \ldots 1]^T\), which, by virtue of the form of Eq. (17), makes \(s_L(\lambda )=1\).

  6. The range of iteration values just cited excludes the case when \(p=2\) and the spectrum of \(\tilde{A}\) is positive definite, in which case optimization problem (23) is linear and GN converges in a single step.

  7. Recall that in NUMA neither the unscaled system matrix A nor the scaled system matrix \(\tilde{A}\) is ever constructed.

  8. NUMA2D refers to the two-dimensional version of the NUMA model.

  9. A Courant No. of 32 is the largest for which the RTB problem will run to completion (i.e., bubble at top of domain at 700 s) without exceeding the CFL limit of the explicit part of the IMEX method.

  10. By making the polynomial order the largest we consider in this paper (i.e., 9th-order) we maximize the number of Gauss–Newton iterations required during the construction of the preconditioner, and thus maximize the construction cost.

  11. The total number of grid points in this simulation is 50,625 with each grid point having four variables for a total of 202,500 degrees of freedom. Using a time-step of \(\hbox {dt}=0.148287\) means that the linear system has to be solved \(\frac{700 \cdot k}{dt}=18{,}882\) times during the 700 s simulation, where k = 4 denotes the number of implicit Runge–Kutta stages used in the ARK method.

  12. We emphasize here that the use of artificial viscosity is not necessary for NUMA2D-DG to run the discontinuous RTB case to completion, and has no effect on the performance of the PBNO preconditioner. Rather the numerical viscosity has been added solely for the purpose of avoiding the generation of spurious eddies associated with imposing a curving discontinuous initial condition on a rectangularly discretized model domain, and thus allowing the continuous and discontinuous runs to produce visually comparable results.

References

  1. Benzi, M.: Preconditioning techniques for large linear systems: a survey. J. Comput. Phys. 182, 418–477 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  2. Benzi, M., Tuma, M.: A sparse approximate inverse preconditioner for nonsymmetric linear systems. SIAM J. Sci. Comput. 19, 968–994 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  3. Carr III, L.E., Borges, C.F., Giraldo, F.X.: An element-based spectrally-optimized approximate inverse preconditioner for the Euler equations. SIAM J. Sci. Comput. 34, B392–420 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  4. Dubois, P.F., Greenbaum, A., Rodrigue, G.H.: Approximating the inverse of a matrix for use in iterative algorithms on vector processors. Computing 22, 257–268 (1979)

    Article  MathSciNet  MATH  Google Scholar 

  5. Escobar-Vargas, J.A., Diamessis, P.J., Giraldo, F.X.: High-order discontinuous element-based schemes for the inviscid shallow water equations: spectral multidomain penalty and discontinuous Galerkin methods. Appl. Math. Comput. 218, 4825–4848 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  6. van Gijzen, M.B.: A polynomial preconditioner for the GMRES algorithm. J. Comput. Appl. Math. 59, 9197 (1995)

    Google Scholar 

  7. Giraldo, F.X., Restelli, M.: A study of spectral element and discontinuous Galerkin methods for the Navier–Stokes equations in nonhydrostatic mesoscale atmospheric modeling: equation sets and test cases. J. Comput. Phys. 227, 3849–3877 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  8. Giraldo, F.X., Restelli, M., Lauter, M.: Semi-implicit formulations of the Navier-Stokes equations: applications to nonhydrostatic atmospheric modeling. SIAM J. Sci. Comput. 32, 3394–3425 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  9. Giraldo, F.X., Kelly, J.F., Constantinescu, E.M.: Implicit-explicit formulations for a 3D nonhydrostatic unified model of the atmospheric (NUMA). SIAM J. Sci. Comput. 35, B1162–1194 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  10. Kelly, J.F., Giraldo, F.X.: Continuous and discontinuous galerkin methods for a scalable 3D nonhydrostatic atmospheric model: limited area mode. J. Comput. Phys. 231, 7988–8008 (2012)

  11. Kennedy, C., Carpenter, M.: Additive Runge–Kutta schemes for convection-diffusion-reaction equations. Appl. Numer. Math. 44, 139–181 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  12. Kopera, M.A., Giraldo, F.X.: Analysis of adaptive mesh refinement for IMEX discontinuous Galerkin solutions of the compressible euler equations with application to atmospheric simulations. J. Comput. Phys. 275, 92–117 (2014)

    Article  MathSciNet  Google Scholar 

  13. Kopera, M.A., Giraldo, F.X.: Mass conservation of unified continuous and discontinuous element-based galerkin methods on dynamically adaptive grids with application to atmospheric simulations. J. Comput. Phys. (accepted, May 2015)

  14. Liang, Y.: Generalized least-squares polynomial preconditioners for symmetric indefinite linear equations. Parallel Comput. 28, 323–341 (2002)

    Article  MathSciNet  Google Scholar 

  15. Liang, Y.: The Use of Parallel Polynomial Preconditioners in the Solution of Systems of Linear Equations. Ph.D. dissertation, University of Ulster (2005)

  16. Restelli, M., Giraldo, F.X.: A conservative semi-implicit discontinuous galerkin method for the Navier–Stokes equations in nonhydrostatic mesoscale atmospheric modeling. SIAM J. Sci. Comput. 31, 2231–2257 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  17. Saad, Y.: Iterative solution of indefinite symmetric linear systems by methods using orthogonal polynomials over two disjoint intervals. SIAM J. Numer. Anal. 20, 784–811 (1983)

    Article  MathSciNet  MATH  Google Scholar 

  18. Saad, Y.: Least squares polynomials in the complex plane and their use for solving nonsymmetric linear systems. SIAM J. Numer. Anal. 24, 155–169 (1987)

    Article  MathSciNet  MATH  Google Scholar 

  19. Saad, Y.: Iterative Methods for Sparse Linear Systems. SIAM, Philadelphia (2003)

    Book  MATH  Google Scholar 

  20. Saad, Y., Schultz, M.H.: GMRES: a generalized minimal residual algorithm for solving nonsymmetric linear systems. SIAM J. Sci. Stat. Comput. 7, 856–869 (1986)

    Article  MathSciNet  MATH  Google Scholar 

  21. Trefethen, L.N., Bau III, D.: Numerical Linear Algebra. SIAM, Philadelphia (1997)

    Book  MATH  Google Scholar 

  22. van der Vorst, H.A.: Bi-CGSTAB: a fast and smoothly converging variant of Bi-CG for the solution of nonsymmetric linear systems. SIAM J. Sci. Stat. Comput. 13, 631–644 (1992)

    Article  MATH  Google Scholar 

  23. van der Vorst, H.A.: Iterative Krylov Methods for Large Linear Systems. Cambridge University Press, New York (2003)

    Book  MATH  Google Scholar 

Download references

Acknowledgments

The authors gratefully acknowledge the support of the Computational Mathematics program of the Air Force Office of Scientific Research, the Office of Naval Research through program element PE-0602435N, and the National Science Foundation (Division of Mathematical Sciences) through program element 121670. We also would like to thank Michal Kopera and several anonymous reviewers for their helpful suggestions for improving the manuscript.

Conflict of interest

The authors declare that they have no conflict of interest.

Author information

Authors and Affiliations

  1. Department of Applied Mathematics, Naval Postgraduate School, Monterey, CA, 93943, USA

    L. E. Carr III, C. F. Borges & F. X. Giraldo

Authors
  1. L. E. Carr III
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. C. F. Borges
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. F. X. Giraldo
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to F. X. Giraldo.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Carr, L.E., Borges, C.F. & Giraldo, F.X. Matrix-Free Polynomial-Based Nonlinear Least Squares Optimized Preconditioning and Its Application to Discontinuous Galerkin Discretizations of the Euler Equations. J Sci Comput 66, 917–940 (2016). https://doi.org/10.1007/s10915-015-0049-9

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10915-015-0049-9

Keywords

Mathematics Subject Classification

Search

Navigation